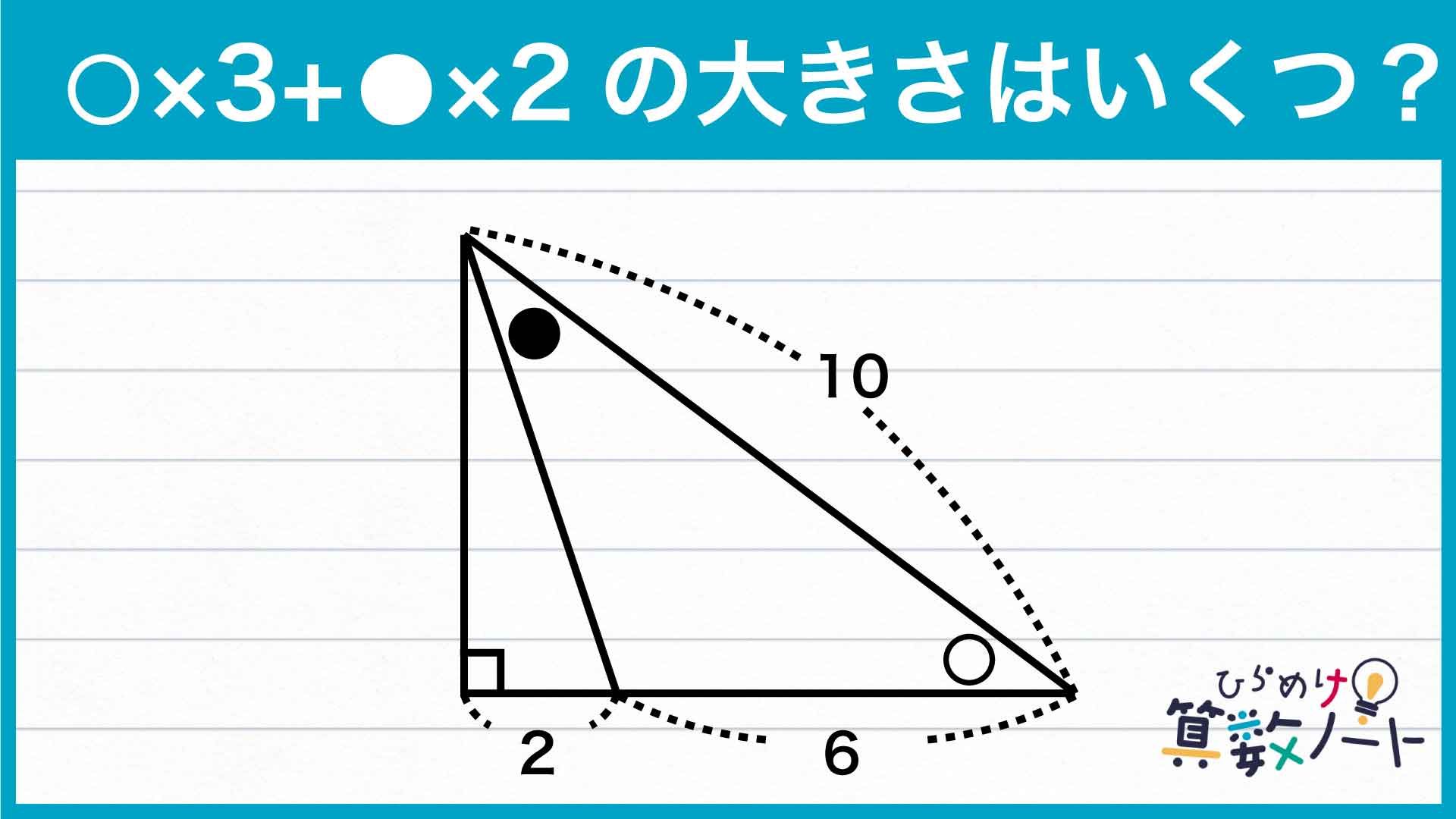
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
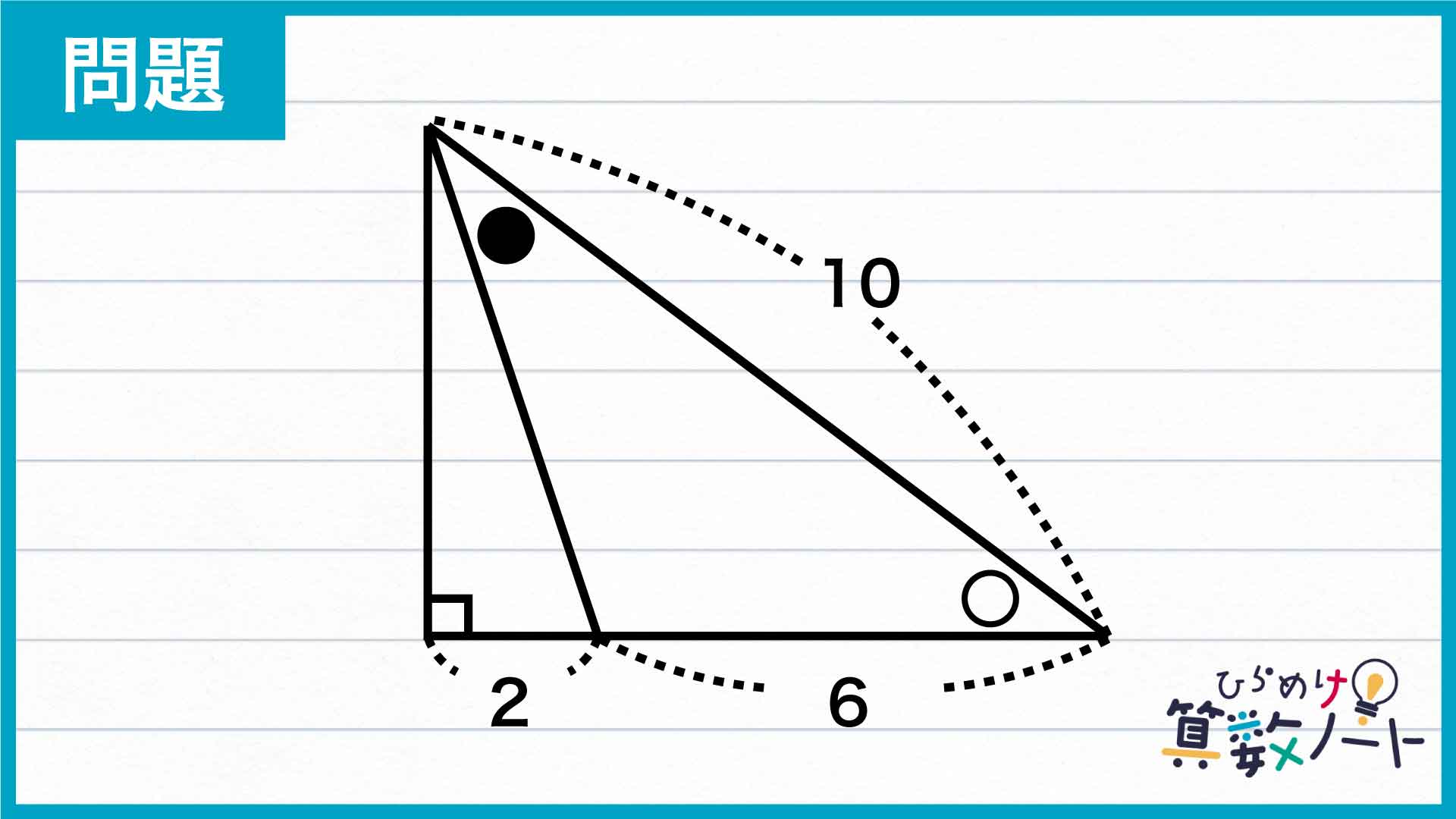
この問題の解き方をまとめた図がこちらです。
ポイントは、三角形を書き足して二等辺三角形を作り、大きさの等しい角を見つけていくことです。
では、このポイントを踏まえつつ解いていきましょう!
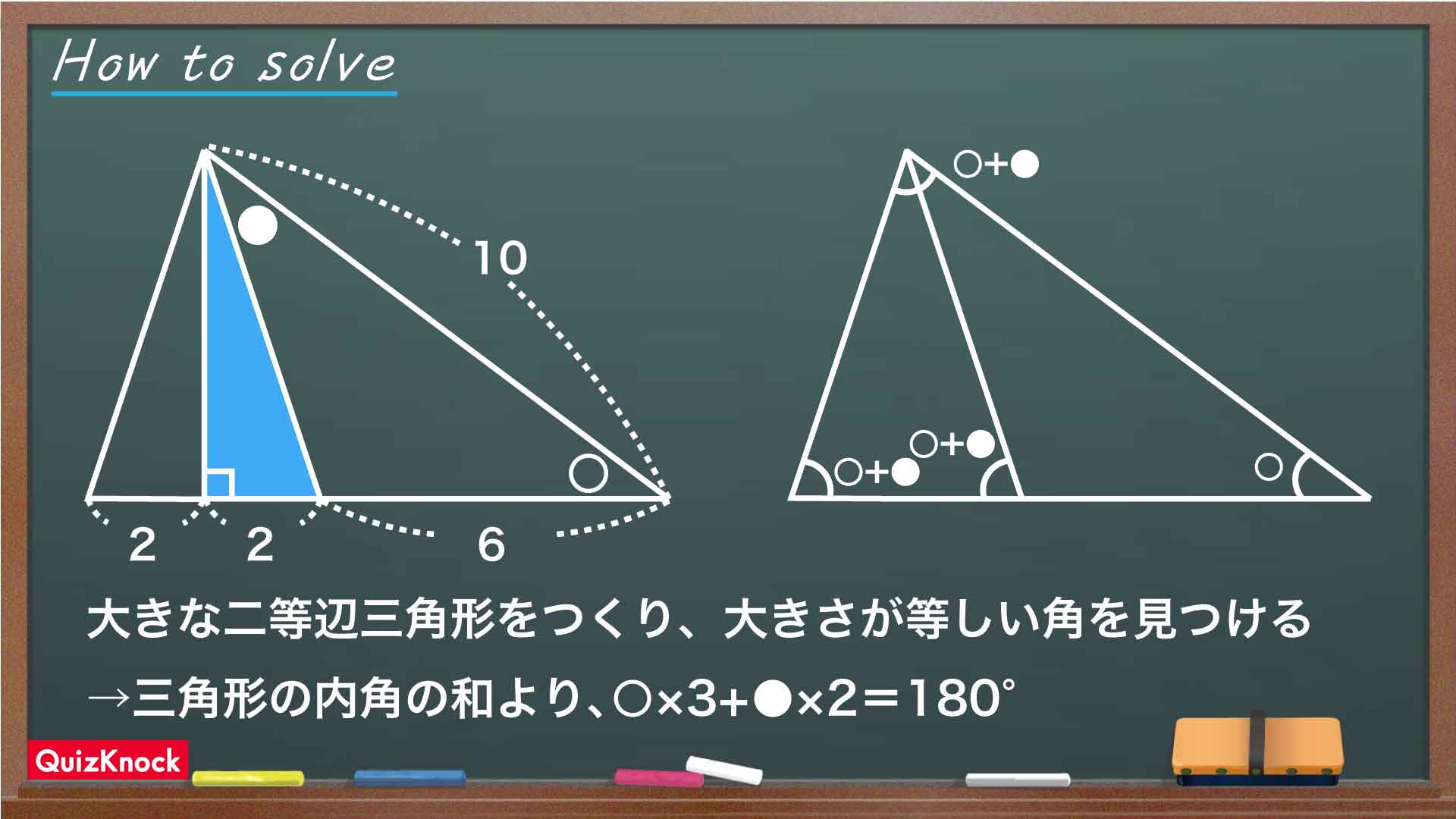
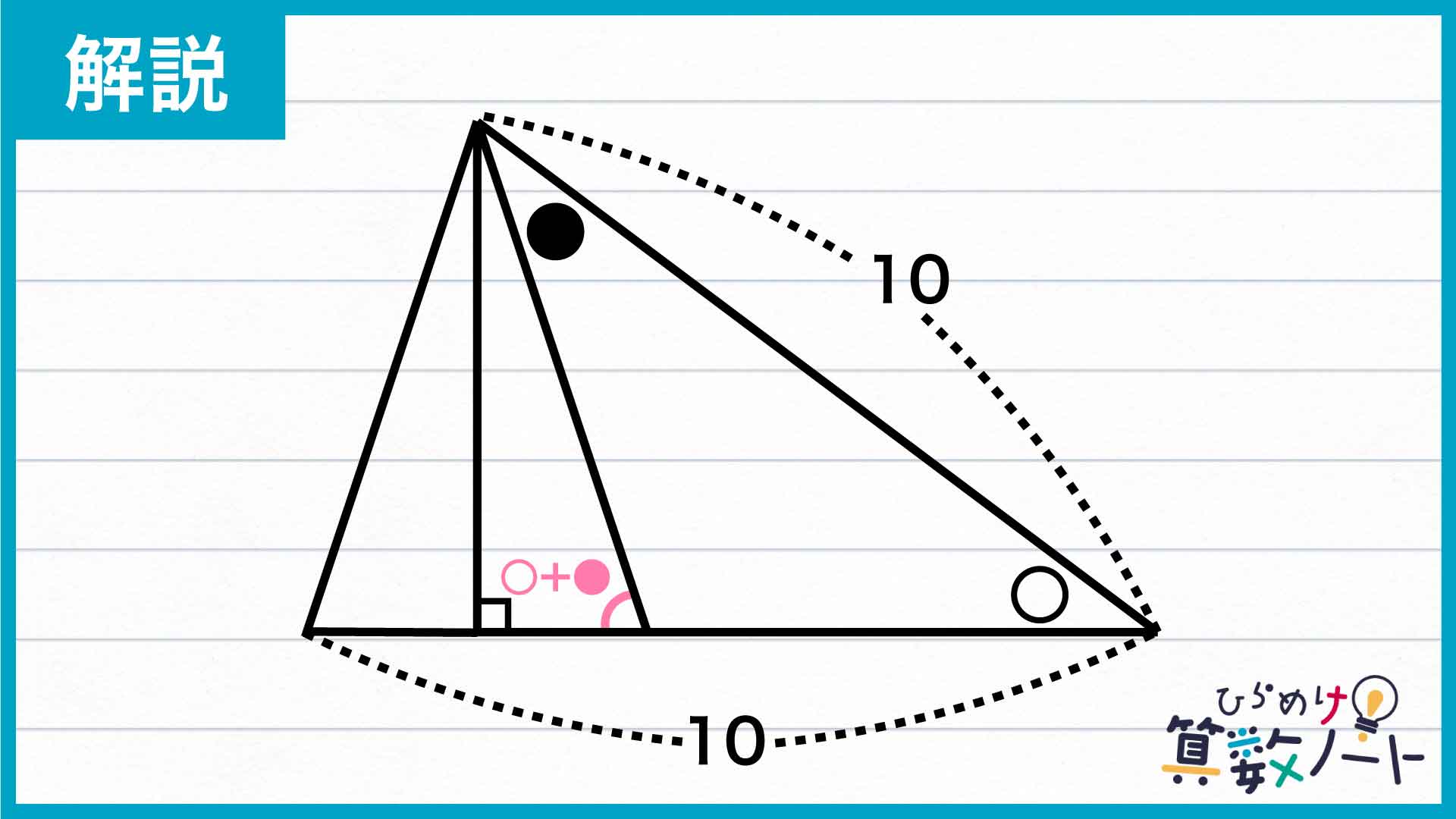
三角形を書き足す
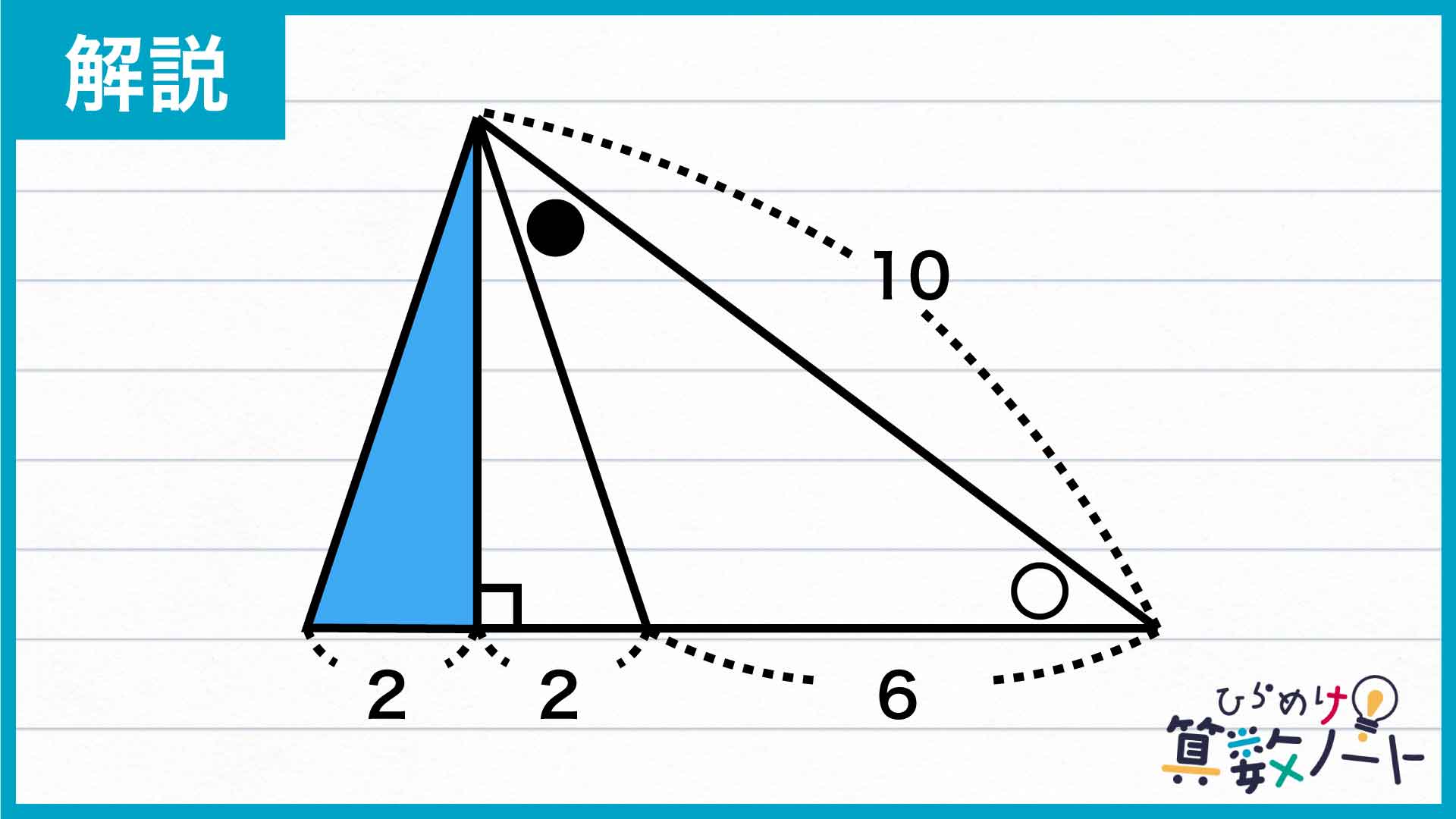
まず注目すべきは、大きな直角三角形を区切ってできた左側の小さな直角三角形です。この直角三角形を、反転させた上で左にもう1つくっつけてみましょう。
新しくできた大きな三角形の辺の長さに注目します。2+2+6=10より、〇の角を挟んで向かい合った2辺はともに長さが10で等しくなっています。したがって、この三角形は二等辺三角形であることがわかるのです。
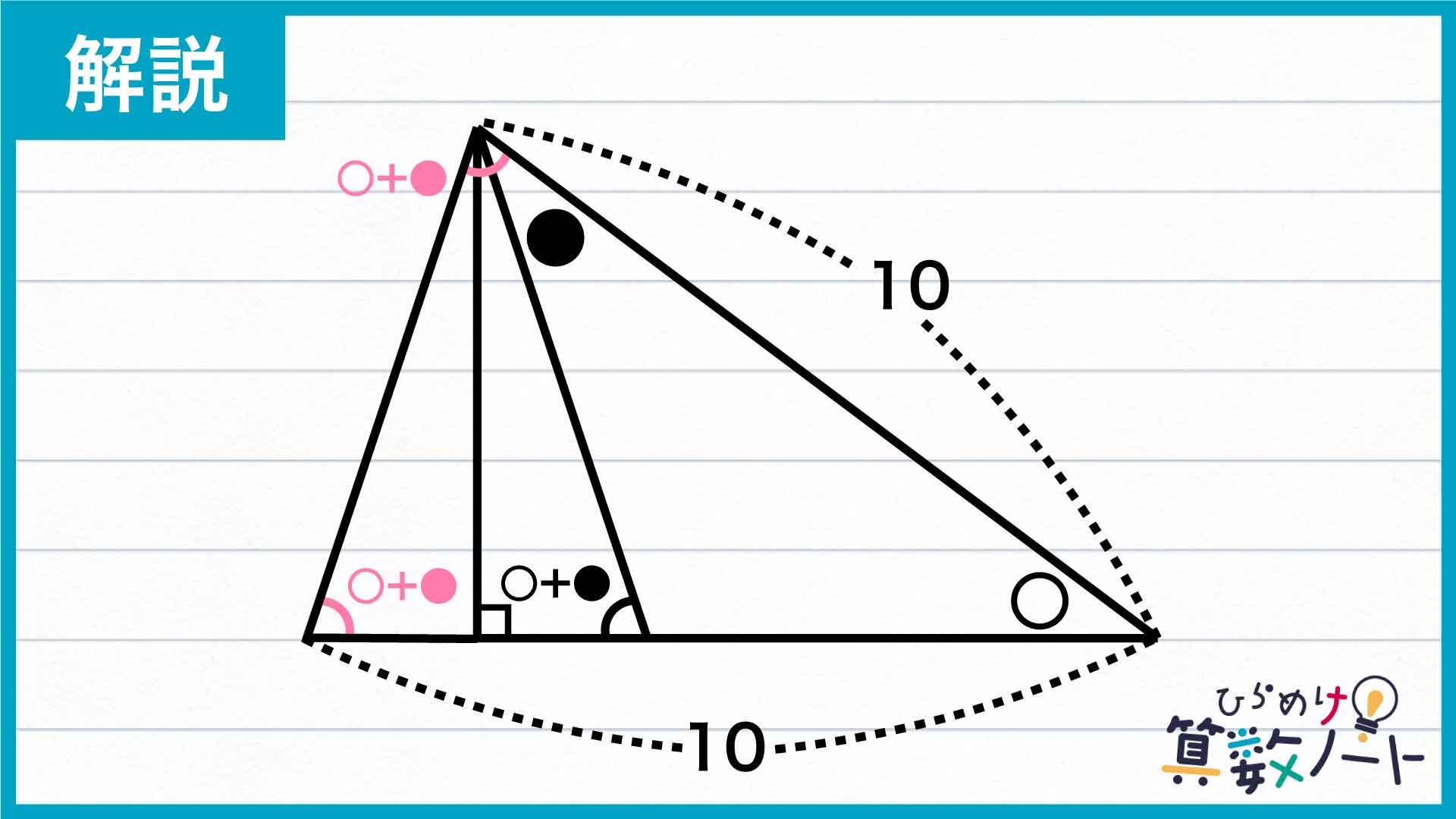
〇と●で角の大きさを表す
三角形の外角の大きさは、隣り合っていない2つの内角の和と等しくなります。したがって、下の図に示された角の大きさは〇+●と表すことができます。
左側にくっついた三角形は元からあった小さな直角三角形と同じものなので、左端の角の大きさも同じく〇+●です。さらに、大きな三角形が二等辺三角形であることから上にも大きさの等しい角が存在します。以上を踏まえて、下の図のように大きさの等しい角を3つ見つけることができました。
三角形の内角の和が必ず180度になることから、大きな三角形の内角に注目すると〇+(〇+●)+(〇+●)=〇×3+●×2=180度が成り立ちます。したがって、求める〇×3+●×2の値は180度であることがわかるのです。
答え:180度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】