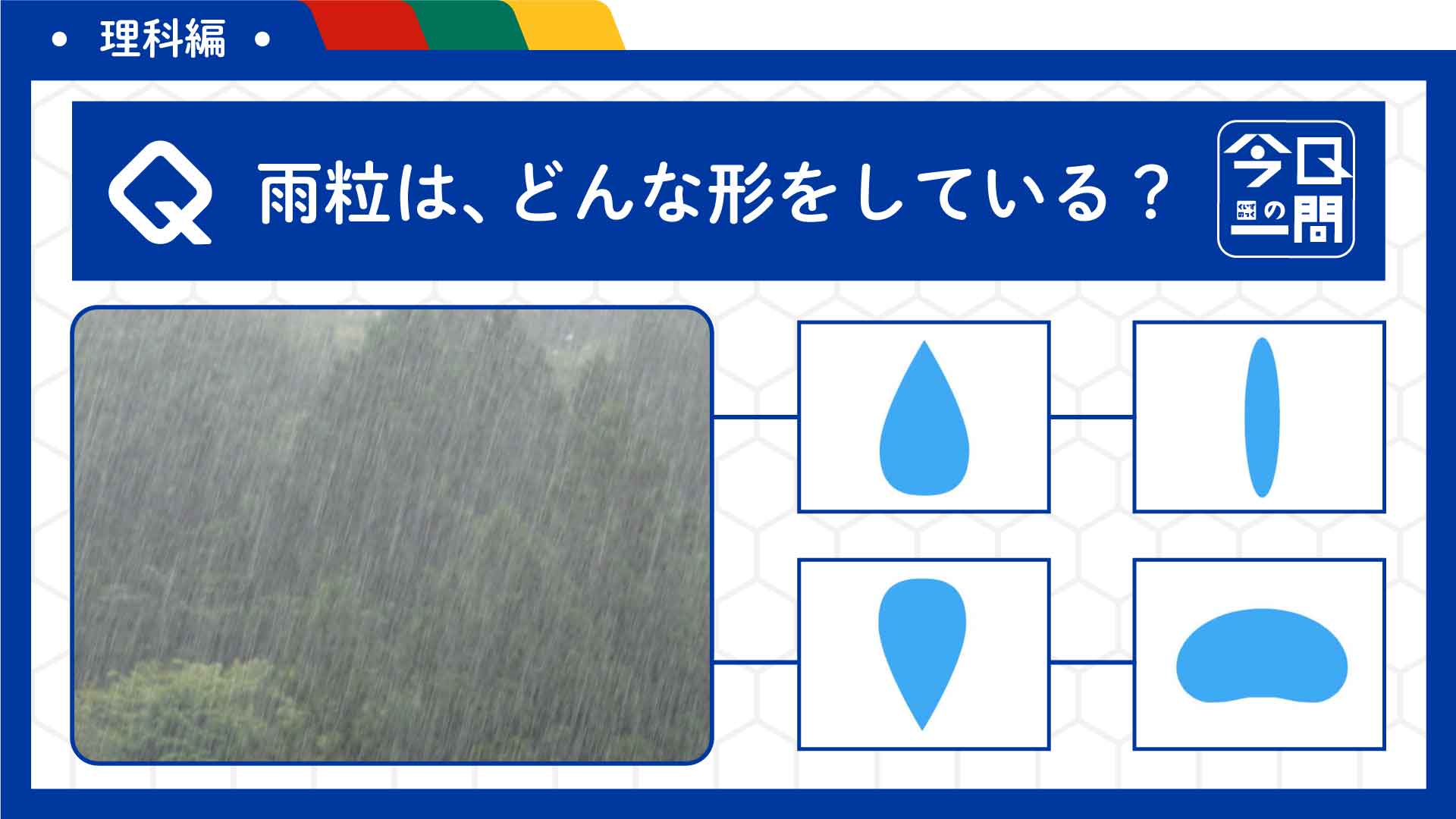
あけましておめでとうございます。
ついに2017年ですね!!
2017といえば?
そう、素数。
2011年以来6年ぶりの素数年で、この次は2027年まで訪れません。
この素数フィーバー、騒がない訳にはいかないでしょう!!
さて、タイトルの□に当てはまる数字は何か、分かりましたか?
これはメルセンヌ数である素数、メルセンヌ素数を書き並べたものです。
メルセンヌ数列は1,3,7,15,31,63,127,…という数列です。
1を足すと2,4,8,16,32,64,128,…となりますよね。
実は、2n-1と表される数字をメルセンヌ数というのです。
このうち素数であるものをメルセンヌ素数と呼んでいます。
つまり答えは7でした。
実は昨年、過去最大の素数が発見されましたが、これはメルセンヌ素数でした。
というのも、リュカ・レーマー・テストという判定法があるためメルセンヌ数は普通の数と比べて素数か合成数かを判定するのが簡単です。
(合成数とは、約数が3つ以上ある数のことで、簡単に言えば「素数じゃない方」。ただし、1は素数でも合成数でもない。)
そのため、巨大な素数を発見するにはメルセンヌ数を調べていくのが手っ取り早いのです。
今回見つかった素数、どれくらい大きいと思います?
なんと、274207281-1という2233万8618桁の数字なんです!
2200万桁……逆にピンと来ないですね。
ためしに400字詰め原稿用紙に書き写すとしましょう。1文字書き写すのに2秒かかるとすると全部で517日間かかります。紙の枚数は5万枚以上! 重さは7.5トン以上になります!
ちなみに新しいメルセンヌ素数を発見すると3000ドル、初めて1億桁を越えるメルセンヌ素数を発見すると5万ドルの懸賞金がもらえます。
さぁ、最大の素数の発見と記念すべき西暦2017年を祝して、素数限定の数列クイズを作りました。
素数に関する知識で解くか? 並びの法則にひらめくか? □に入る数字を当ててください!










.jpg)