ストレートよりもカーブを打つほうが得意。ナイスガイの須貝です。
皆さんは火の玉ストレートという言葉を聞いたことがありますか?
阪神タイガースの藤川球児選手が投げる、ホップアップするようなストレートがよく「火の玉」と形容されます。唸るような豪速球、しかも浮き上がって見えるような「魔球」は「火の玉」と呼ぶにふさわしいものだと思います。
ところで、僕は考えました。
「本当に燃え上がる魔球を投げたら最強になれるんじゃないか?」
その燃える魔球、文字通りの火の玉ストレートの圧力を前にした打者は為す術なく見逃し三振をしてしまうことでしょう。
断熱圧縮
では、燃える魔球を発生させうるとしたら、どのような原理を使えば良いのでしょうか?
速いものが空気中を飛来し、炎上する、といえば隕石ですね。
隕石が燃え上がるのは、空気を急激に押しつぶしたことによる「断熱圧縮」が原因。
隕石の表面温度があがり、鉄や岩石が真っ赤にとけて光っていることによります。その速度は時速数万kmから数十万kmで、温度も数万度に達するそうです。
押しつぶすといっても、例えば普通のピストンで空気をつぶしてもピストンの壁から熱が逃げてしまい、結果として空気の温度は上がりません。しかし、断熱することで、すなわち、周りに熱を逃さないことで温度が上がるのです。
隕石は猛スピードで空気に突っ込んでいるので、熱が逃げるよりも空気を押しつぶして温度が上がる効果のほうが早いために火の玉になっています。
空気との摩擦で燃え上がるようにも思えますが、実はその効果より、空気を押しつぶしたことによる温度上昇の効果のほうが大きいのです。
革の発火点
さて、野球ボールを燃え上がらせたい。
野球のボールは革でできていて、その発火点はおよそ 500 ℃ です。 500 ℃ は絶対温度に直せば 773 K(ケルビン)です。
(絶対温度というのはそれ以下にできないこの世の最低温度 = -273 ℃を0度とした温度の基準で単位はK(ケルビン)を用います。)
ボールの温度を空気の圧縮によって773 Kまで上昇させればよいということですね。少し言い換えれば、ボールに触れている空気の温度を圧縮によって773 Kまで上昇させる、というのが今回の目的です。
隕石のような猛スピードで投げれば熱が逃げるより早く押しつぶすことも可能なのでしょうが、僕が投げられるのはせいぜい 120 km/h です。藤川投手でも 150 km/h であることを考えれば、隕石のスピードには遥か及びません。スピードだけを再現するのは現実的ではないでしょう。
ところが今回のキーワードは「断熱圧縮」です。断熱の部分を達成できれば速度は必要ありません!
ポアソンの法則
※以下数段落、読み飛ばし可
ポアソンの法則によれば、周りに熱が逃げないようにした気体の温度と体積の間には
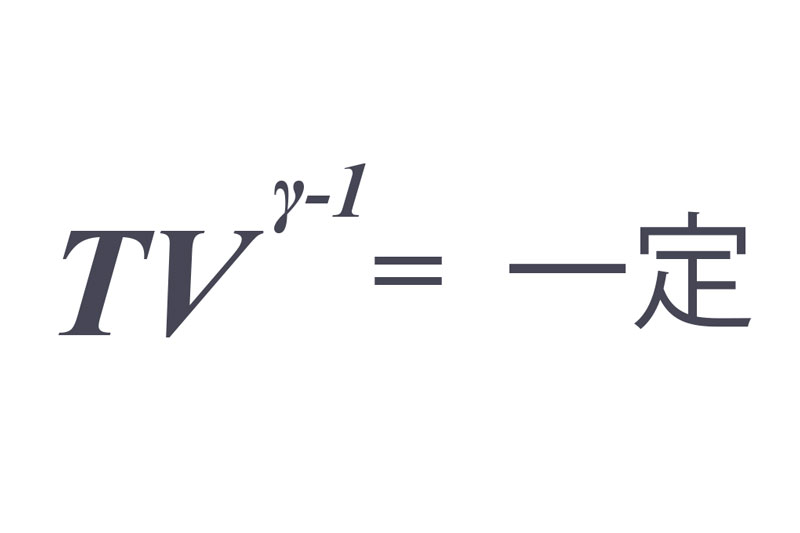
の関係が成り立ちます。ここでTは絶対温度、Vは体積、γは比熱比と呼ばれるものです。
今、空気はそのほとんどが窒素や酸素などの2原子分子でできているので、γ = 1.4 となります。(比熱比γは2原子分子理想気体の定圧比熱7/2と定積比熱5/2の比で7/5 = 1.4となる。)
この法則を利用するため、ボールの通り道だけに空気があり、その周りが真空(熱が伝わらない)、あるいは断熱材で覆ってある状況で、ボールが空気を押しつぶして行きます。ありえん?
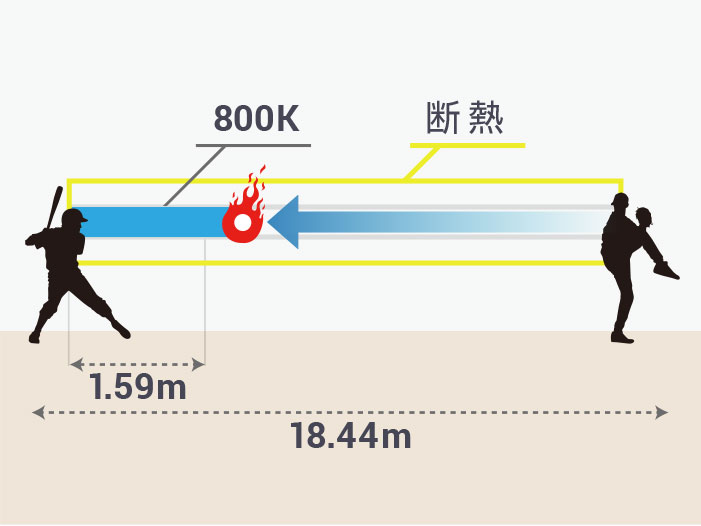
はじめは気温が27℃ = 300 K、燃え上がる時はおよそ800 K になるとします。ピッチャーからホームベースまでの18.44 mのあいだの空気を押しつぶしていき、バッターから何mの地点でボールが燃えるか計算すると、1.59 mになります。バッターの目の前まで来て燃え上がるんですね。いけるやん!
止まる魔球
しかしこの方法には弱点があります。
それは、「空気を押しつぶしていくごとに空気の圧力も高まり、ボールを減速させてしまうこと」です。
上の計算は実は、外から力を加えてボールをいつまでも押し込んで良いという条件の下での計算でした。上で速度は必要ないと書きましたが、それはボール押し込めるときのこと。実際には時速120 km程度では1.59 mに届く前に圧力に負けて止まってしまいます。
結局、ボールを投げただけで空気の円柱を18.44 mから1.59 mまで圧縮しようとすると相当な速度が必要となるのです。エネルギー保存則を使って計算したところ、
時速 563 km必要でした。
まとめ
実際に燃え上がる魔球を投げるよりも、比喩としての火の玉ストレートのほうが現実的だということがわかりました。これからも鍛錬に励みます。











.jpg)

















