ふくらPが小学生のときに考えたパズルとは？
――ふくらさんはパズルや謎解きを「解く」のが得意なだけではなく、パズルや謎解きを「作る」ことも行っています。パズルを作るようになったのはいつごろからでしょう？
ふくら 仕事としてやり始めたのは大学生になってからですけど、子どものころから親とか友達に自分が作った問題を出すのはよくやってました。でも、親に問題出すってみんなしますよね？
▲「親によく問題出してませんでした？」
――う〜ん、もしかしたらあったのかもしれないですけど覚えてないというか、QuizKnockに関係するクイズ好きな人ほどの当たり前のことでもないかもしれないです。
ふくら そうかぁ、僕はかなりやっていた気がしますね。今思えば僕の父は問題を出すのが好きで、と言ってもいわゆる「クイズ」っていう感じじゃなくて、物を手で隠して「どっちの手に持っているでしょう？」みたいな問題とかですけど。でもこれもクイズじゃないですか。
――あぁ〜なるほど。確かにそういうコミュニケーションはありますね。ちなみにふくらさんからはどんな問題を親御さんに出していたんですか？
ふくら え〜っと、なんだったっけなぁ。あっ、今100円玉って何枚か持ってます？
――お〜、ちょっとないかも。オフィスにいる人に借りてきます（一気に10枚集まった）。
ふくら ありがとうございます。これは小学生のときに考えた問題で、まず、100円玉を3枚置いたら三角形が作れるじゃないですか。で、上向きの三角形から100円玉を何枚動かすと逆三角形が作れるかっていうと、一番上の1枚を下に移動させれば作れますよね。
▲この三角形が……
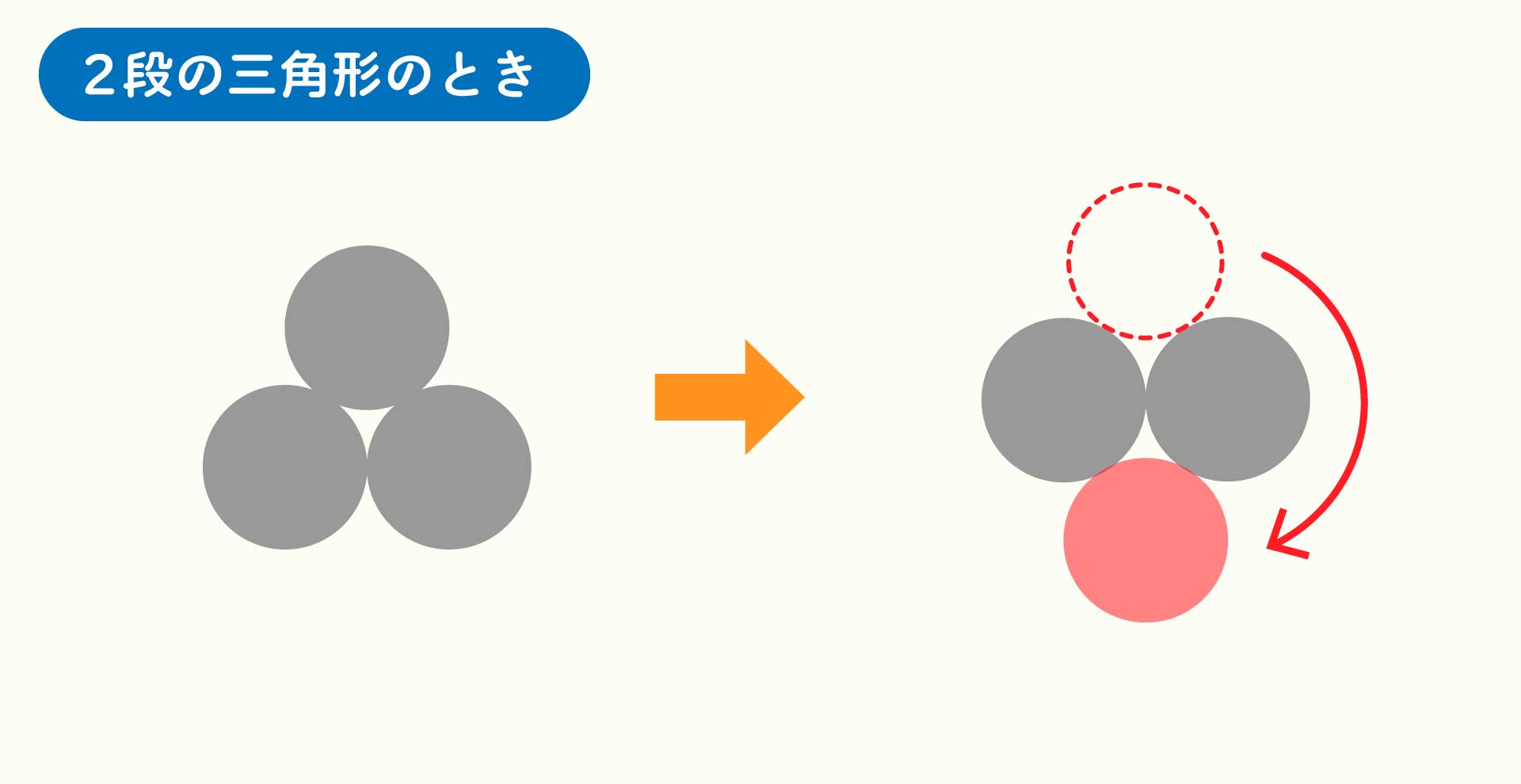▲こうなる
――はい、できますね。
ふくら じゃあ、三角形をもう1段分大きくします。6枚の100円玉で3段の三角形を作ったときは、最少で何枚移動させれば逆三角形になりますか？
ここで問題です
解くのが好き「でも問題がないから作ってた」
――すごい、結構難しいけど楽しい問題ですね。
ふくら 100円玉が1枚（1段）のときは0枚移動させると考えて、1段増やすたびに枚数は1,2,3……と増えていく。つまり、段数をnとしたときに逆三角形にできる最少の枚数は（n-1）になるっていう法則が成り立ってそうだなと。じゃあ、5段にしたときは4枚移動させればできるはずっていう仮説が立ちますけど、どうなるでしょう、という。
――えっ、小学生のときに等差数列の概念を理解していたということ……？
ふくら そうですね。でも、今のところ5段のときは5枚移動することでしか逆三角形にできてないんですよ。なので僕のなかでは未解決問題で……。
▲「これが5段になったときがまだわかってないんですよね……」
――未解決問題を親御さんに出題してたんですか？
ふくら 出しましたけど親はたぶん全然考えてないと思いますよ（笑）。確か、この問題は何かのパズル本に2段か3段のパターンが載っていて、それを拡張したんですよね。パズル本に載っていない類題を自分で考えて、自分で解くっていうのをよくやってました。
――すごい……。パズルを「解く」と「作る」、両方子どものころからやっていたということですけど、ふくらさんはどっちが好きだったんですか？
ふくら それはやっぱり解く方が好きでしたね。だから作りたくて作ってるというよりは、解く問題がなくなっちゃったから作ってたっていう感じで。本当になくなってはないんですけど（笑）、手の届く範囲にあるものがなくなっちゃったから。だから自分が解くために作ってたんですよね。
▲おそるべしふくらPの少年時代
――なるほど、クイズの作問は「これを答えにしたいからこの問題を作る」という側面が大きい気がしてるんですが、さっきの100円玉の問題のように自分でも解けない問題を作るというのがおもしろいですね。
ふくら 確かに、なんか数学者が未解決問題を自分で考えて、自分で証明してるのに近い気がしますね。もちろん、答えありきでクイズを作ることもあるんですけど、「これはどういう法則で並んでくるでしょう？」っていうのを考えるのが好きだったんですよ。
