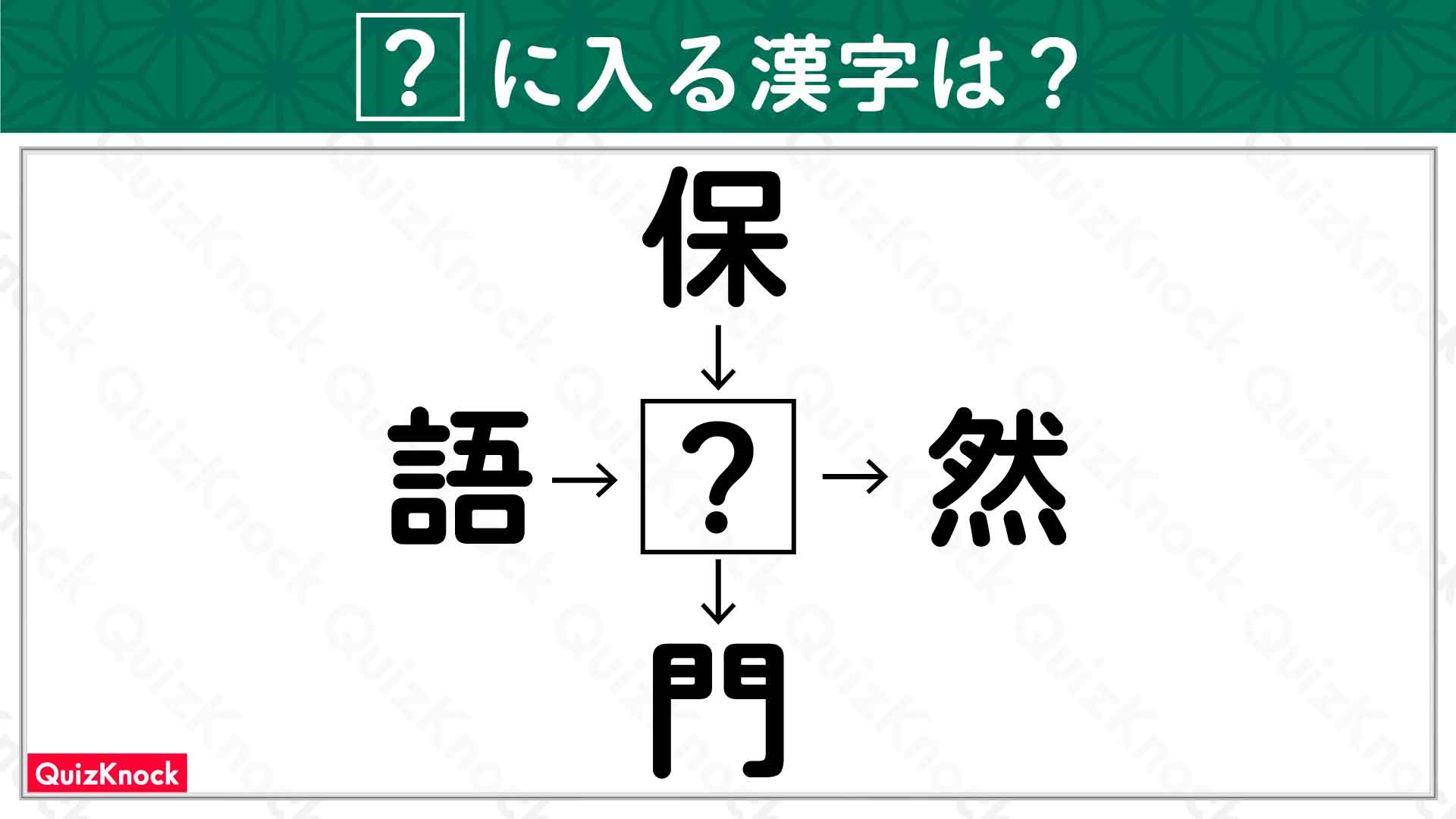
二階から目薬――。古くから伝わることわざで、高い場所から目薬をさすように、やり方が遠回しすぎて効果がないことをいいます。実際にそんなことをした人がいたかはともかく、私・千春は思うのです。
この世において「ふつうより高い」というステータスは大きなアドバンテージです。身近な例では、身長ですね。スタイルが良く見えますし、高いところにあるものも取りやすいです。スポーツでも高く跳び上がるバスケのダンクシュートは言うまでもなくかっこいいし、ボールを高く投げ上げて打つ卓球の「王子サーブ」も有名でしょう。誰もが憧れるルイ・ヴィトンのバッグも値段が高いし、日本レコード大賞のLiSAは声がとても高い。
▲高くてかっこいいものを挙げればキリがないやはり高さこそ至高。これが人生の方程式。
勘がいいみなさんならお気付きかと思いますが、ふつう目の数cm上からさす目薬をダイナミックに二階からさすということは……。
そう、かっこいいに決まっていますね。これはかなりイケてる。
▲かなりイケてます。絶対に……！ただし、それは「本当に二階から目薬をさすことができたら」という条件付きになることでしょう。難しそうではありますが、かっこよく目薬をさしたい欲は留まるところを知りません。
すぐにでも二階から目薬をさしたいところですが、大学院で毎日研究をする私は知っていることがあります。「闇雲に始めた実験は大抵うまくいかない」ということ。取り組むべき課題を明らかにし、見通しを立てることは必須です。二階から目薬をさすことの難易度を考えてみるべく、一旦は机に向かいます。
目次
◎ 「二階から目薬」の精度を求める
◎ 須貝博士に助けを求める
◎ 【実践】二階から目薬はさせるのか！？
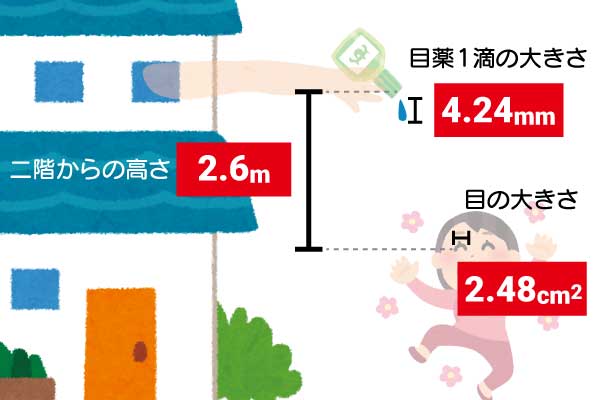
二階から目薬をさすために必要な精度を求める
二階から目薬を指すために必要な精度を計算してみます。つまり、具体的に「どのくらいの高さから」「どのくらいの的を狙うのか」などの条件を洗い出すのです。
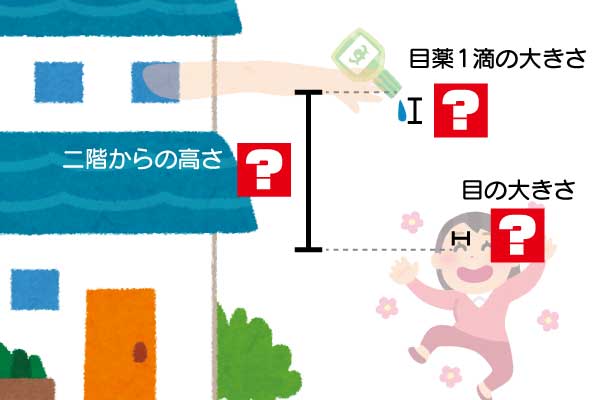▲まずは条件を整理しよう！目薬1滴分の大きさは？
まず、大学図書館で目薬についての文献を探してきました。『専門医のための眼科診療クオリファイ11（中山書店）』によると、目薬1滴は40µLだそうです。
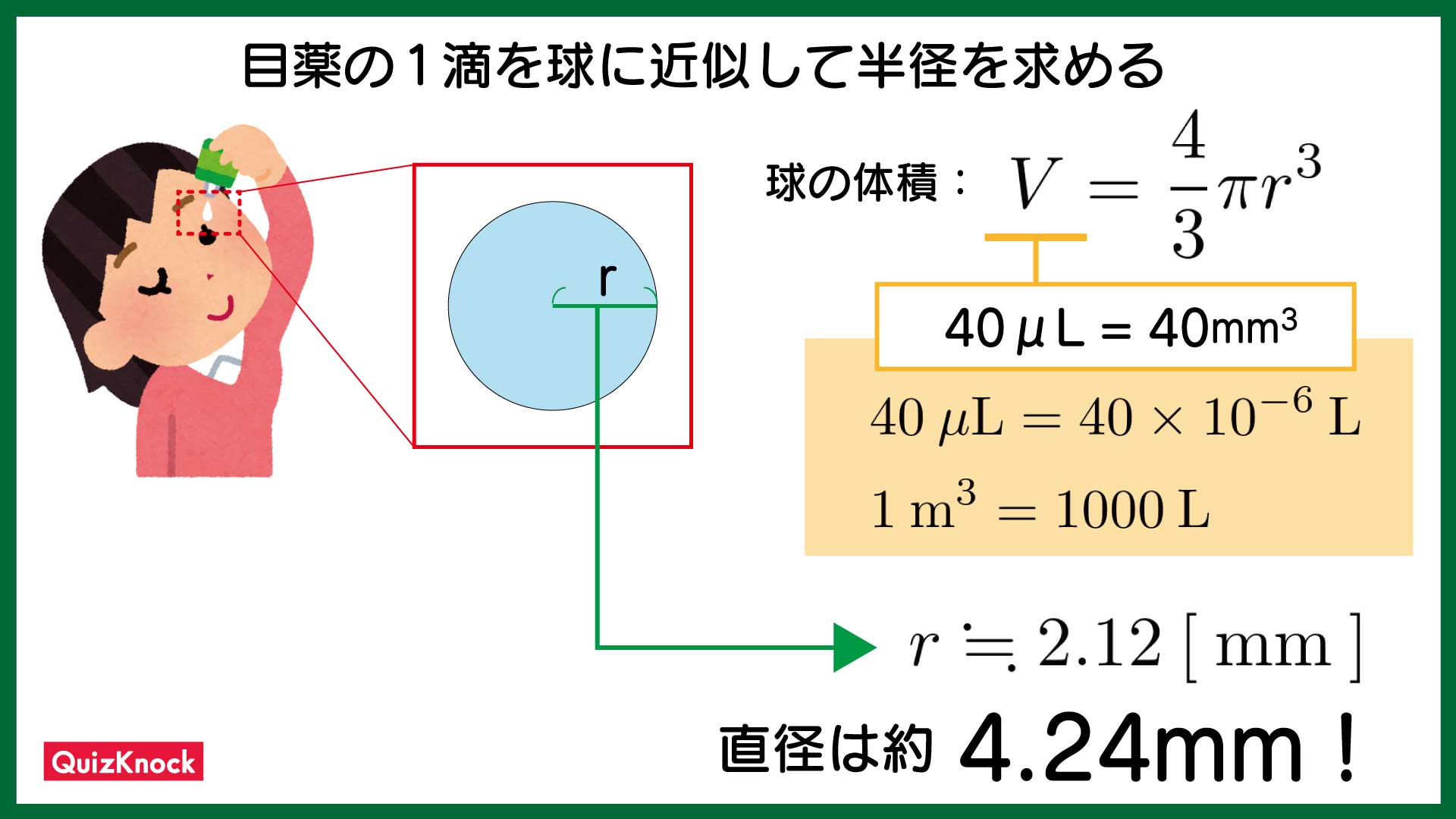▲目薬の体積から、球の大きさを求める！目薬の水滴を球とすると、その直径は約4.24mmとわかりました。とても小さくて若干の不安を覚えます。ただ、私は普段大学院で電子の動きに着目した研究をしています。電子の大きさは約1億分の1cm。それに比べたら目薬1滴はかなり大きいではありませんか。勇気が湧いてきました。
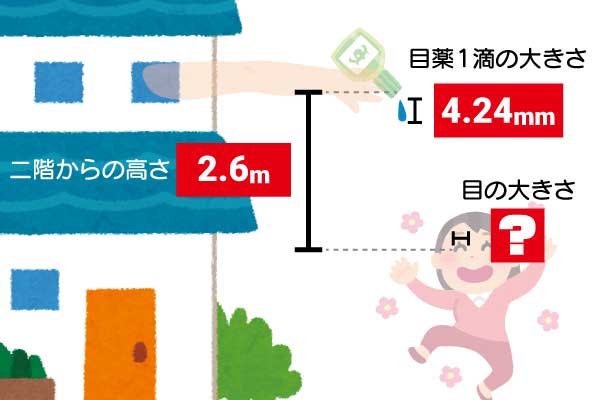
▲どうですか。勇気が湧いてくるでしょう二階の高さは？
では、二階の高さはどれくらいなんでしょう？ 考えたこともありませんでした。そんなときに頼りになるのは、様々な分野に精通したQuizKnockメンバーたち。さっそく建築学を学ぶ鞠乃ちゃんに助けを求めます。
鞠乃ちゃん、二階の高さってどれくらい？
いい質問！ 二階の高さといえば、私の中では2.6mがアツいんだよね。なんでかというと、まず私のリスペクトしている建築家がいつも2.6mで設計していて……（省略）
じゃあ、とりあえず二階の高さは2.6mでいいってことね？
そうそう、あと2.6mは個人的に階段の計算がしやすいから好き！ あとはね……（長かったので省略）
なるほど。細かいことはよくわかりませんでしたが、2.6mでいいようです。愛が溢れていますし、階段の計算がしやすいということがわかりました。ただし今回は階段の計算はしません。
▲だんだんわかってきた！※すごく厳密に計算するなら、二階からの高さは「点眼される人の目の高さから二階からさす目薬の高さ」を求めたほうがよいですが、簡単にするため、ここでは二階にいる人は点眼される人と同じ身長で目の高さから点眼すると仮定して二階の高さ（2.6m）を用いることにします。
目の大きさを全力で計算する
次に必要なのは、的となる目の大きさです。これは個人差がありそうですが、ここでは私の左目の大きさを求めてみます。
目の形は複雑なので長方形にも円にも近似しづらく、簡単に面積を求めることはできなそうです。
そこで、ここでは目の形を関数化して計算することにしました。左目の写真を撮り、Excel上で目頭から目尻までの輪郭を座標に変換していきます。上ライン・下ラインと2つの関数に近似しました。この関数を積分することで、私の左目の面積が計算できるのです。
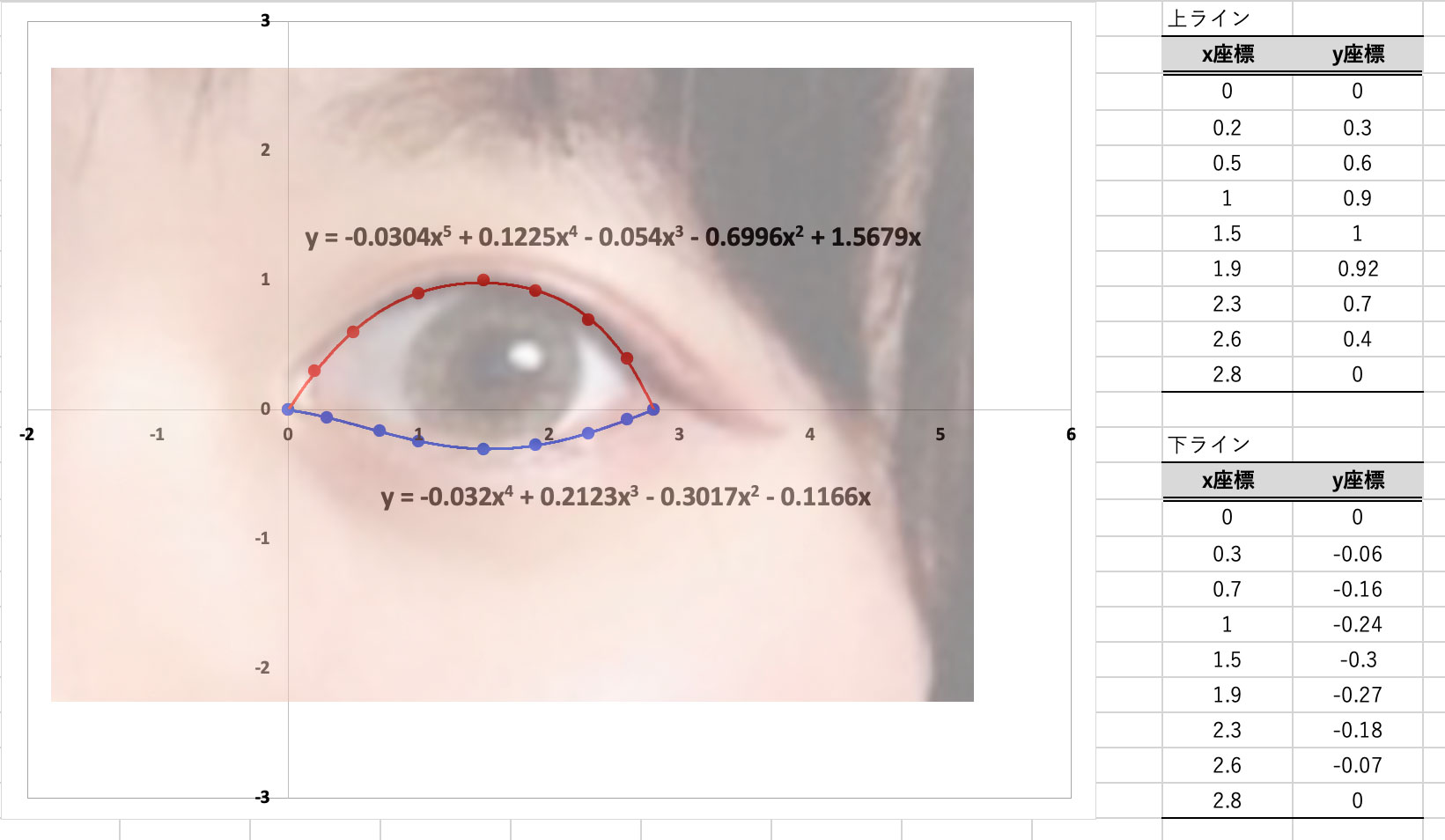▲軸の単位はcm。この写真を撮るために少々目をかっ開いているため、いつもより少し大きいかもしれません。アイラインで目の大きさを盛っているのがバレてしまいました私の左目を関数化し、5次式と4次式で近似した式がこちら！
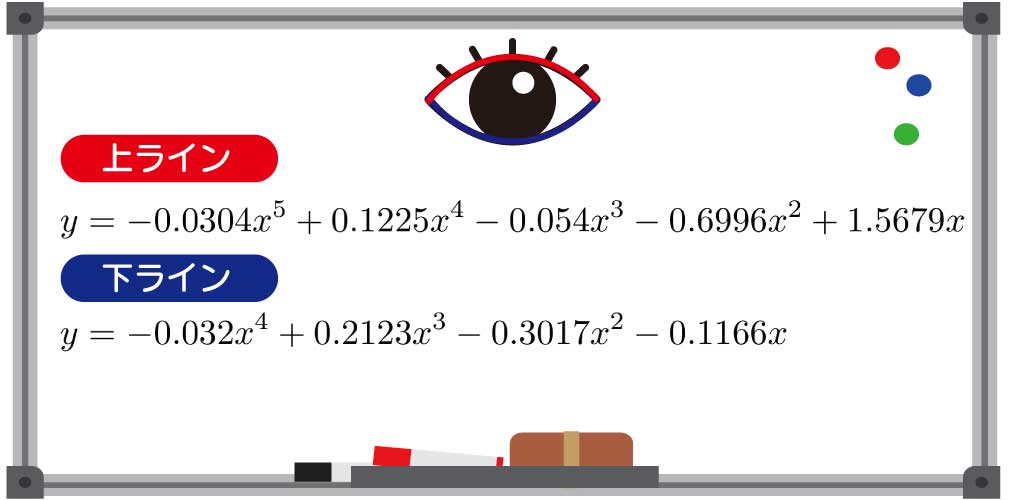▲上記の関数をプロットすると、私の左目のグラフが描けます。どうぞお試しくださいませこの関数を積分して面積を求めます。積分には、便利なWolframAlphaというツールを使いました。横で数学科ライターの鹿野くんが「手計算しようぜ」などと言っていますが、聞こえなかったことにします。
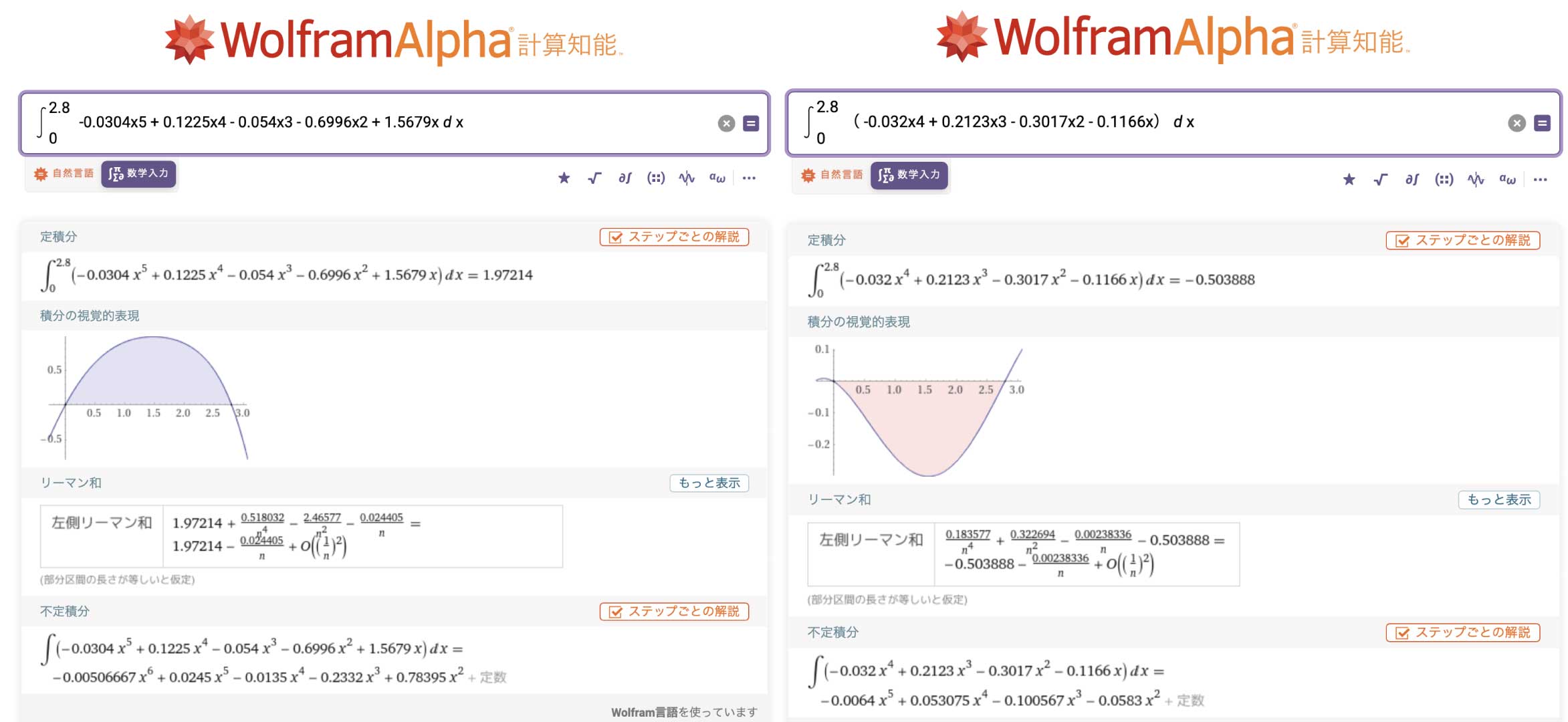▲こんなにも簡単に積分できるなんて……！上ライン・下ラインをそれぞれ積分した値を合計し、私の左目の面積は約2.48cm2と求められました。うーん、もう少し大きい予想だったのですが。
二階から落とした目薬が目に入るためには
さて、やっと条件が揃いました。
▲準備は万端！これらの値を使って、二階から落とした目薬が目に入るための条件を計算していきます。
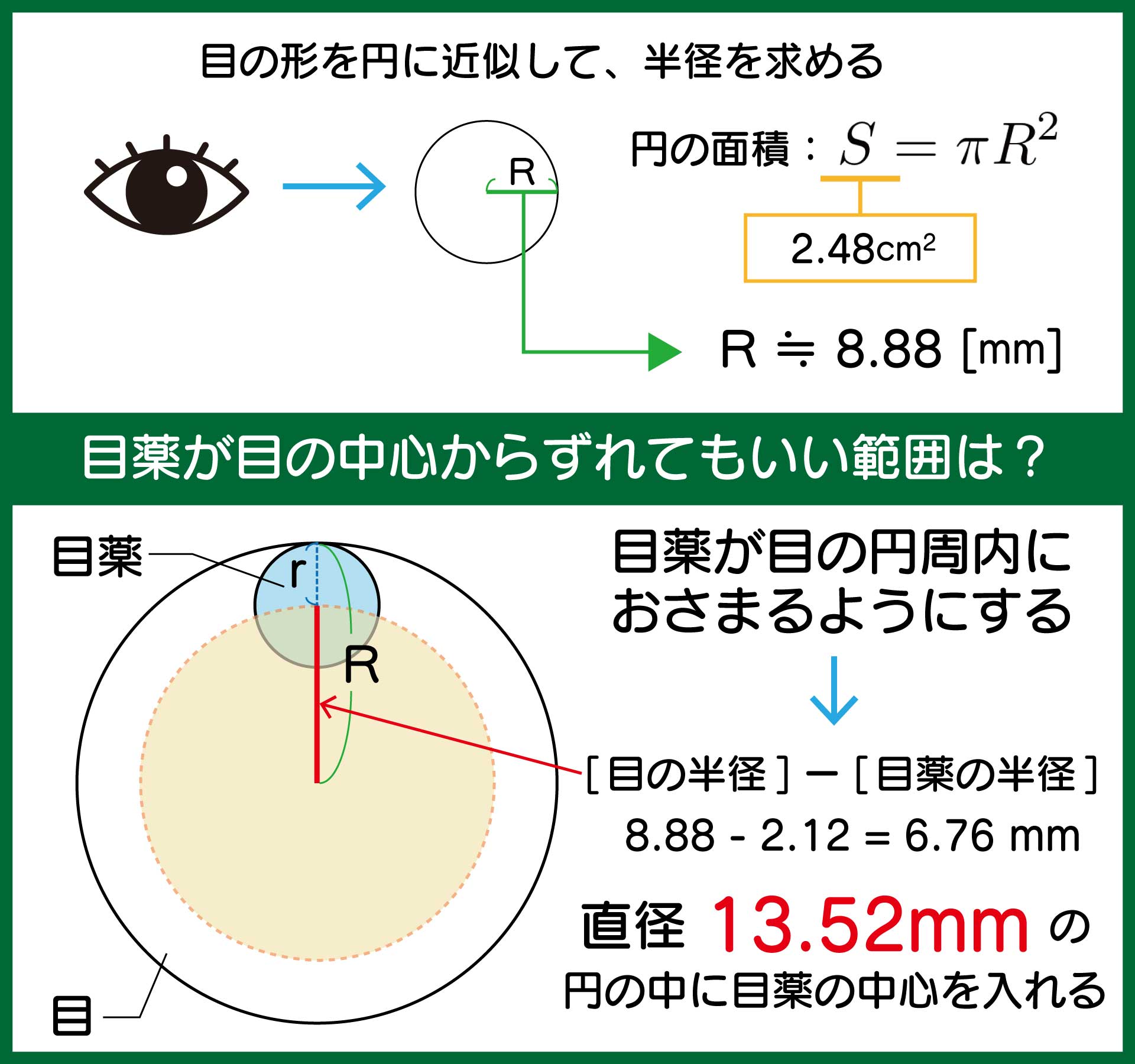
二階から目薬を落として目に入るには、直径13.52mmの円に直径4.24mmの1滴を入れないといけないということがわかりました。
……つまりこれは、どれくらい難しいんでしょうか？ 夢中で突っ走ってきたものの、結局よくわからないところに辿り着いてしまったかもしれません。
▲皆さんもそんな経験ありませんか？何か難しさがわかりやすいものに例えたいところです。
的を狙って球形のものを投下するものといえば……。野球だ！
野球といえば、QuizKnockには毎週野球をし、かつ物理にも詳しい須貝駿貴博士（学術）がいるではありませんか。
