解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解法のポイントは「同じ長さを見つける」ことです。
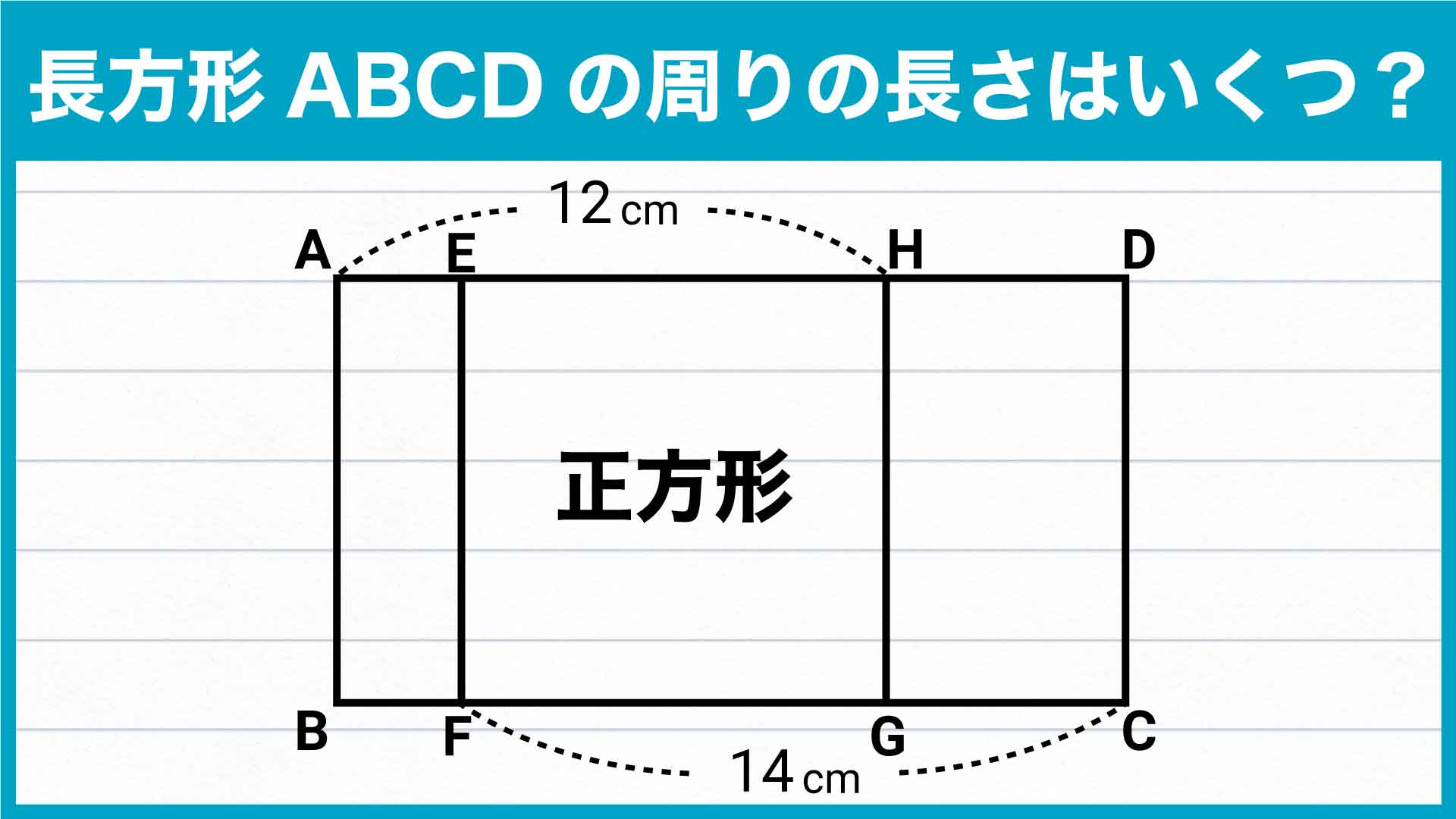
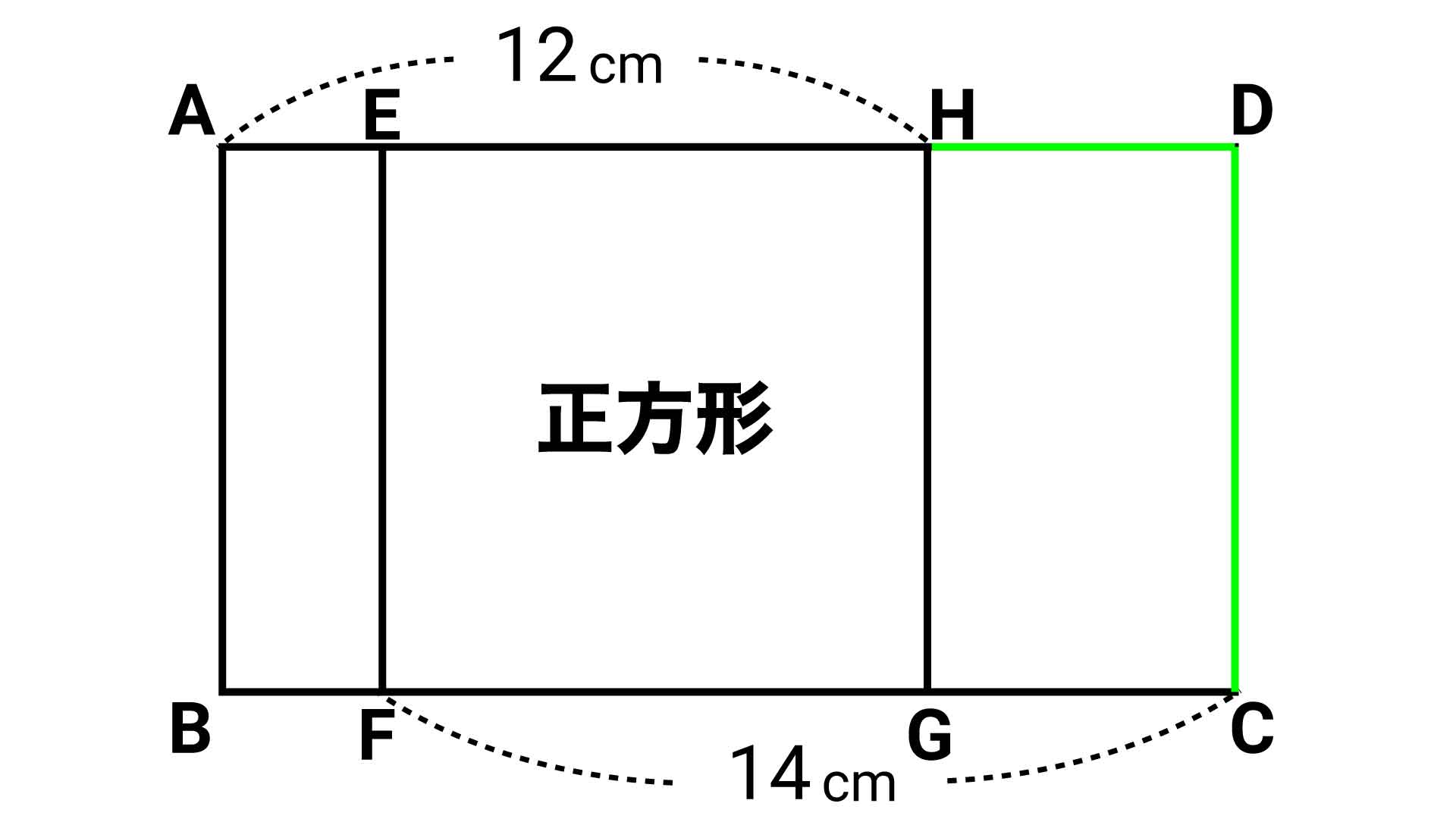
既に線分AH=12cm、線分FC=14cmであることがわかっているので、折れ線ABFと折れ線CDHの長さがわかれば、長方形の周りの長さを求めることができます。
このため、これらの折れ線について、長さがわかっている線分AHと線分FCと同じ長さになるところを見つけると、スムーズに解くことができます。
同じ長さなのは、どことどこ?
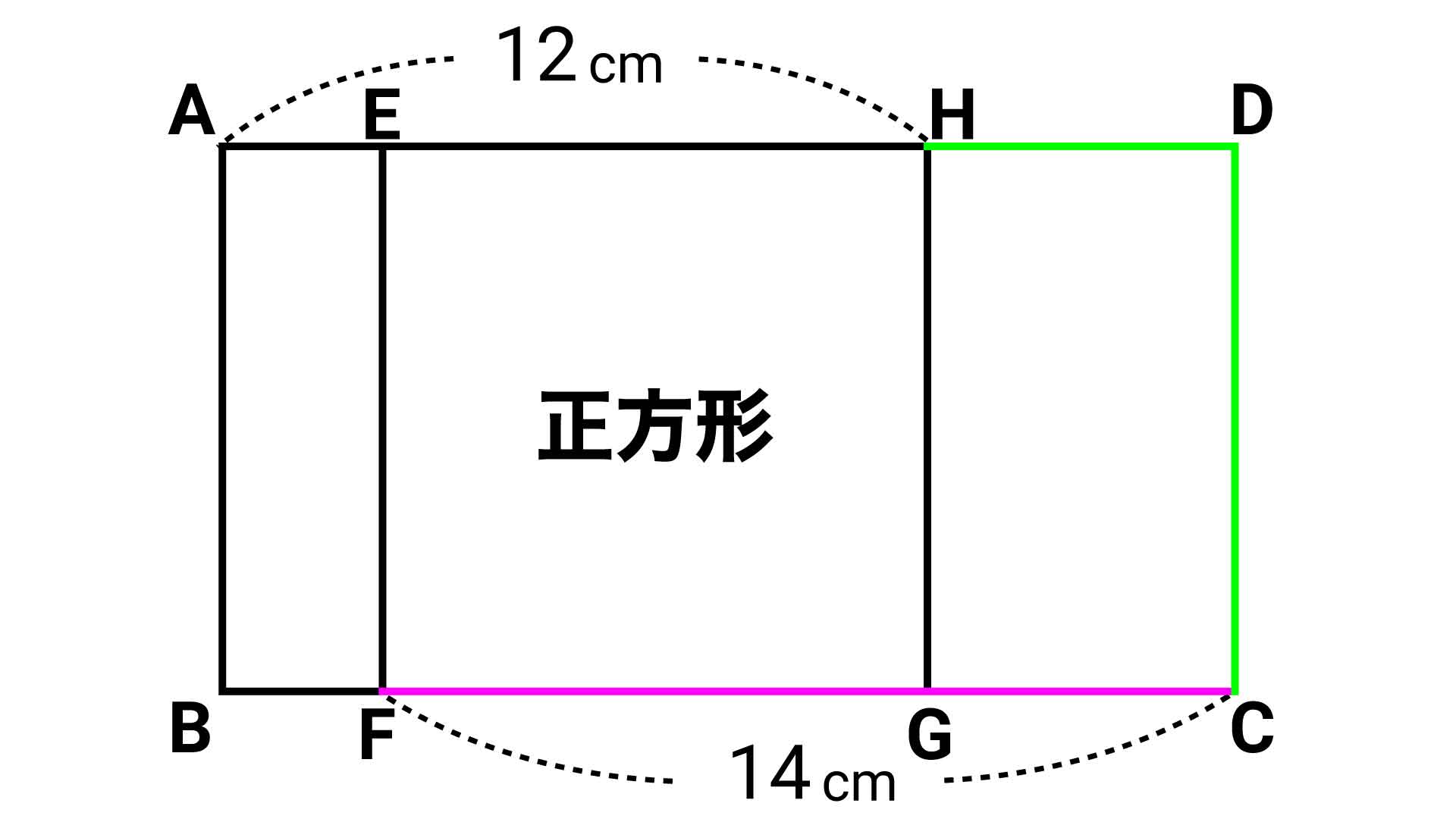
まずは折れ線ABF(AB+BF)について考えます。
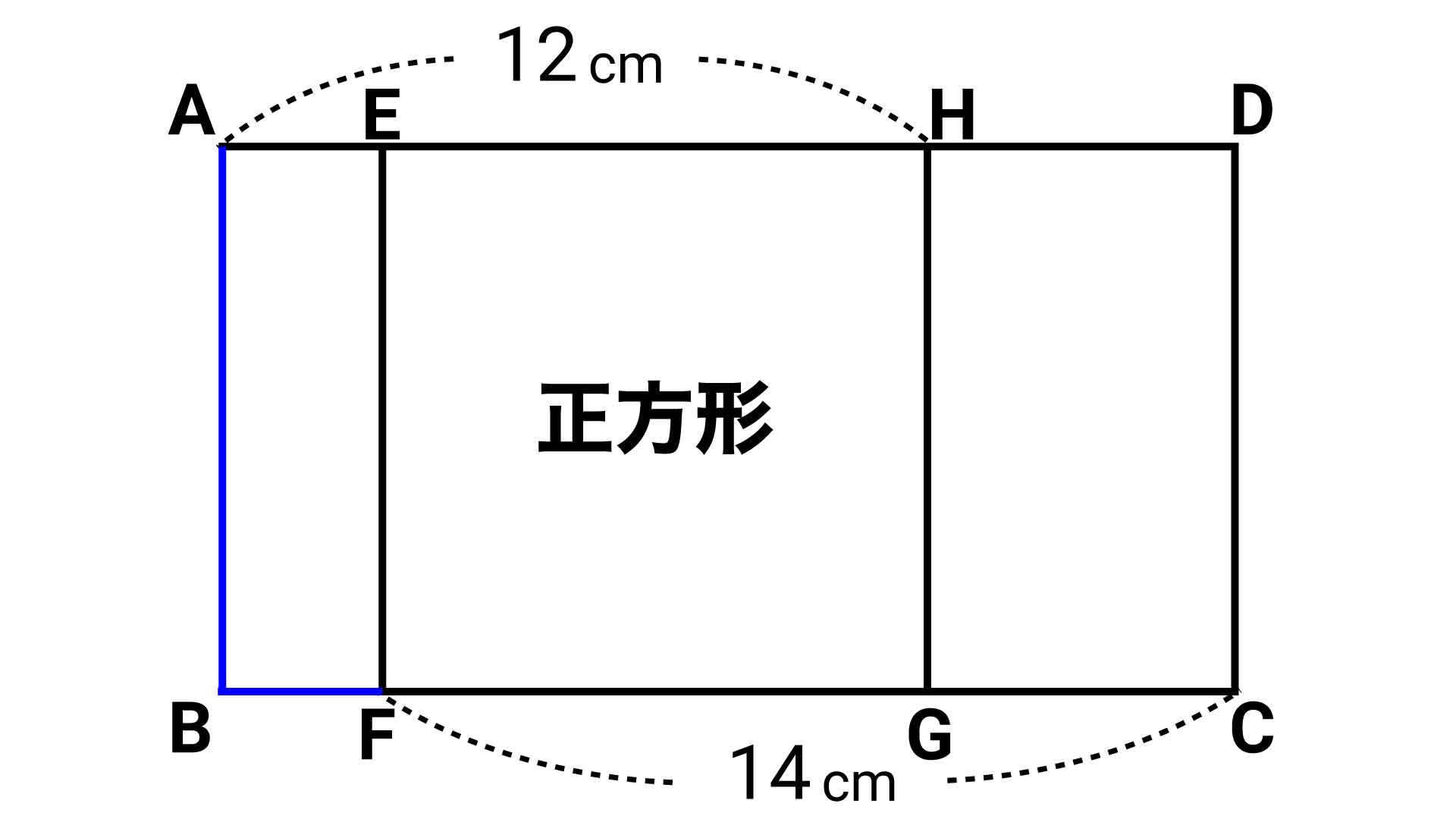
四角形ABFEは長方形(すべての内角が90度)なので、ABはEFと同じ長さ、つまりABは正方形の1辺と同じ長さになります。
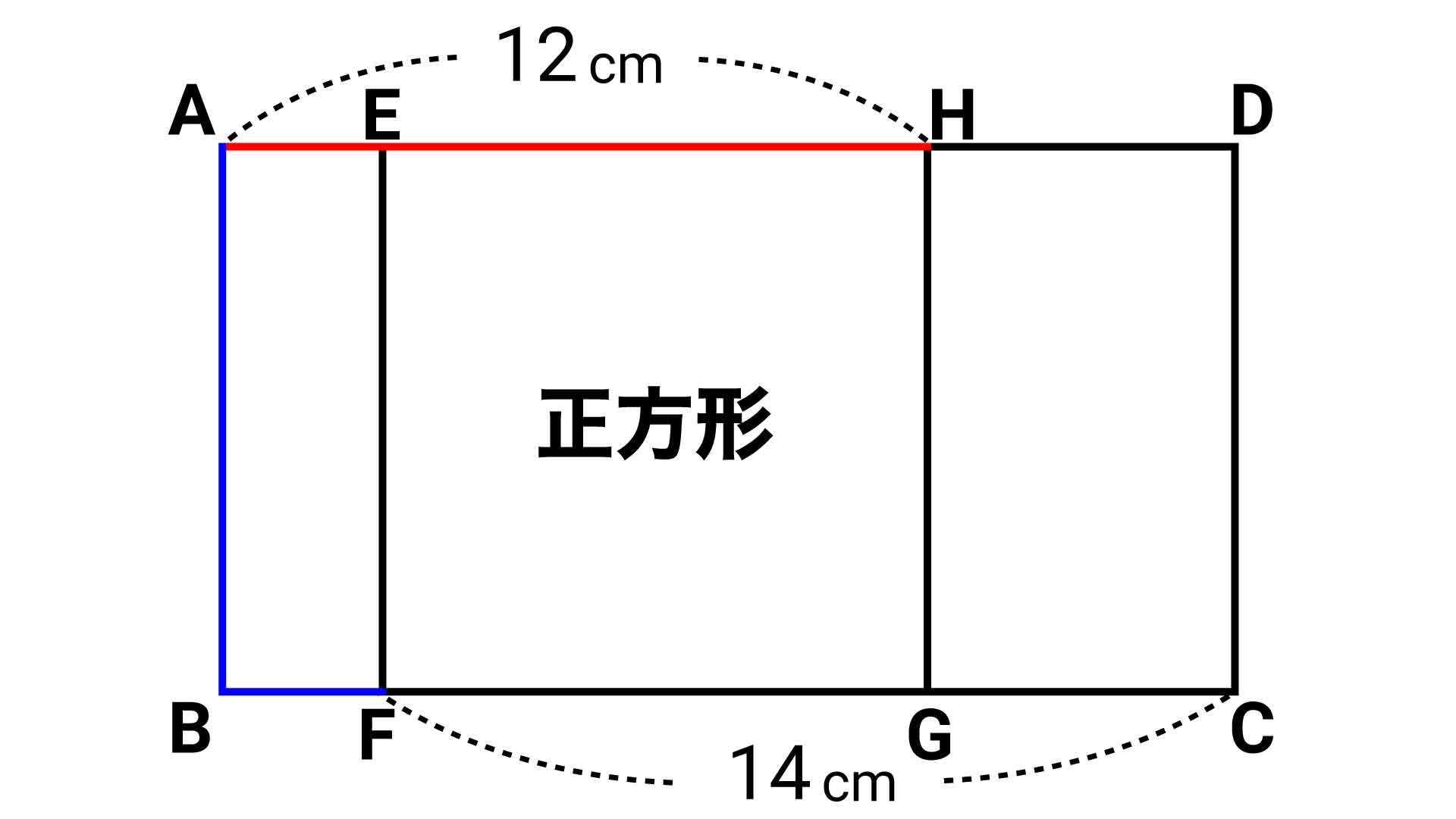
また、長方形ABFEについて、BF=AEです。このことから、折れ線ABFの長さは正方形の1辺+AEの長さと等しくなります。それは、まさに線分AHの長さです。
以上より、折れ線ABF(AB+BF)の長さは、線分AHの長さ(AE+EH)と同じ、12cmであることがわかります。
あとは折れ線CDHを求めるだけ
これと全く同じことを、折れ線CDH(CD+DH)についても行います。
折れ線CDHの長さは、正方形の1辺の長さ+DHであるため、線分FC(FG+GC)の長さと等しいことがわかります。つまり、14cmです。
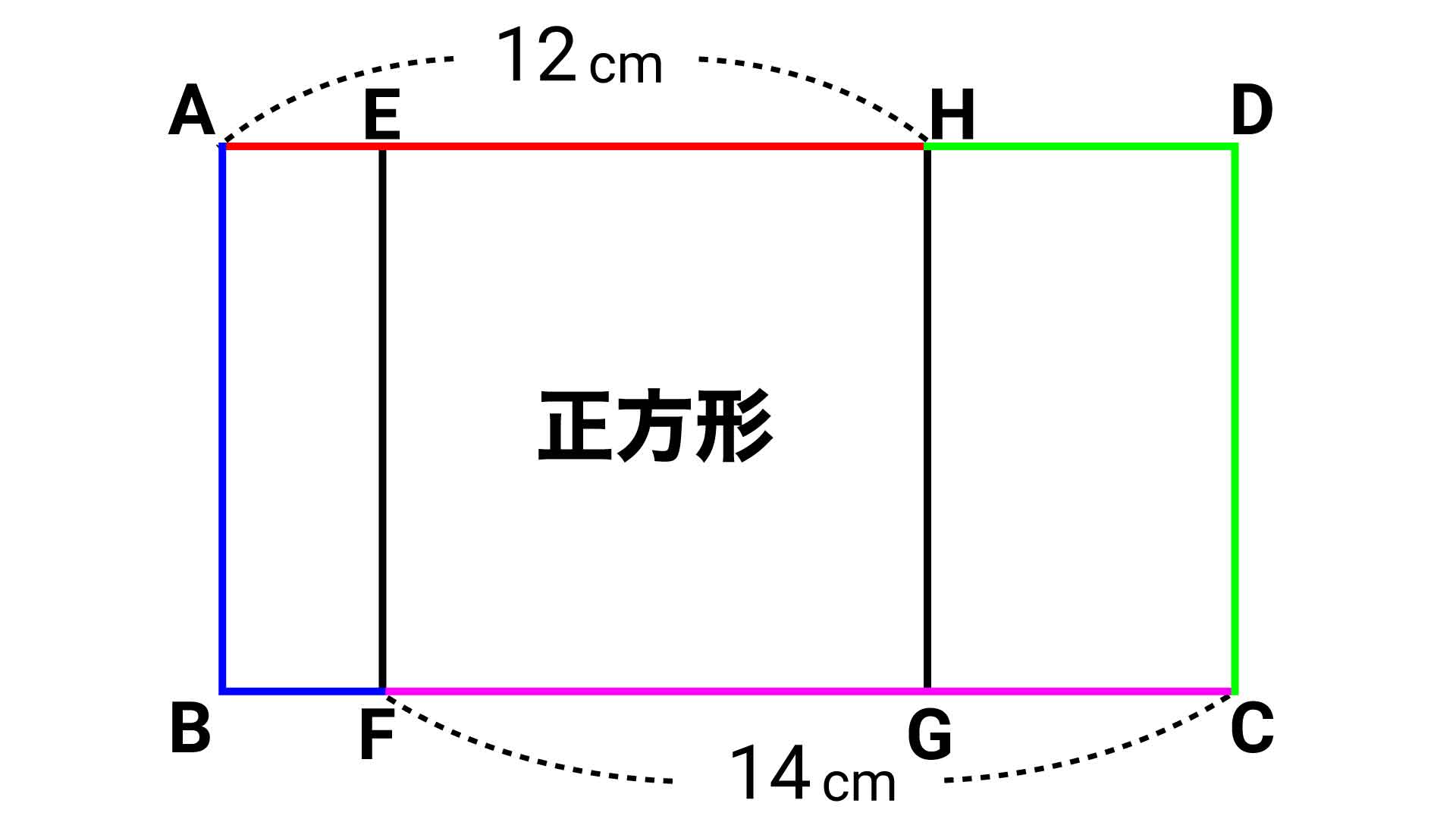
以上から、長方形ABCDの周りの長さ(線分AH+折れ線ABF+線分FC+折れ線CDH)は、
12+12+14+14=52cm
となります。
答え:52cm
正方形を巧みに使いこなせるかどうかがカギとなる問題でした。
それでは。
【あわせて読みたい】









.jpg)









.jpg)







