解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです。
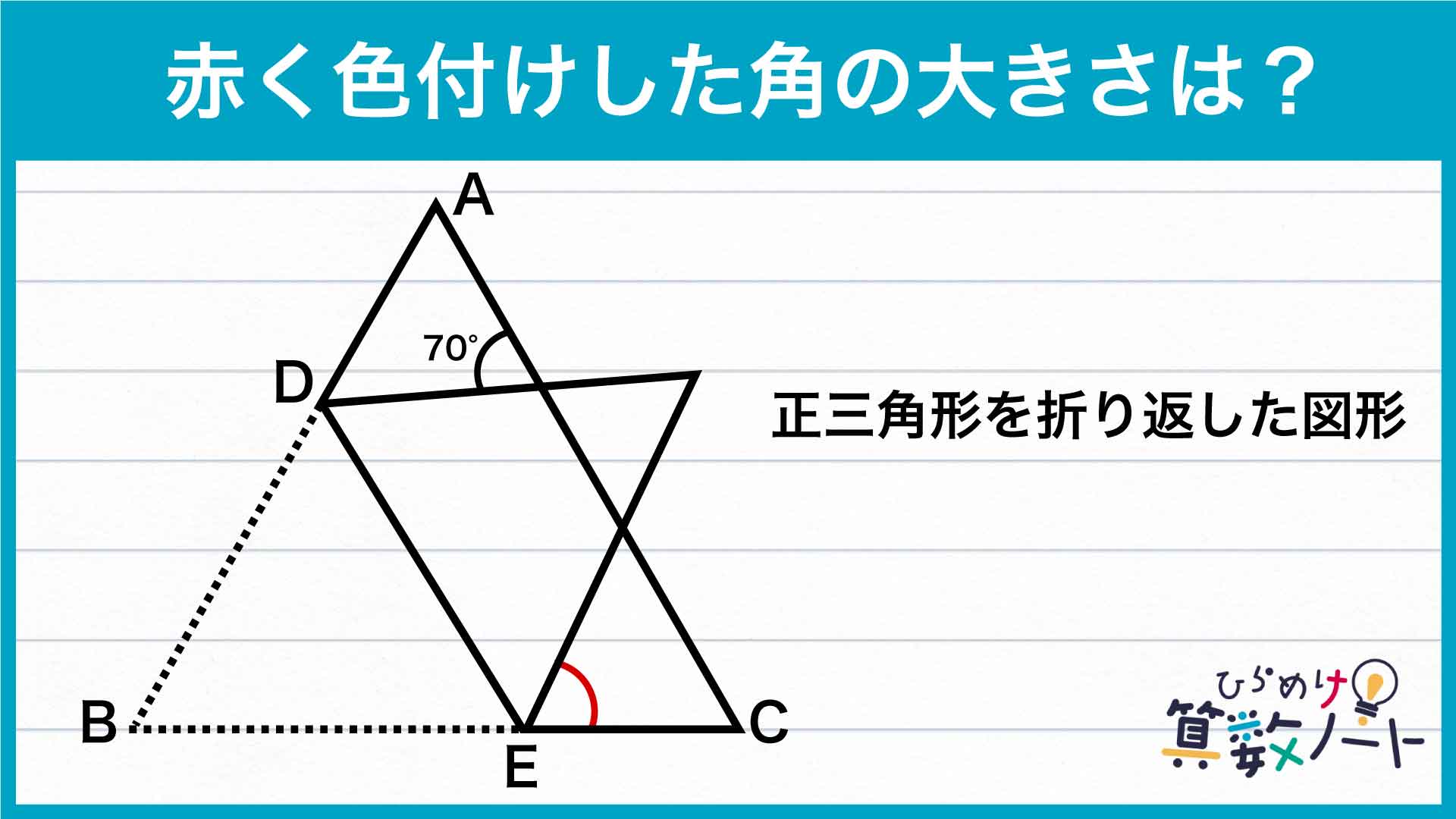
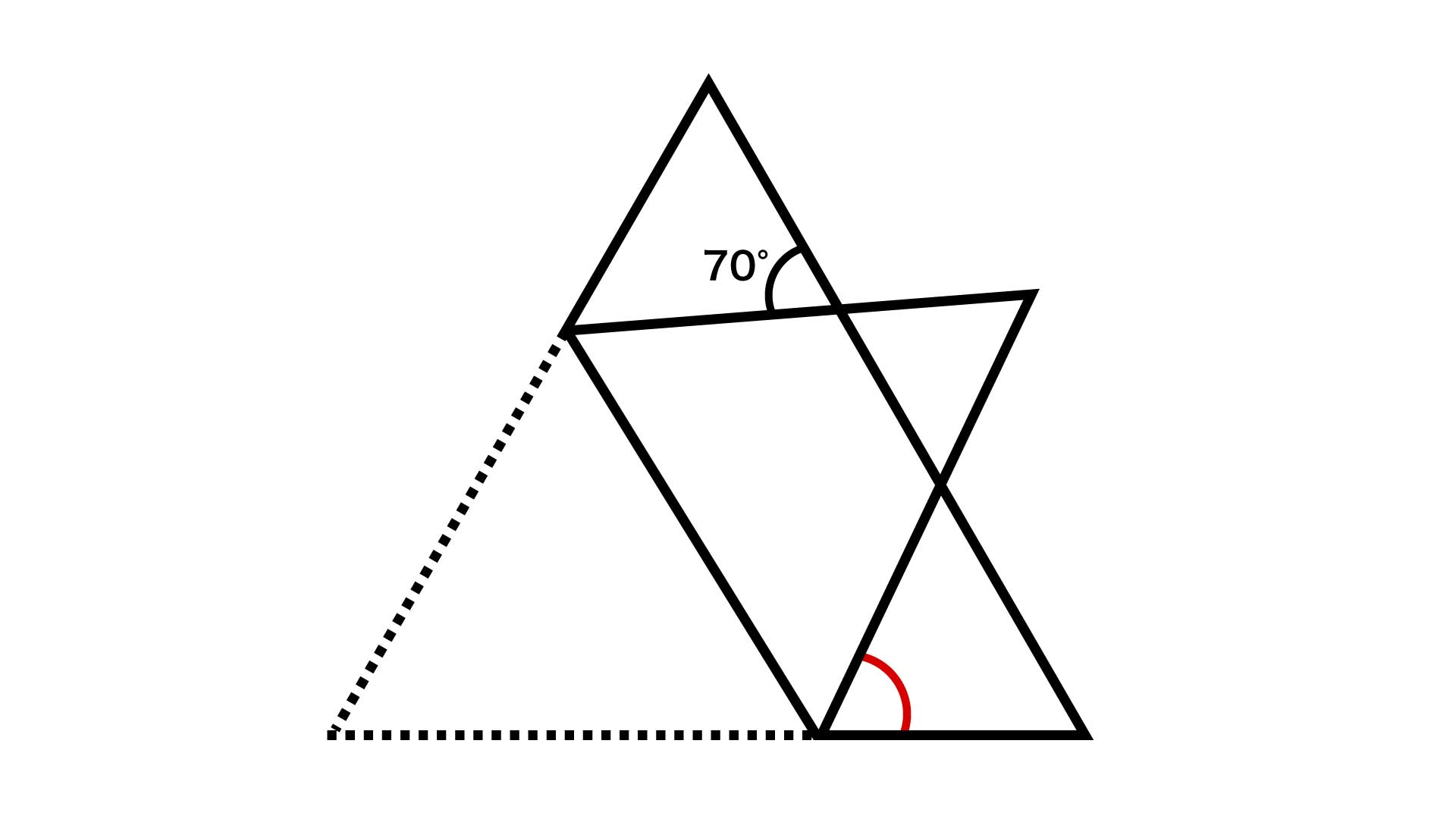
今回のポイントは、「等しい角度を見つける」ことです。
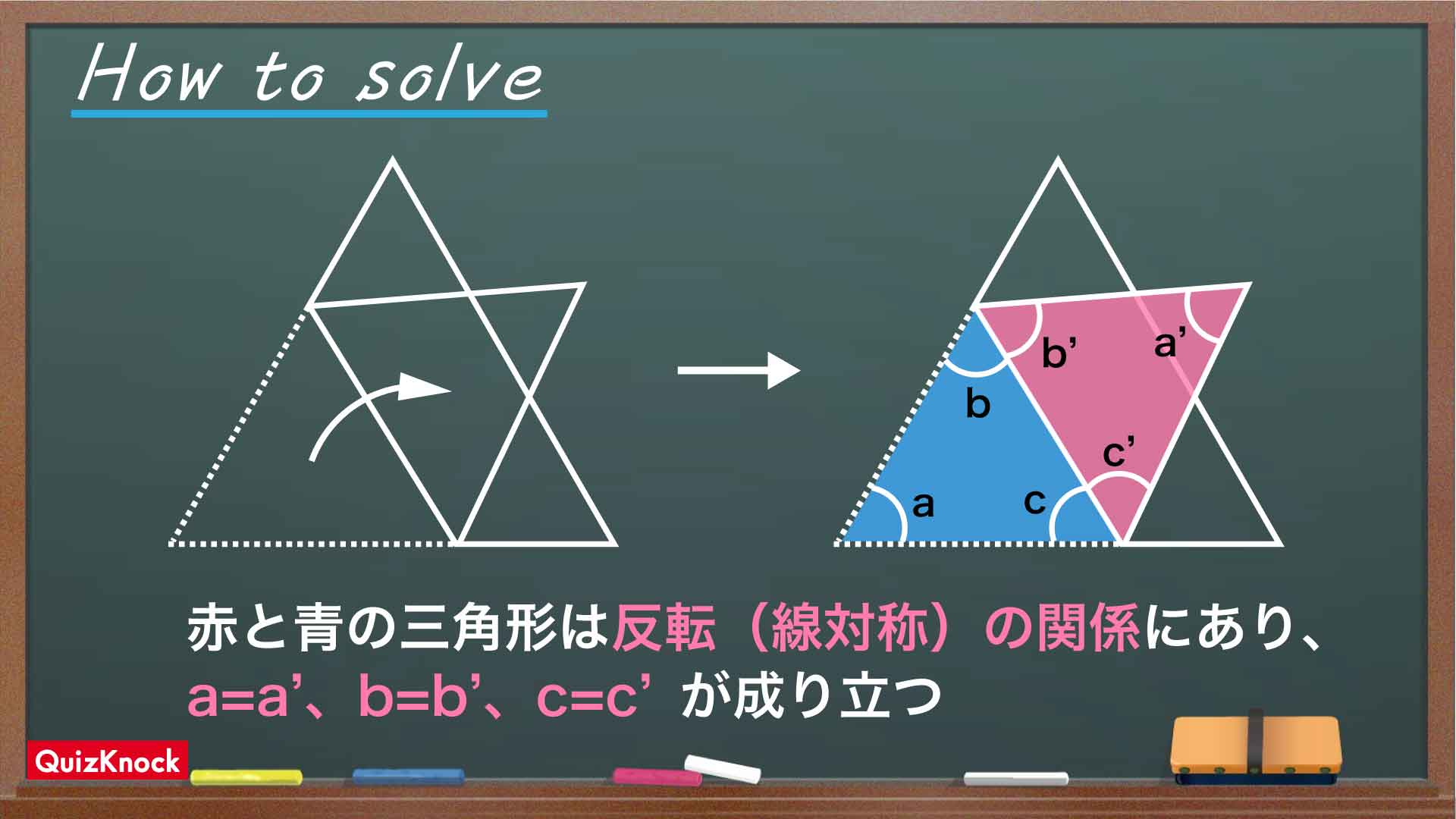
図形の一部を折り返すと、左右反転した線対称（ある直線を折り目にして折り返したときにぴったり重なる関係）の図形が現れます。
もとの図形と線対称の図形の内角は等しいので、この条件は角度を求めるうえで重要な情報になります。
以上を踏まえ、問題を解いていきましょう！
正三角形の内角に注目
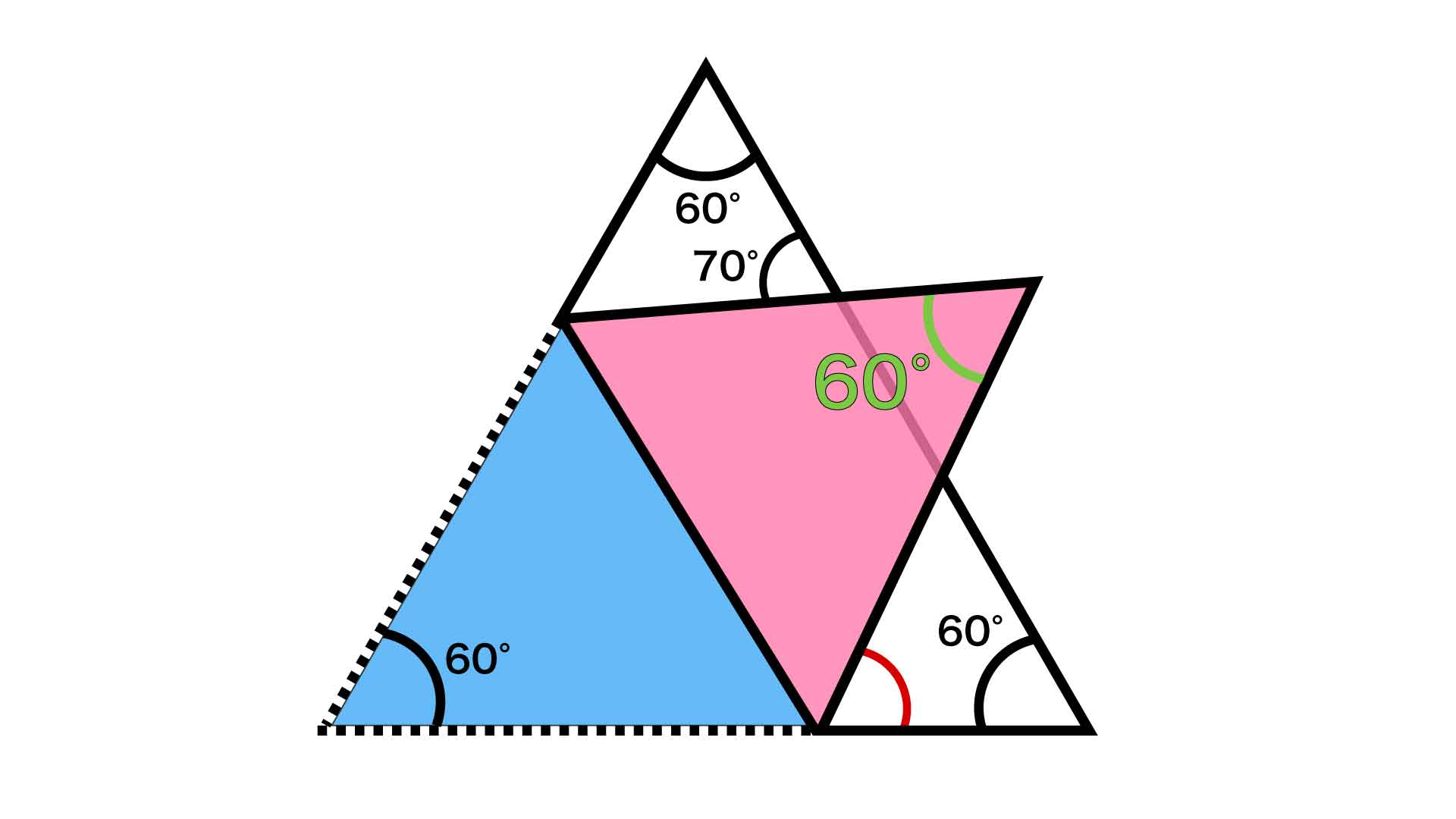
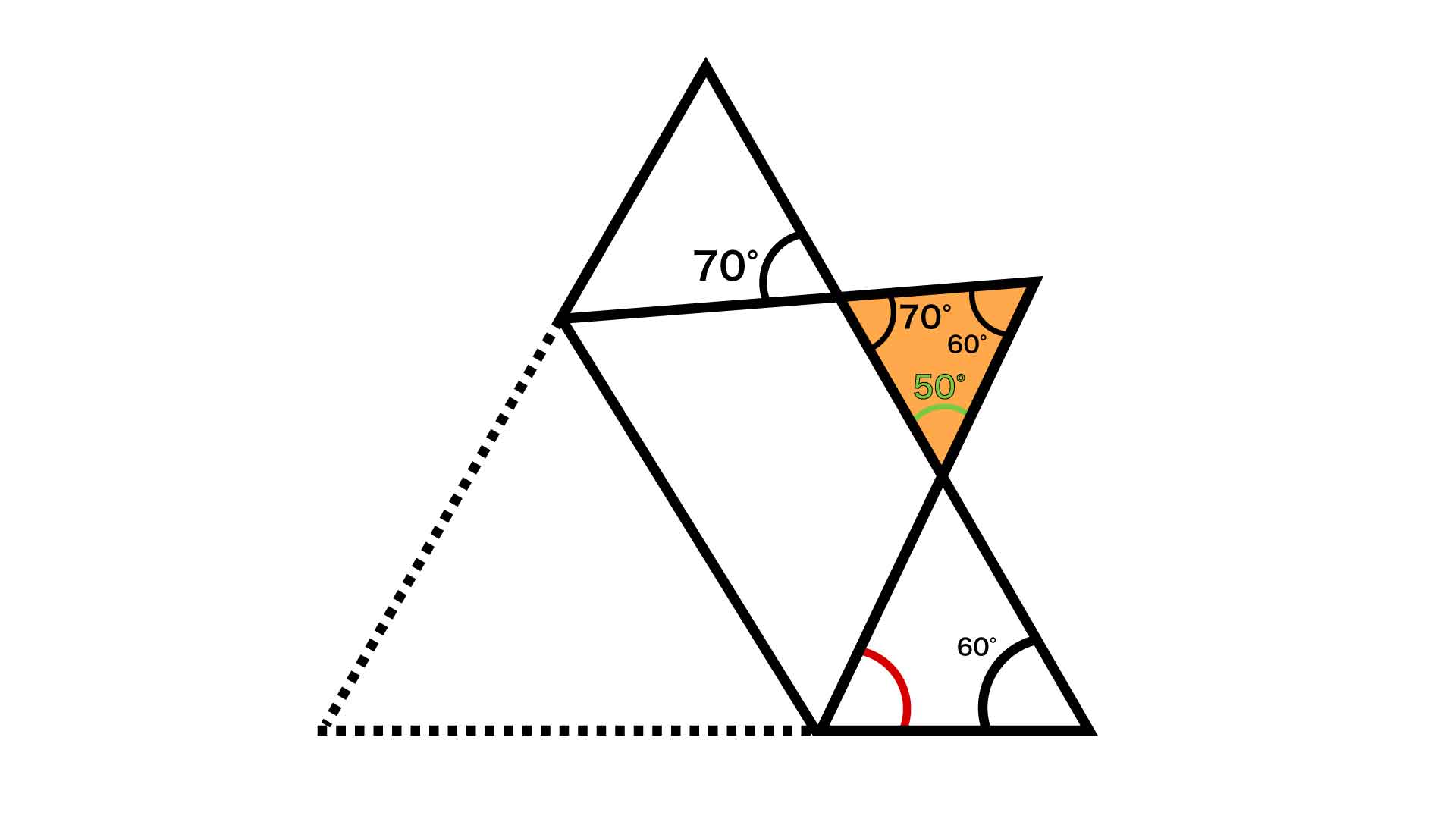
折り返す前の図形は正三角形なので、それぞれの内角の大きさは60度です。そして、下図の赤い三角形と青い三角形は線対称の関係なので、緑色の角の大きさも60度になります。
角度を順に計算
下図でオレンジ色で示した三角形に注目します。向かい合った角の大きさは等しいので、与えられた70度の角と向かい合った左上の角は70度となります。また先ほど求めたように、折り返した部分の角の大きさは60度になります。したがって、残った緑色の角の大きさは、三角形の内角の和が180度であることから、180-70-60=50度と求められます。
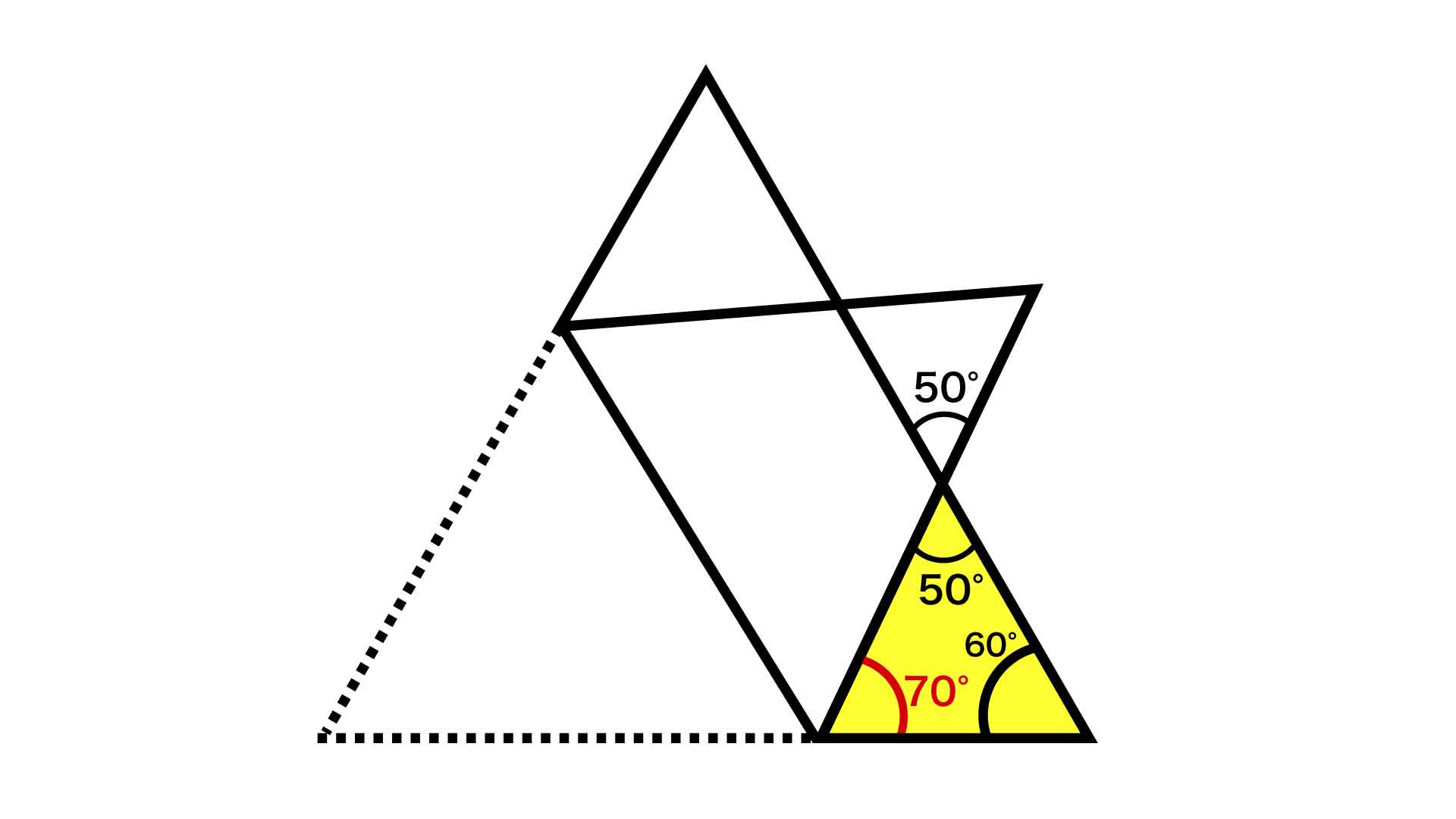
次に、下図で黄色で示した三角形に注目します。先ほど求めた50度の角と向かい合っている角の大きさも50度になります。また右下の角は、正三角形の内角なので60度となります。
したがって、残った赤色の角の大きさは、三角形の内角の和は180度であることから、180-50-60=70度と求められます。
答え：70度
それでは、次回の算数ノートでお会いしましょう。
「ひらめけ！算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】
