解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
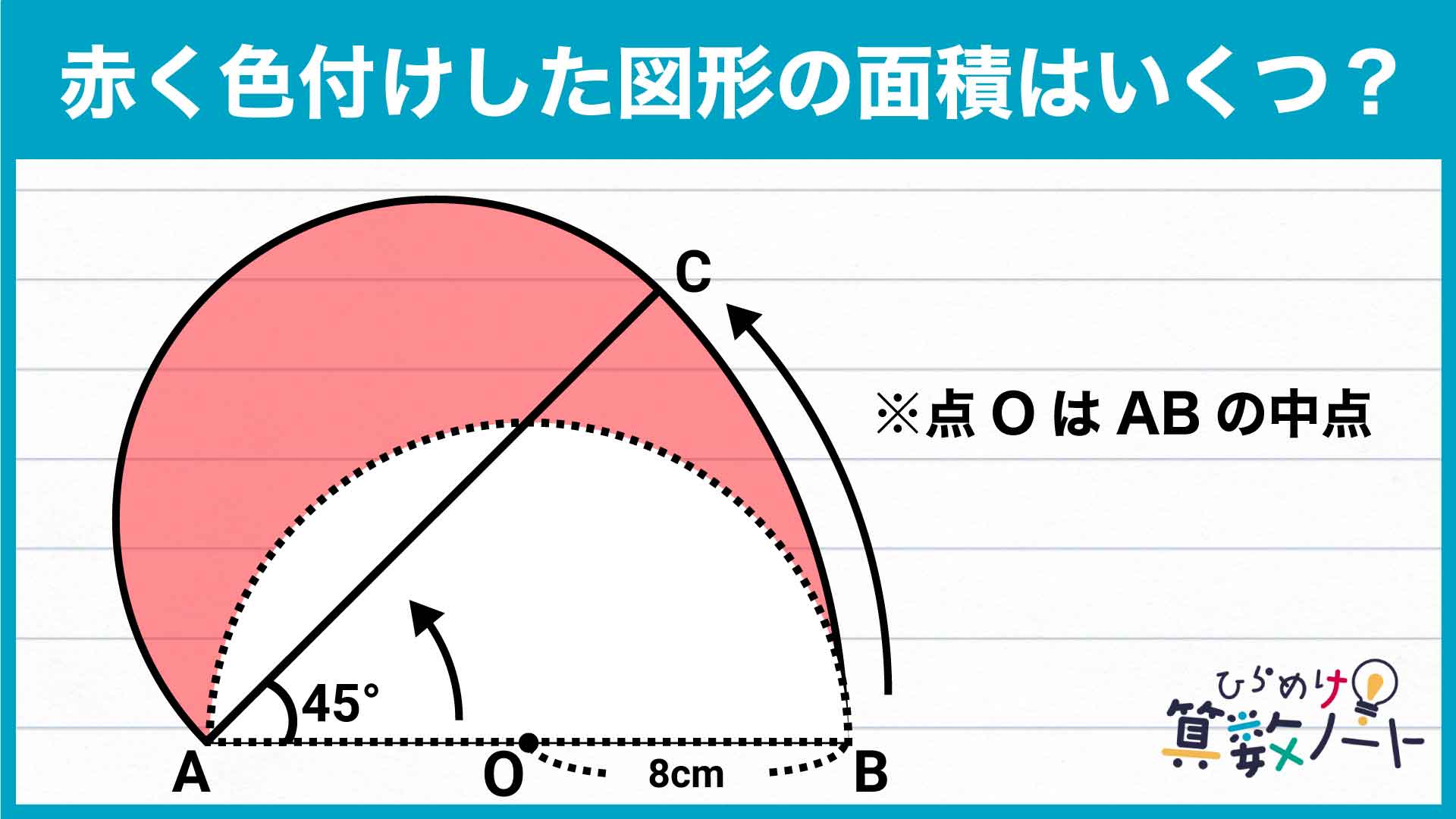
今回のポイントは、「引き算を使って面積を求める」ことです。
赤く塗られた図形は、どう補助線を引いても面積を直接求めることはできません。そこで、「足してダメなら引いてみな」です。
描かれた全体の図形の面積から、塗られていない部分の面積を引くことで、目的の図形を浮き彫りにしましょう。今回は、以下のように足し引きすることで、答えを導くことができます。
この図の流れに沿って、順に解いていきましょう!
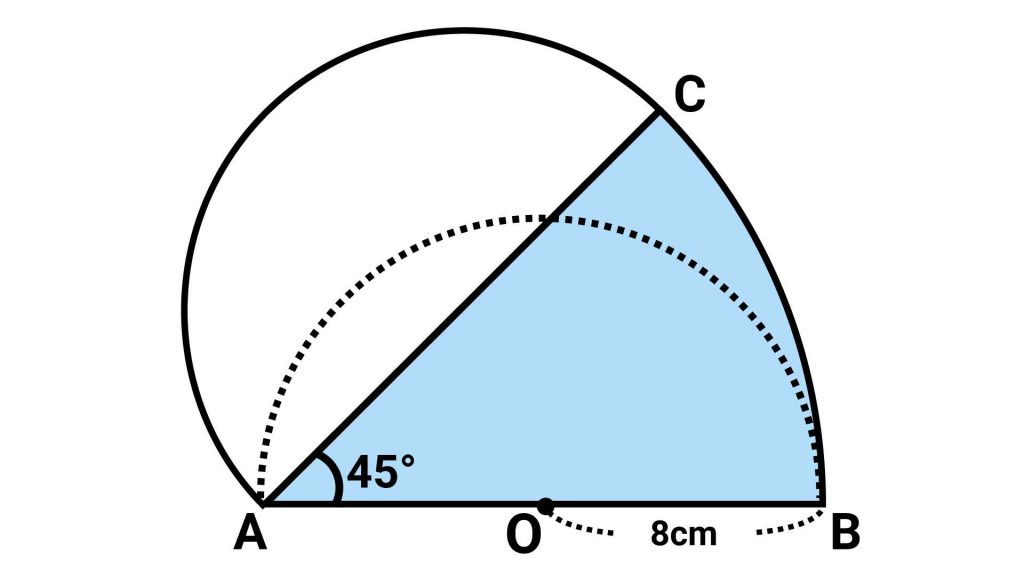
おうぎ形の面積を求める
まず、以下の図で示したおうぎ形の面積を求めます。
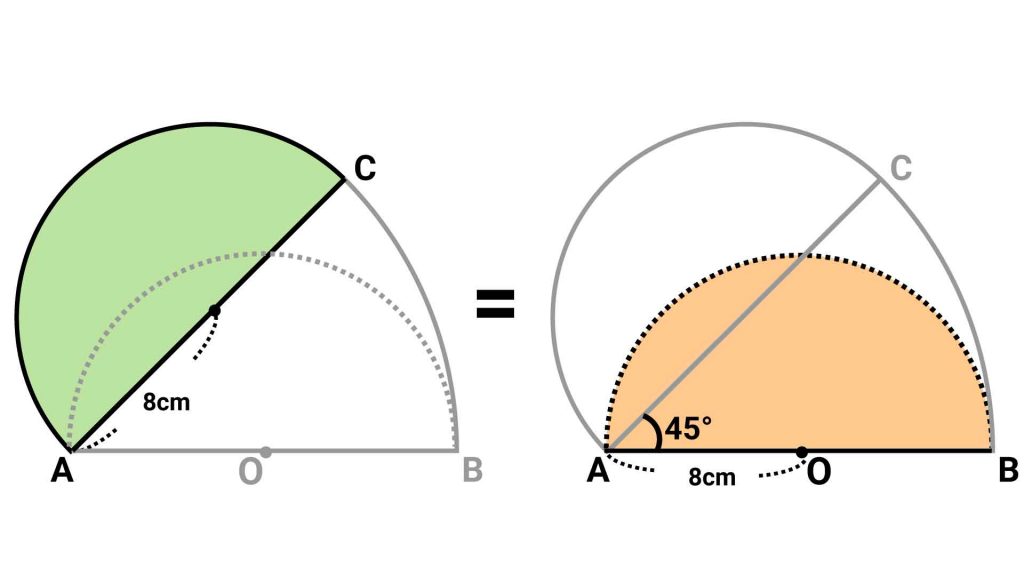
半径16cmで中心角45度のおうぎ形なので、面積は16×16×π×45/360=32πcm2となります。
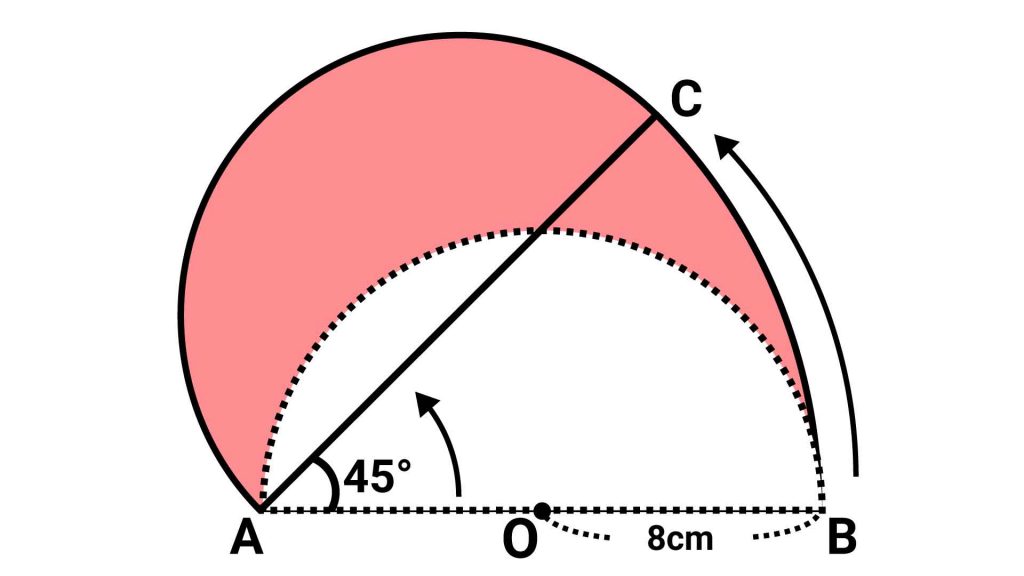
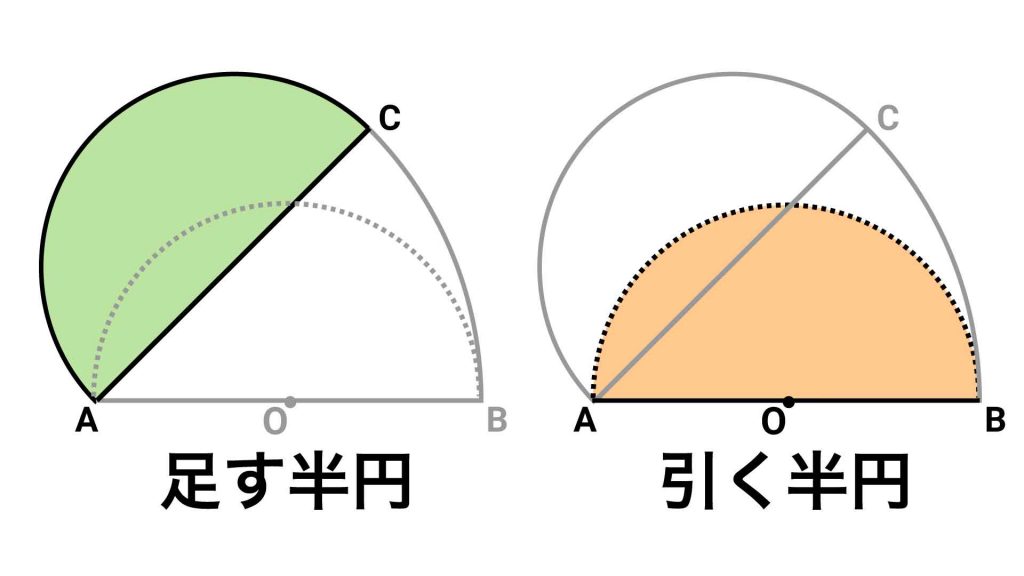
半円の面積を足し引きする
おうぎ形の面積がわかりましたので、左上にある半円の面積を足し、赤く塗られていない半円部分の面積を引けば、目的の図形の面積を求めることができます。
今から面積を足し引きしようとしている2つの半円を見てください。緑色の半円は、黄色の半円を動かしたものなので、どちらも半径は8cmです。つまり、この2つの半円は合同で、同じ面積をもっているのです。
これにより、半円同士の面積の足し引きは±0になります。したがって、目的の図形の面積は、半径16cm中心角45度のおうぎ形と等しいということがわかります。
以上により、求めたい図形の面積は、先ほど計算したおうぎ形の面積と同じく、32πcm2となります。
答え:32πcm2
またの挑戦をお待ちしています!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









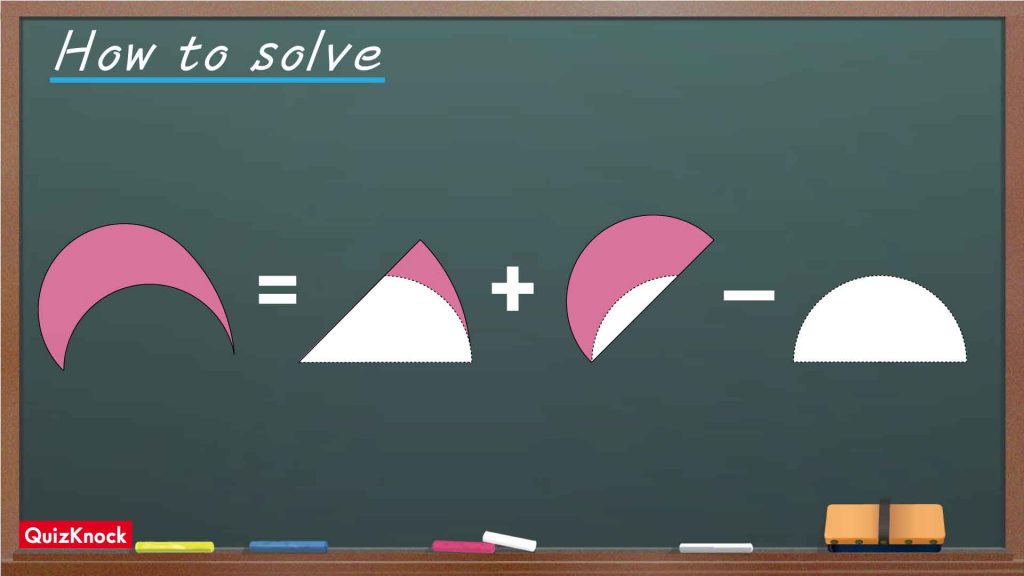
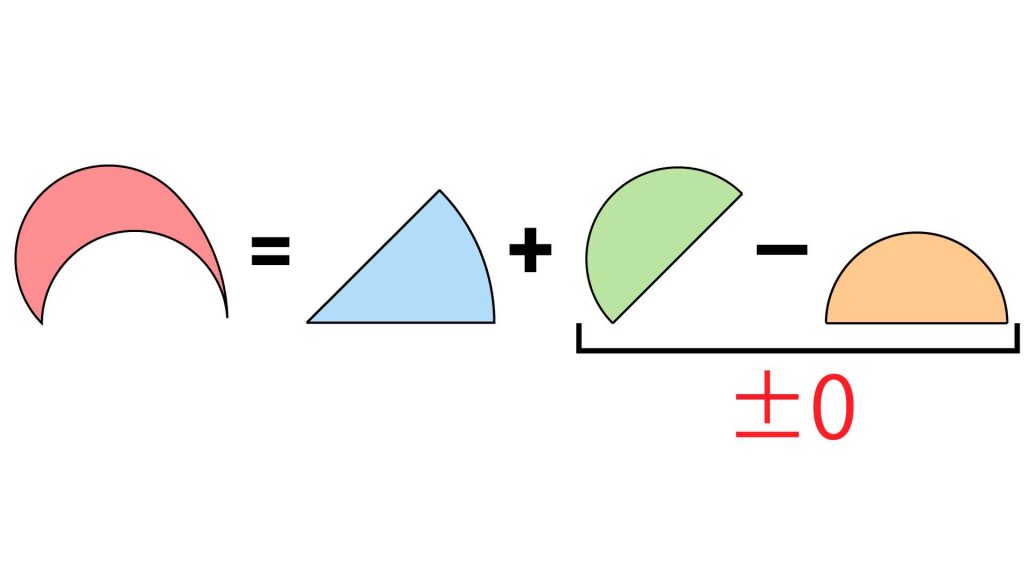
.jpg)










.jpg)






