解説
それでは解説です。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
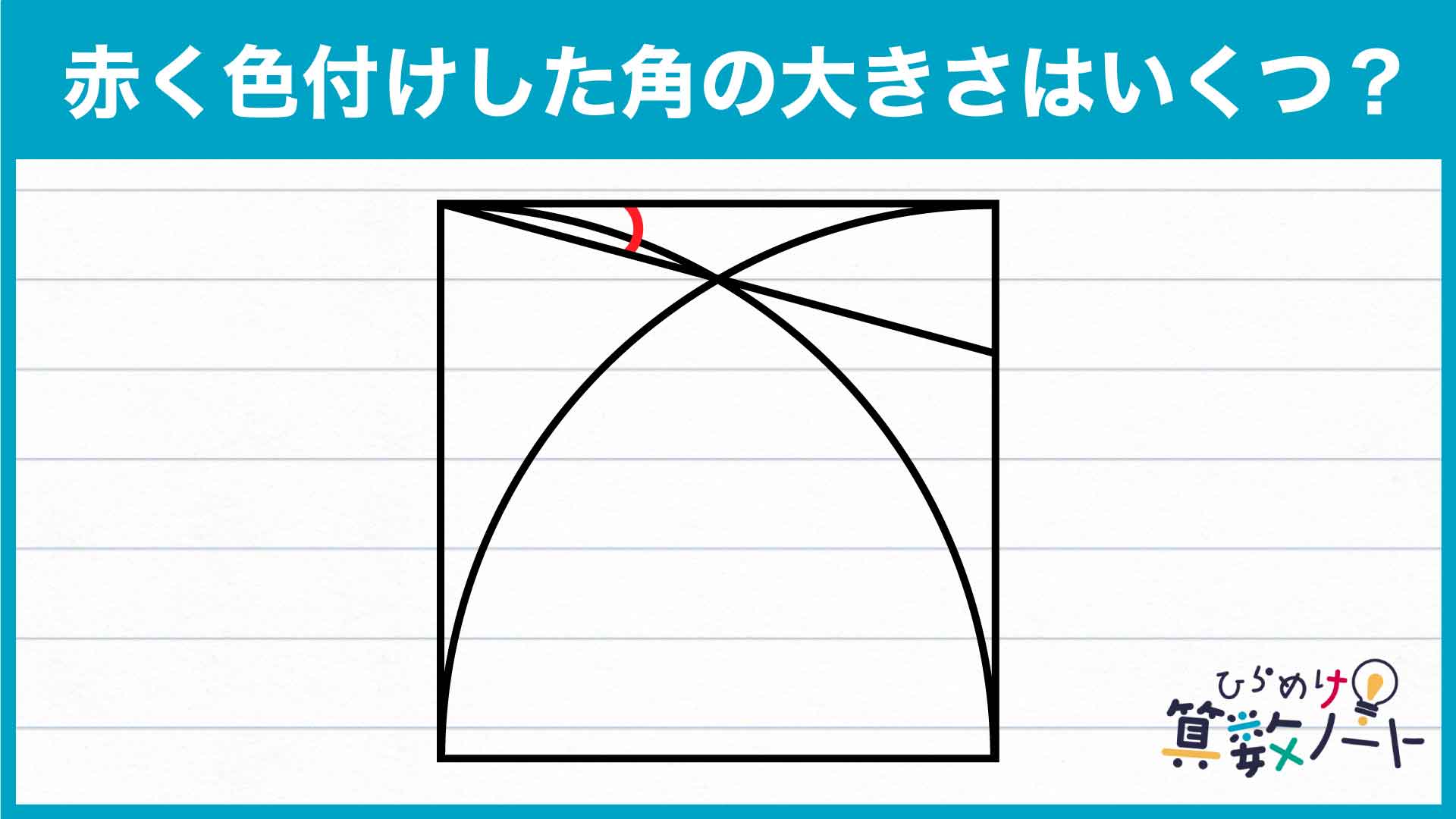
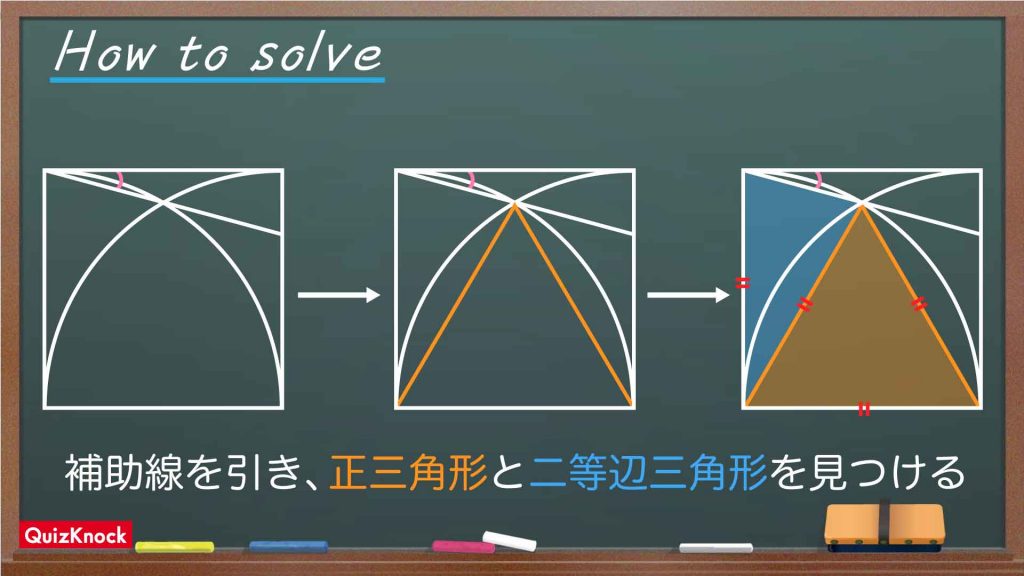
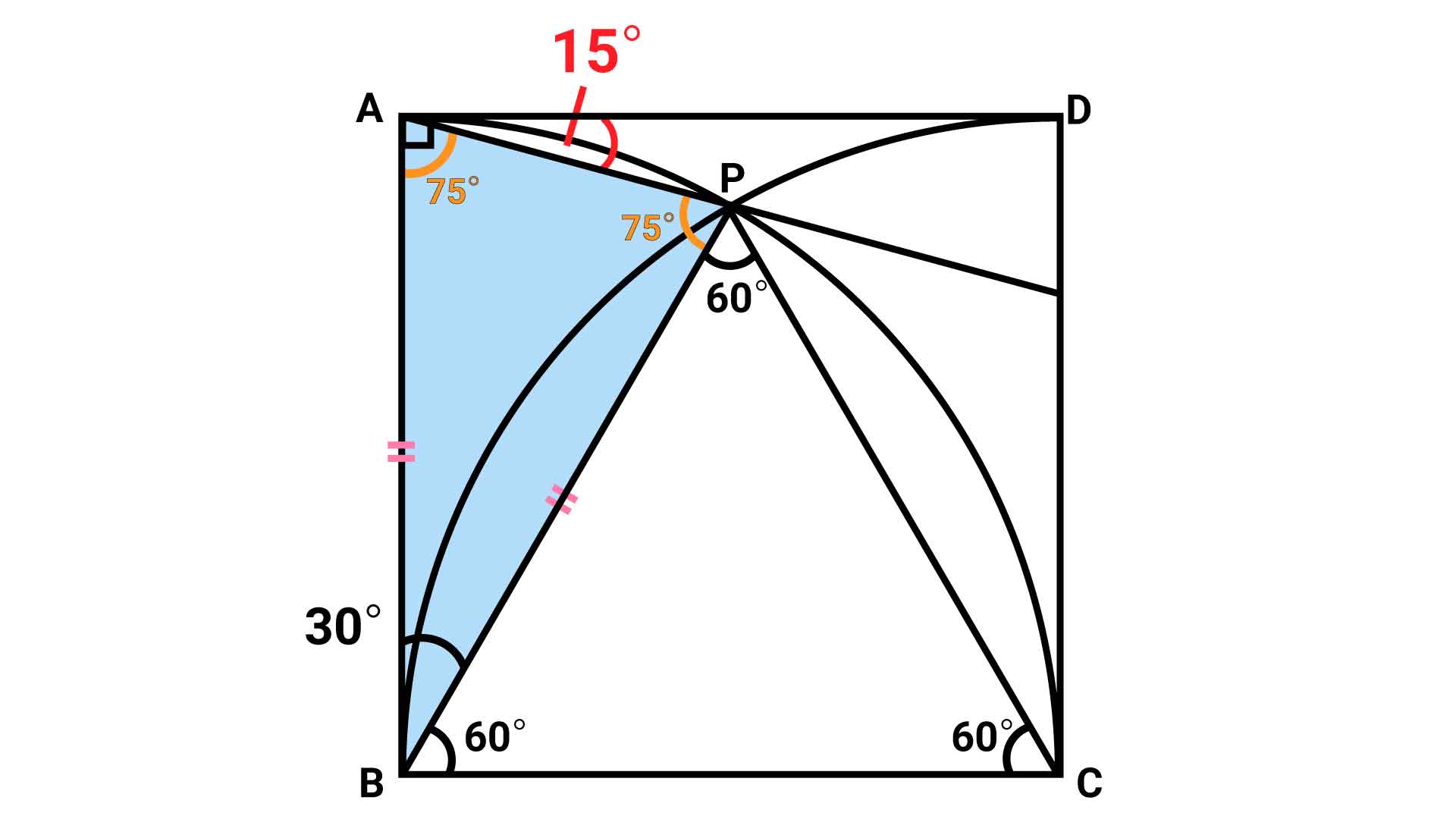
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引き、正三角形と二等辺三角形をを見つけることです。
この図の流れに沿って、順に解いていきましょう!
補助線を引き、正三角形を見つける
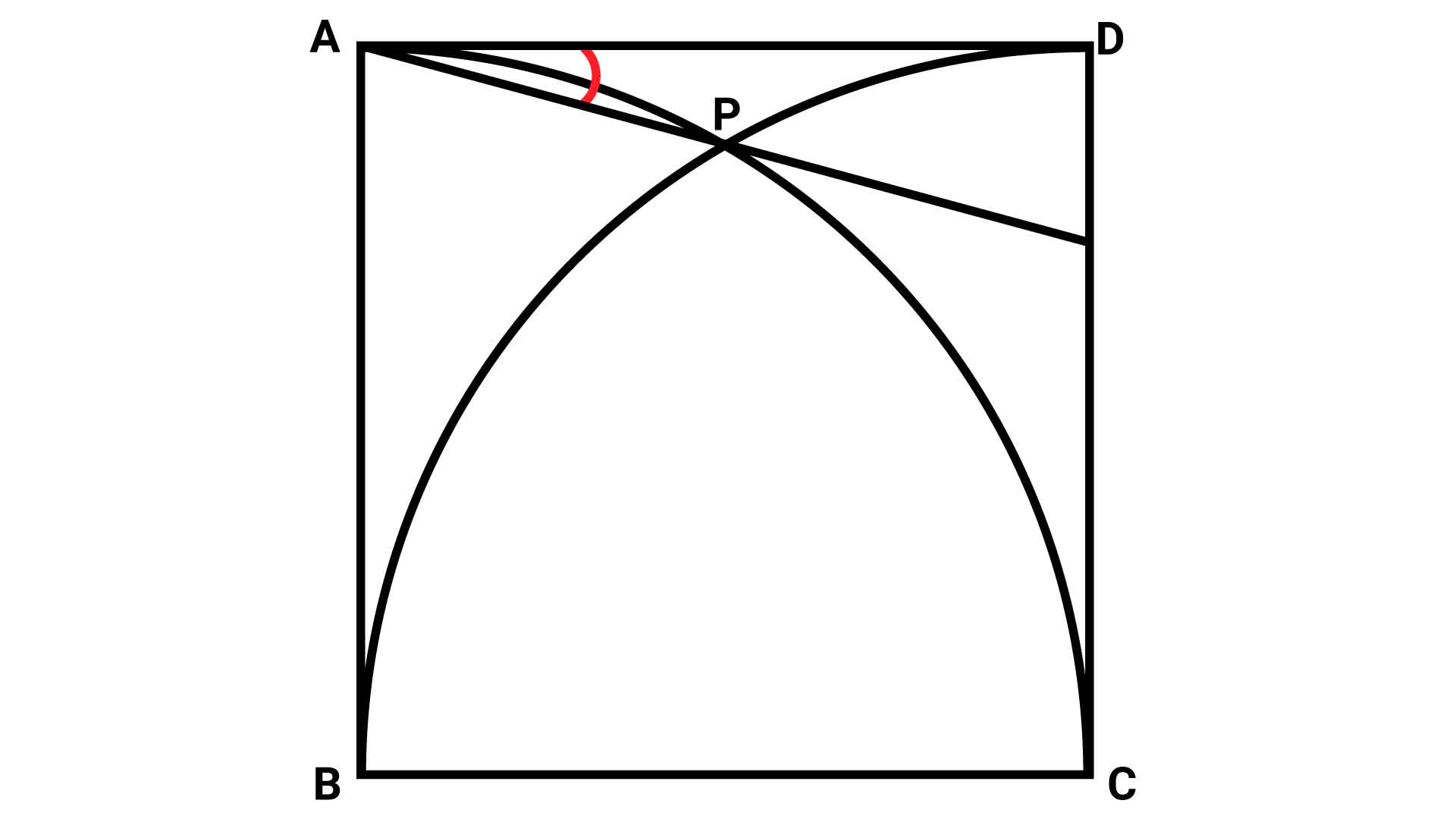
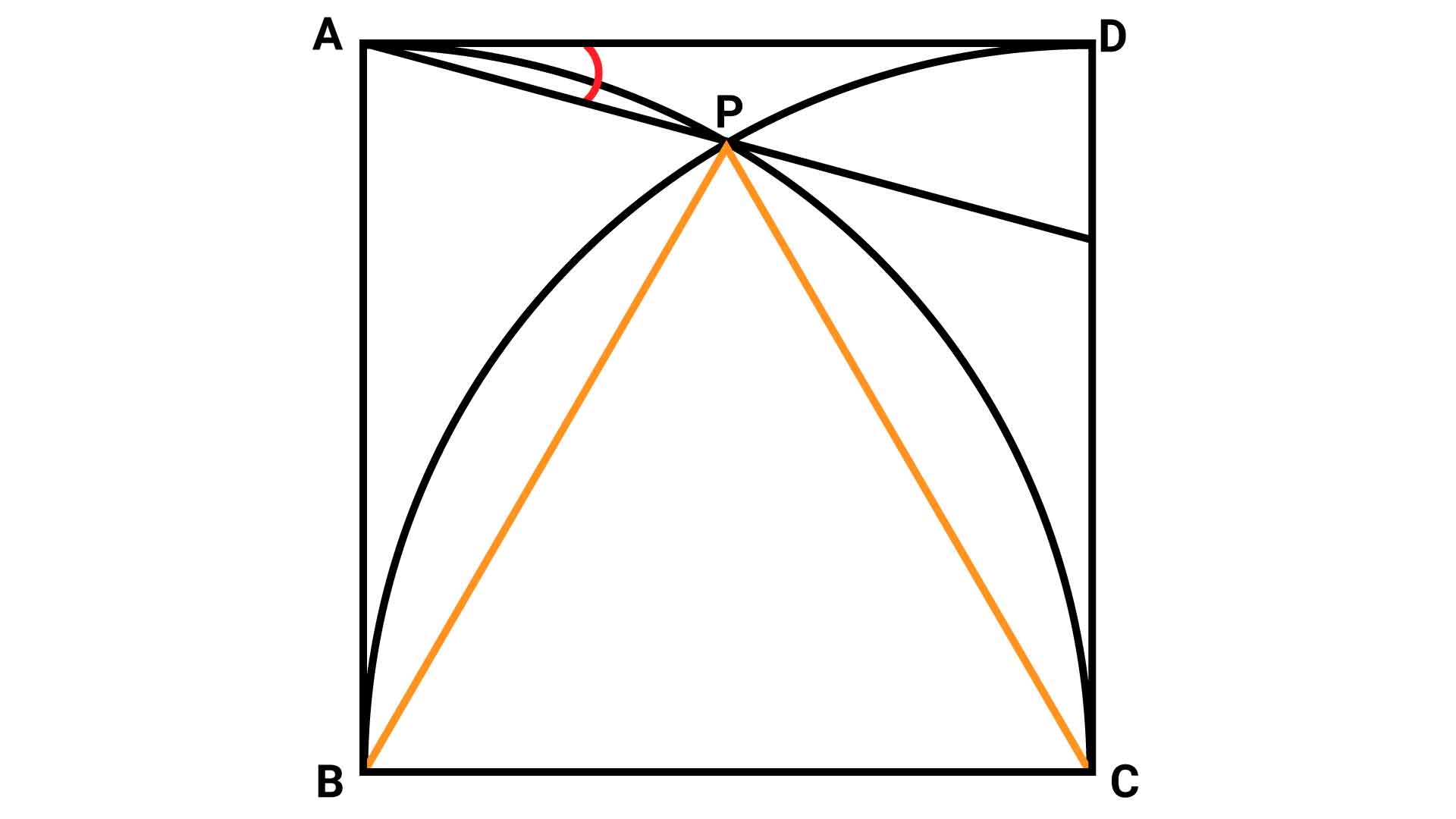
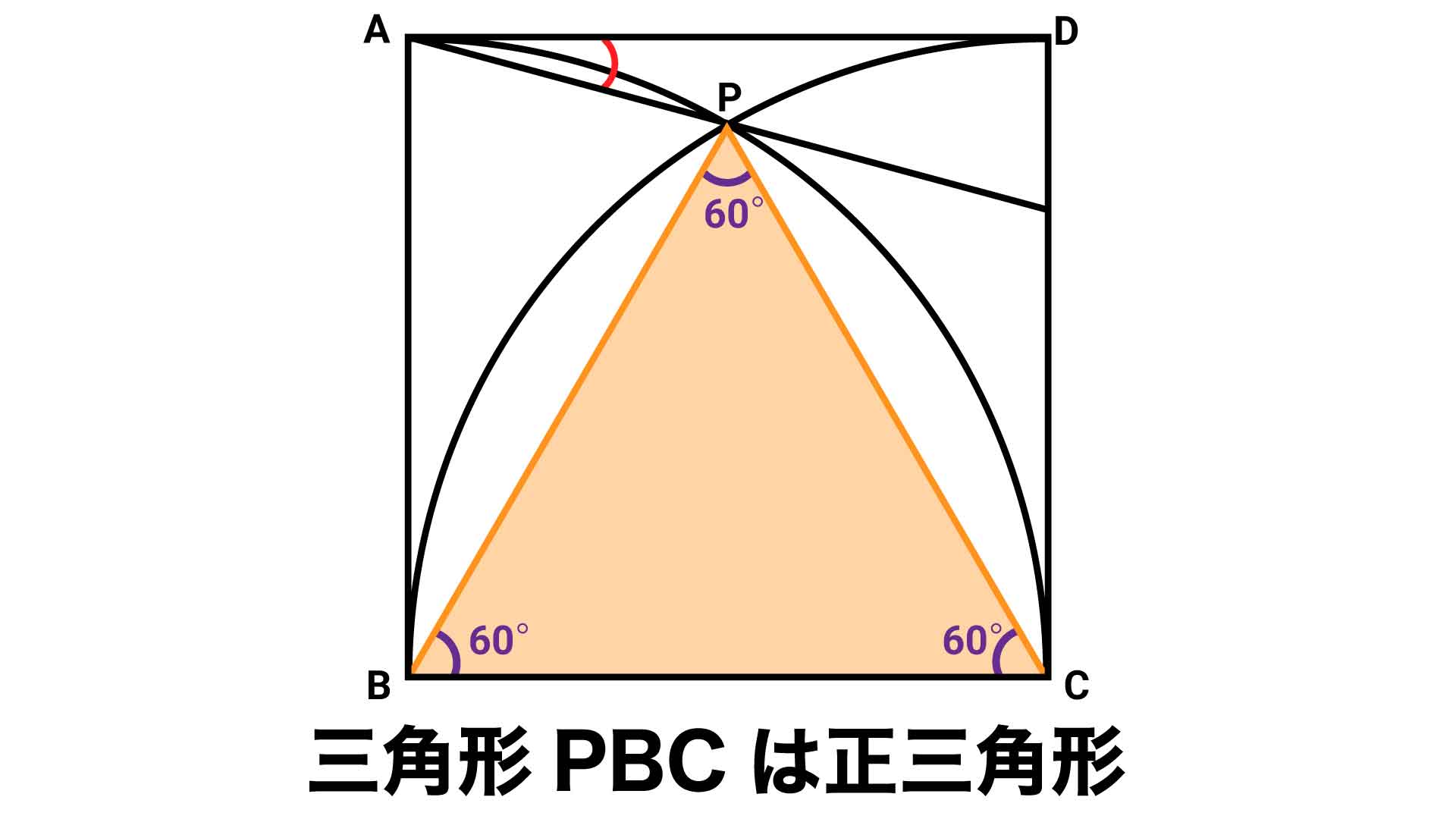
まず、以下の図のように、それぞれ点Bと点P、点Cと点Pを結ぶ補助線を引きます。
ここで、点Bを中心とする扇形に着目すると、BCとBPはこの扇形の半径であるため、長さは等しくなります。
同様に、点Cを中心とする扇形に着目すると、BCとPCはこの扇形の半径であるため、長さは等しくなります。
以上より、BC、BP、PCが全て同じ長さなので、三角形PBCは正三角形であることがわかります。正三角形の内角の大きさはそれぞれ60度であるため、角PBC=60度です。
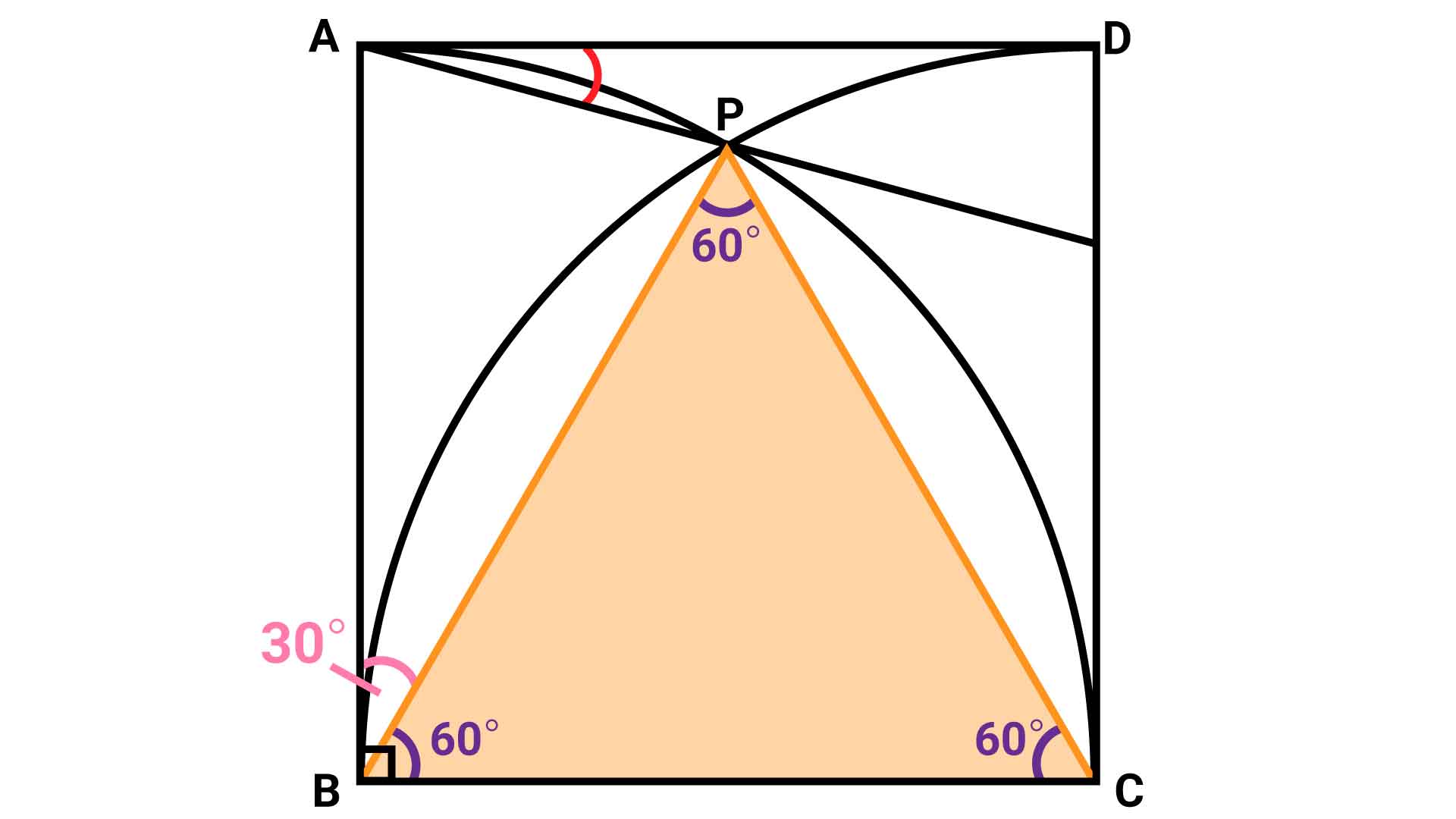
角PBCの大きさがわかると、角ABPの大きさもすぐに求めることができます。角ABCは正方形の内角のひとつであるため、90度です。このことから、角ABP=90-60=30度となります。
三角形ABPに注目する
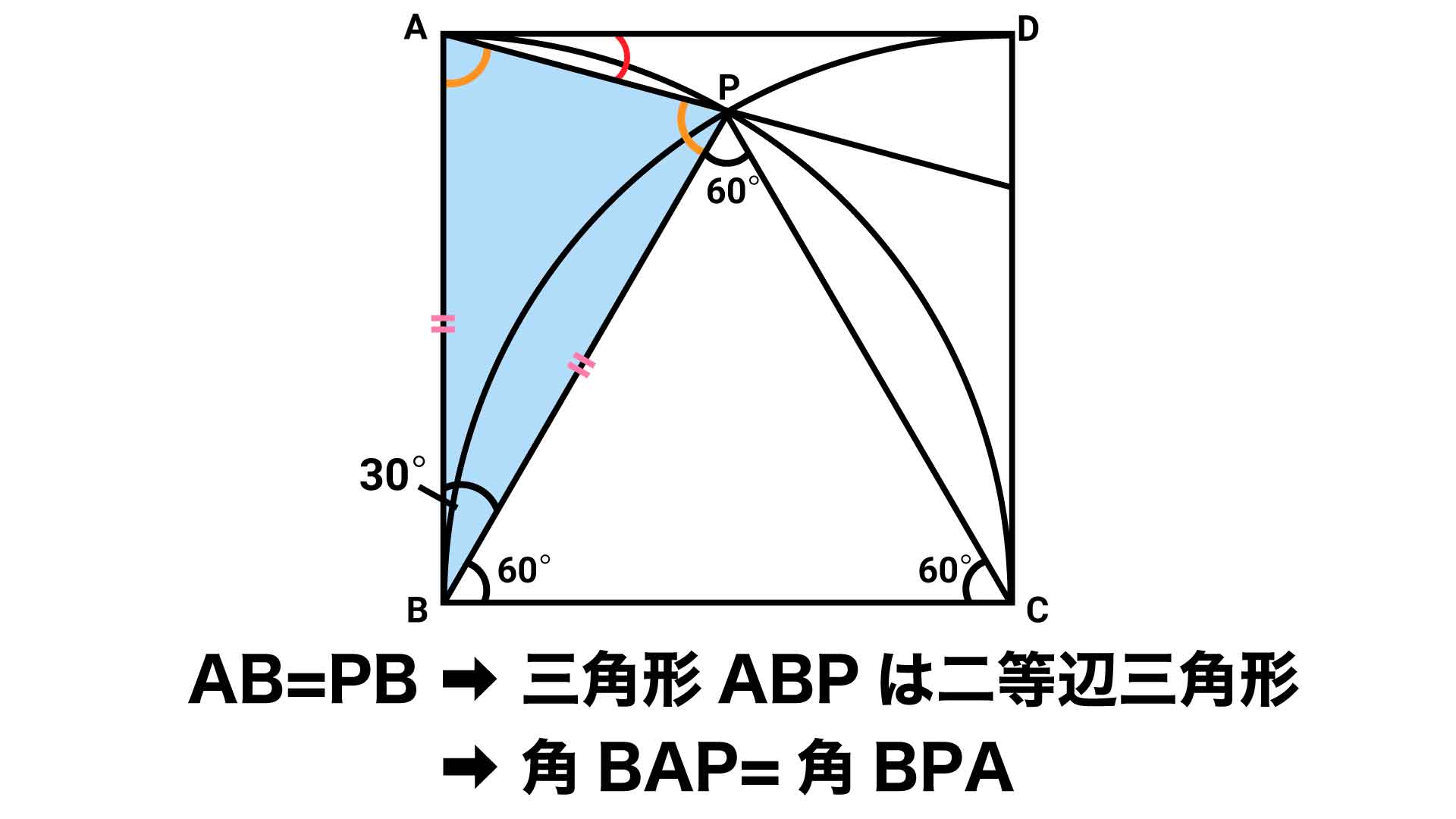
次に、三角形ABPに注目します。
点Bを中心とする扇形に着目すると、ABとPBはこの扇形の半径であるため、長さは等しくなります。
これにより、三角形ABPは、辺AB=辺PBの二等辺三角形であることがわかります。したがって、角BAP=角BPAとなります。
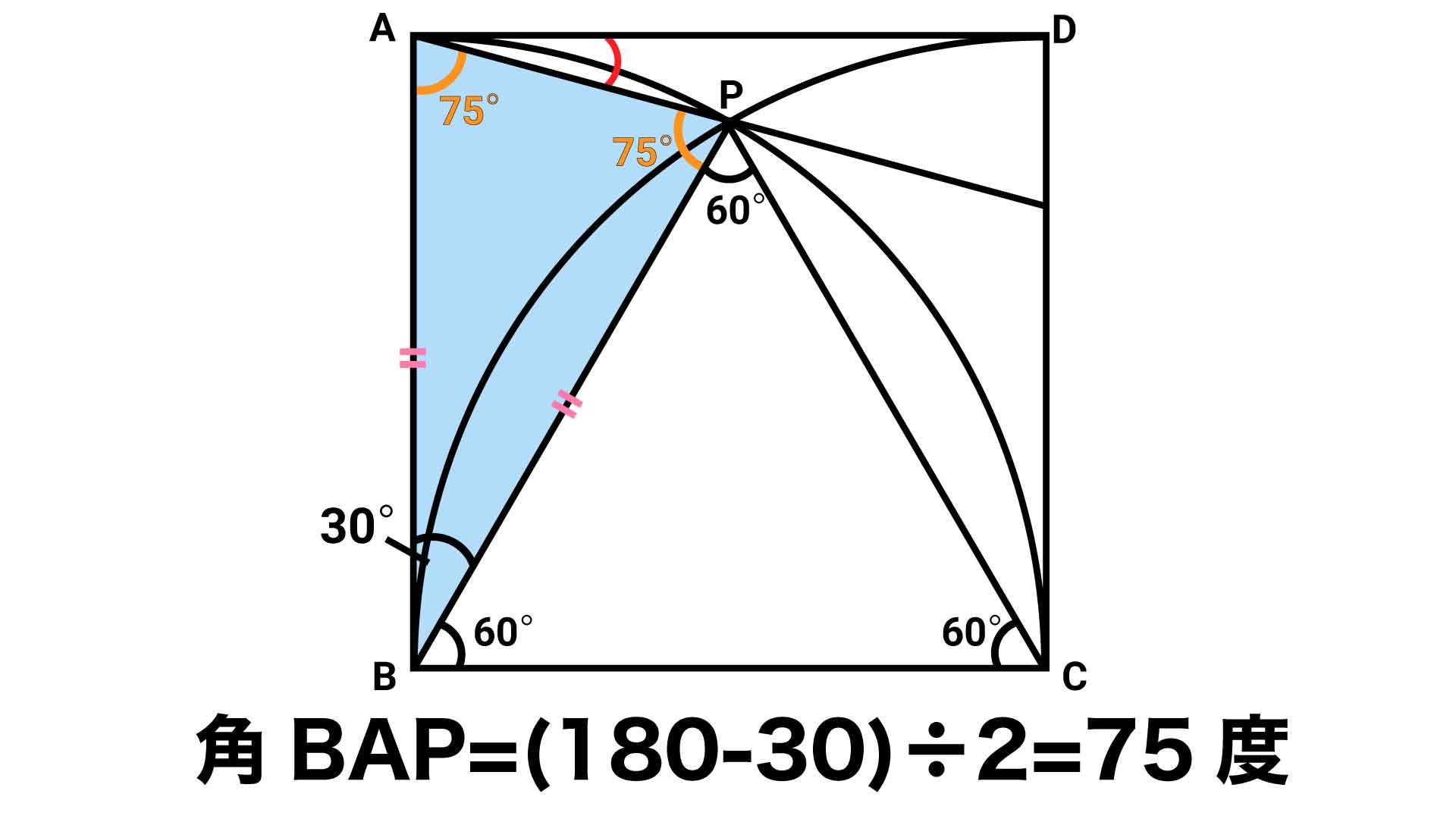
三角形の内角の和が180度であることと、角ABP=30度であることから、角BAP=(180-30)÷2=75度となります。
あと一歩!
角BADは、正方形の内角のひとつであるため90度で、角DAPと角BAPを足し合わせたものです。
したがって、求めたい角DAPの大きさは、90-75=15度となります。
答え:15度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)










.jpg)





