解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここではそのうちのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
今回のポイントは、次の2つです。
- Aの候補を絞りこむ
- A=1を起点にして計算する
どういうことなのか、順を追って説明していきます。
大きい位に注目する
Aに入る数字の候補は1~9まであるため、しらみつぶしに当てはめるのは面倒です。なので、事前にある程度候補を絞っておくと、後々計算が楽になります。
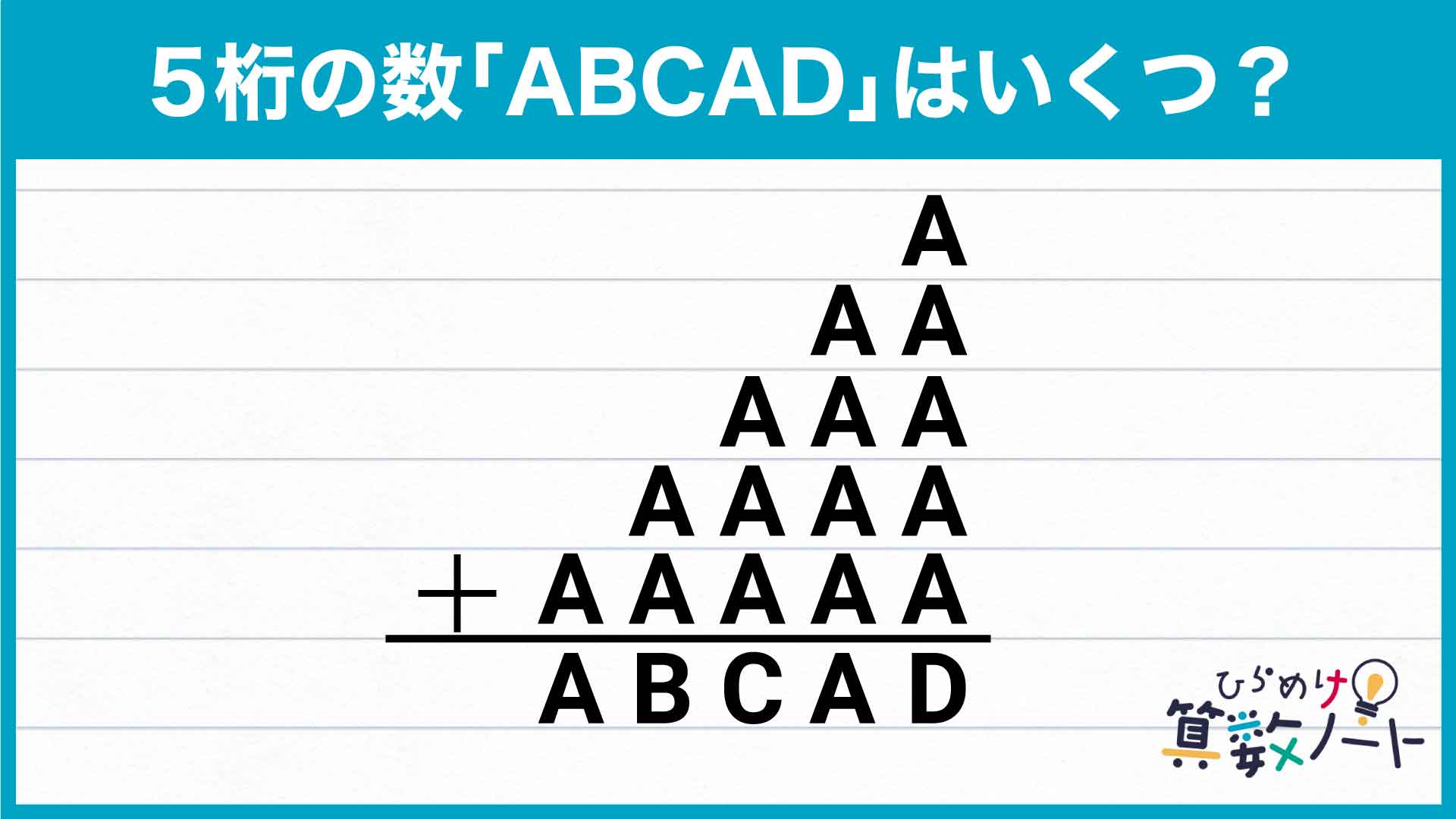
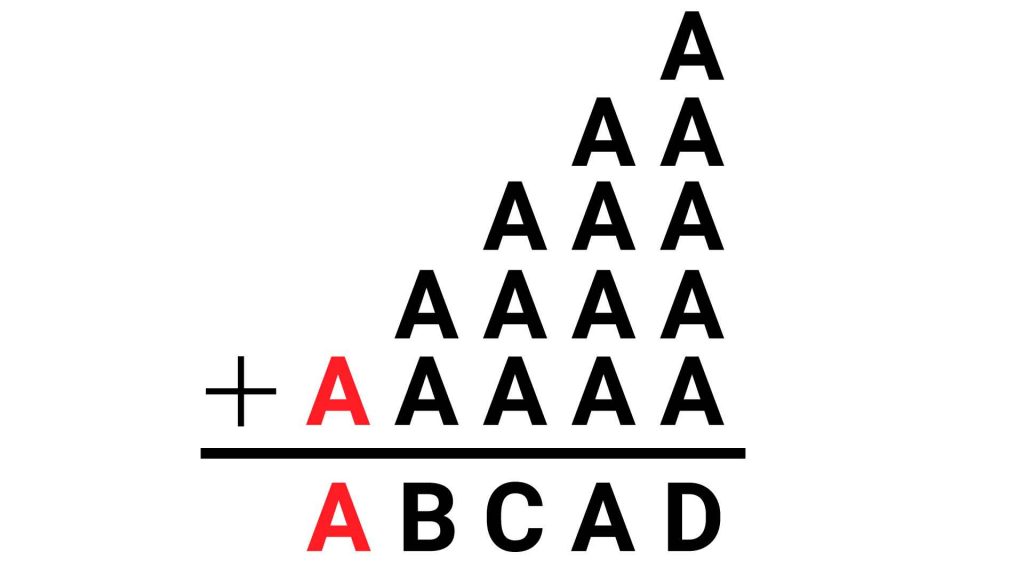
そこで、まず最も左にある一万の位を見てください。
一見、「A=Aなんだから当たり前じゃん!」と思うかもしれません。しかしよく見ると、ここにAの候補を半分以下に減らす重要な情報が含まれています。
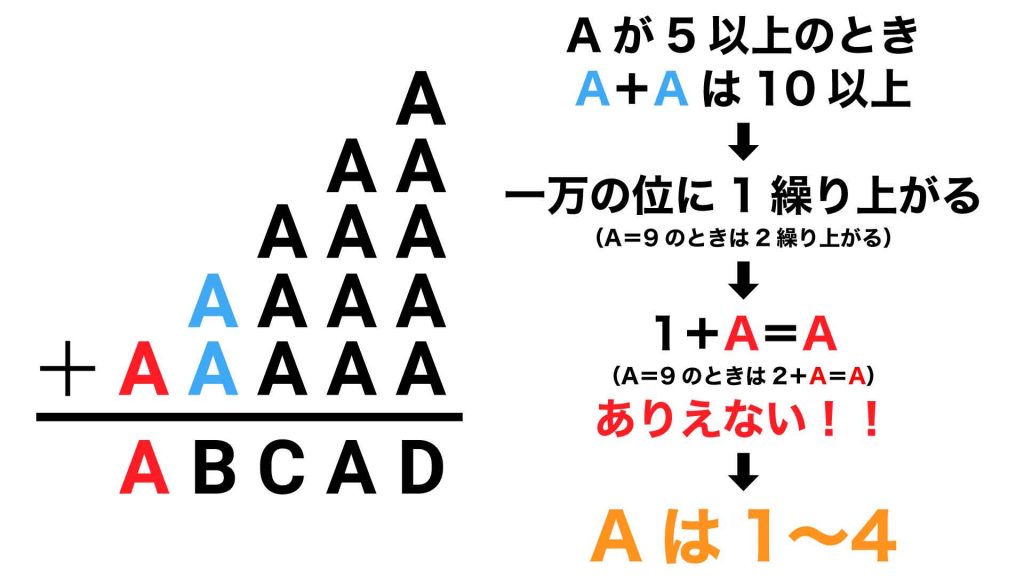
そう、千の位からの「くり上がり」がないのです。
もし、千の位にある「A+A」という計算の答えが10以上だった場合、一万の位はA+1=AまたはA+2=Aというありえない式になってしまいます。
つまり、一万の位で「A=A」が成り立つということは、Aが5未満(1~4)であることを意味しているのです。
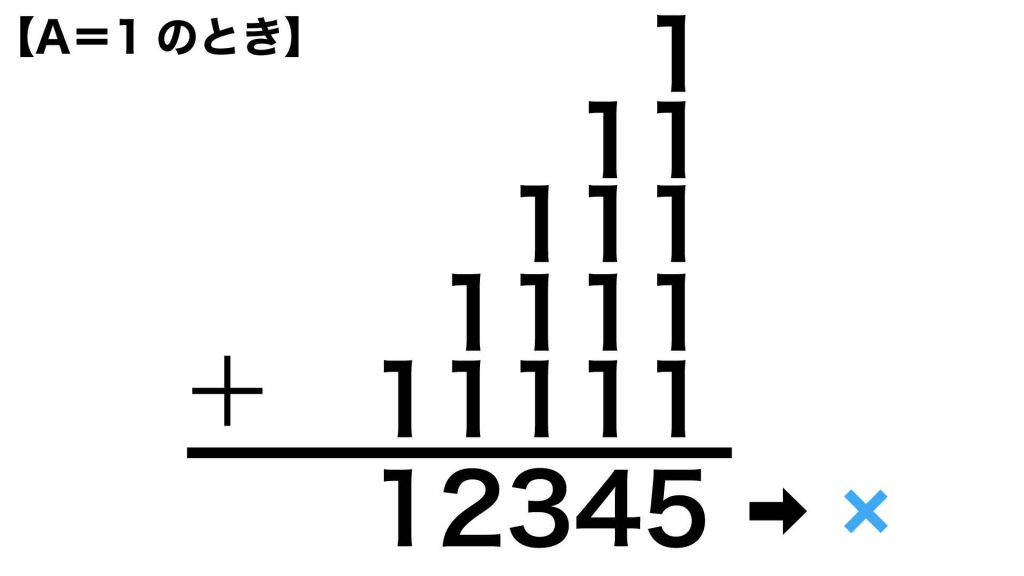
A=1だった場合の答えを活用する
Aの候補が1~4に絞られたところで、手始めにAに1をあてはめてみましょう。
筆算の答えは「12345」と簡単に求められます。これは「ABCAD」にこそ当てはまりませんが、解答を素早く導き出すための大きなヒントになります。
A=2のとき、足し算に使われる全ての数が、A=1だったときの2倍になります。つまり、筆算の答えも2倍になり、A=2のときの答えは12345×2と求められます。同様に、A=3のときは12345×3、A=4のときは12345×4と求めることができます。
これらの3つの式のなかから、答えが「ABCAD」に当てはまるパターンを見つければよいのです。かけ算にまとめてしまえば、逐一足し算をするよりも計算間違いが起こりにくくなります。
上の計算式から、「ABCAD」のパターンに合致するのはA=3の場合の「37035」だとわかります。
答え:37035
またの挑戦をお待ちしています!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







