解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。
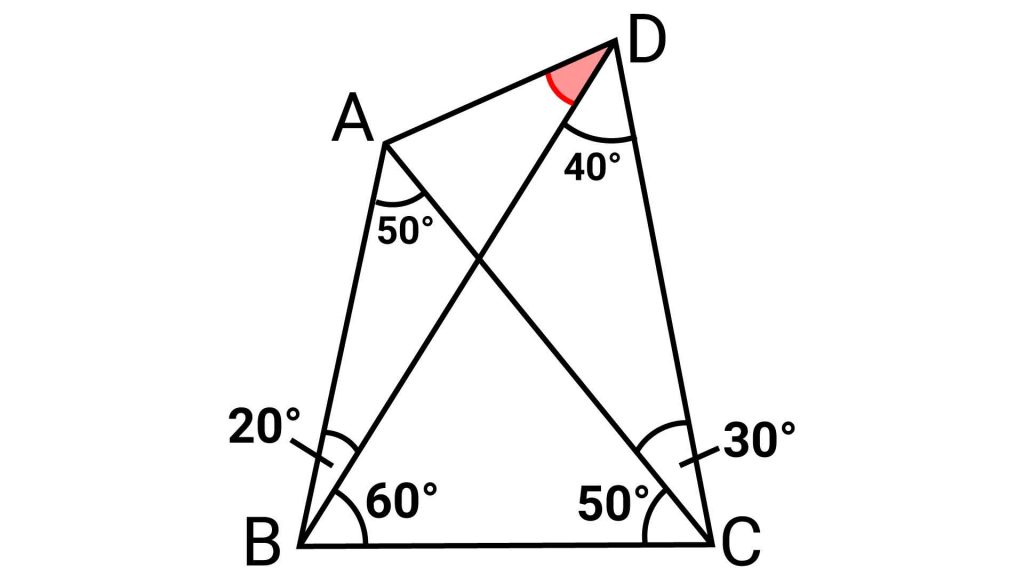▲わかっている角度が多く、簡単そうに見えますが、一筋縄ではいかない激ムズ問題です
なかなか根気のいる作業なので、僕と一緒に解いていきましょう！
いったん、ゴールから逆算して考えてみます。
三角形ACDにおいて、下の図で赤く色付けした2つの角度のどちらかがわかれば、三角形の内角の和が180度であることを用いて、芋づる式に答えが出てきます。
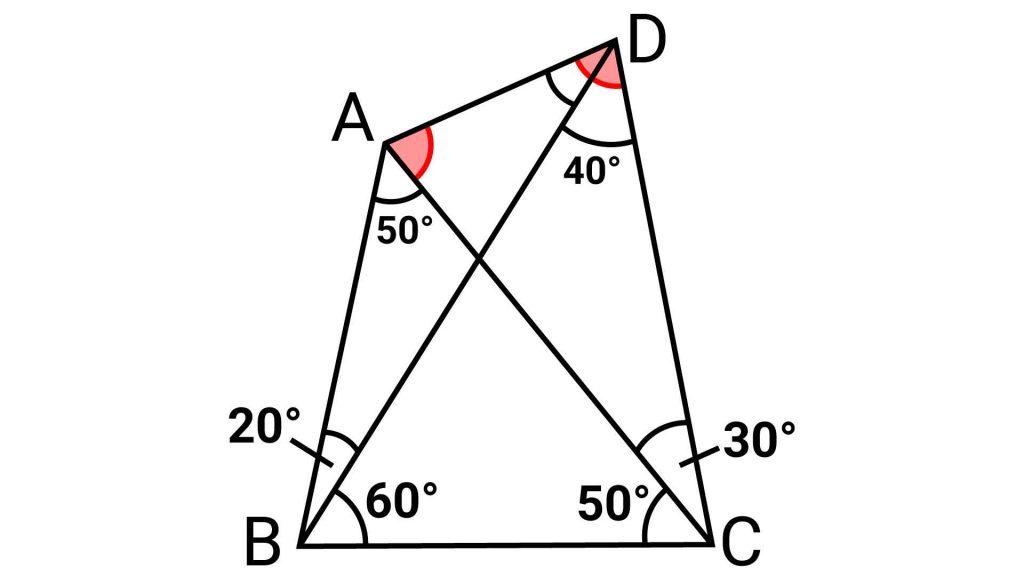▲赤く色付けした角度のどちらかがわかれば、角ADBの大きさがわかる。
この角度を求めるために数ステップ必要になるのですが、解きやすくするために補助線を引きます。
補助線の引き方が、この問題の最大のポイントです！
ヒントとなった補助線はこちら！
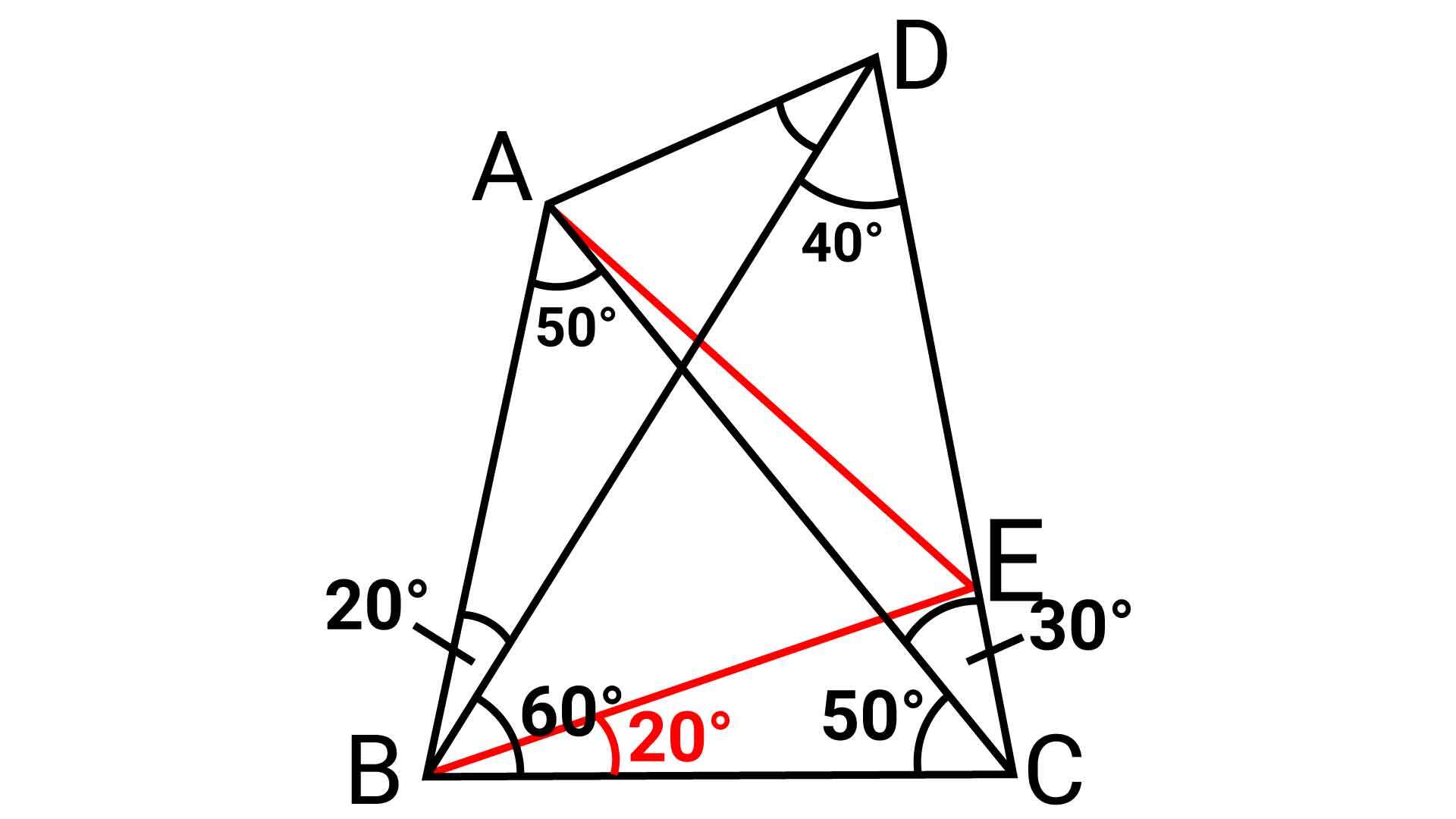
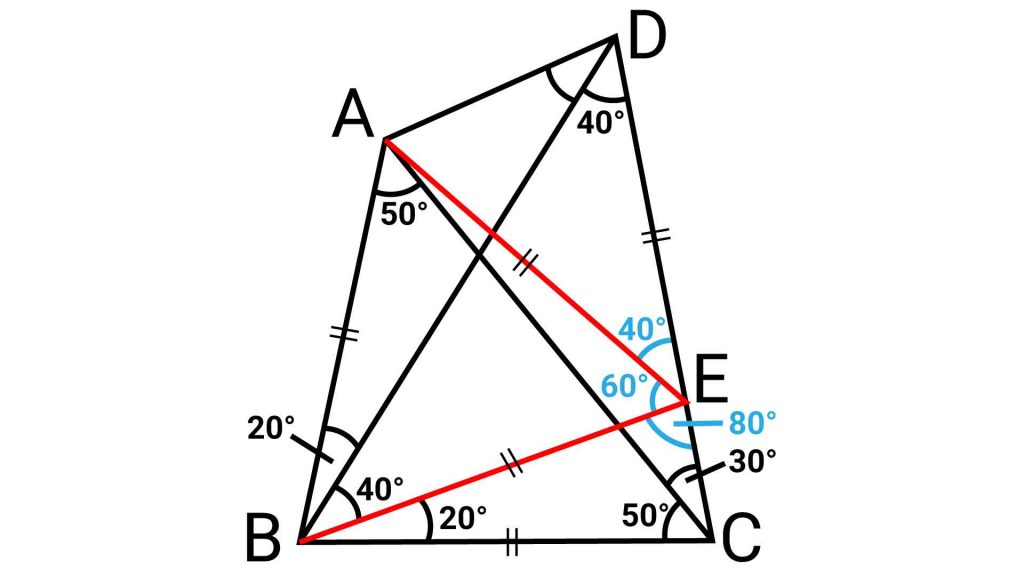
下の図の赤い2本の線が、解くのに必要な補助線です。
【1本目】辺CD上に、角EBC=20度となる点Eをとり、EとBを結ぶ
【2本目】AとEを結ぶ
▲思いつくだけでもスゴい、2本の補助線
かなりトリッキーな引き方ですね……。
ねらいは「二等辺三角形をつくること」です。角BCDは80度であることがわかっているため、1つの角が20度になるように補助線を引けば、残りの角度は80度となり、三角形BCEを二等辺三角形にすることができるのです。
しかもうれしいことに、この2本の補助線を引くことで二等辺三角形が大量にできます。
天下り的に補助線が登場してやや気持ち悪さを感じるかもしれませんが、これから説明する解法を見れば、とても合理的に引かれている線であることがわかります。
この図からスタートして、順に解いていきましょう！
ステップ1：1つ目の二等辺三角形ABC
ここでは、まず補助線は使わなくてもわかることを把握しておきます。
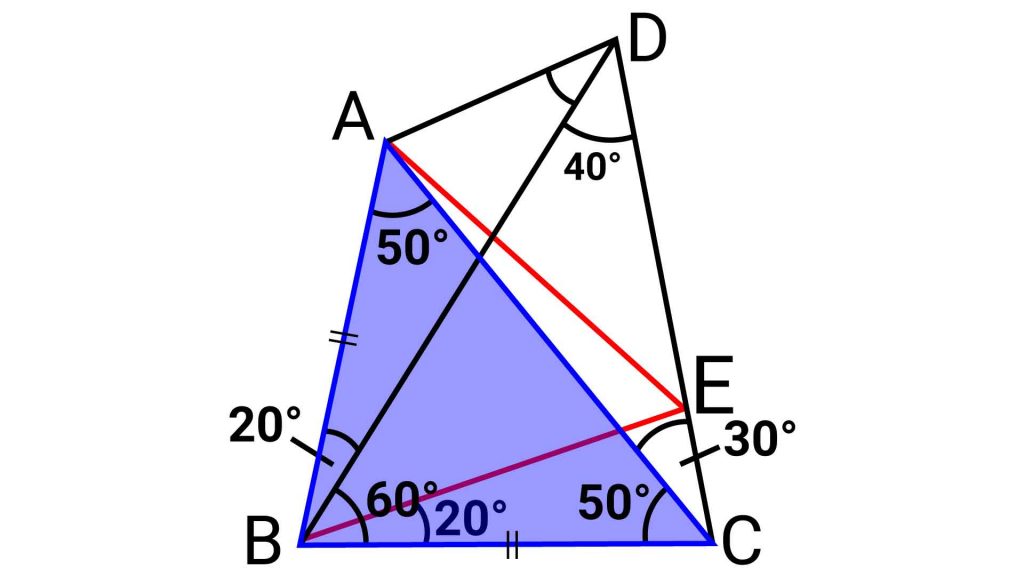
まず、三角形ABCに着目します。
角BAC=角BCA=50度なので、三角形ABCは二等辺三角形となり、BA=BCです。
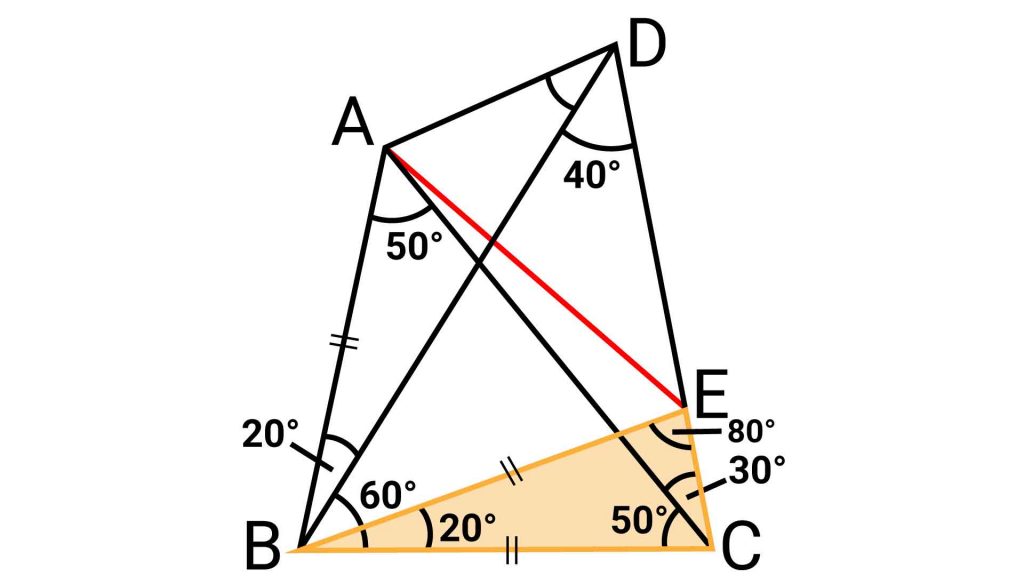
ステップ2：2つ目の二等辺三角形BCE
次に、三角形BCEに着目します。
補助線を引くときに紹介したように、角EBC=20度、角BCE=80度なので、角BEC=80度であることから、三角形BCEは二等辺三角形となり、BC=BEです。
ステップ1の結論であるBA=BCと合わせると、BA=BEとなります。
ちょっとだけ図が複雑になりました。
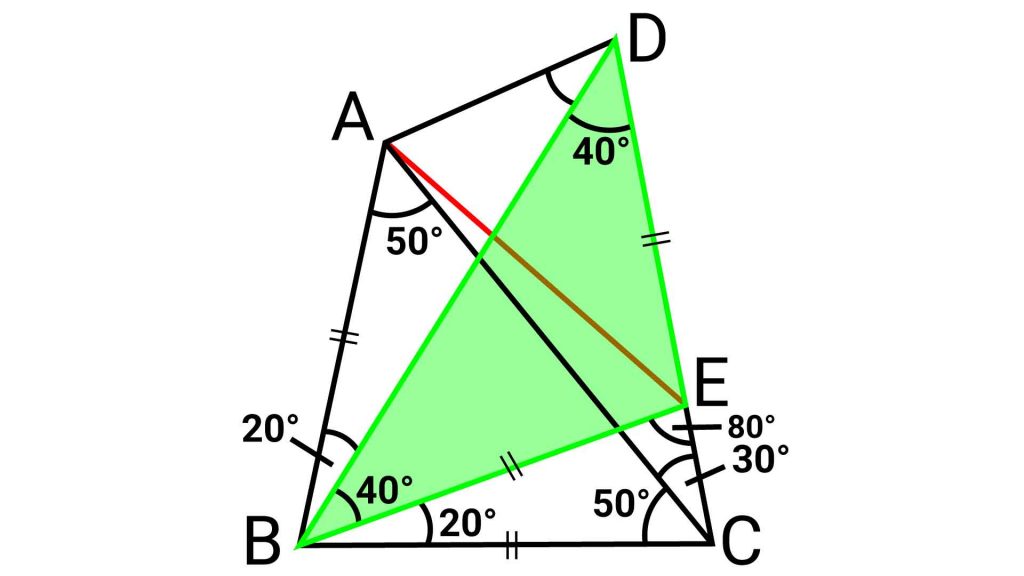
ステップ3：3つ目の二等辺三角形EBD
次に、三角形DBEに着目します。
角DBC=60度、角EBC=20度なので、角DBE=40度です。
また角BDE=40度なので、三角形EBDは二等辺三角形となり、EB=EDです。
この三角形、埋もれていて見つけづらい……!
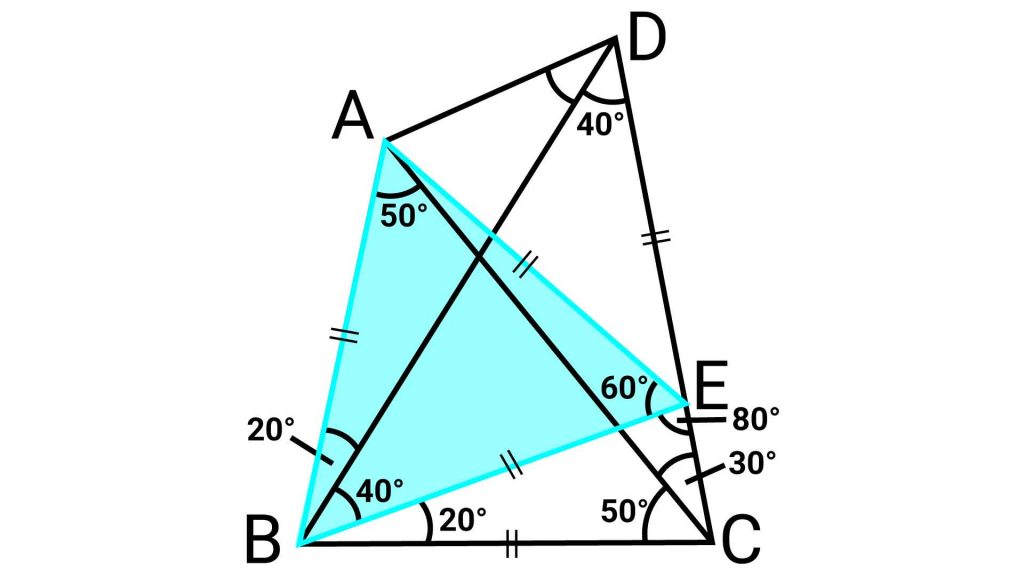
ステップ4：4つ目の三角形BAEは正三角形
次に、三角形BAEに着目します。
ステップ2の結論であるBA=BE、および角ABE=60度であることを踏まえると、三角形BAEは正三角形となり、BA=BE=EAです。
ステップ3の結論であるEB=EDと合わせると、ED=EAとなります。
したがって、三角形EADは二等辺三角形となり、角ADEと角DAEの大きさは等しいということになります。
最初に設定したゴールにかなり近づいてきました。そして図が複雑になるにつれ、図中の文字サイズがどんどん小さくなっていっています。
ステップ5：角DAEの大きさを求める
角ADEの大きさを求めるために、角AEDの大きさを求めます。
三角形ABEは正三角形なので、角AEB=60度です。また角BEC=80度なので、角AEDの大きさは、180-(60+80)=40度となります。
ステップ6：5つ目の二等辺三角形EAD
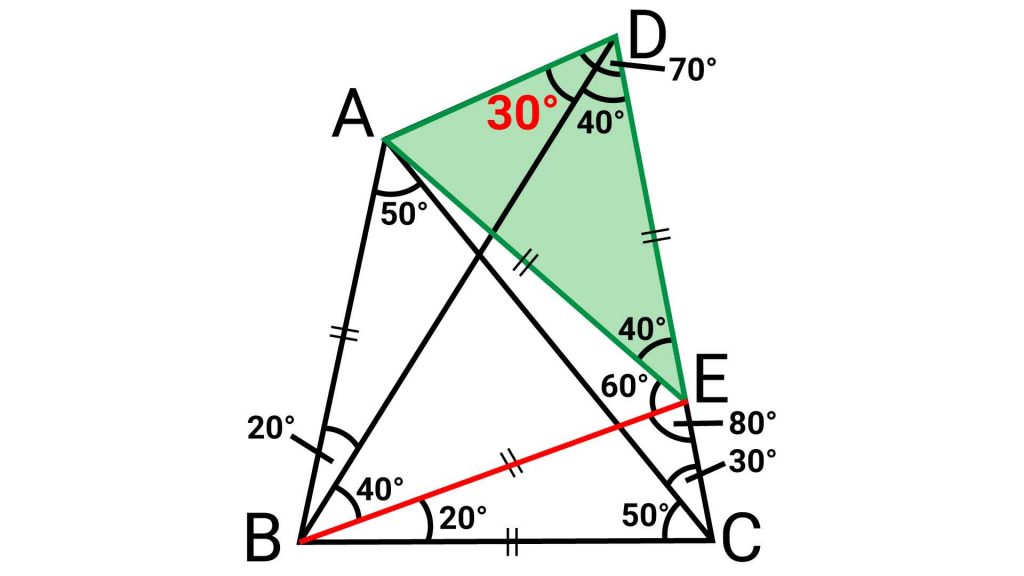
三角形EADが二等辺三角形で角AED=40度なので、角ADEと角DAEの大きさはそれぞれ(180-40)÷2=70度です。
角BDE=40度なので、求める角度ADBの大きさは、70-40=30度となります。
答え：30度
気づいたら本当に二等辺三角形がたくさんできてる！
最終的に、かなりごちゃついた図になりました。僕はこんなごちゃついた図を見るのが好きだったりします。ごちゃついた図って、なんかカッコよくないですか？
ここまでの長旅、大変お疲れさまでございました。
隠された二等辺三角形を地道に辿ることで、答えに辿り着くことができました。
補助線さえ思いついてしまえば、意外とスラスラと解けてしまいます。
まぁ、補助線を引くのが難しいのですが……。
「ラングレーの問題」には本当にさまざまな解き方が存在するので、ぜひ考えてみてください。
それでは。
【あわせて読みたい】
