小学5年生で解ける「図形の面積」の問題に挑戦！あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：自力で解きたい方はこちらへ！　以下は問題の解説です

今回の問題を解くうえで重要なポイントを以下にまとめました。

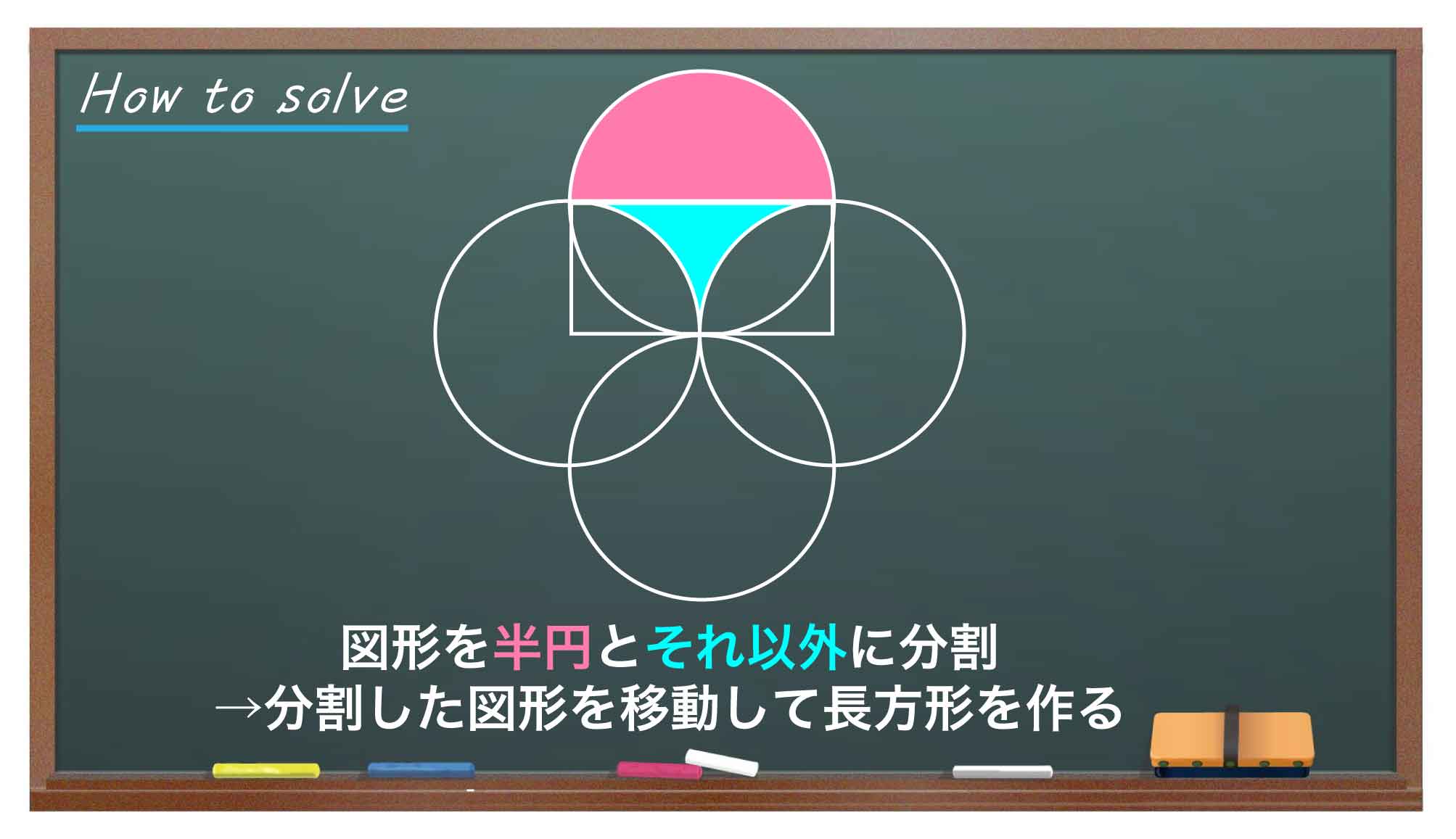
整理すると、

• 問題の図形の一部に注目し、その図形を「半円」と「それ以外の部分」に分割する
• 分割した図形をうまく移動させて、面積を求めやすい図形にする

の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。

図形を「半円」と「それ以外の部分」に分割する

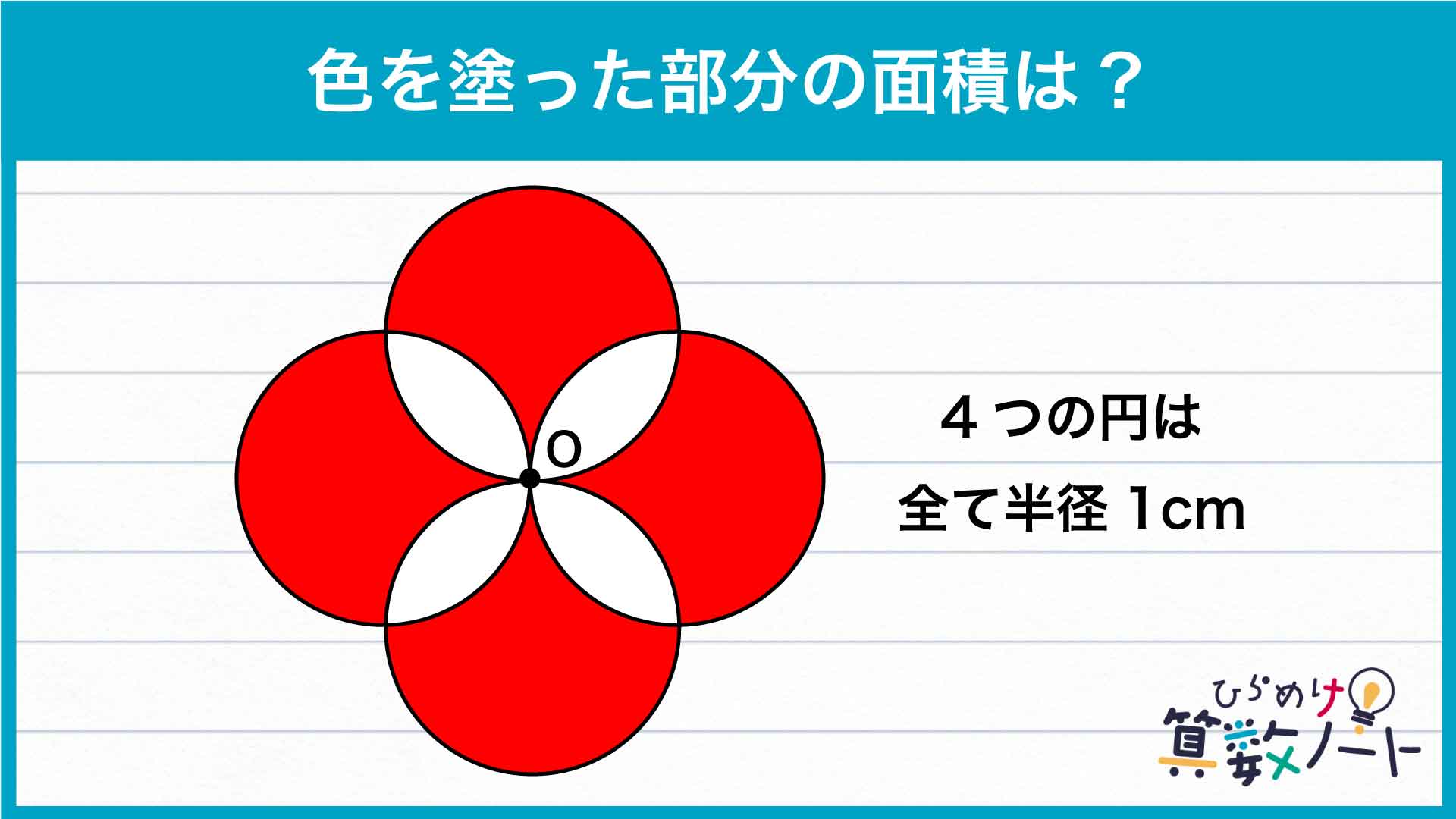
下の図ように、4つの円のうちの1つに注目してみます。

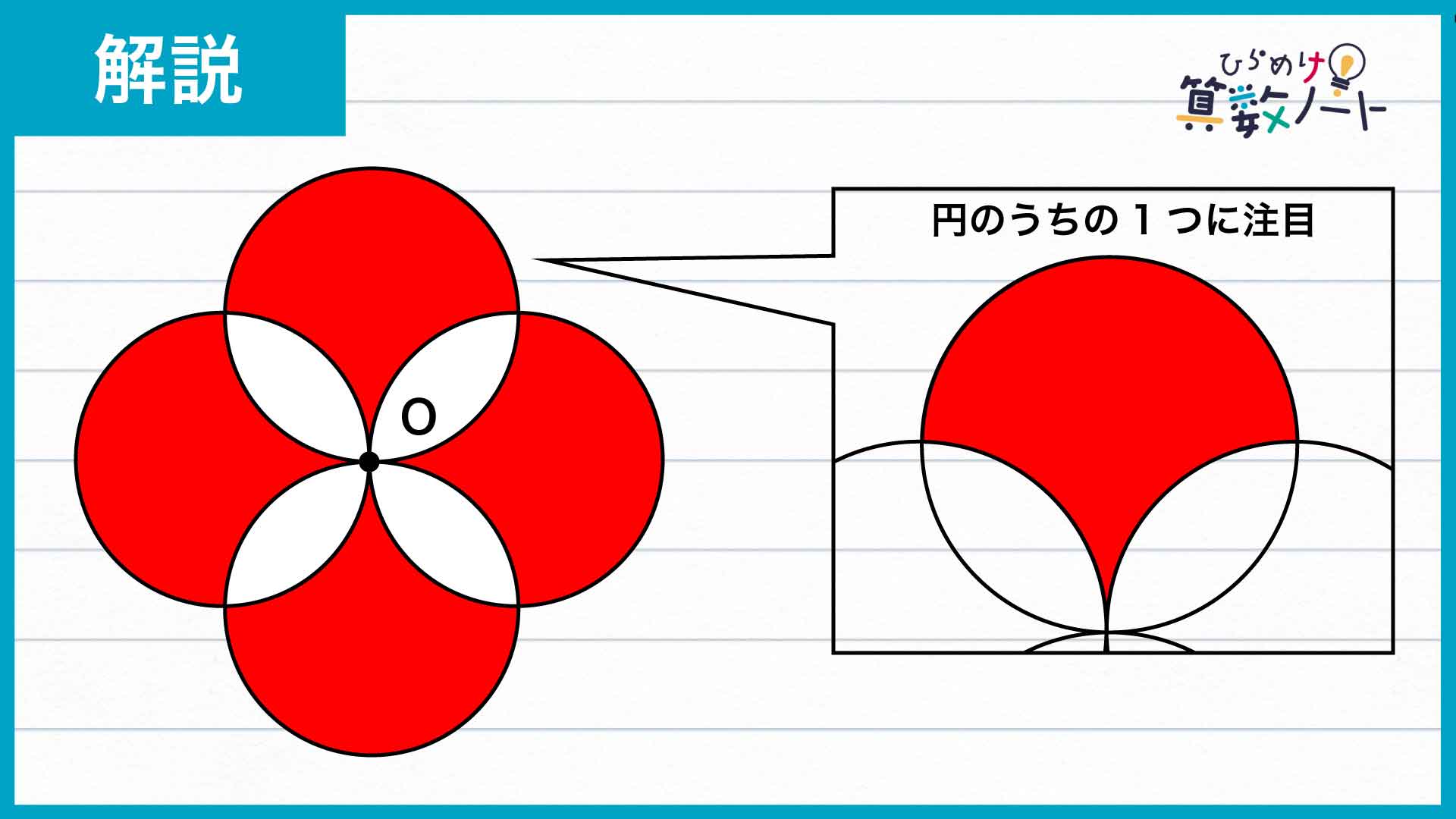
このとき、下の図のように、注目した円と他の円との交点をつなぐ補助線ADを引きます。補助線ADは注目した円の中心を通るため、図形を「円の半分（緑の部分）」と「それ以外の部分（青い部分）」に分割することができます。さらに、下の図のように長方形ABCDを書き加えます。

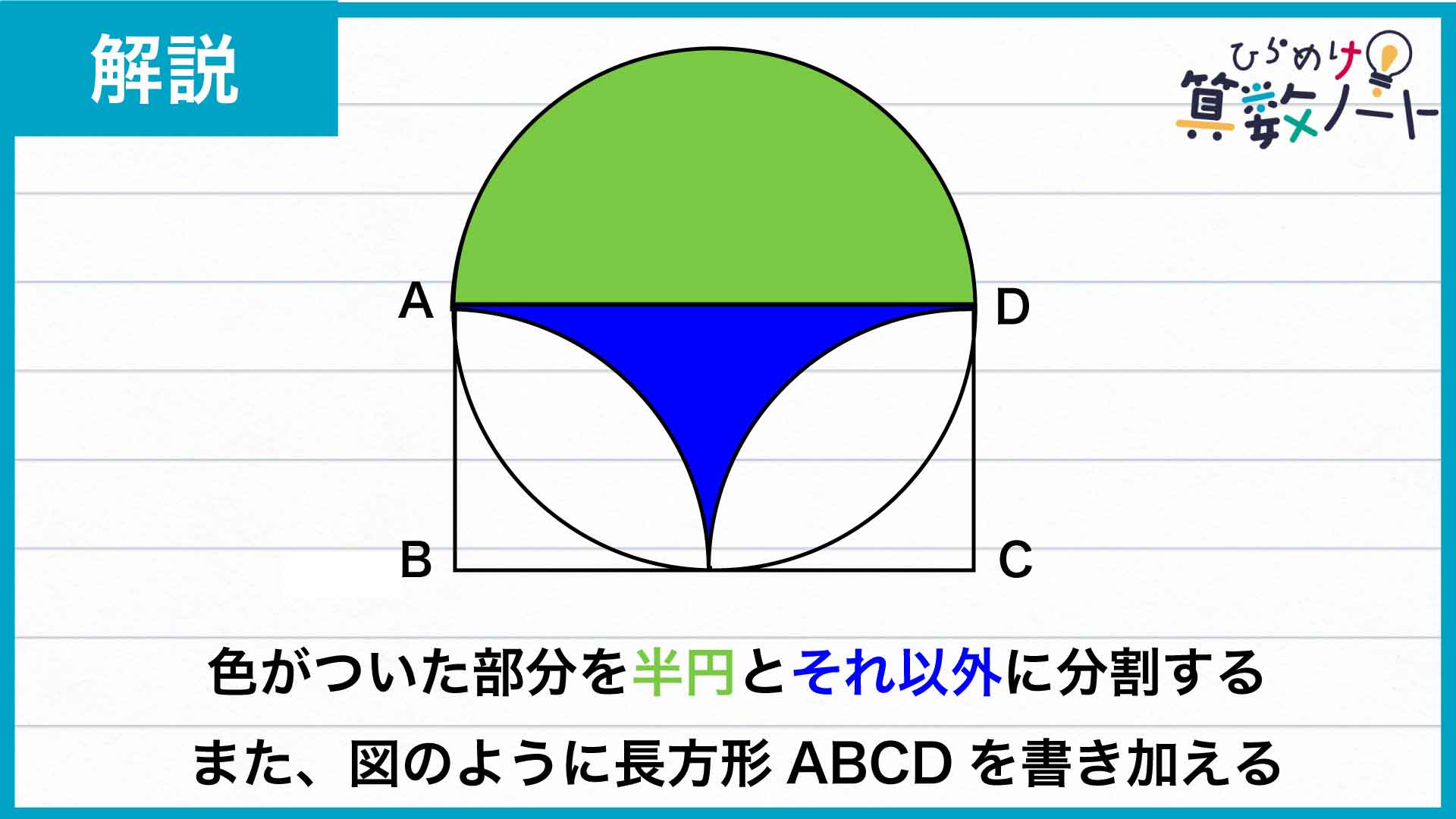
分割した図形を移動させる

ここで、青く色づけした部分に注目します。この部分を下の図のように移動させます。

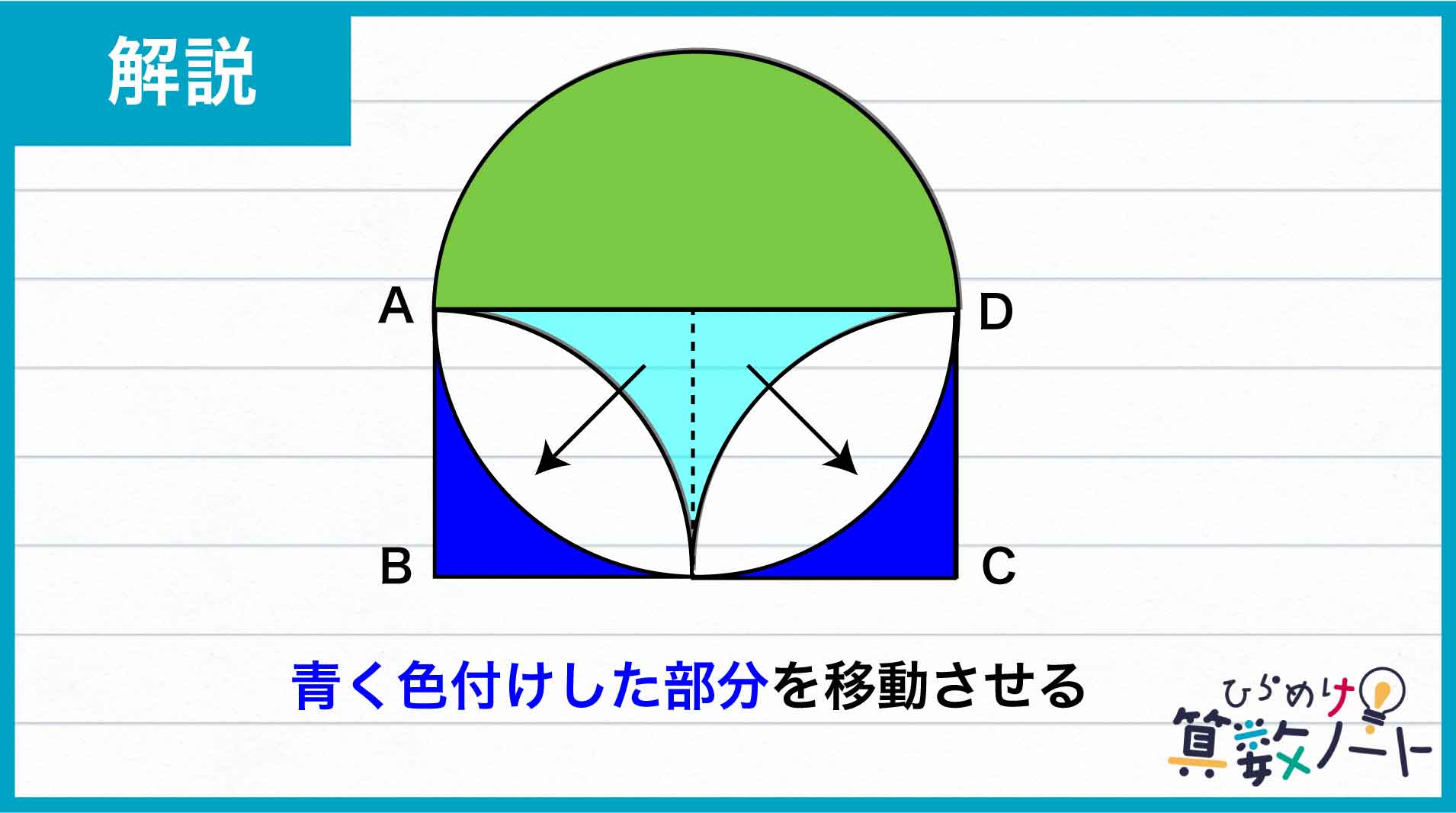
さらに、図形を分割してできた「半円」の部分を移動させます。

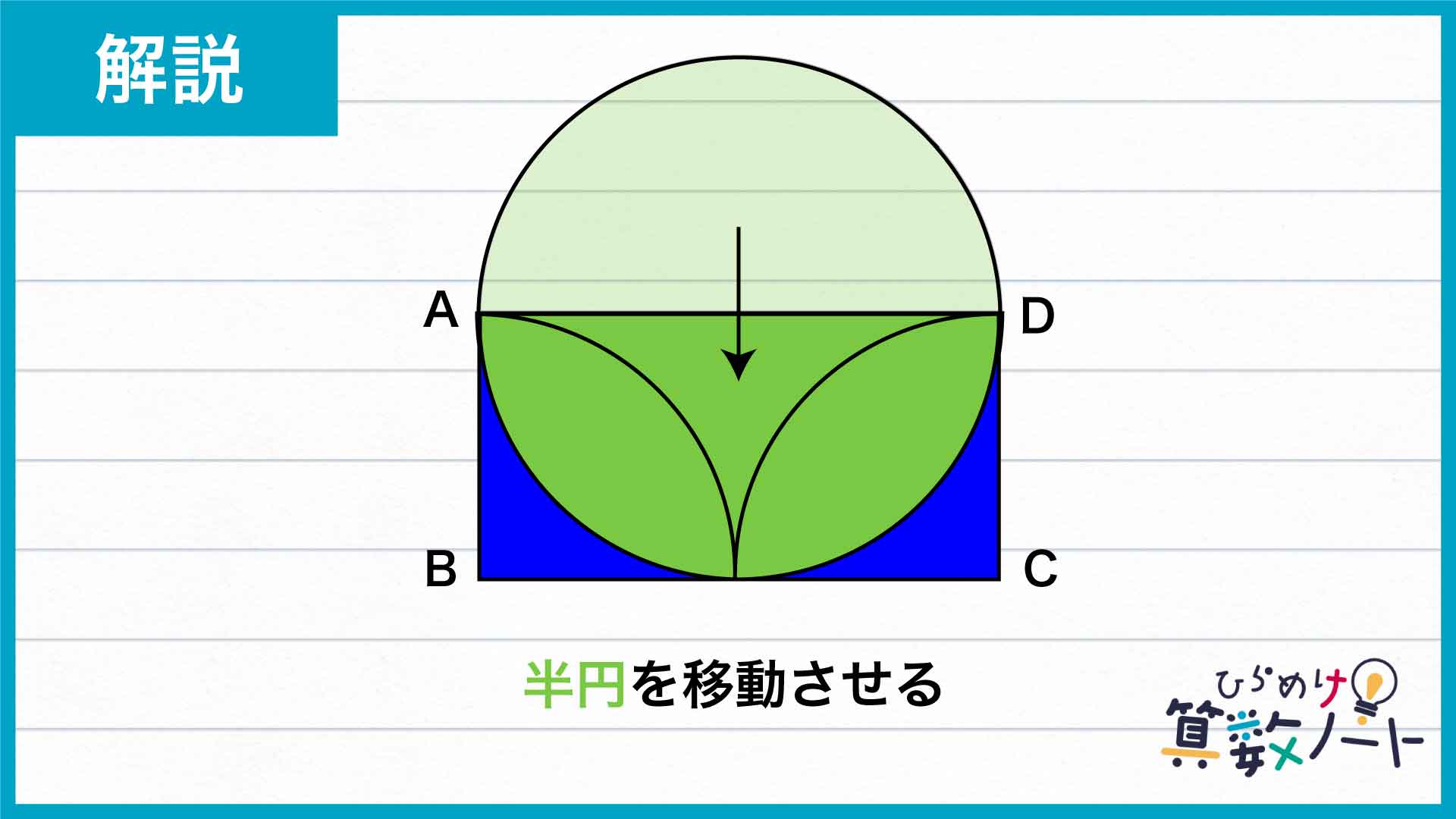
そうすると、注目した図形の面積は、下のような長方形の面積と等しくなります。

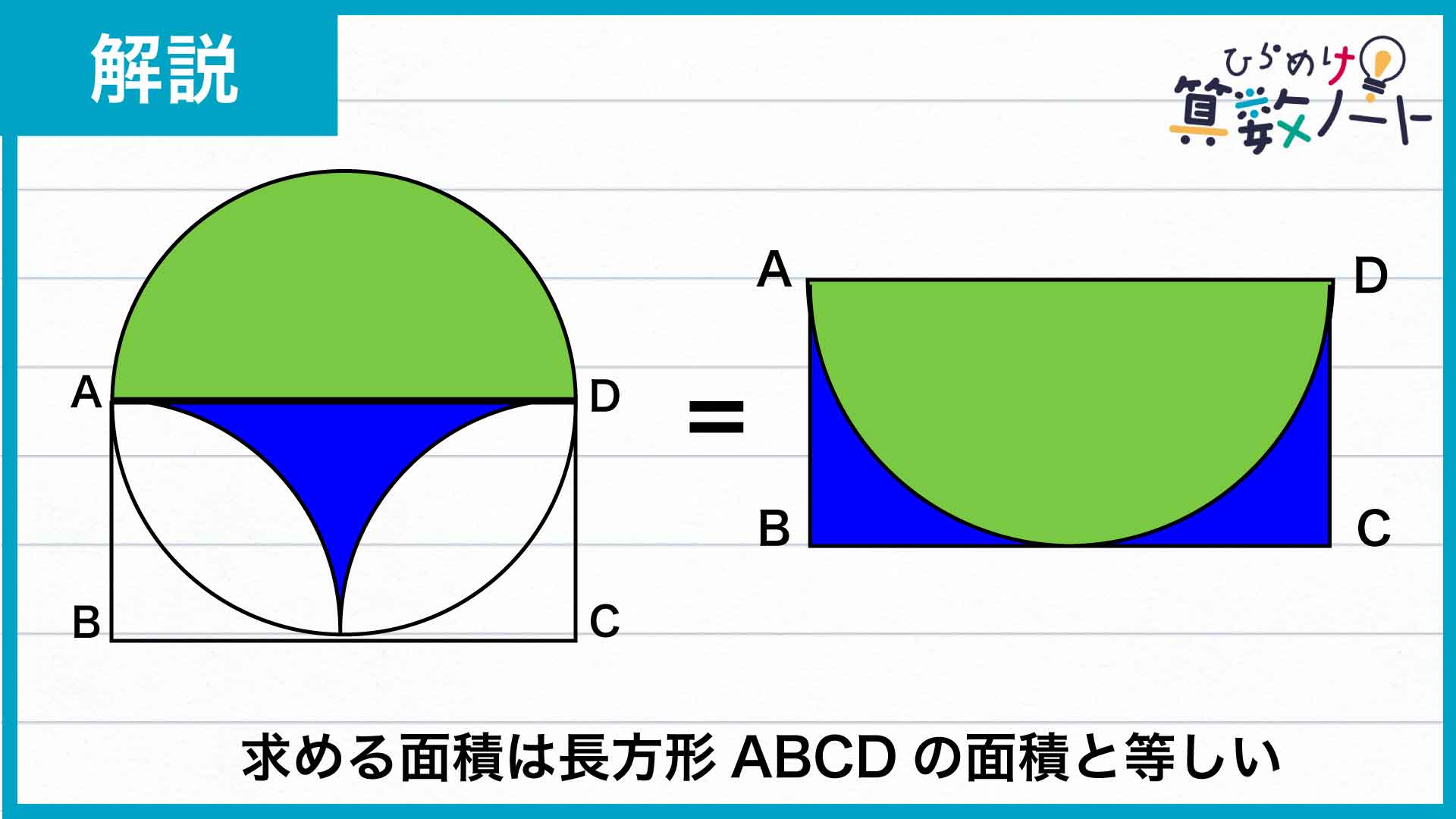
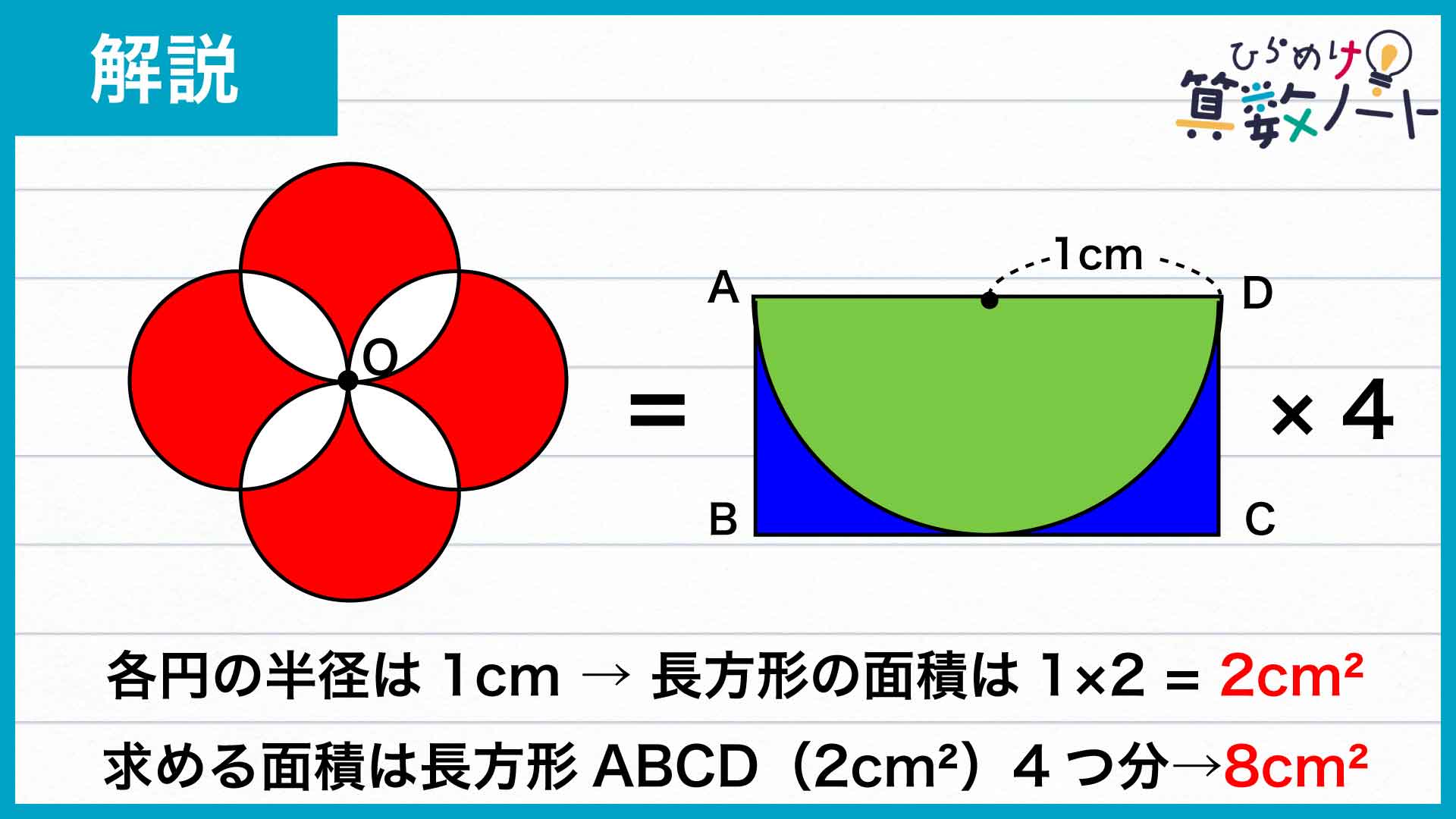
この長方形は、縦の長さが1cm（円の半径）、横の長さが2cm（円の直径）なので、その面積は1×2=2cm2となります。

問題の図形の面積は、長方形ABCDの面積の4つ分なので、その面積は2×4=8cm²となります。

答え：8cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】