解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
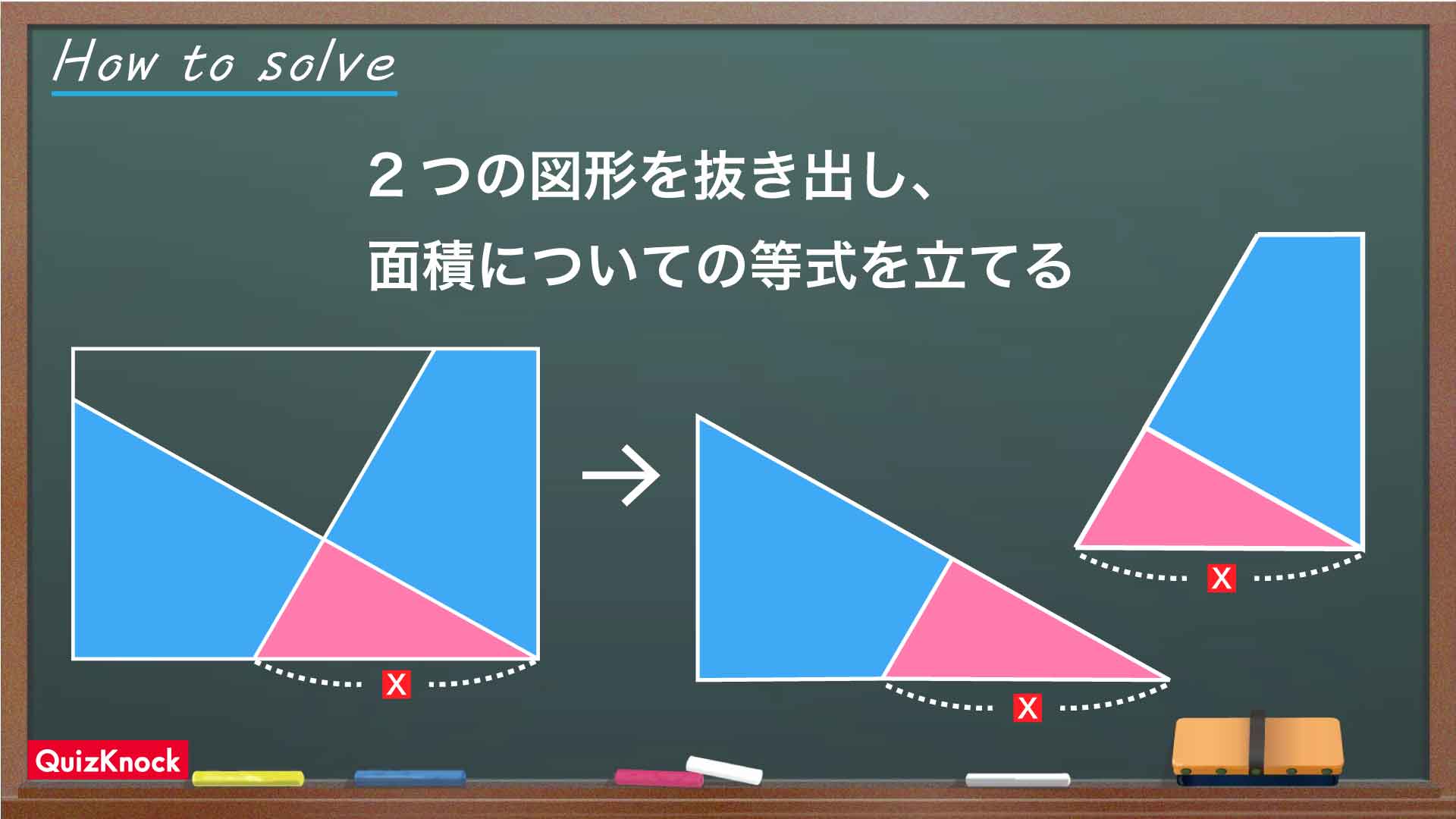
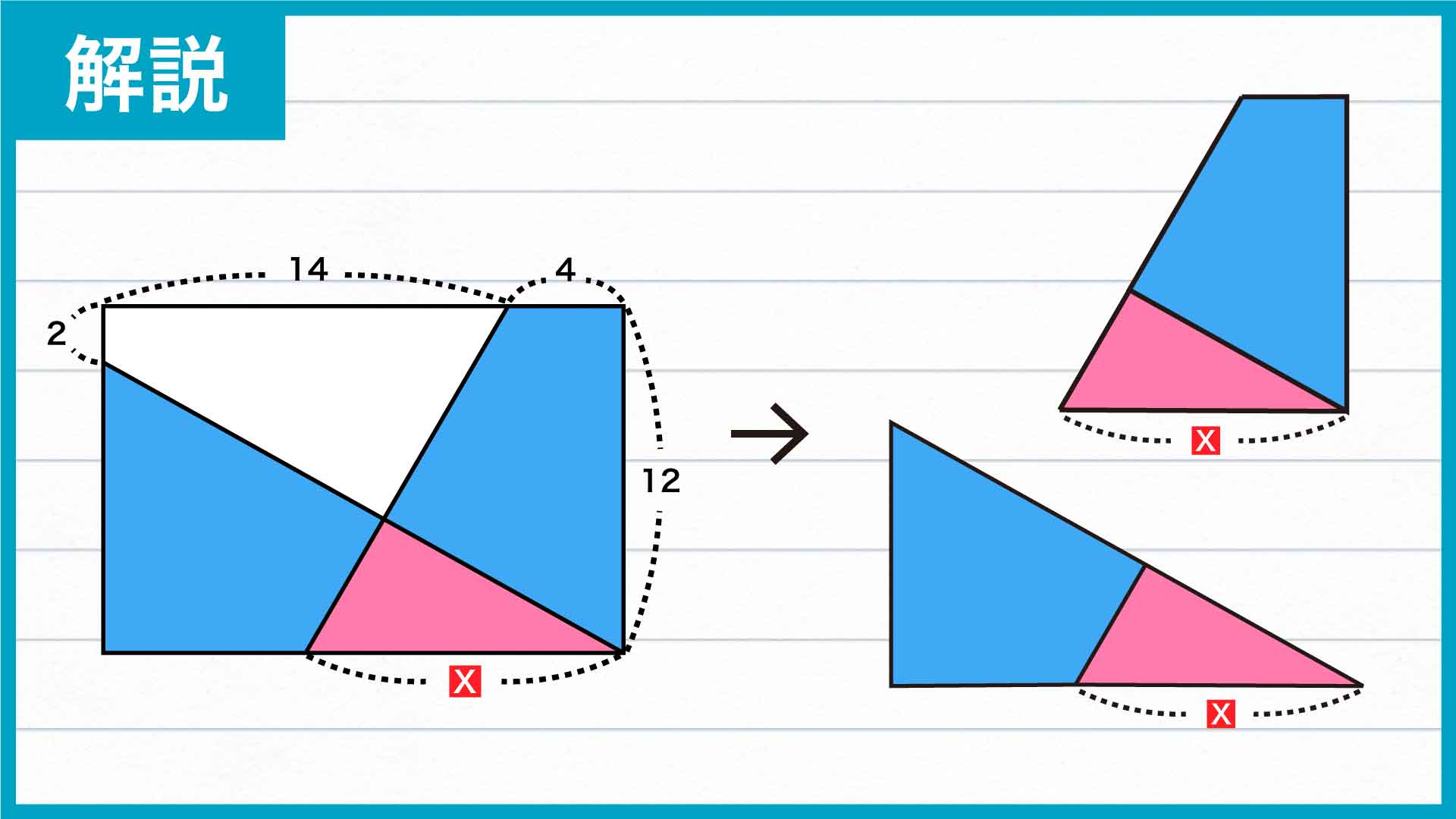
今回の解き方をまとめた図がこちらです。
今回のポイントは、「2つの青色の四角形に共通の三角形を組み合わせて、面積を求めやすい図形を作る」ことです。
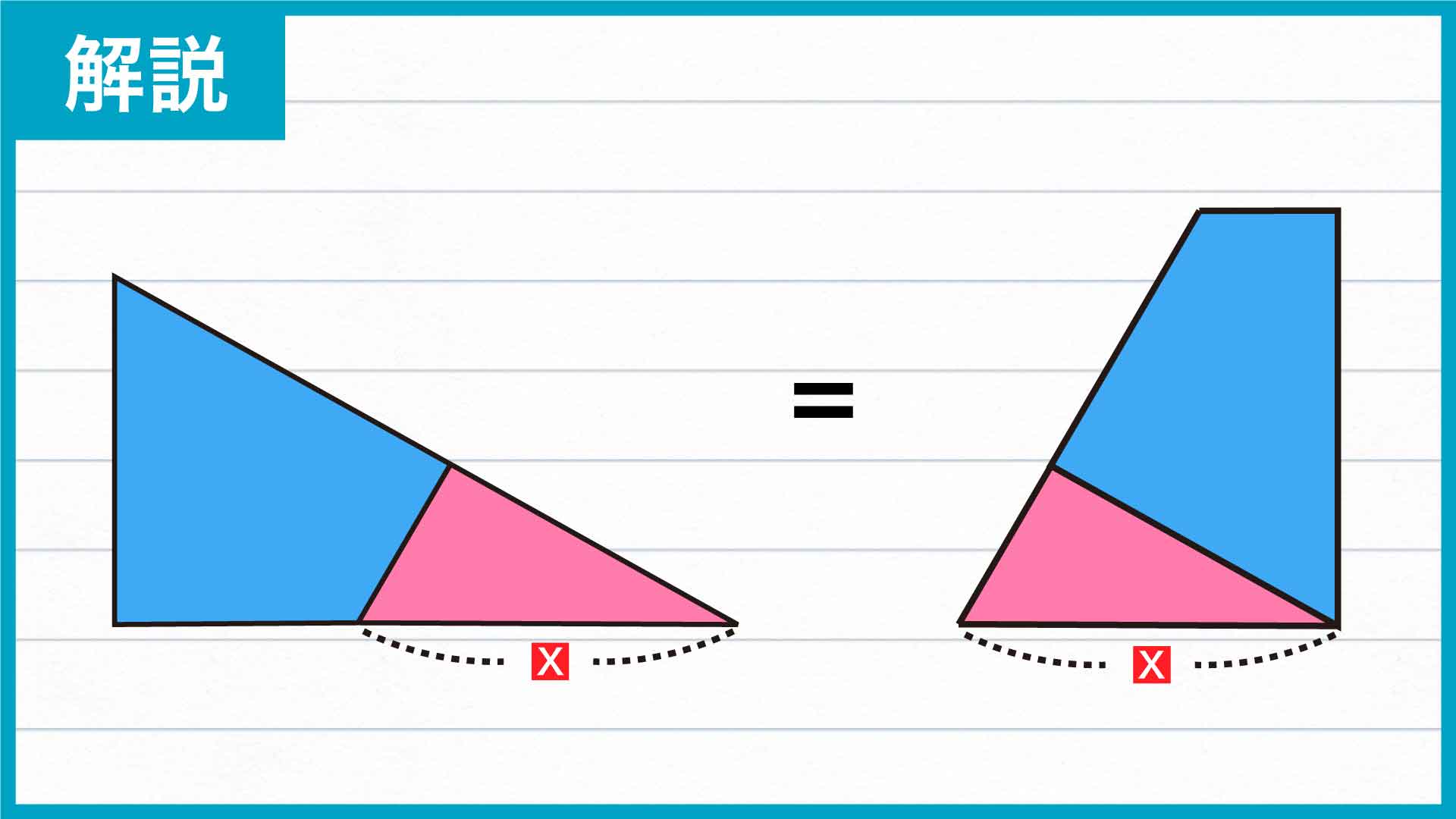
2つの青色の四角形の面積は等しいので、それぞれにピンク色の三角形を足してできる三角形と台形の面積も等しくなります。それらの図形の面積を経由することで、Xを求めることができるのです。
このポイントをもとに、問題を攻略していきましょう!
面積が等しい図形を作る
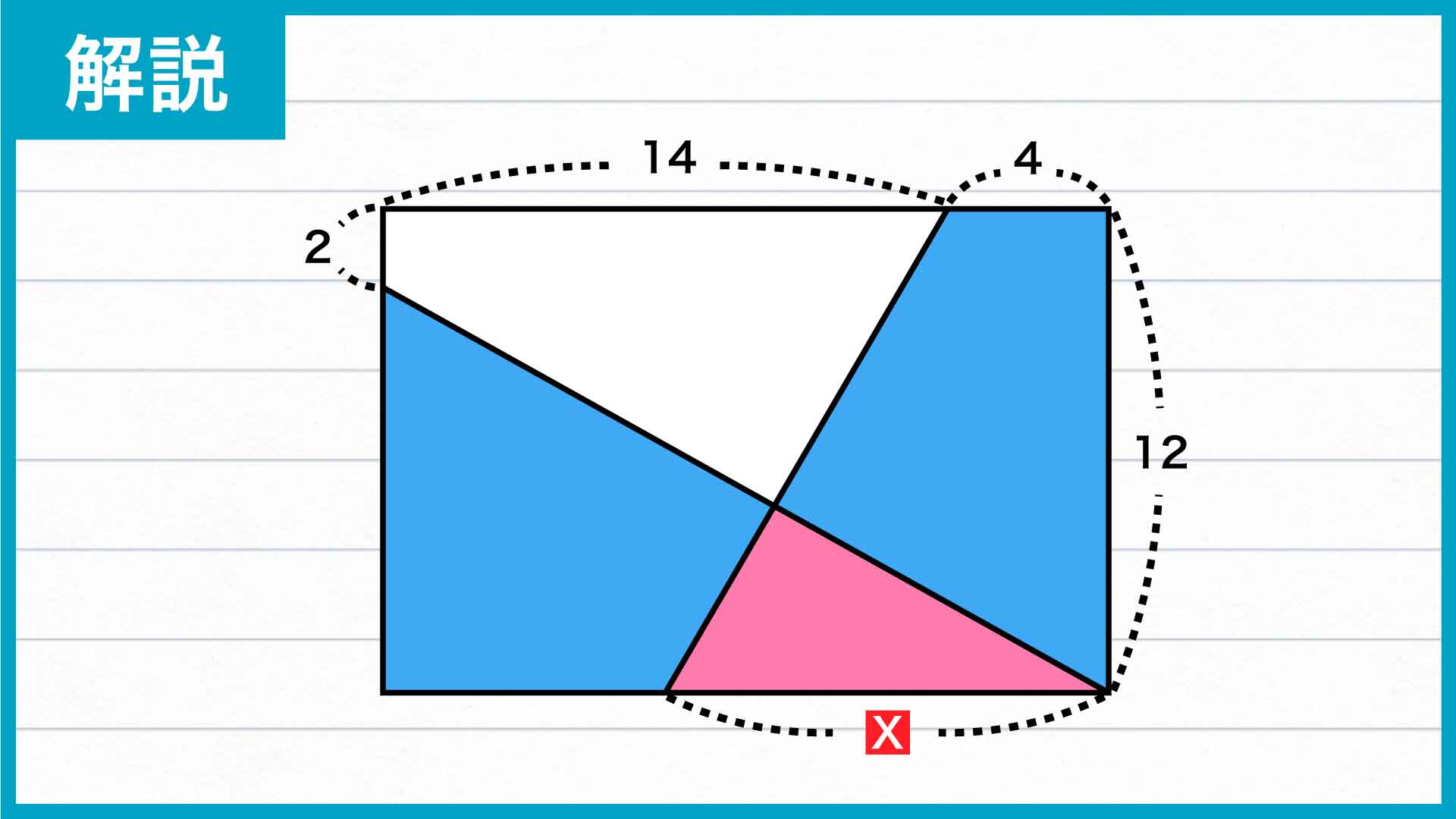
それぞれの青色の四角形に、下の図のようにピンク色の三角形を組み合わせます。
すると、長方形の中で台形と三角形を作ることができます。
ここで、2つの青色の四角形の面積は等しいので、それぞれに共通のピンク色の三角形を合わせて作った台形と三角形も面積が等しいことがわかります。
三角形と台形の面積を求める
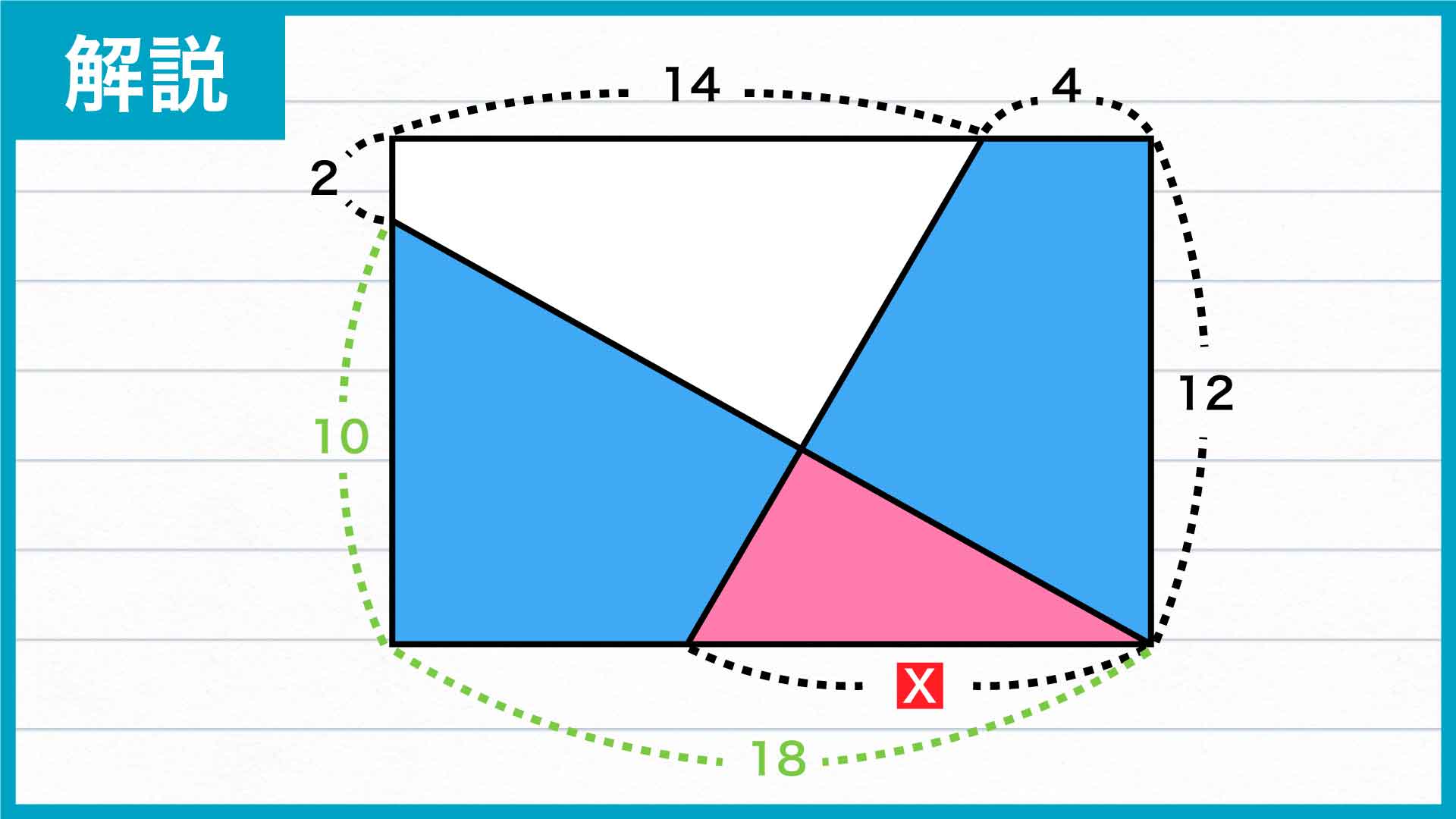
青色の四角形とピンク色の三角形を組み合わせて作った三角形の面積は、以下の図のように、底辺の長さが18、高さが10となっています。
したがって、三角形の面積は、18×10÷2=90と求めることができます。
また、青色の四角形とピンク色の三角形を組み合わせて作った三角形と台形の面積は等しいので、台形の面積も90であることがわかります。
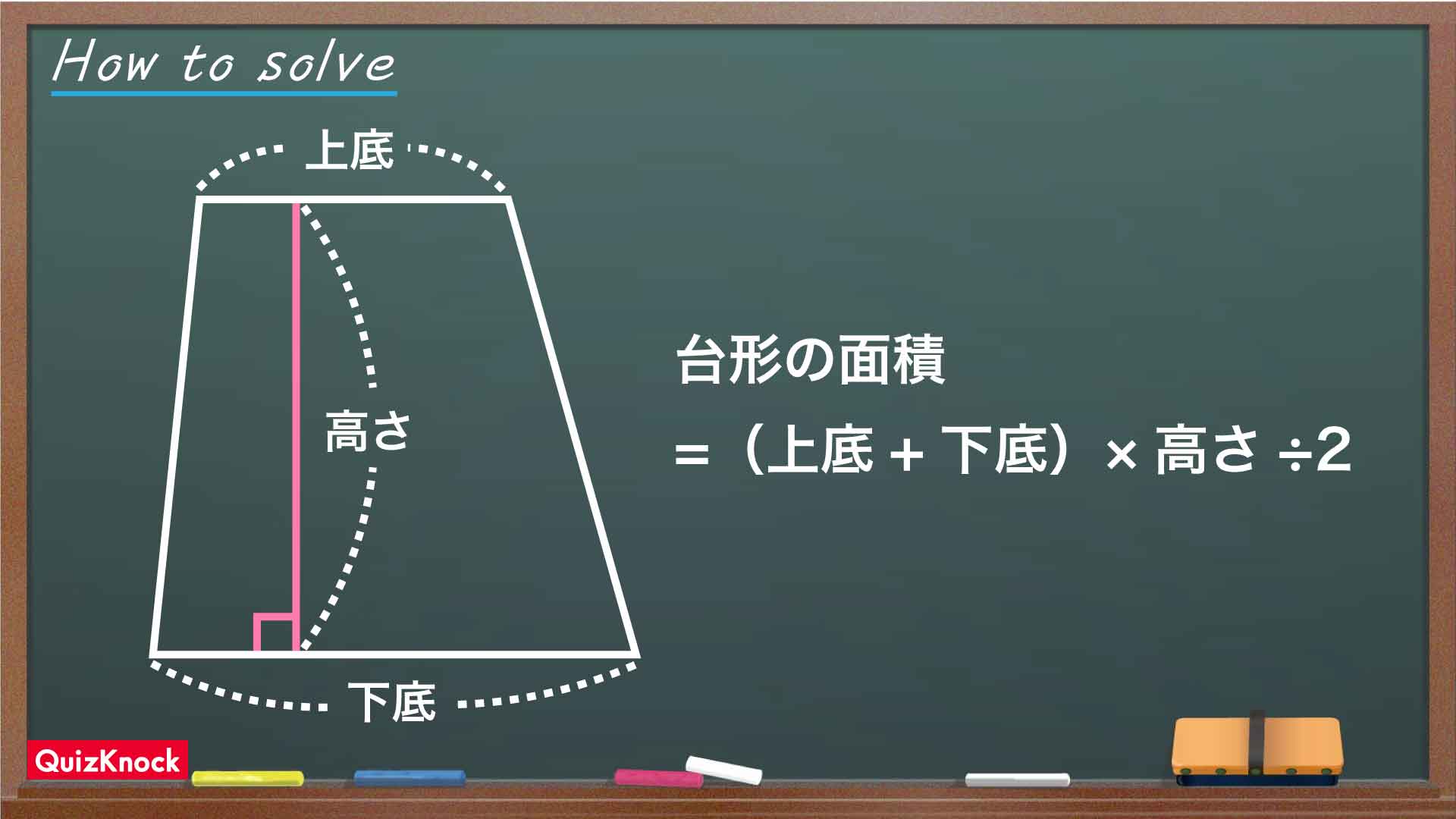
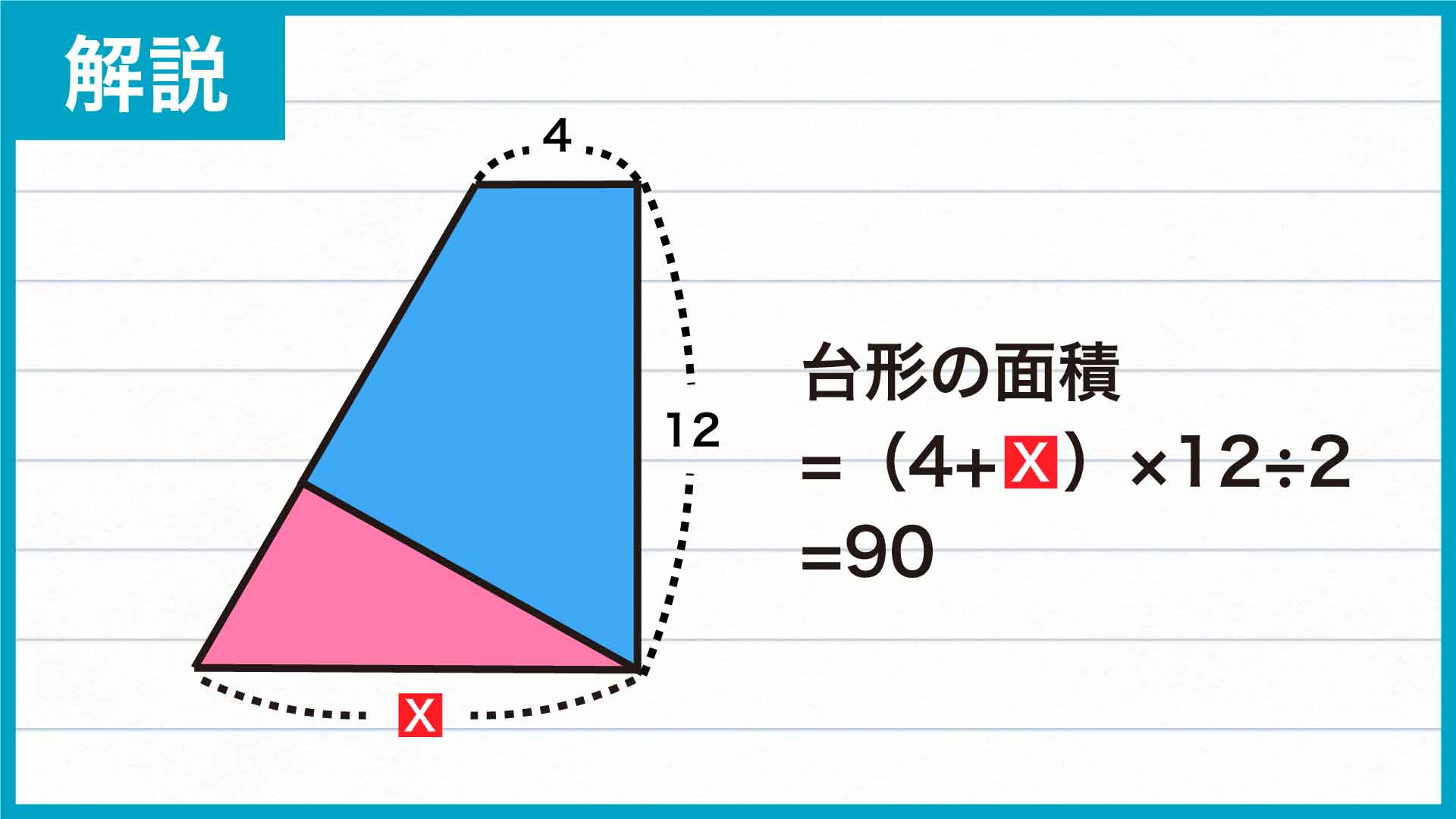
台形の面積の公式は?
台形の面積は、以下の公式を使って求めることができます。
青色の四角形とピンク色の三角形を組み合わせた台形において、上底の長さは4、下底の長さはX、高さは12となっています。
したがって、これを公式に適用すると、(4+X)×12÷2=90という式を立てることができます。
この式を以下のように式変形していくと、Xには11が入ることがわかります。
したがって、Xの長さは11となります。
答え:11
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)







.jpg)







