小学6年生で解ける「図形の面積」の問題。あなたは解ける？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の重要なポイントはこちらです。

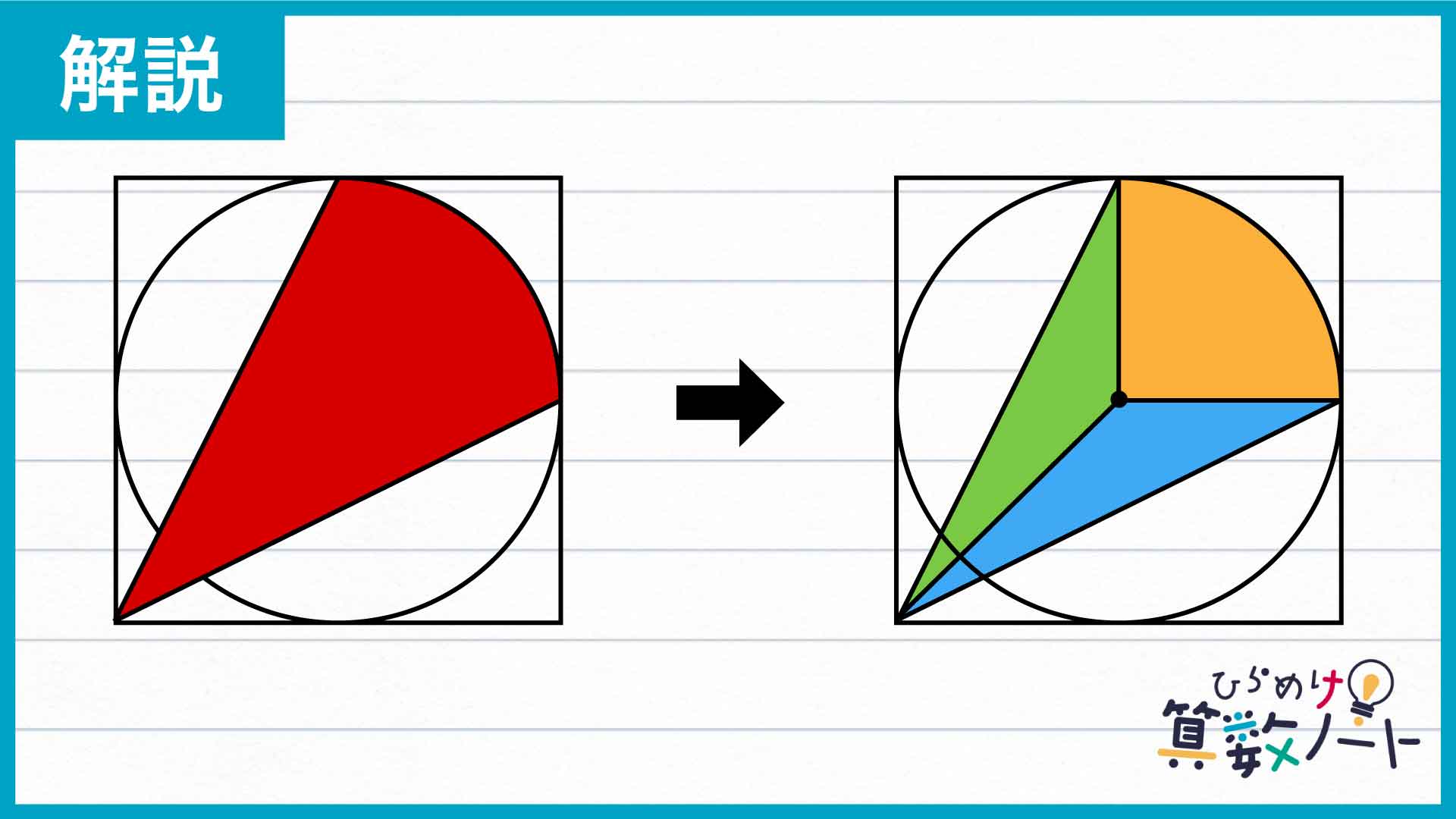
ポイントは、問題の赤い図形に補助線を引いて扇形1つと三角形2つという、面積を求めやすい図形に分割することです。

赤い図形を分割する

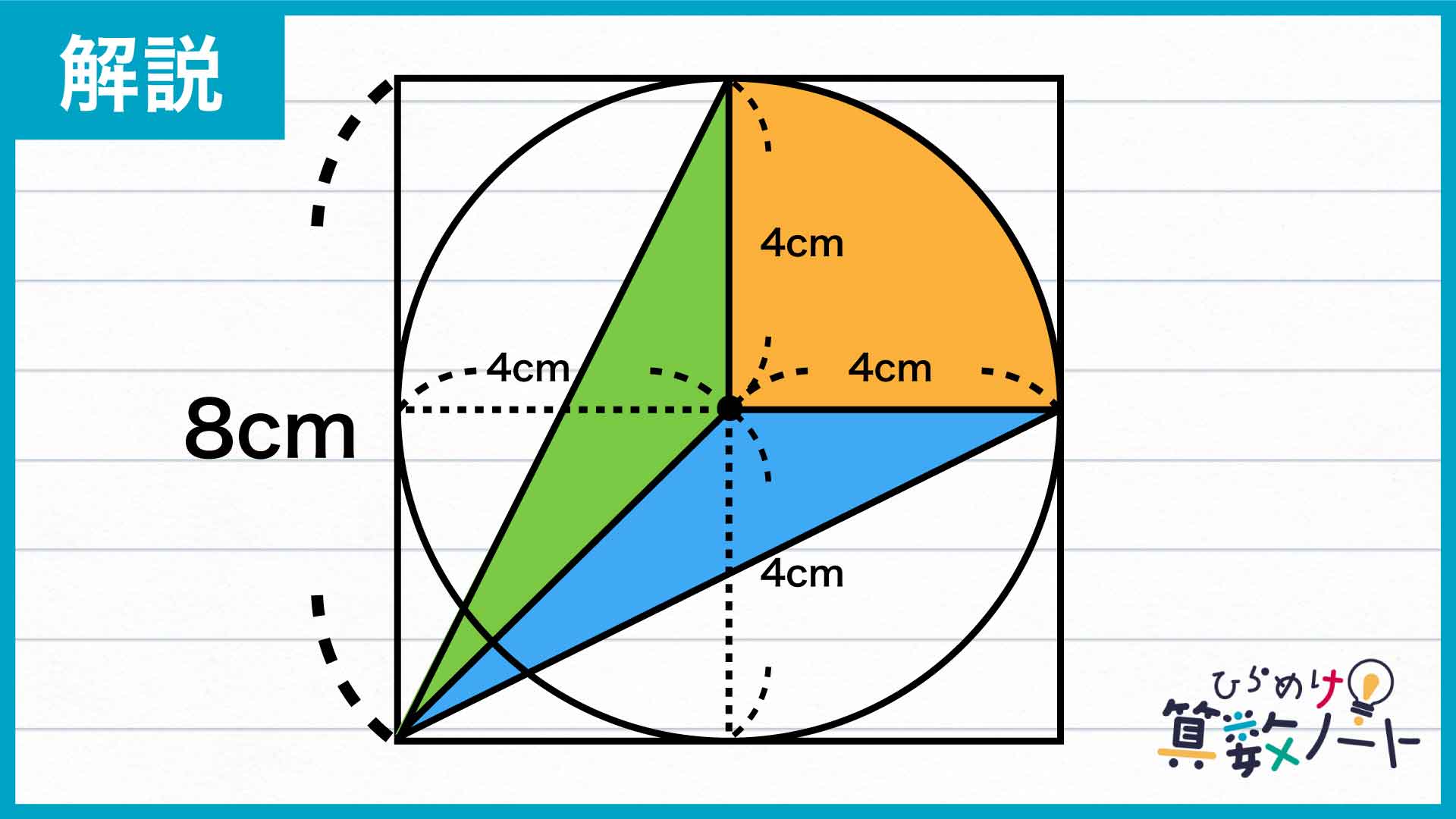
まずは下の図のように、円の中心から正方形の左下の頂点、および2つの正方形と円の接点にそれぞれ線を引きます。すると、問題の赤い図形は扇形1つと三角形2つに分割することができます。

分割してできた図形の面積をそれぞれ求める

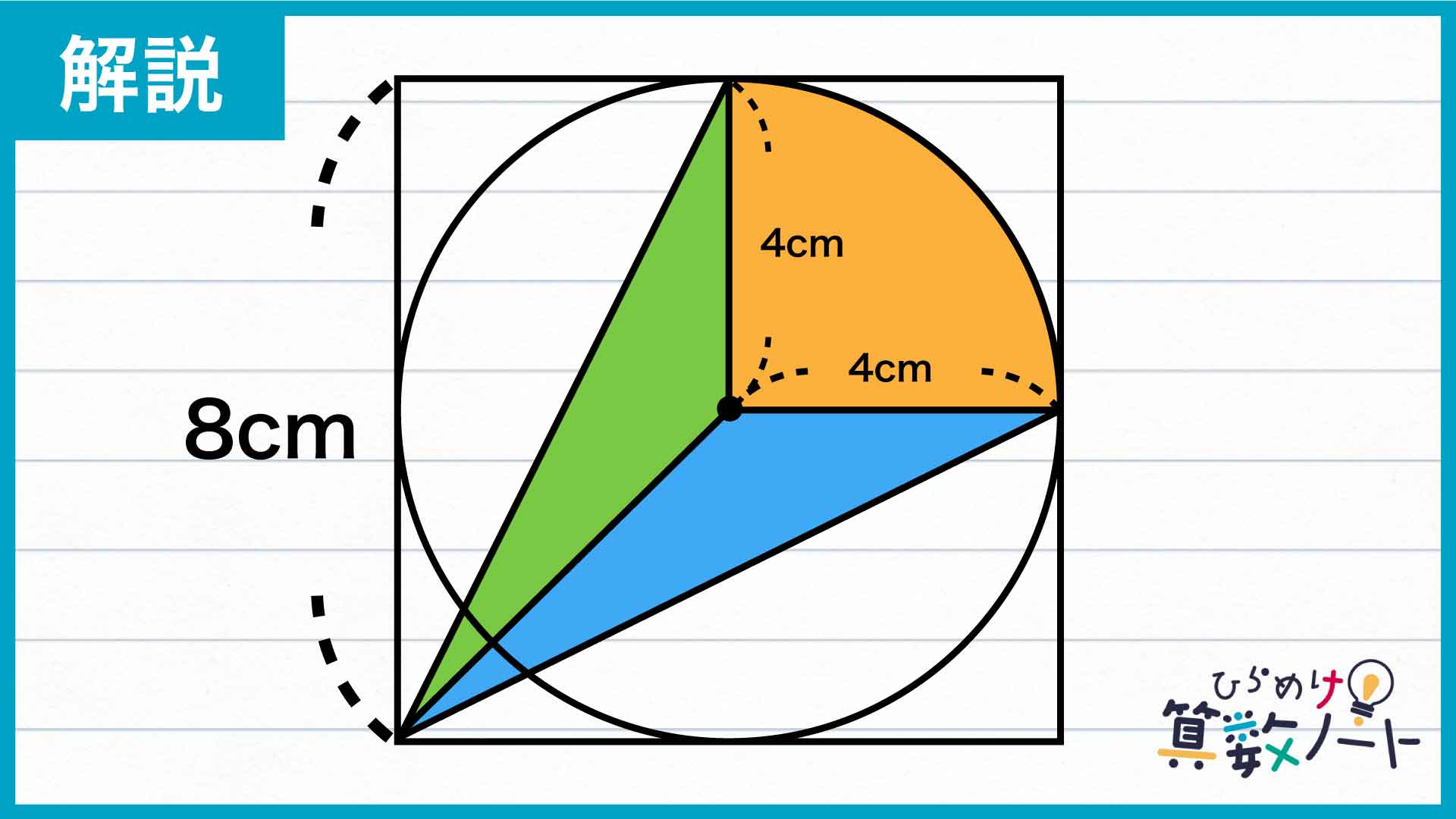
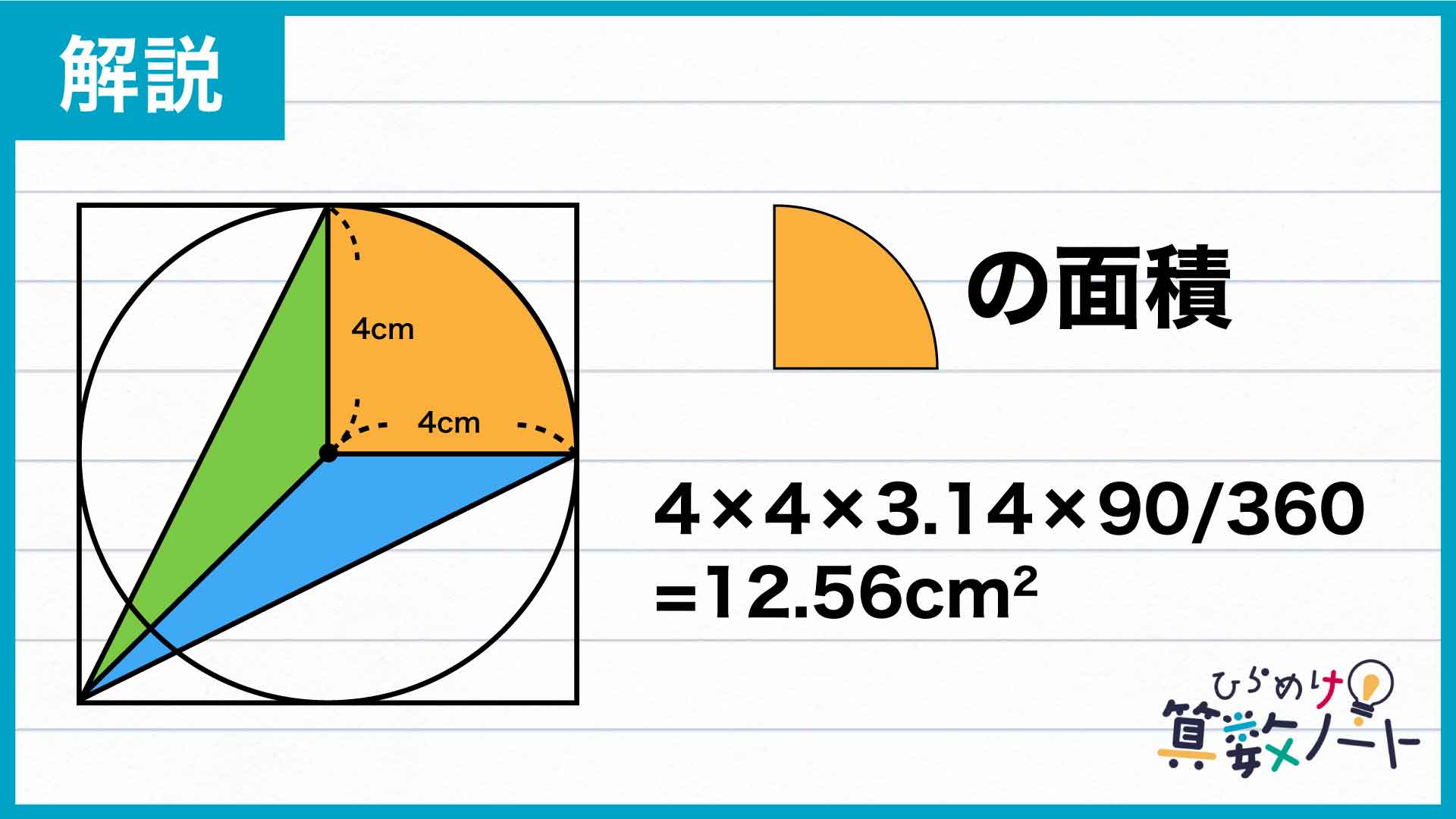
まずは黄色い扇形の面積を求めます。黄色い扇形は正方形内の円の一部なので、半径が4cm、中心角が90度の扇形だとわかります。

したがって、黄色い扇形の面積は4×4×3.14×(90/360)=12.56cm²と求めることができます。

次に、2つの三角形の面積を求めます。そこで、新たに2つの補助線を引きます。

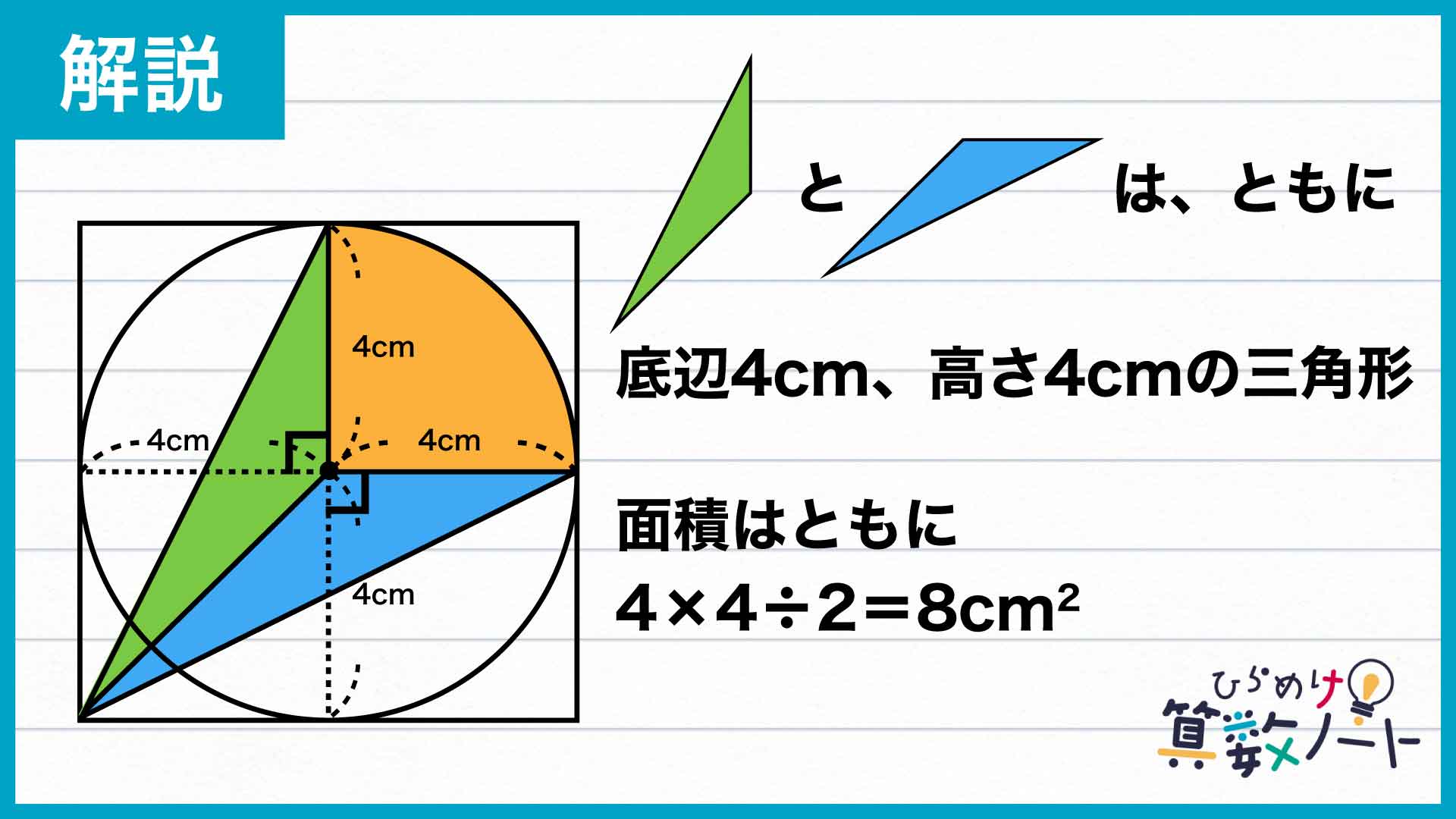
下の図の点線のように、円の中心から正方形と円の接点に向かって線を引きます。すると、緑の三角形における底辺を黄色い扇形の半径の部分とすると、高さは横に引いた点線ということになります。同様に、青の三角形の底辺を黄色い扇形の半径の部分とすると、高さは縦に引いた点線ということになります。

したがって、緑と青の三角形はどちらも底辺が4cm、高さが4cmの三角形なので、2つの三角形の面積はそれぞれ4×4÷2=8cm²となります。

問題の赤い面積は黄色い扇形と青と緑の三角形を足し合わせたものなので、赤い図形の面積は12.56+8+8=28.56cm²となります。

答え：28.56cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】