解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
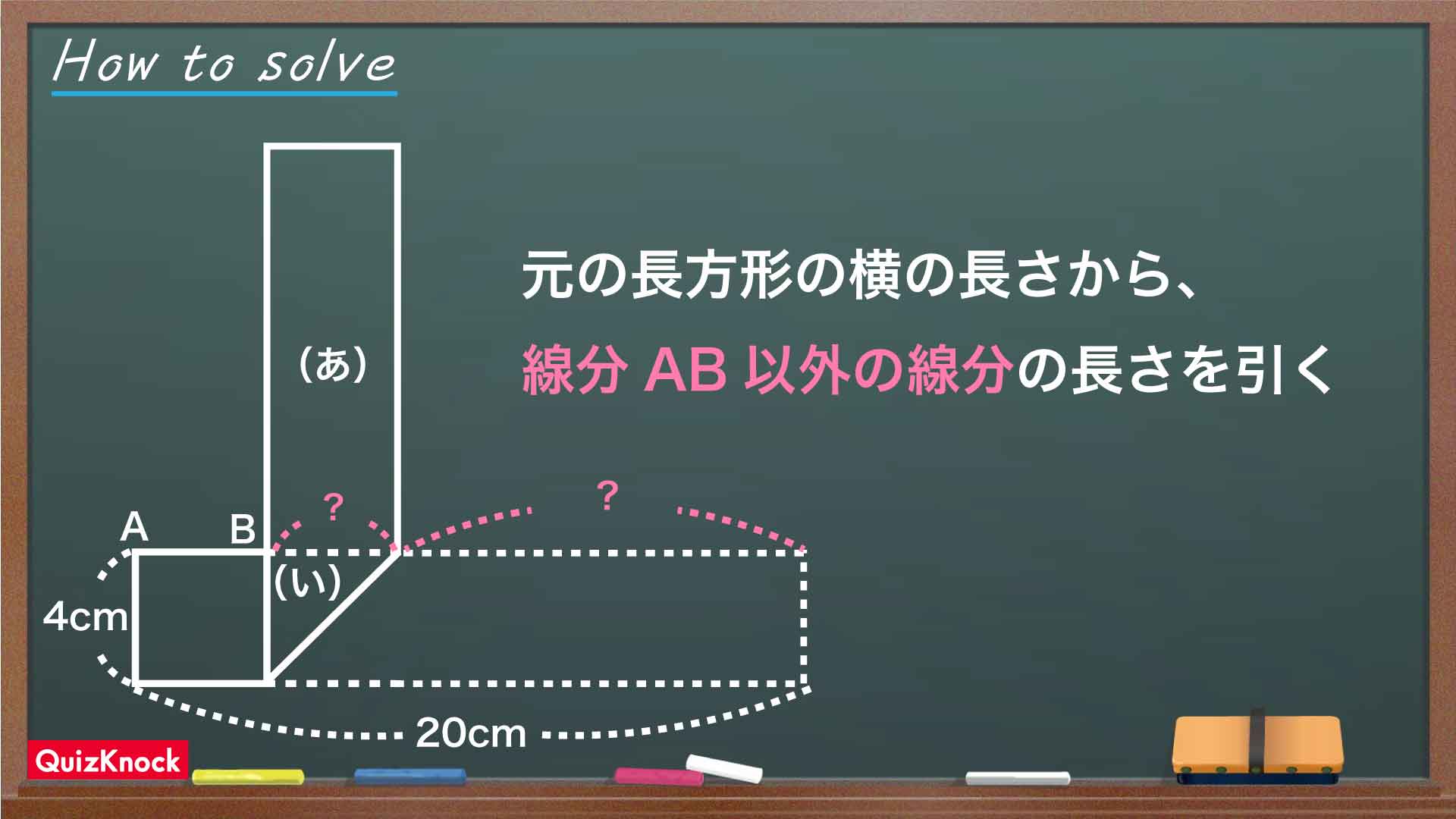
今回の解き方をまとめた図がこちらです。
今回のポイントは、「面積から逆算して必要な線の長さを求める」ことです。
このポイントをもとに、問題を攻略していきましょう!
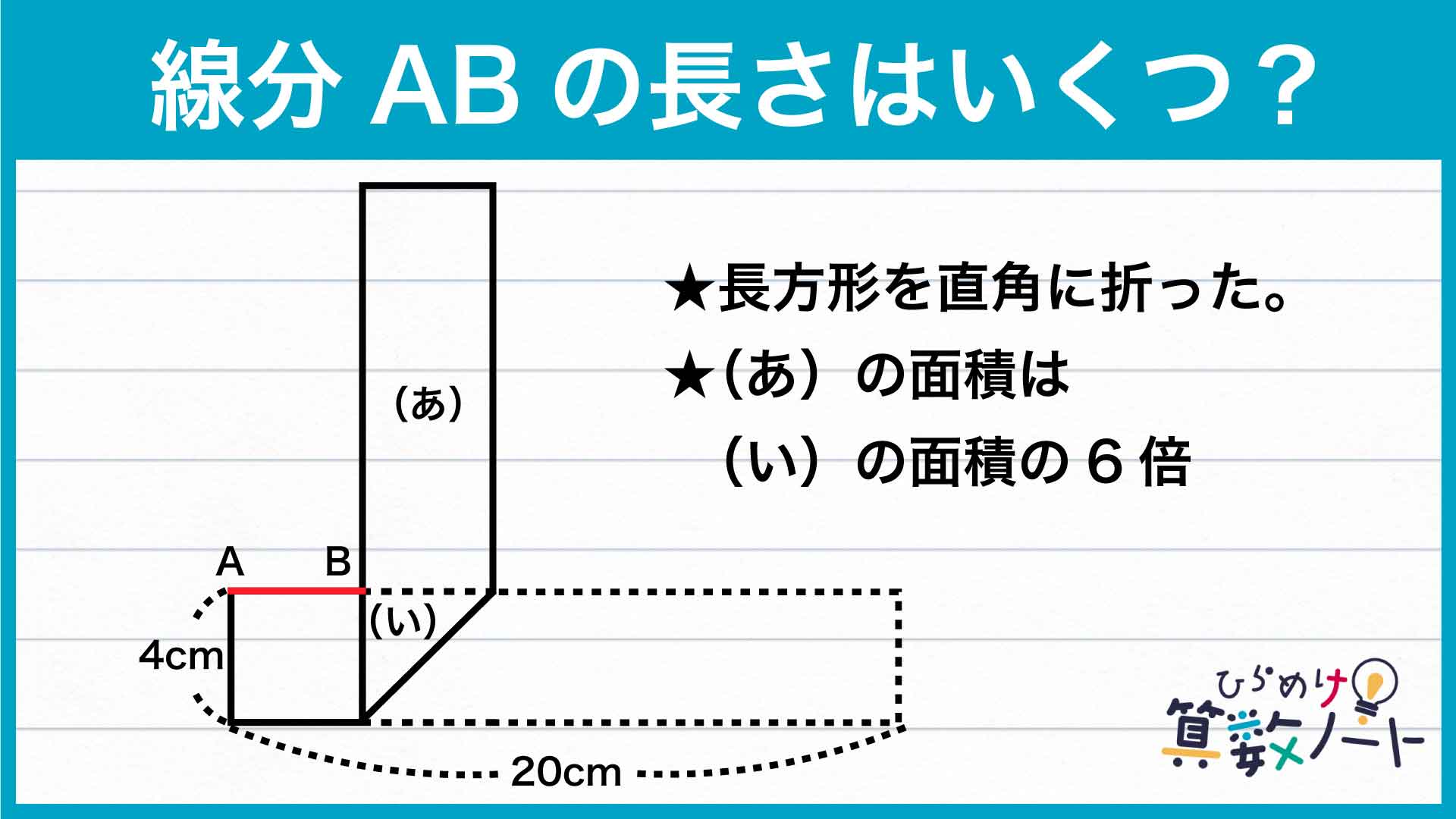
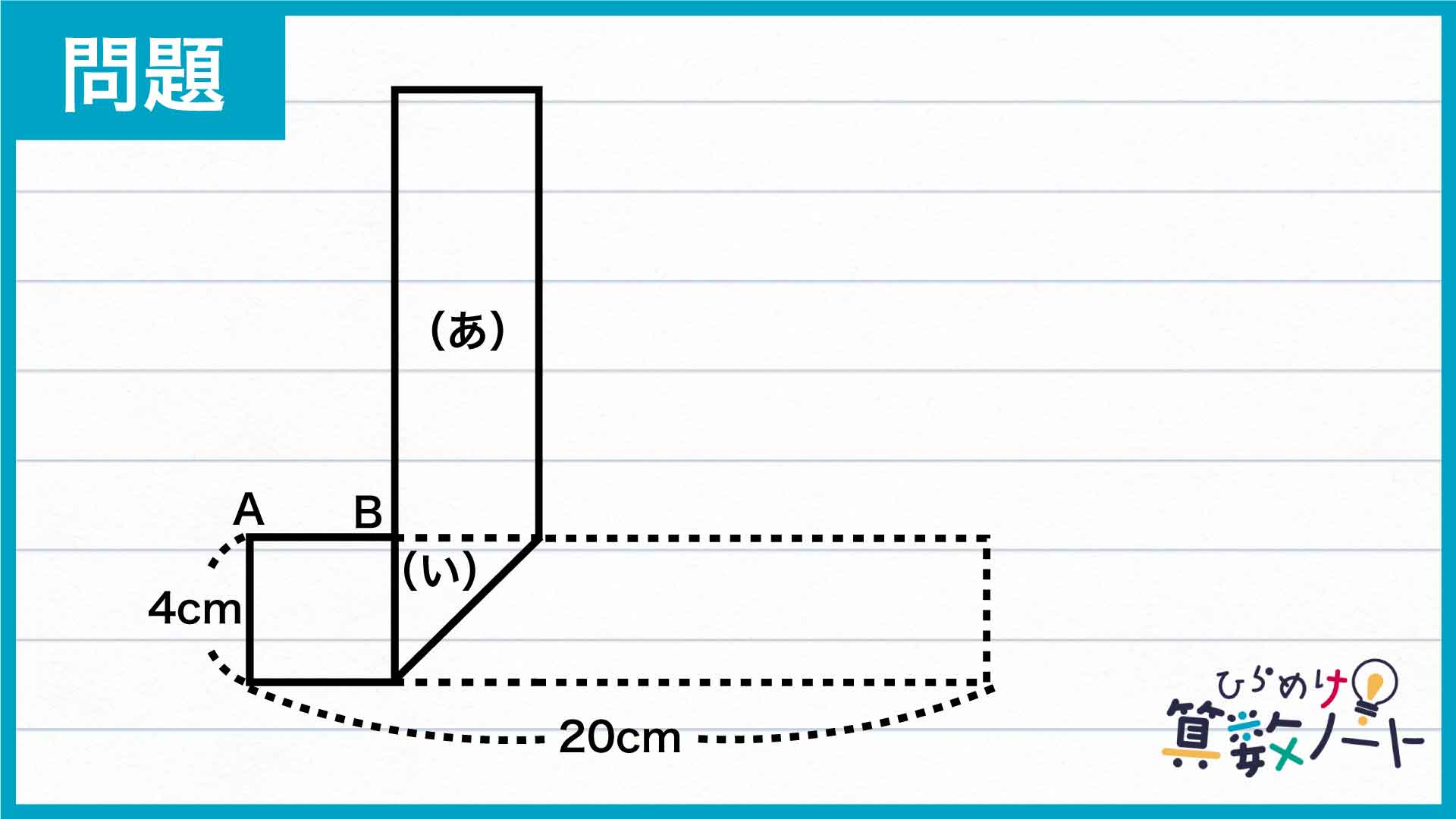
三角形 (い)と長方形(あ)の面積を求める
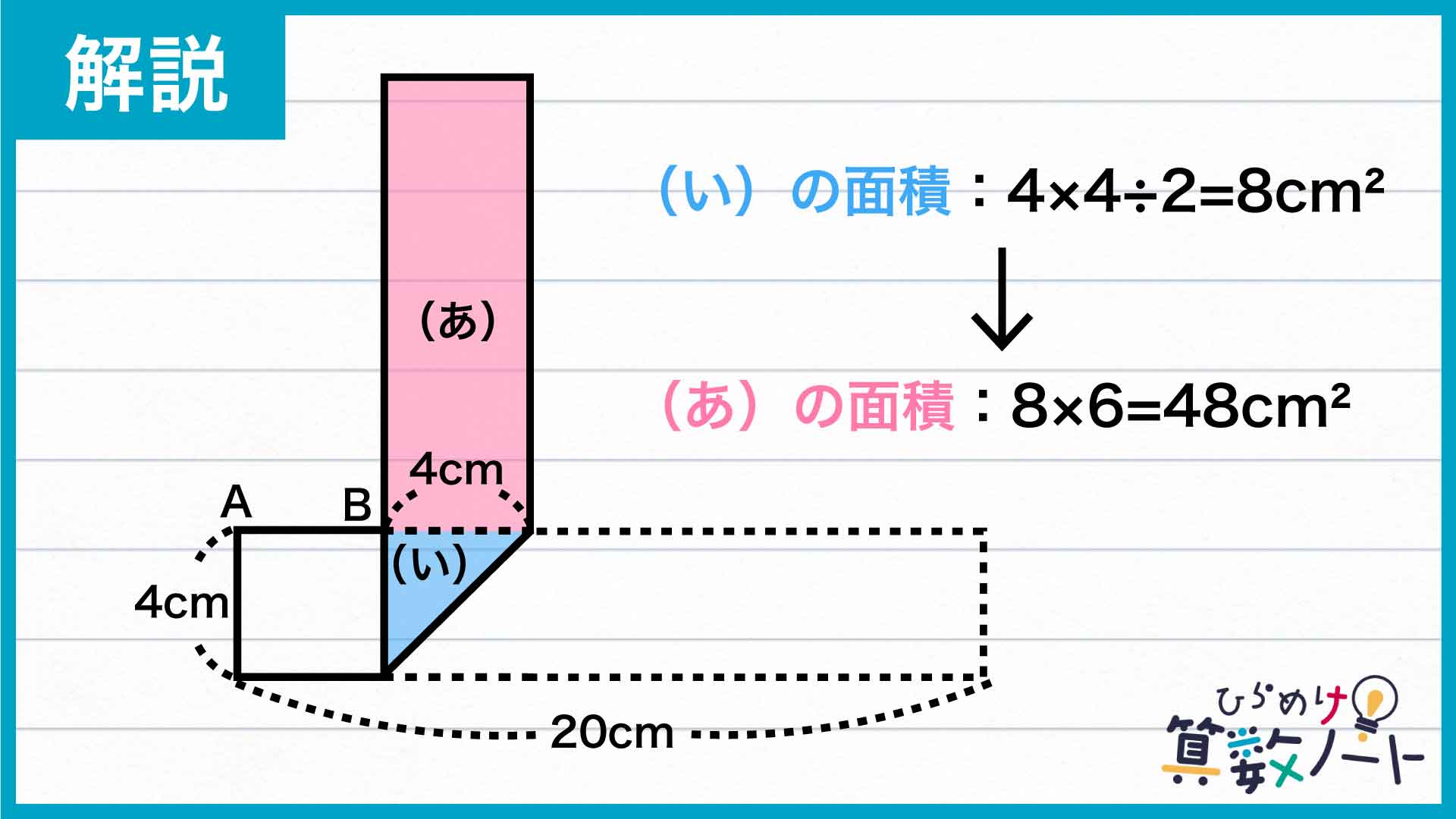
三角形(い)は長方形の中の図形なので、高さは長方形と同じ4cmです。また、図は長方形を直角に折ったものなので、三角形(い)の底辺の長さも4cmであることがわかります。
したがって、三角形(い)の面積は4×4÷2=8cm2となります。
また、長方形(あ)の面積は三角形(い)の面積の6倍なので、8×6=48cm2とわかります。
長方形(あ)の長辺の長さを求める
長方形(あ)の短辺の長さは、折り曲げる前の長方形と同じ4cmです。したがって、長辺の長さは48÷4=12cmと求めることができます。
ここで、下の図に示した長方形を長方形(う)とします。
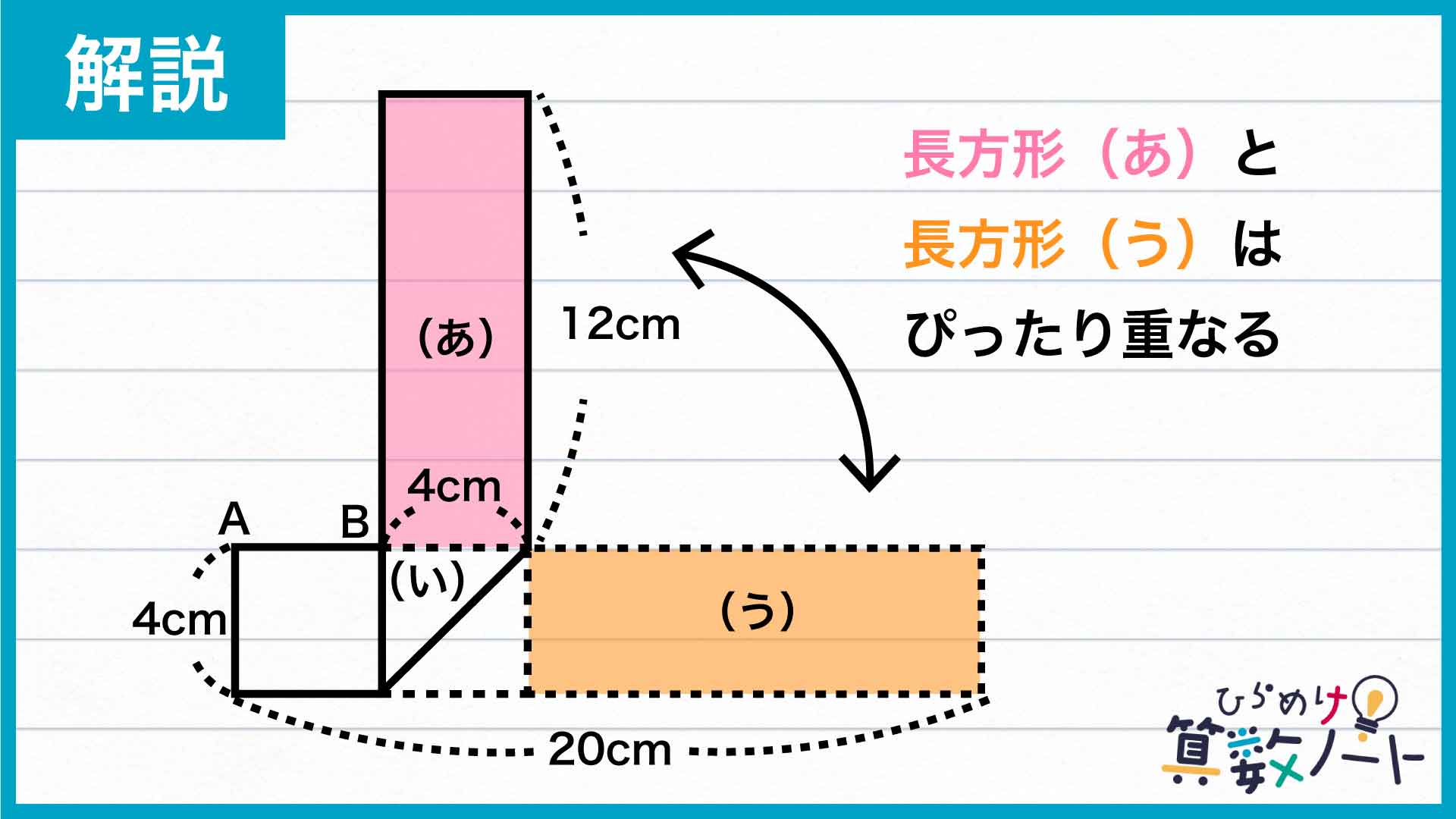
長方形(う)は折り曲げる前の長方形(あ)の部分にあたるので、長方形(あ)と長方形(う)はぴったり重ねることができます。
したがって、先ほど求めた長方形(あ)の長辺の長さは、長方形(う)の長辺の長さと同じであることがわかります。
以上より、わかっている長さの情報をまとめると下の図のようになります。
したがって、求める線分ABの長さは、20-(12+4)=4cmとなります。
答え:4cm
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)










.jpg)







