解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
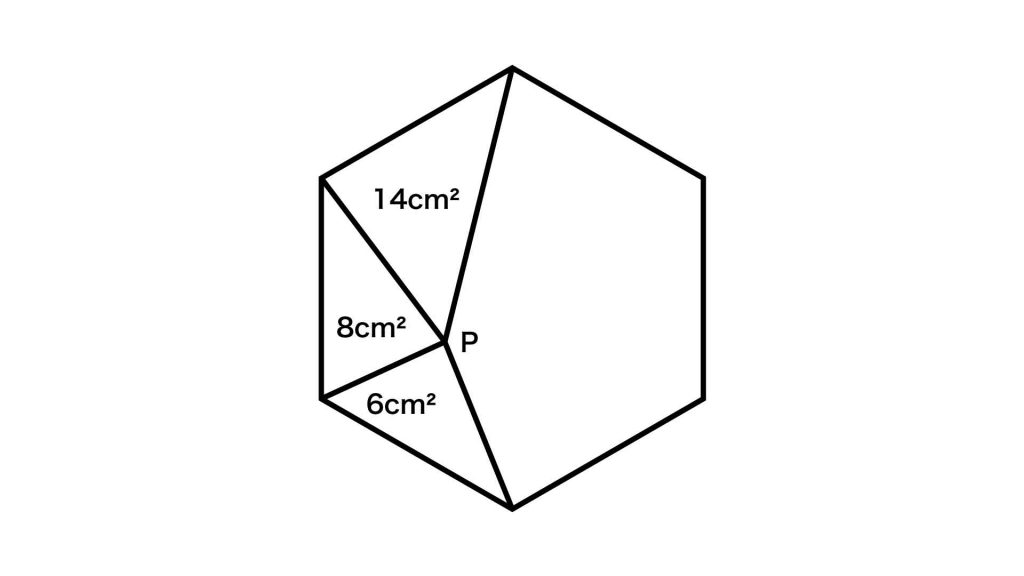
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回の解き方をまとめた図がこちらです。
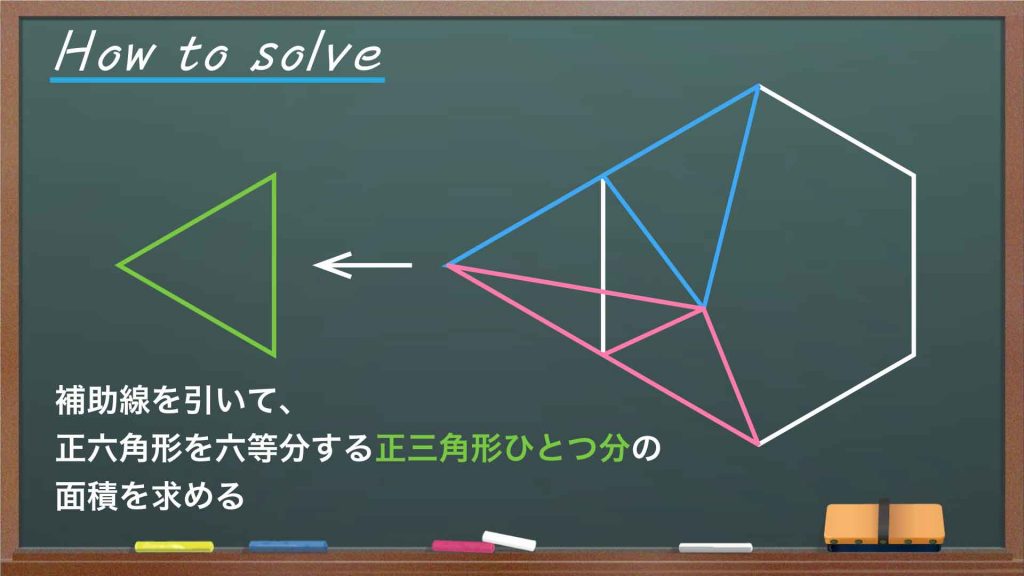
ポイントは、正六角形を六等分する「正三角形ひとつの面積」を求めることです。
この流れに沿って問題を攻略していきましょう!
正六角形の2辺の延長線を引く
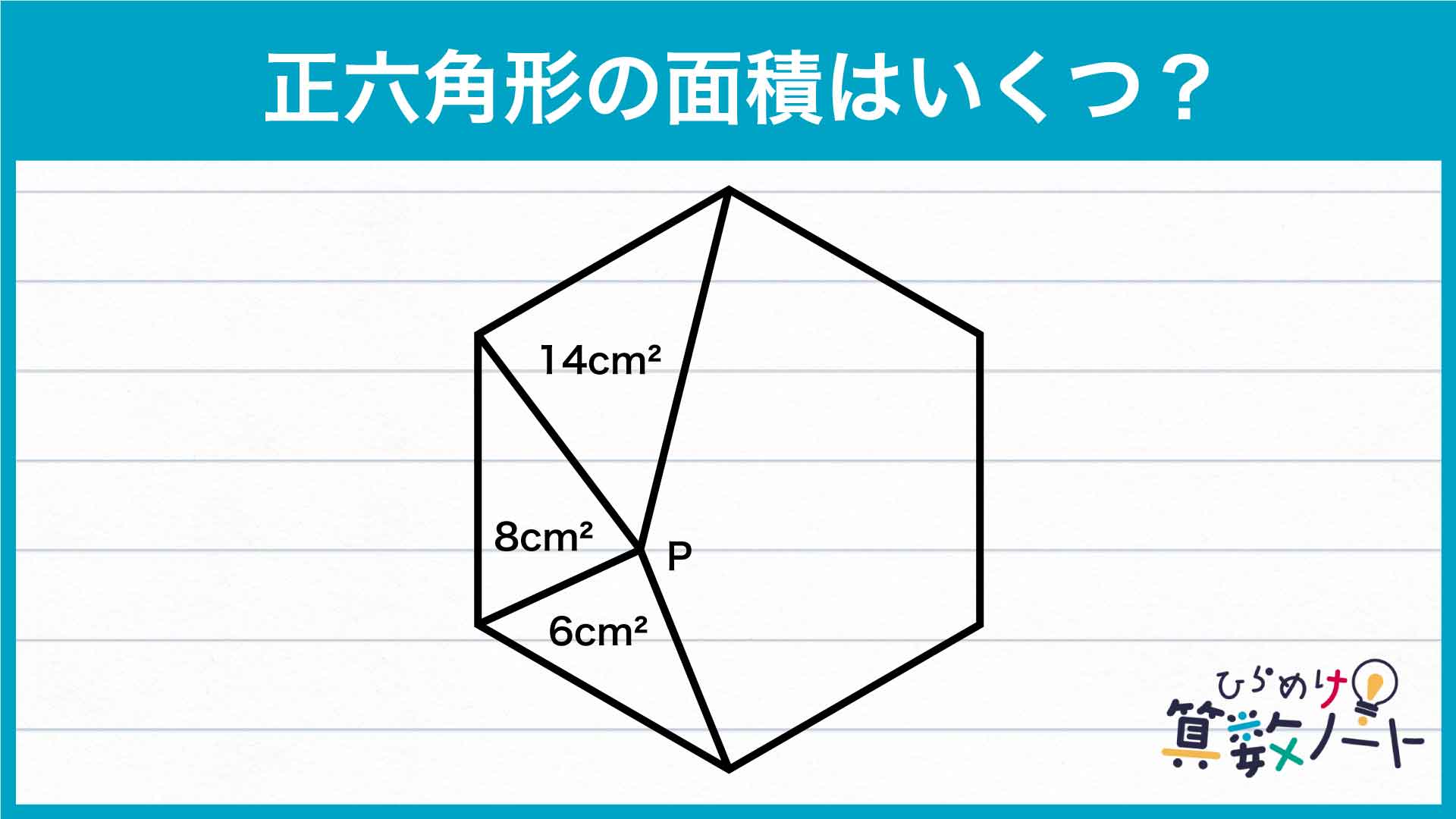
下の図のように、各点をA,B,C,Dとします。
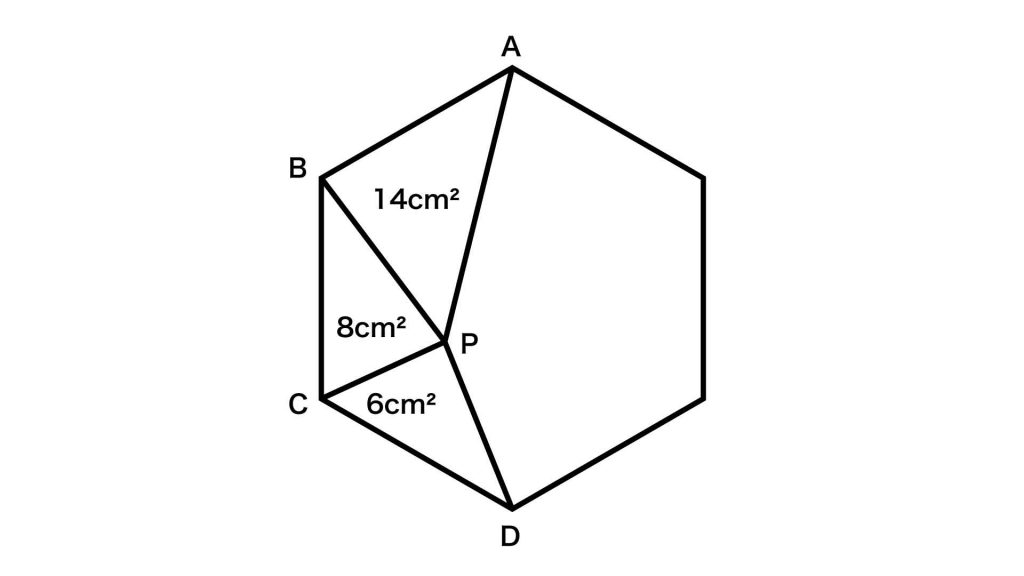
辺ABをB側に、辺DCをC側に延長し、正六角形の外側に三角形をつくります。2本の延長線が交差した点をEとします。
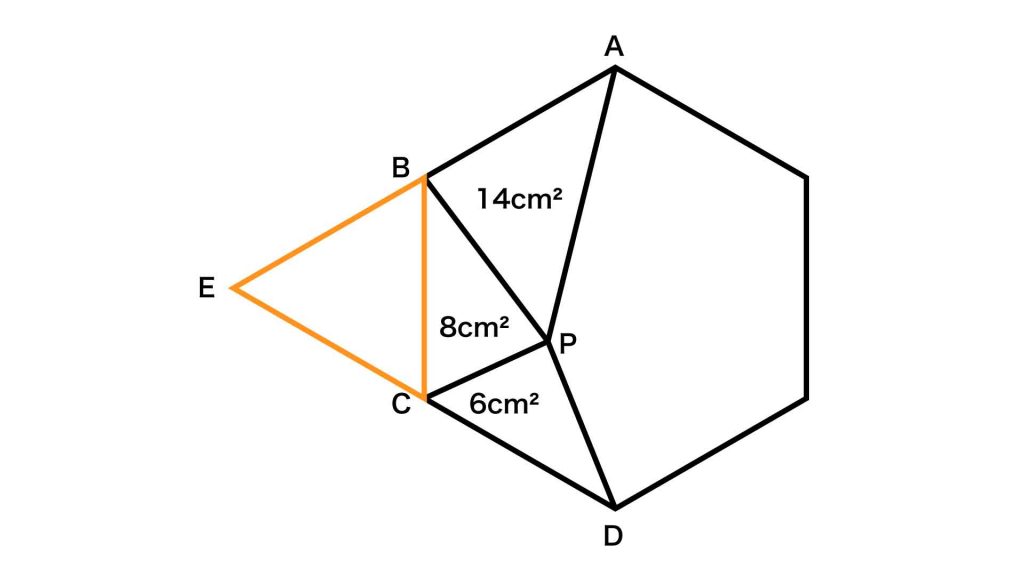
正六角形の内角ひとつの大きさは120度なので、角BCE=角CBE=180-120=60度です。すると、三角形BCEはすべての角の大きさが60度であるため、正三角形であることがわかります。
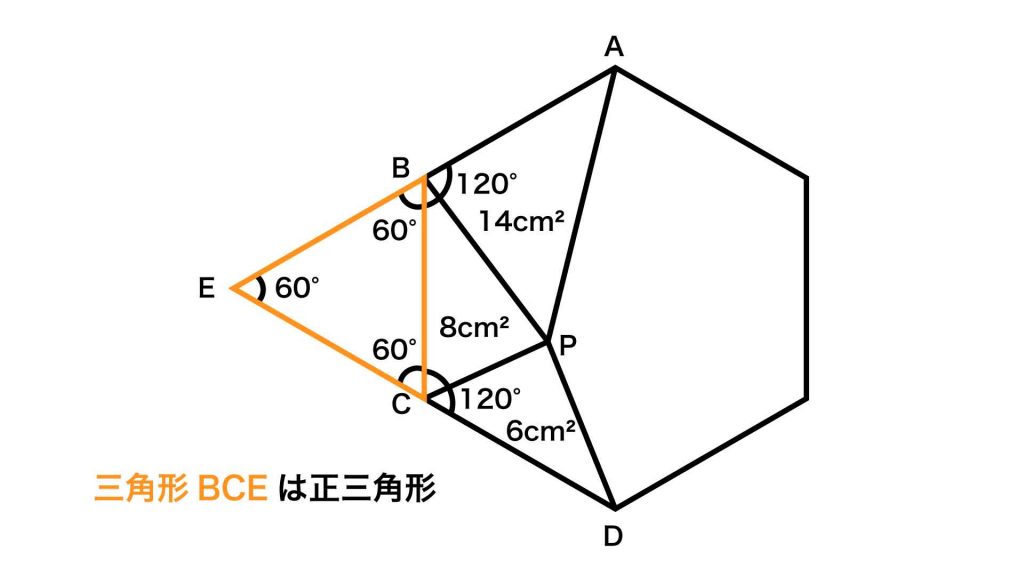
また正六角形には、向かい合う頂点を対角線で結んで六等分すると、各三角形が正三角形になるという性質があります。
三角形BCEの辺BCは正六角形と一辺を共有しているので、三角形BCEは、正六角形を六等分してできる正三角形と合同であることがわかります。
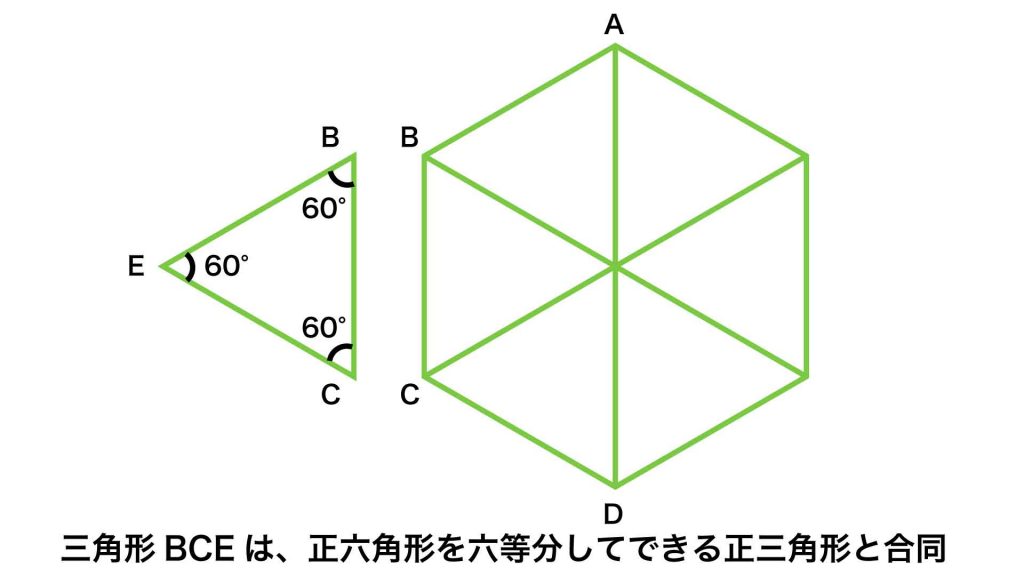
三角形BCEの面積を求める
次に、三角形BCEの面積を求めます。下の図のように、EとPを結ぶ線を引きます。
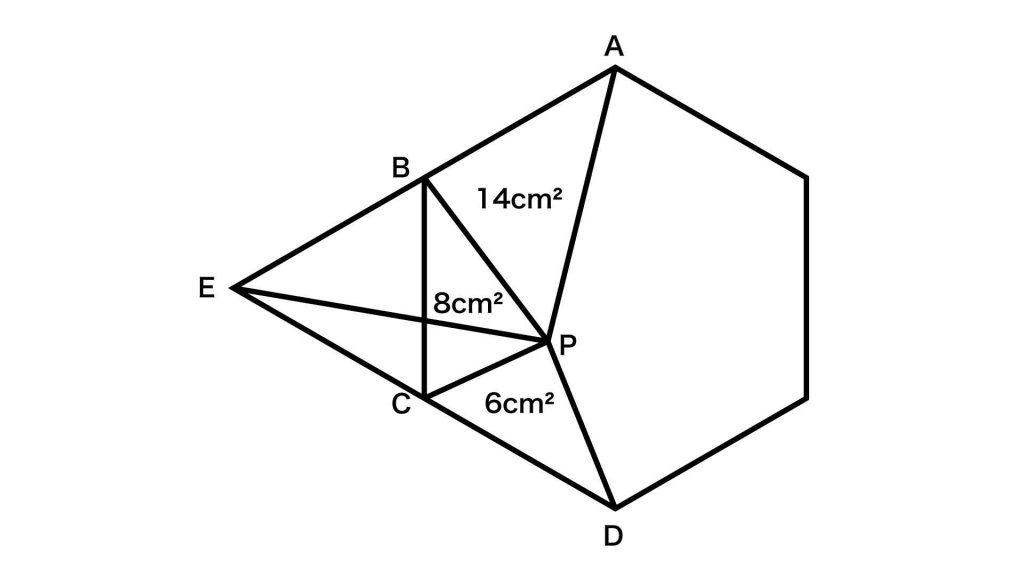
三角形ABPと三角形BEPは、底辺の長さと高さが等しいため、面積は等しくなります。したがって、三角形BEPの面積は14cm2となります。
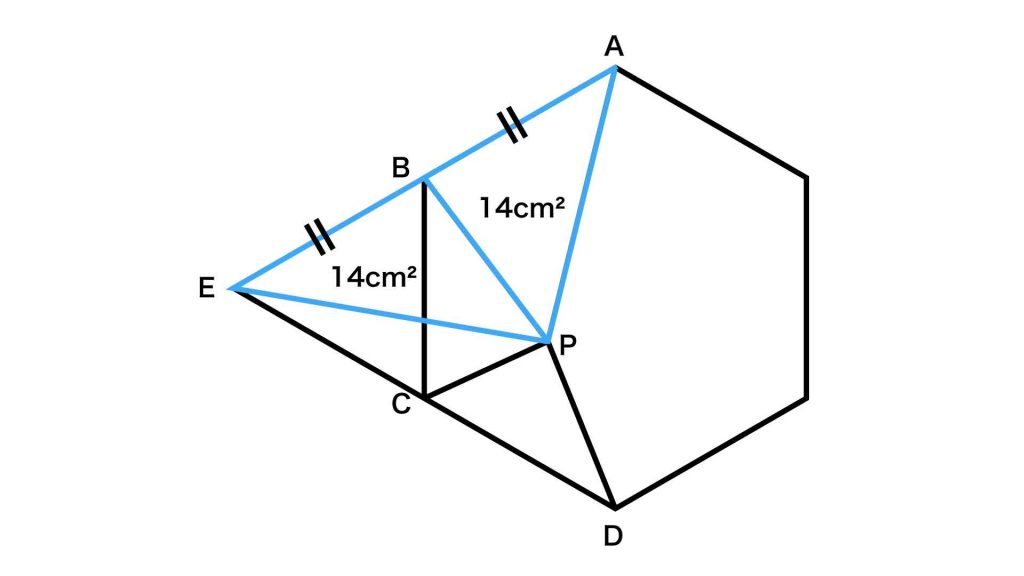
同様にして、三角形CDPと三角形CEPも面積が等しいです。したがって、三角形CEPの面積は6cm2となります。
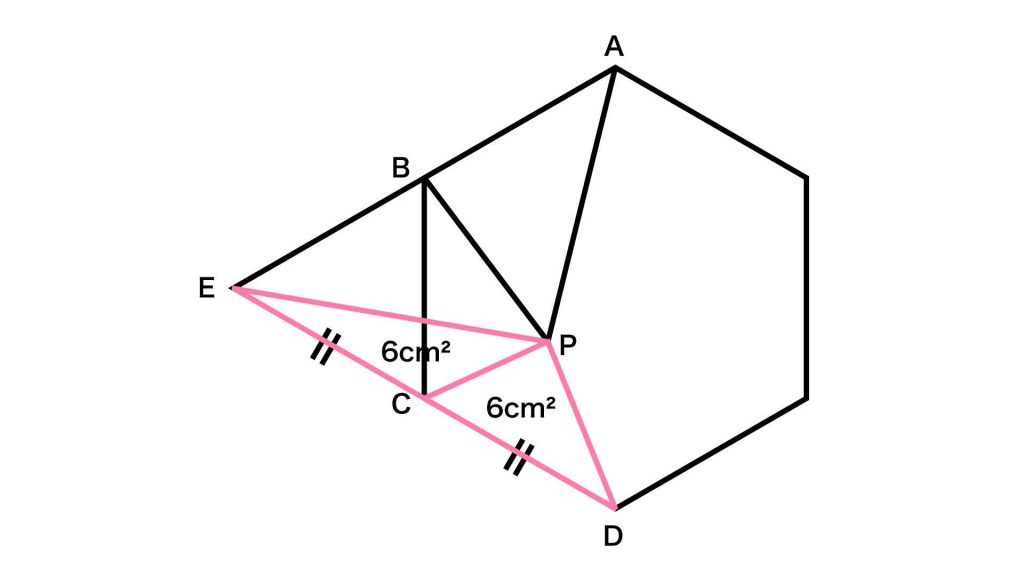
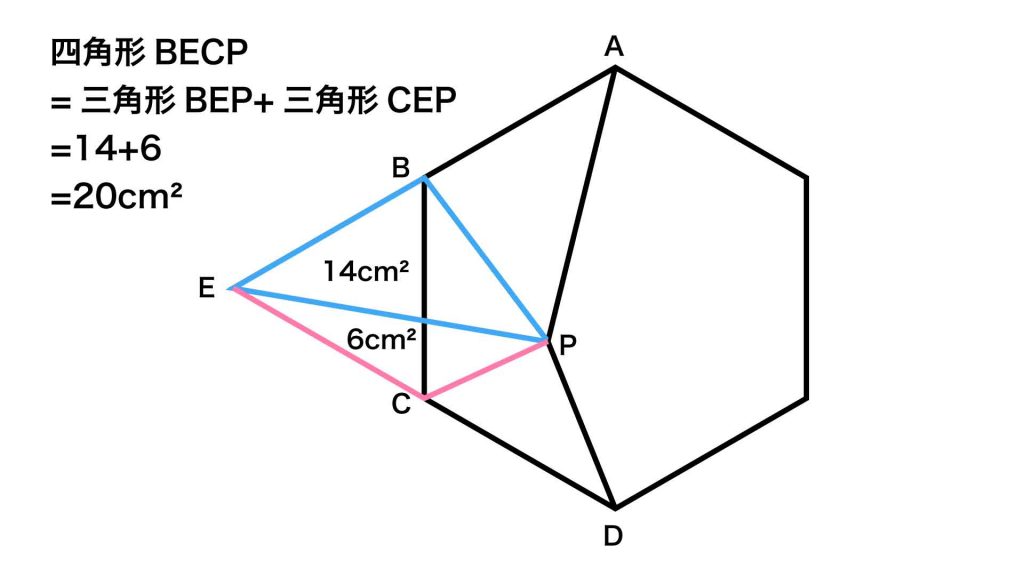
以上より、四角形BECPの面積は、三角形BEPの面積と三角形CEPの面積を足して、14+6=20cm2とわかります。
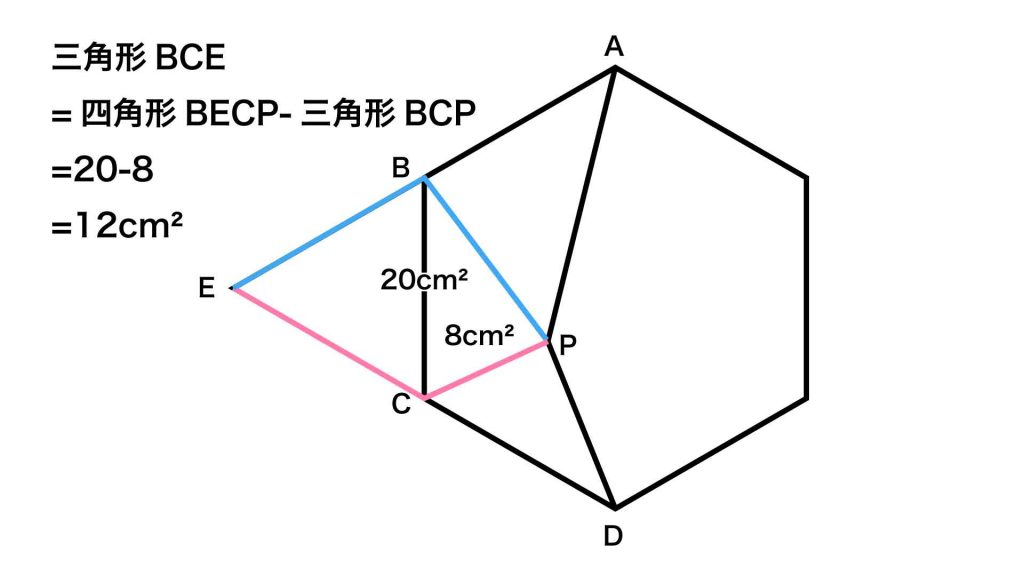
三角形BCEの面積は、四角形BECPの面積から三角形BCPの面積を引くことで求めることができます。三角形BCPの面積は8cm2なので、三角形BECの面積は、20-8=12cm2です。
正六角形は正三角形6つ分
正六角形は、正三角形BECと合同な正三角形6つで構成されています。
したがって、正六角形の面積は、12×6=72cm2となります。
答え:72cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







