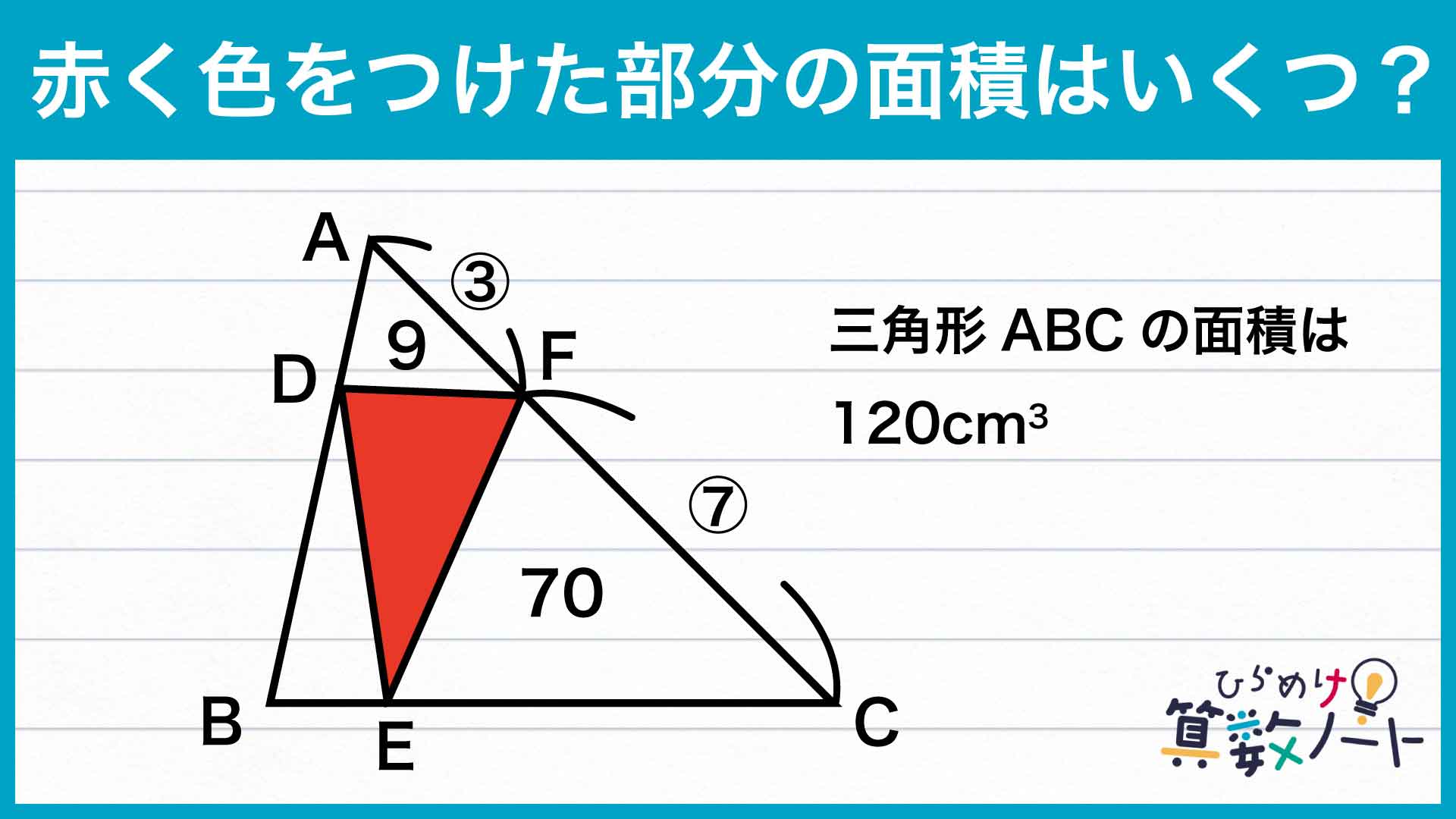
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
この問題を解くうえで重要なポイントをまとめた図がこちらです。
ポイントは「折り返しに着目し、同じ大きさの角度を見つける」ことです。
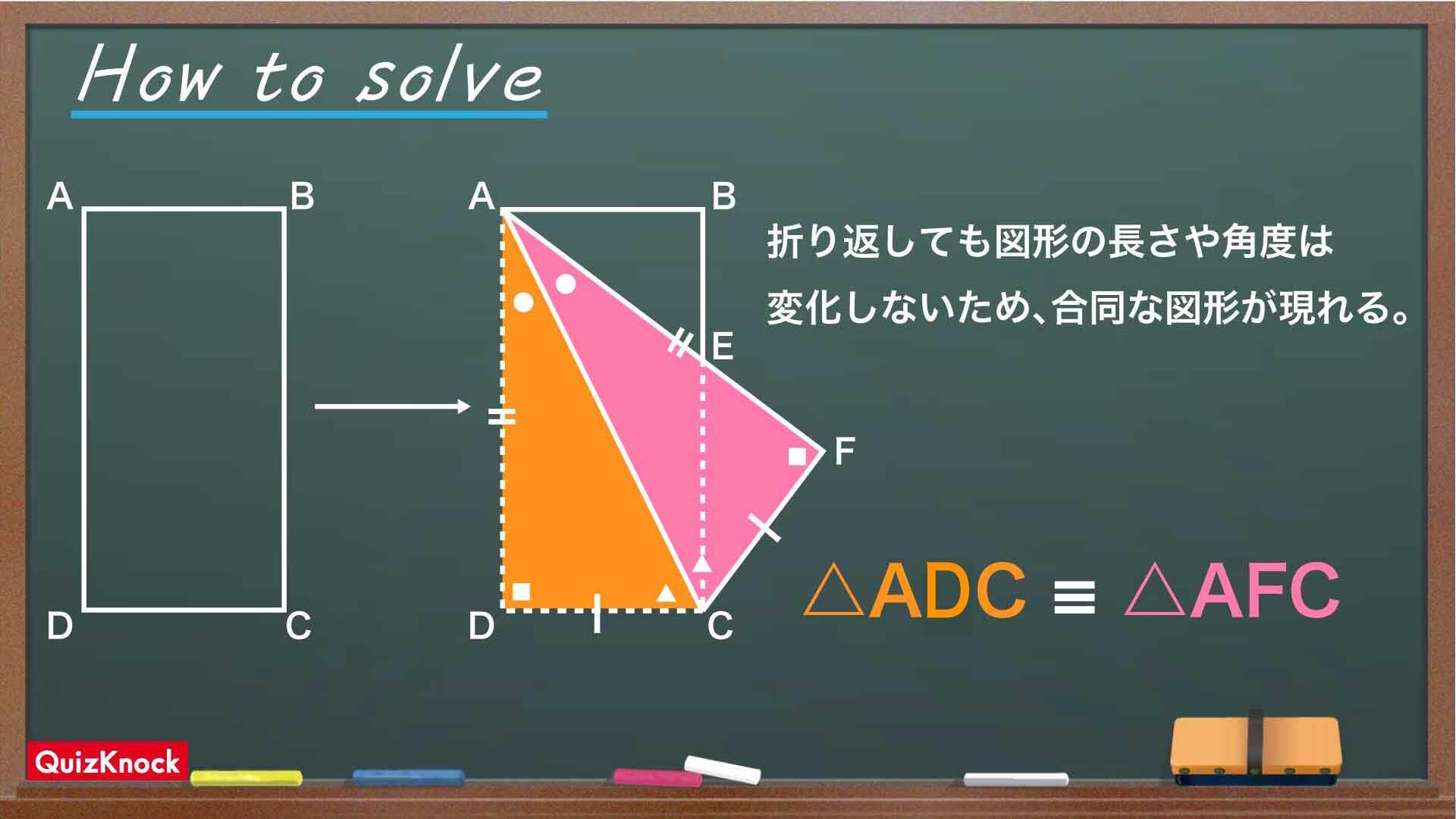
図形を折り返したとしても、「長さ」や「角度」が変化することはありません。つまり、折り返しにより移動した図形は元の位置にあった図形と全く同じ形、つまり合同になります。
そして合同な図形は、同じ大きさの角度を持っています。このことを意識して、解いていきましょう!
合同な図形に注目する
まず、合同な図形を見つけましょう。
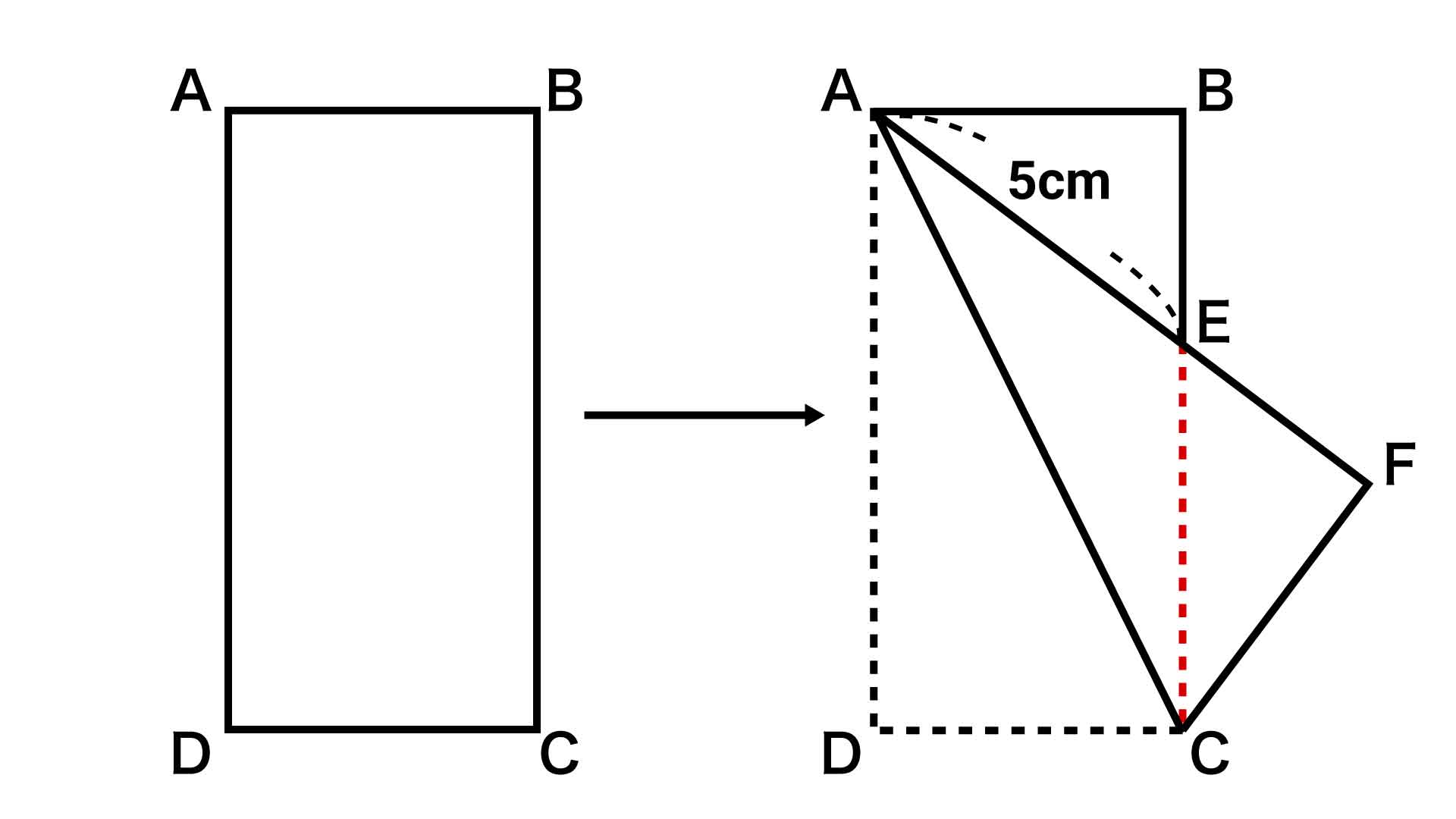
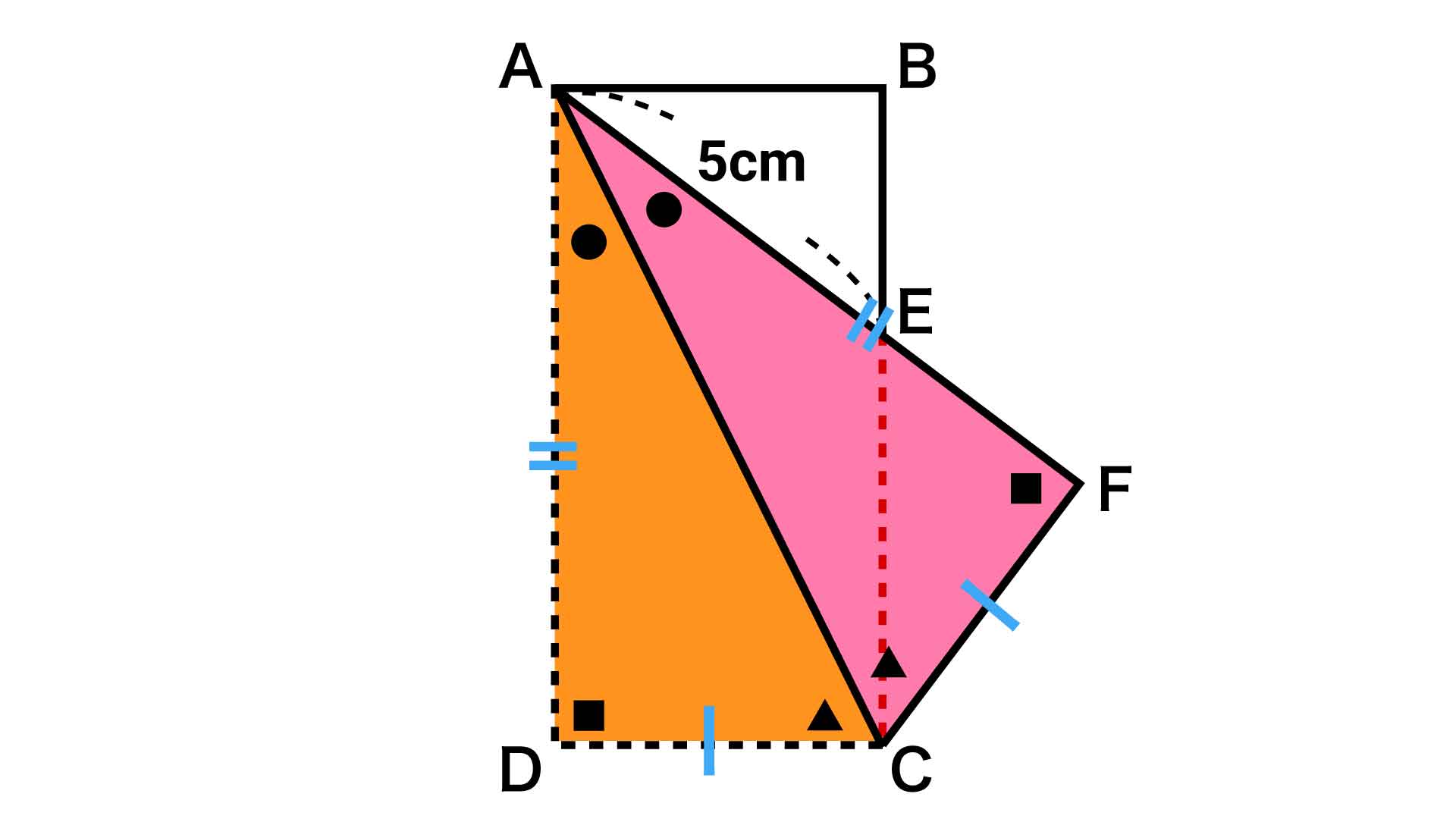
長方形の対角線ACを折り目として、点Dを移動しています。ACは共通であり、AD=AF、CD=CFです。つまり、△ADCと△AFCは合同な図形であることがわかります。
合同な図形において、対応する角度は同じ大きさです。よって、∠DAC=∠FAC(あ)となります。
平行線に注目する
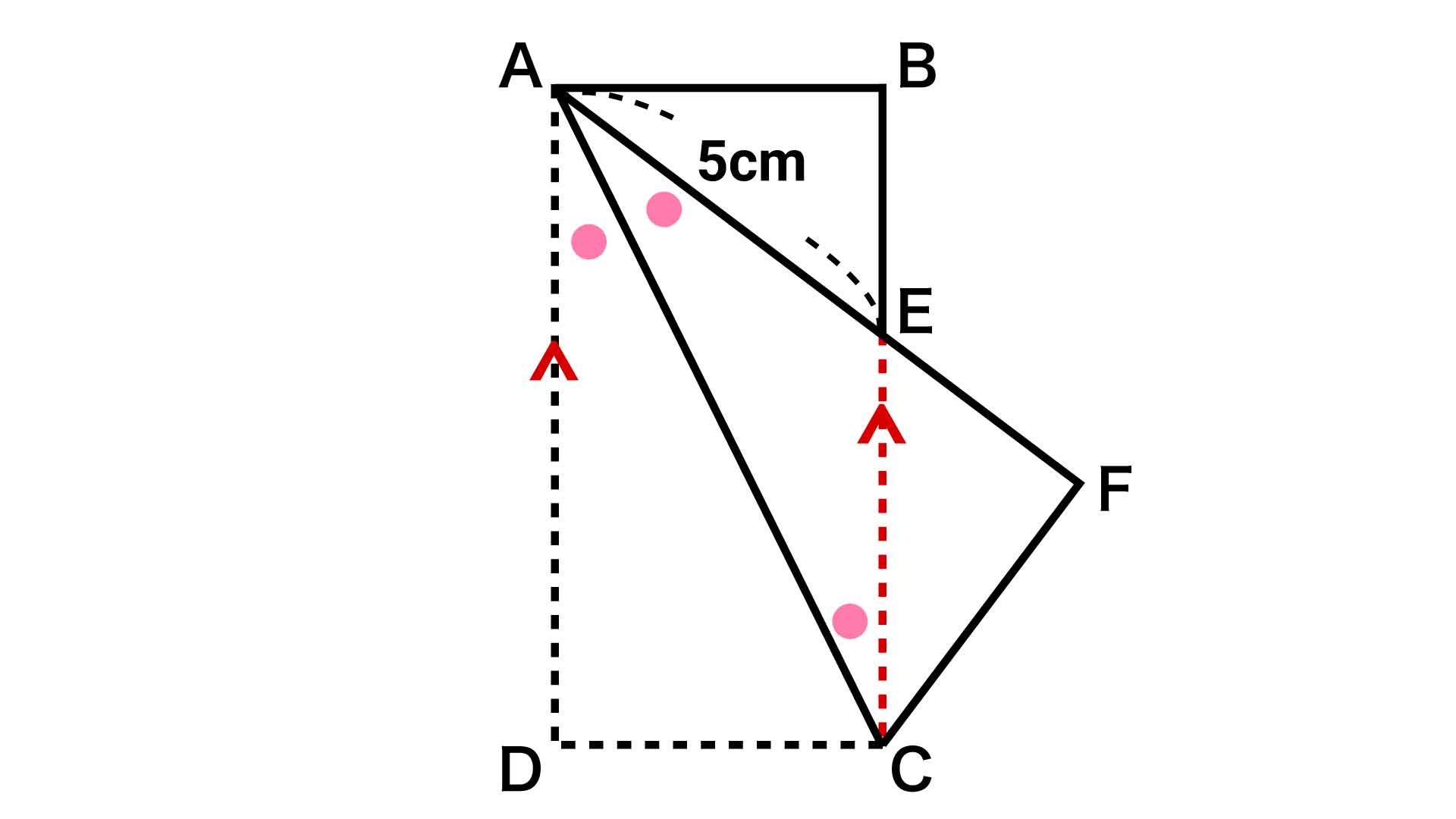
四角形ABCDは長方形なので、辺ADと辺BCは平行です。
平行線における錯角は同じ大きさとなるので、∠DAC=∠BCA(い)となります。
(あ)、(い)より、∠FAC=∠BCAとなります。
あと少し!
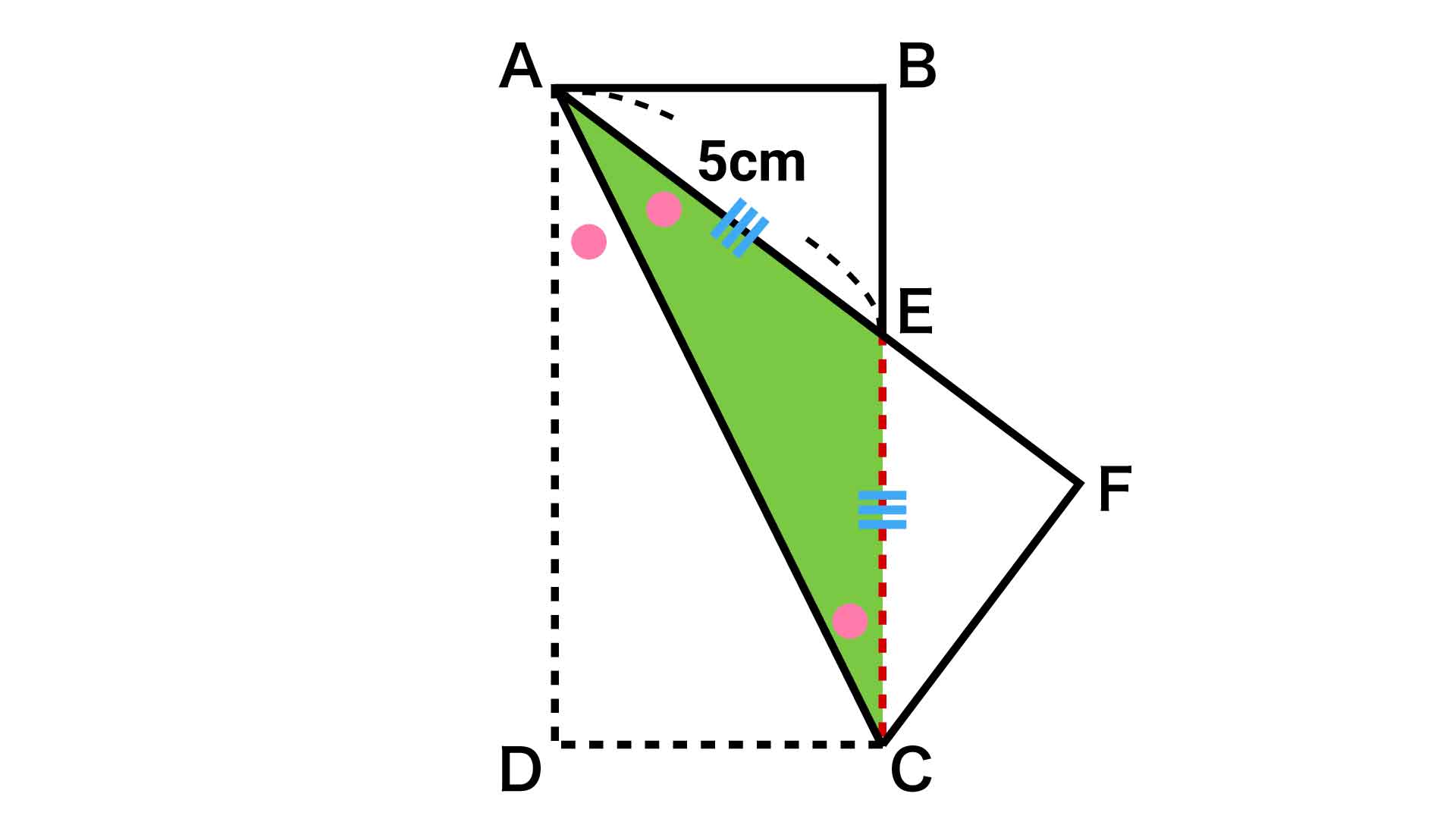
ここで△EACに注目すると、∠EAC=∠ECAとなるので、△EACは、EA=ECの二等辺三角形であることがわかります。
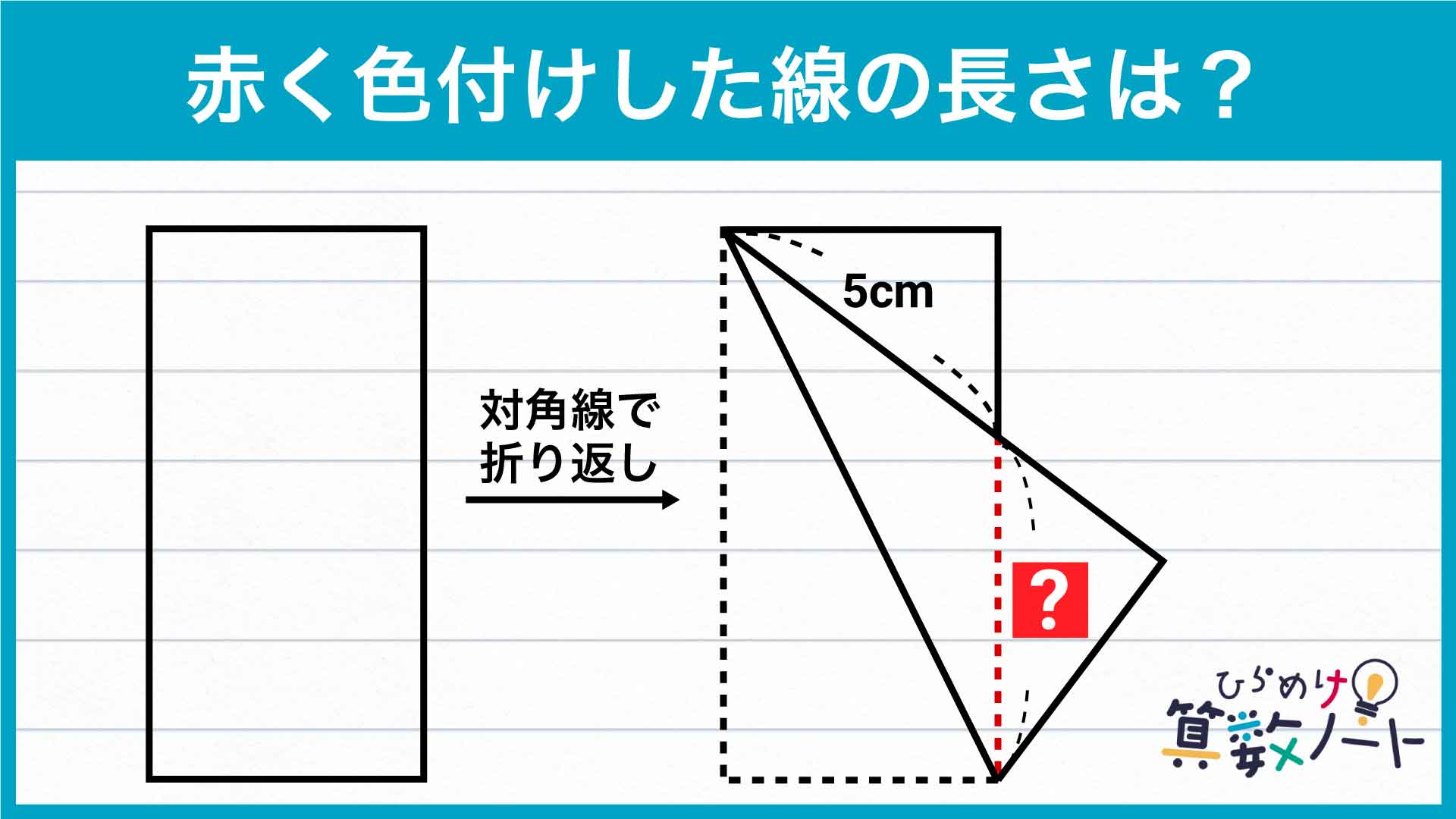
EAの長さは5cmですので、求めるECの長さも5cmとなります。
答え:5cm
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)