解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
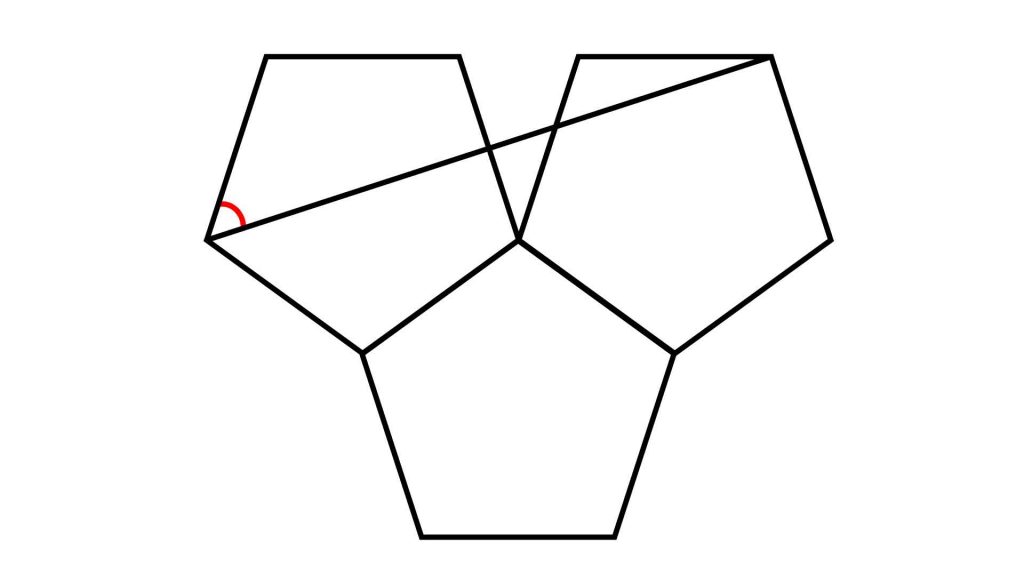
今回のポイントは、「正五角形の内角の性質」を活用することです。これについて、少し細かく見ていきます。
正五角形の内角の性質とは?
下の図のように、正五角形ABCDEに、BとEを結ぶ対角線を引きます。このときAB=AEなので、三角形ABEは二等辺三角形です。
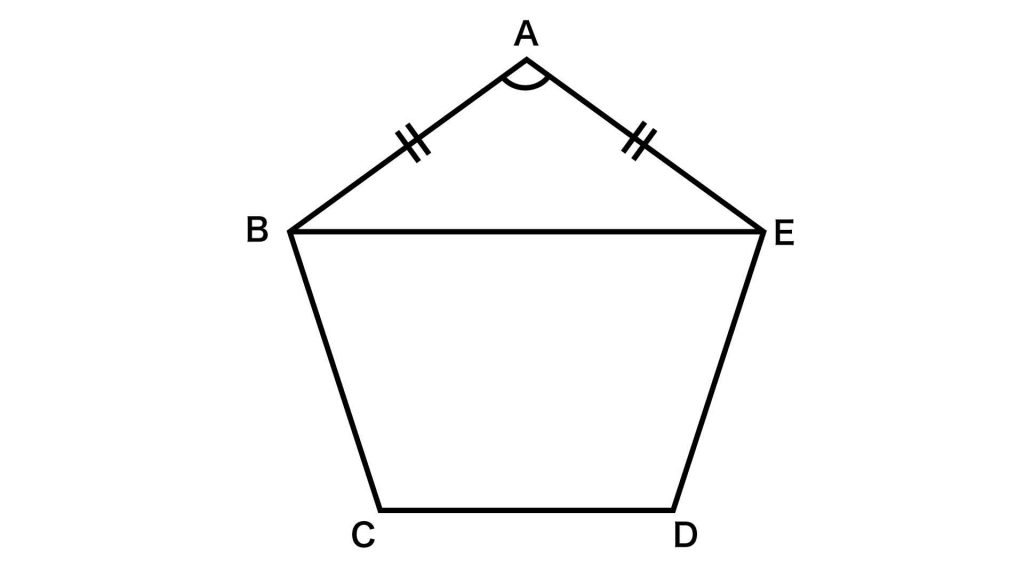
角BAEは正五角形の内角のひとつなので、108度です。したがって、角ABE=(180-108)÷2=36度とわかります。
すると、角EBC=角ABC-角ABE=108-36=72度であることもわかります。
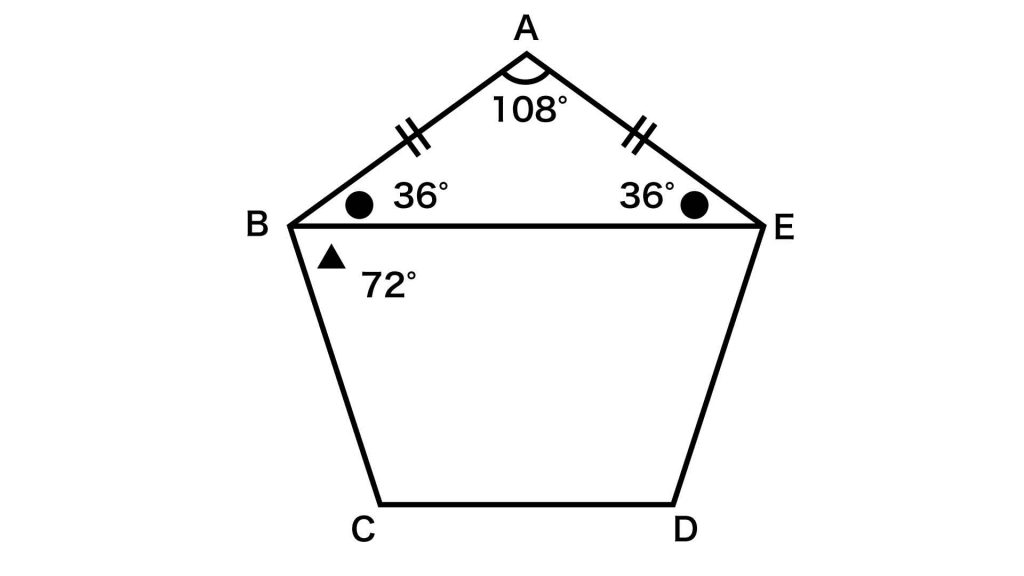
今回の問題では、この角ABE、角EBCとという2つの角の大きさを活用します。
以降、角ABEと同じ大きさをもつ角を●、角EBCと同じ大きさをもつ角を▲とおきます。
補助線を引く
それでは、今回の問題について考えていきます。
まずは、下の図の緑色の線のように、正五角形の内角を結ぶ補助線を引きます。また、各点をA,B,C,D,E,Fとおきます。
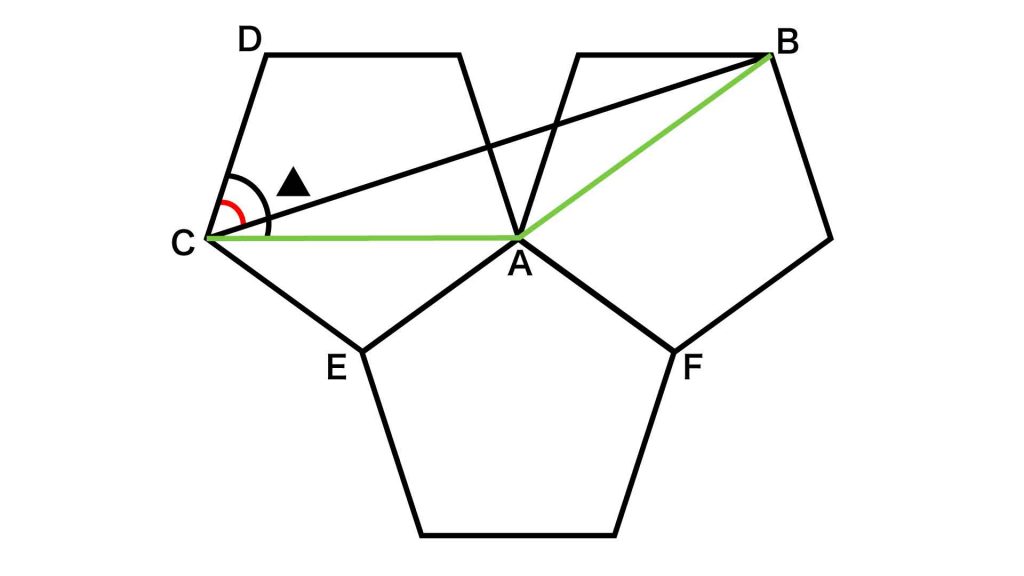
このとき、角ACDの大きさは▲に等しいです。そして、赤く色を付けた角の大きさは、角ACDから角ACBの大きさを引くことで求めることができます。
したがって、角ACBの大きさがわかれば、赤い印をつけた角の大きさがわかります。
さらに、三角形ABCはAB=ACの二等辺三角形なので、角BACの大きさがわかれば、角ACBの大きさを求めることができます。
角BACの大きさを求める
角BACの大きさは、360度から、角CAE、角EAF、角FABの大きさを引くことで求めらます。
まず、角CAEは角●に等しいので、36度です。
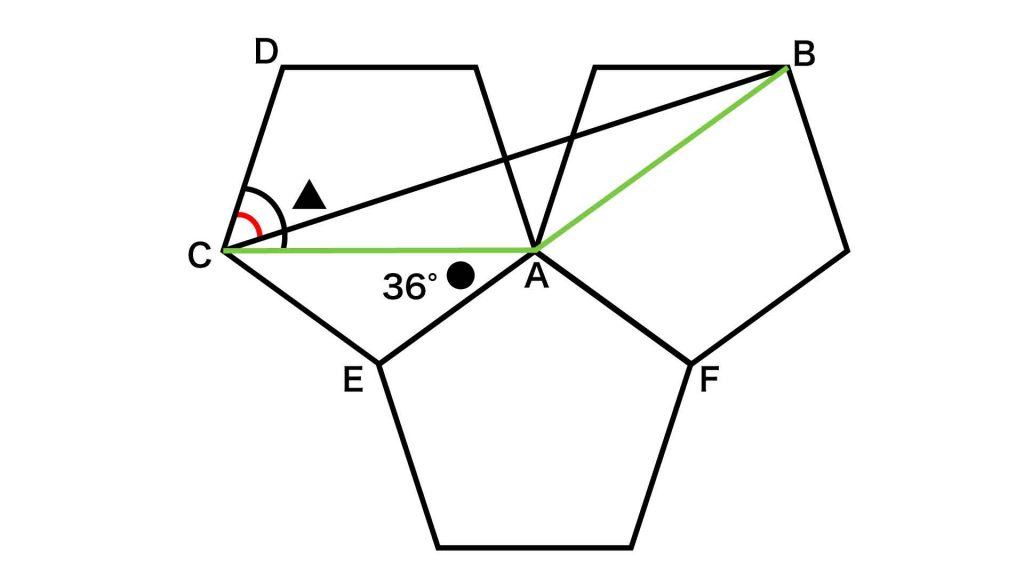
次に、角EAFは正五角形の内角なので、108度です。
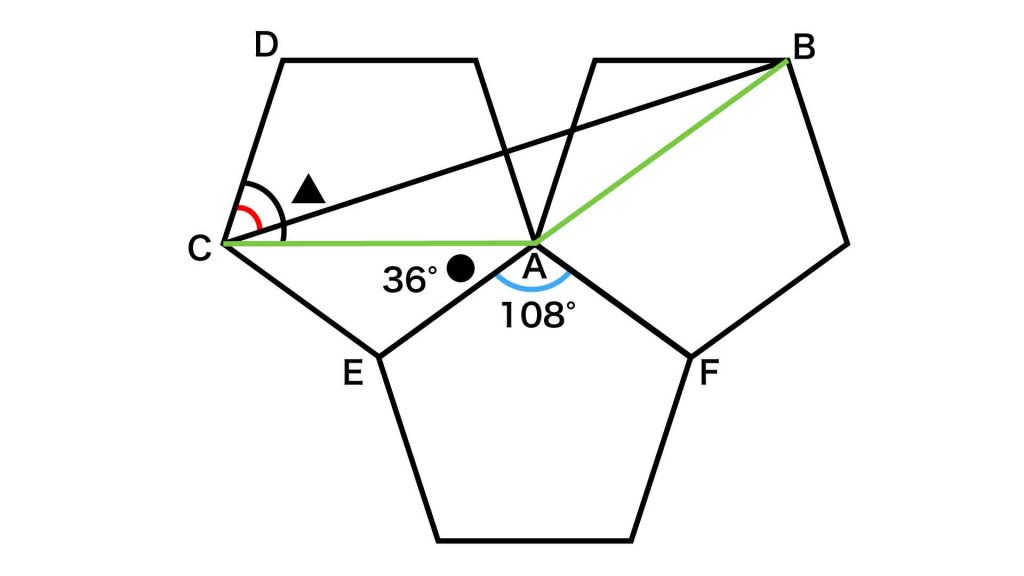
最後に、角FABは角▲に等しいので、72度となります。
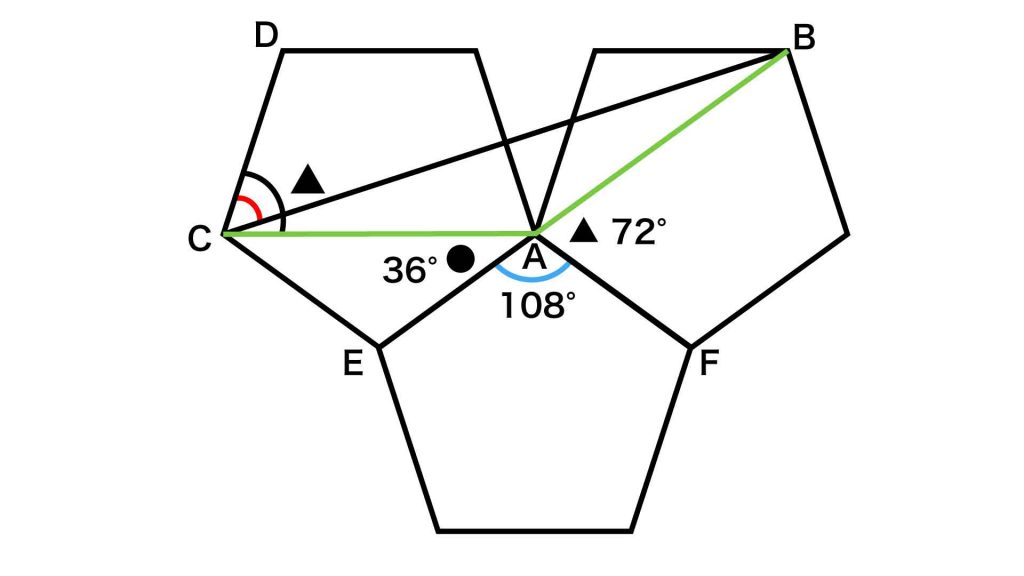
したがって、角BACの大きさは、360-(108+36+72)=144度と求めることができます。
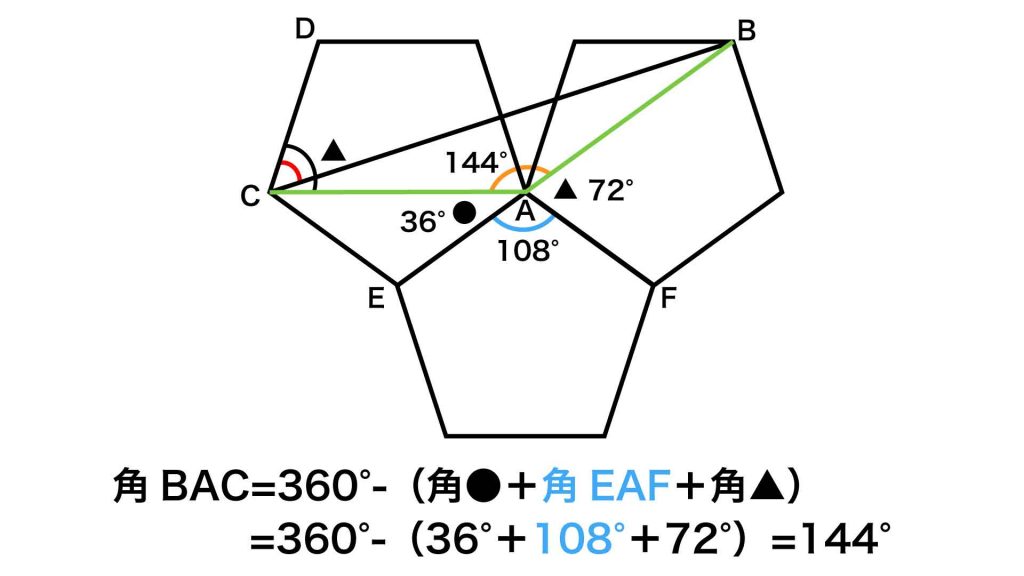
角ACBの大きさを求める
三角形ABCは、AB=ACの二等辺三角形でした。
したがって、角ACBの大きさは、(180-144)÷2=18度となります。
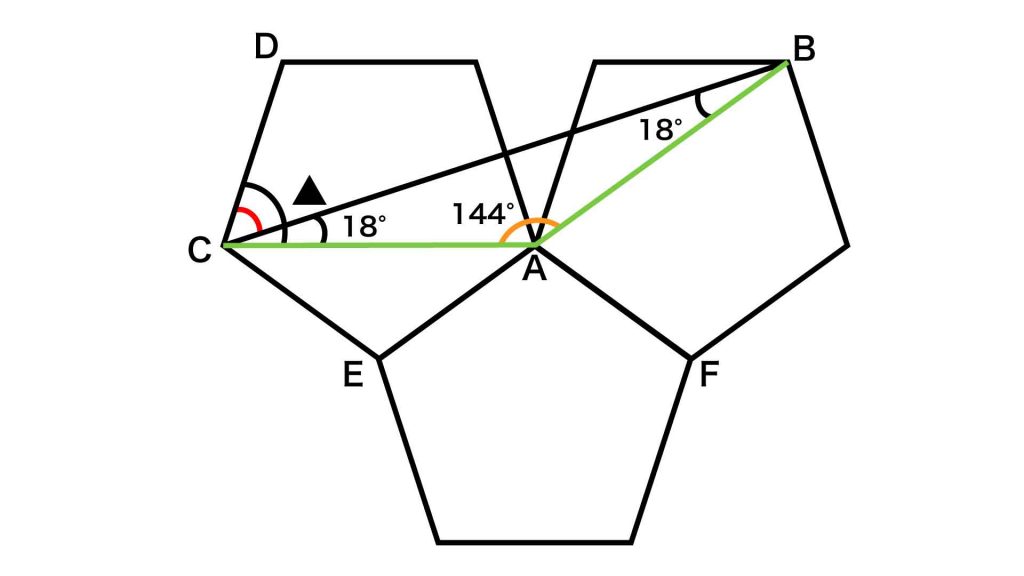
求める角=角▲-角ACB
角ACDの大きさは▲と等しいので、72度です。
よって、赤く色を付けた角の大きさは、72-18=54度となります。
答え:54度
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







