解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
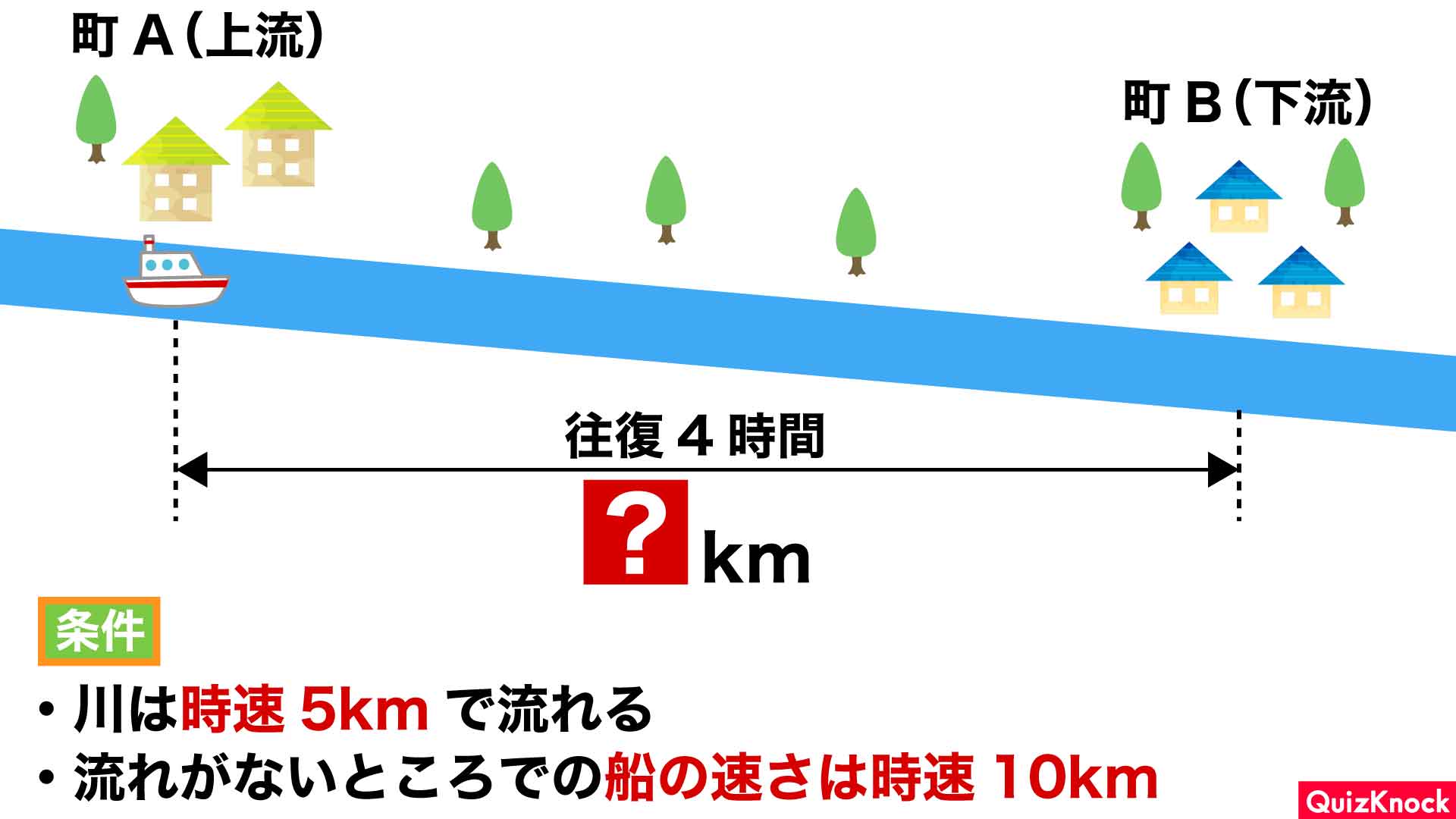
この問題を解くうえで重要なポイントをまとめた図がこちらです。
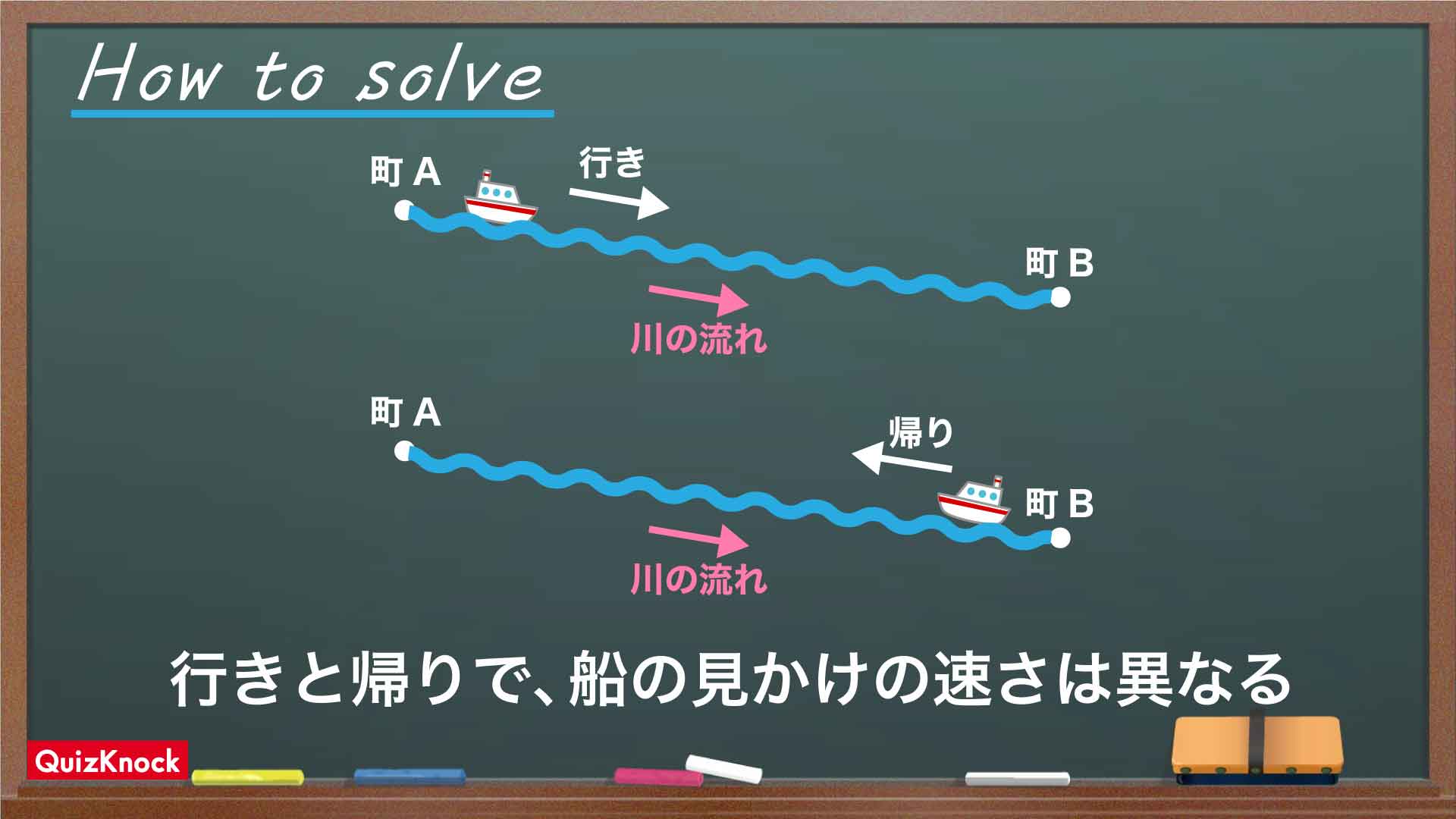
ポイントは「川の流れを考え、船の見かけの速さが往路と復路で異なる」ことです。
ここで登場する「見かけの速さ」とは「川岸に停止している人から見る船の速さ」のことです。船自体の速さは時速10kmで一定です。しかし、上流の町Aから下流の町Bに行く往路では川の流れの分、船の見かけの速さは増加します。反対に町Bから町Aに帰るときは、船の見かけの速さは減少します。
このことを意識して、解いていきましょう!
川の流れを考え、船の見かけの速さを求める
まず、流れのない水面を、船が時速10kmで進んでいる場合を考えます。このとき、船の見かけの速さは時速10kmです。
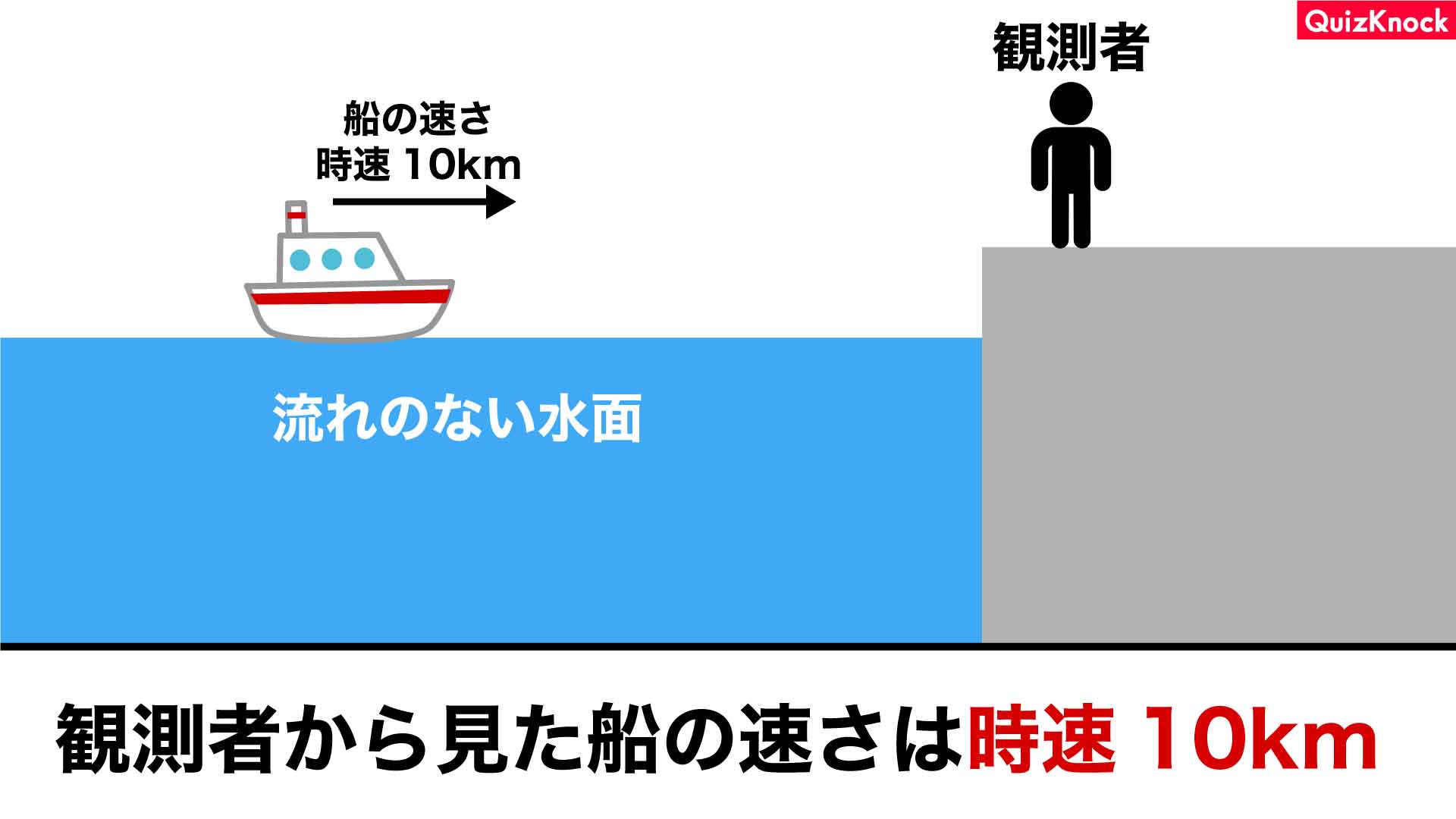
次に、時速5kmで流れる川の水面に、エンジンを切って停止している船が浮かんでいるところをイメージしてみてください。船自体は動いていませんが、川の流れに身を任せるため、船の見かけの速さは時速5kmとなります。
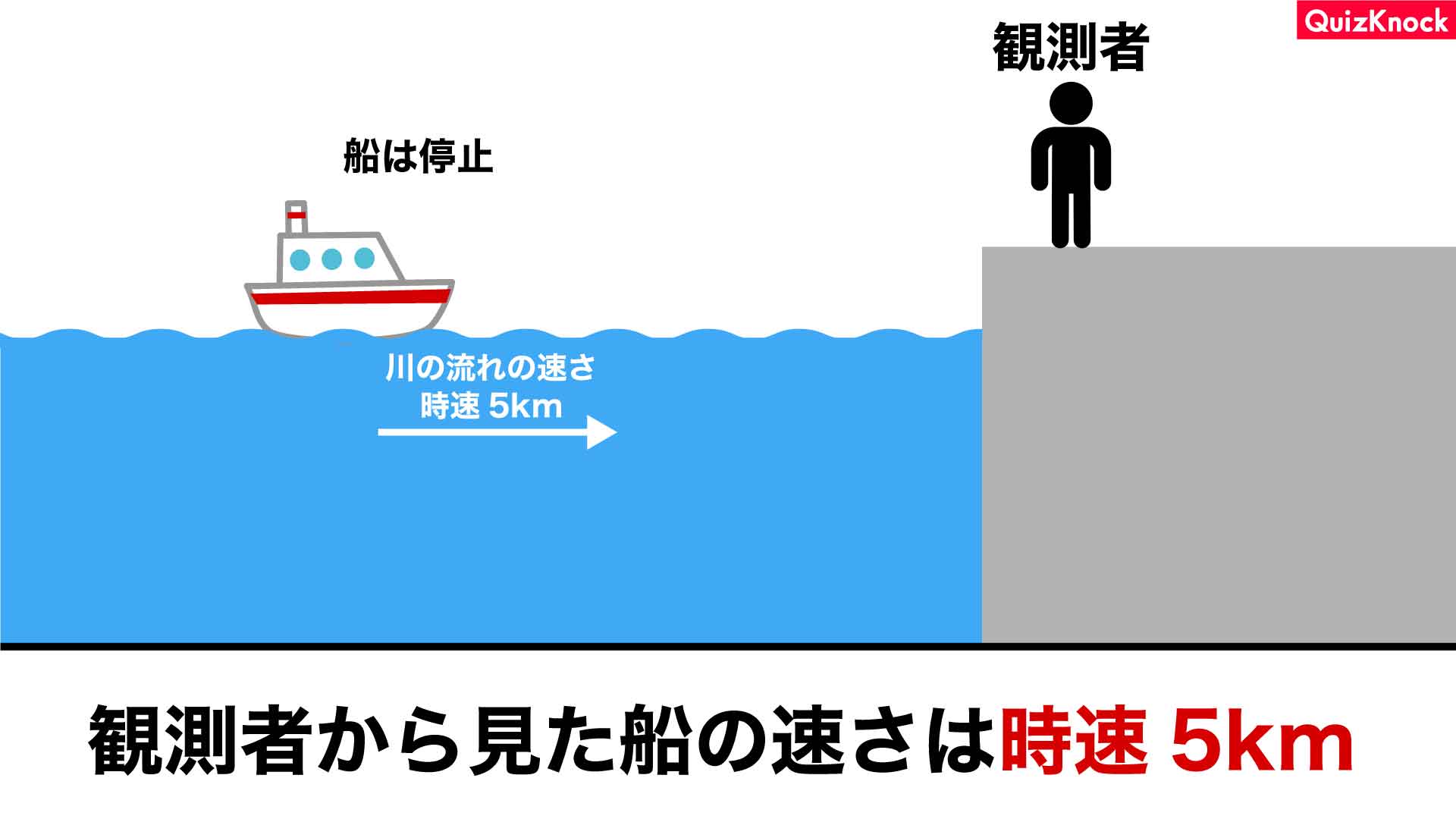
今回の問題では、この2つの状況の足し合わせとなります。
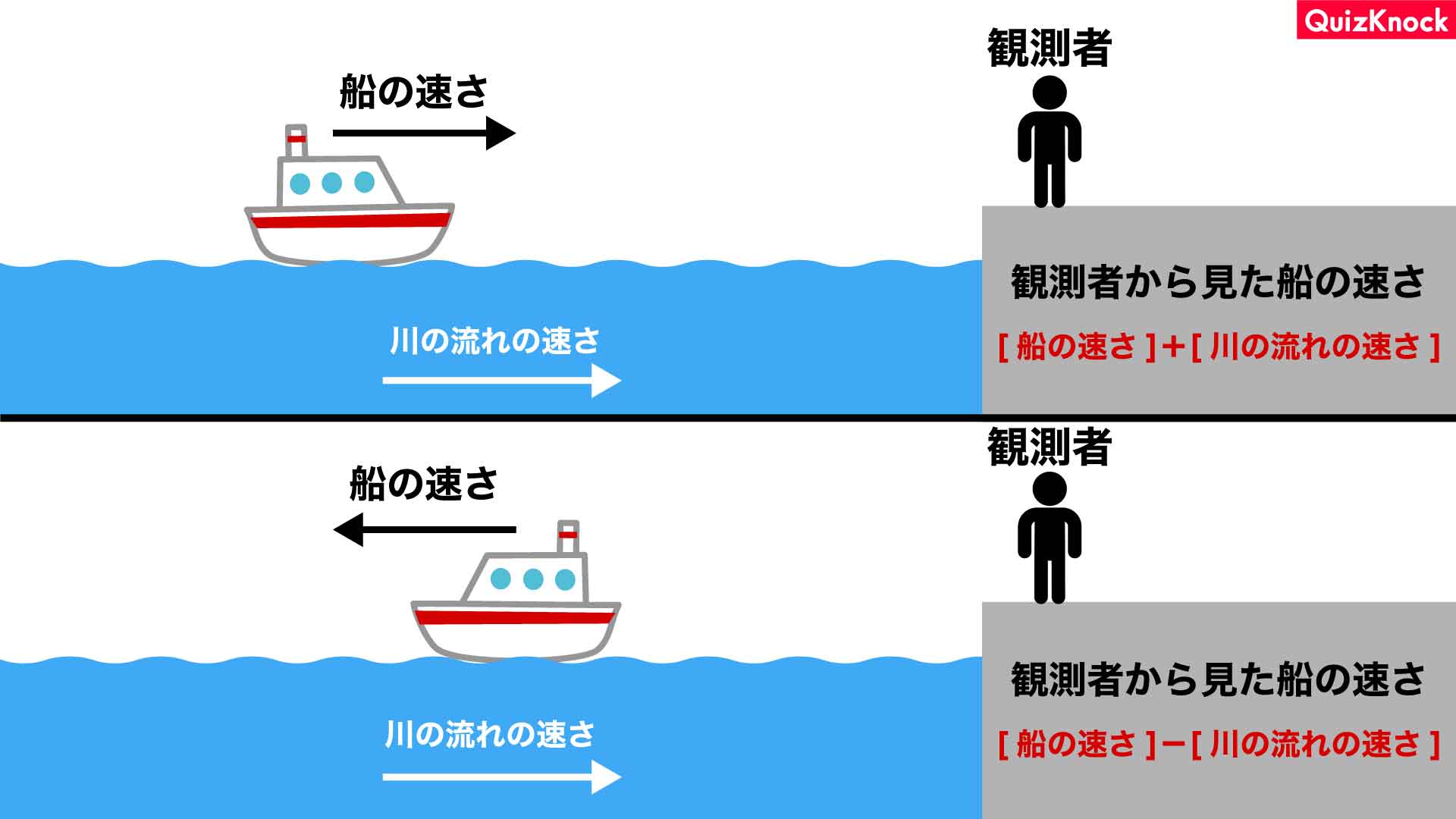
すなわち、川の流れと同じ方向に船が進むとき、船の速さに川の流れの速さが上乗せされます。
反対に、川の流れと逆の方向に船が進むとき、船の速さは川の流れの速さにより打ち消されます。
以上の考え方を、問題に適用させましょう。
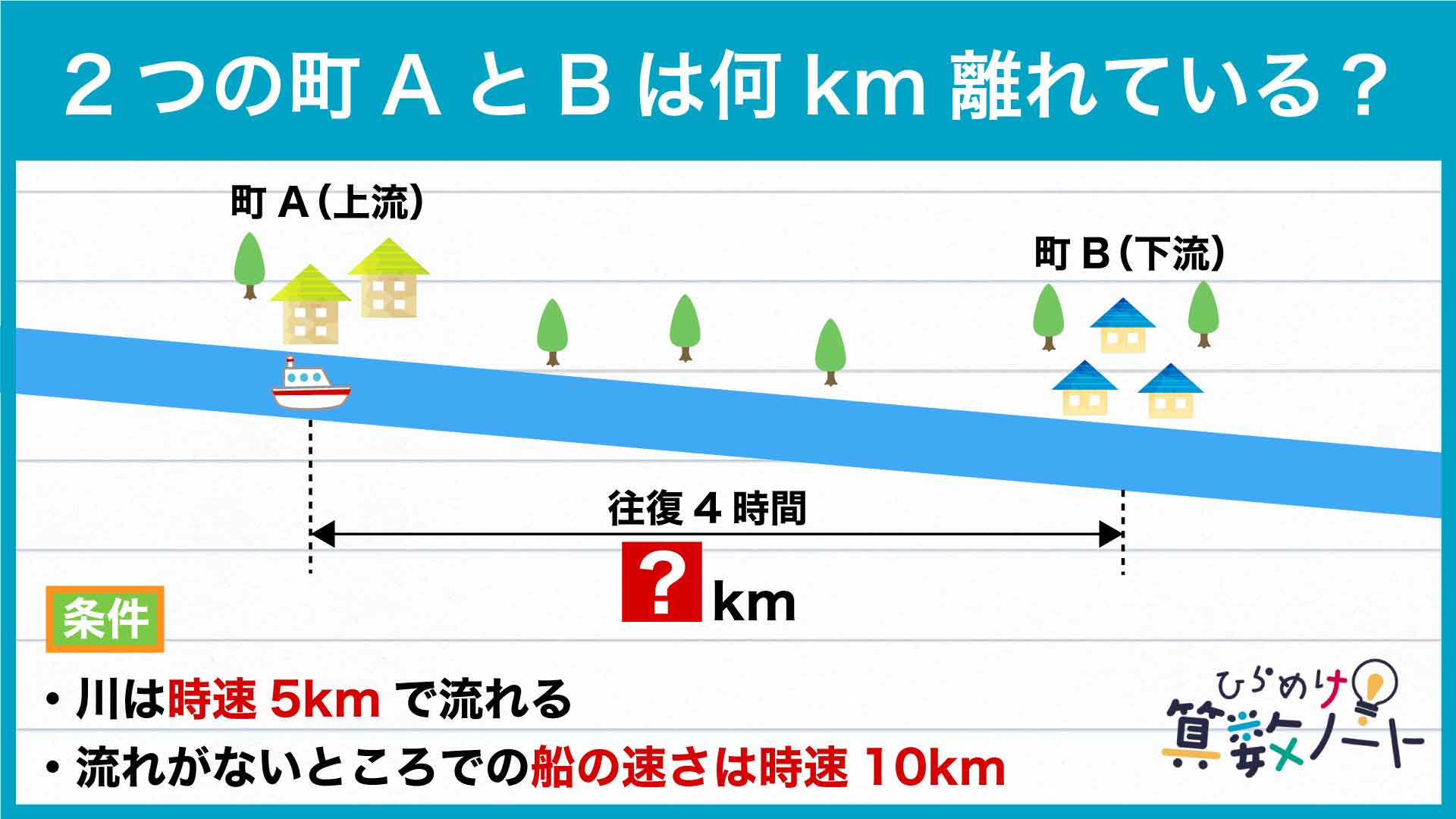
 ▲問題はこちらでした
▲問題はこちらでした
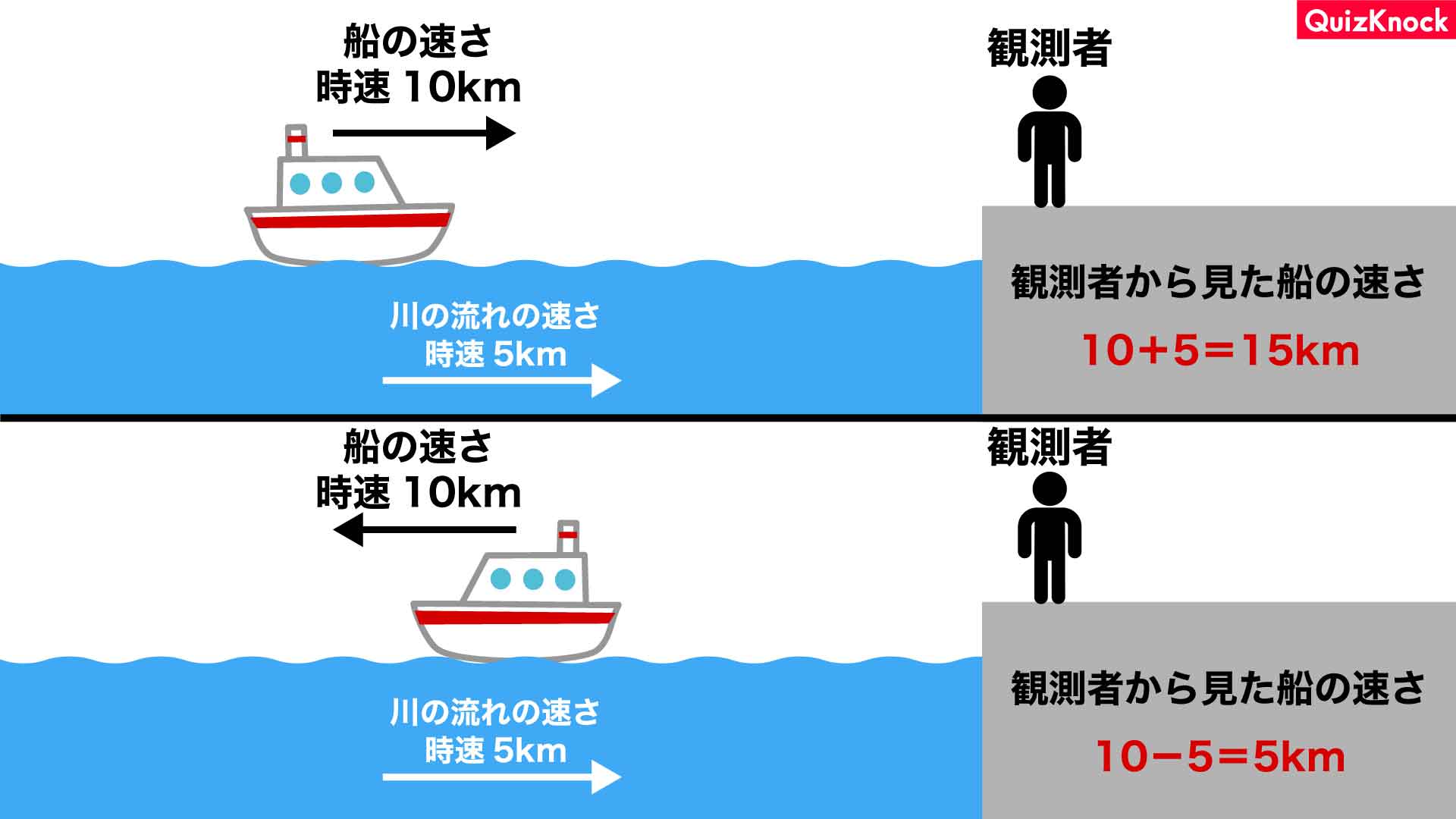
町Aから町Bに行くときは、船の進む方向と川の流れが同じです。
よって、船の見かけの速さは、10+5=15より、時速15kmとなります。
一方、町Bから町Aに帰るときは、船の進む方向と川の流れが逆です。
よって、船の見かけの速さは、10-5=5より、時速5kmとなります。
往復でそれぞれかかった時間を求める
時間に関しては「往復で4時間かかった」ということだけがわかっています。
ここから、船の行きと帰りの速さの比を使って、それぞれの移動に何時間かかったかを求めていきます。時間を求めるにあたり、以下の重要な性質を使います。
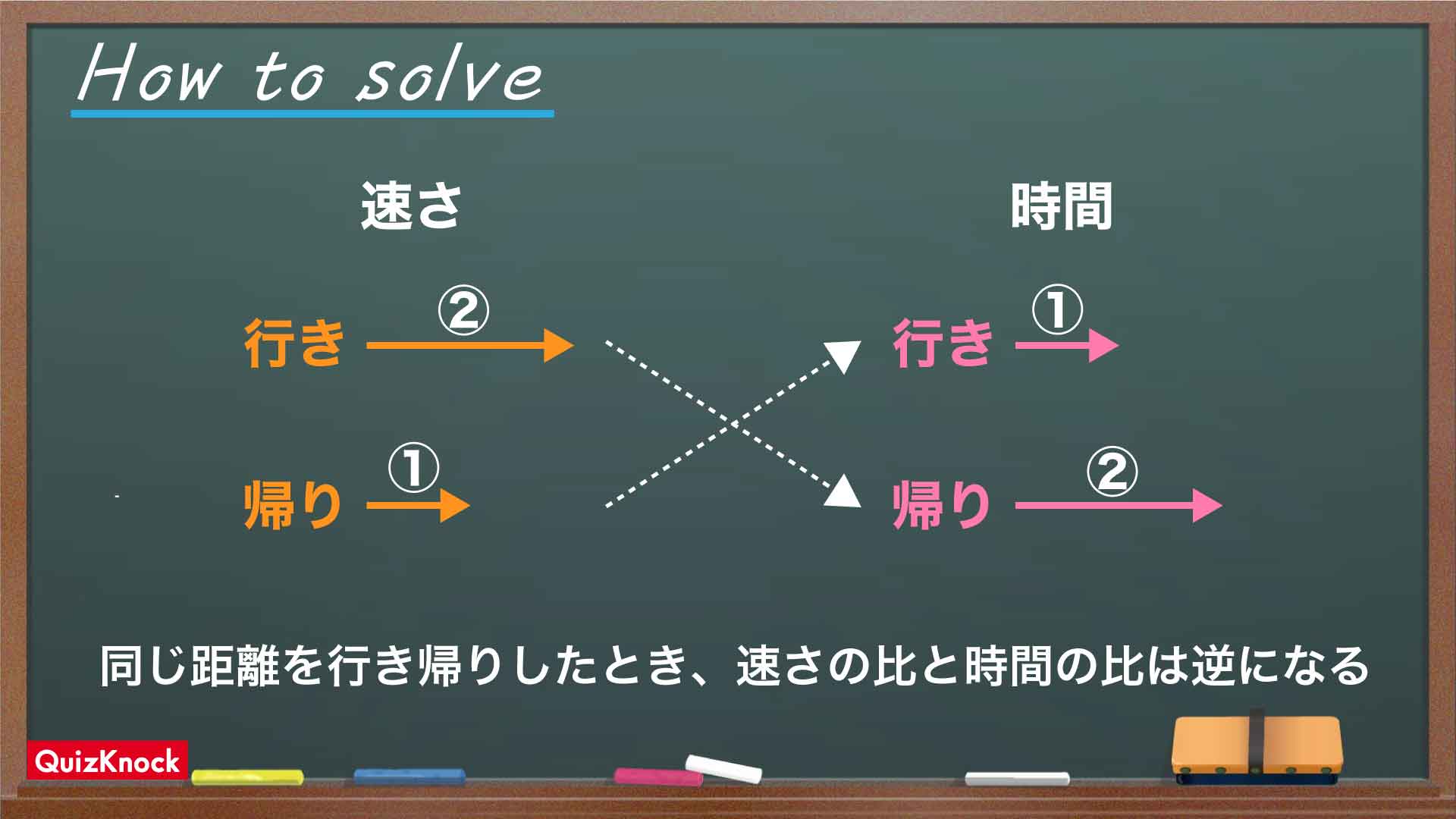
例えば、6kmの道のりを、行きは時速2km、帰りは時速1km(速さの比は2:1)で移動するとします。このとき、行きは6÷2=3時間、帰りは6÷1=6時間かかることから、時間の比は1:2となり、速さの比の逆であることがわかります。
以上の関係性を、今回の問題にも適用します。
船の行きの時速が15km、帰りの時速が5kmなので、速さの比は3:1です。移動する距離は行きと帰りで変わらないため、移動にかかる時間の比は、速さの比の逆をとって1:3となります。

船が町Aから町Bまで行くのにかかった時間は、船が往復するのにかかった時間の1/4です。往復にかかった時間は4時間ですから、行きにかかった時間は4×(1/4)=1時間となります。
町Aと町Bの距離を求める
最後に距離を求めます。速さと時間がわかっているので、この2つを掛け合わせると距離を求めることができます。
したがって距離は、15×1=15より15kmとなります。
答え:15km
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)










.jpg)







