問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ!以下は問題の解説です
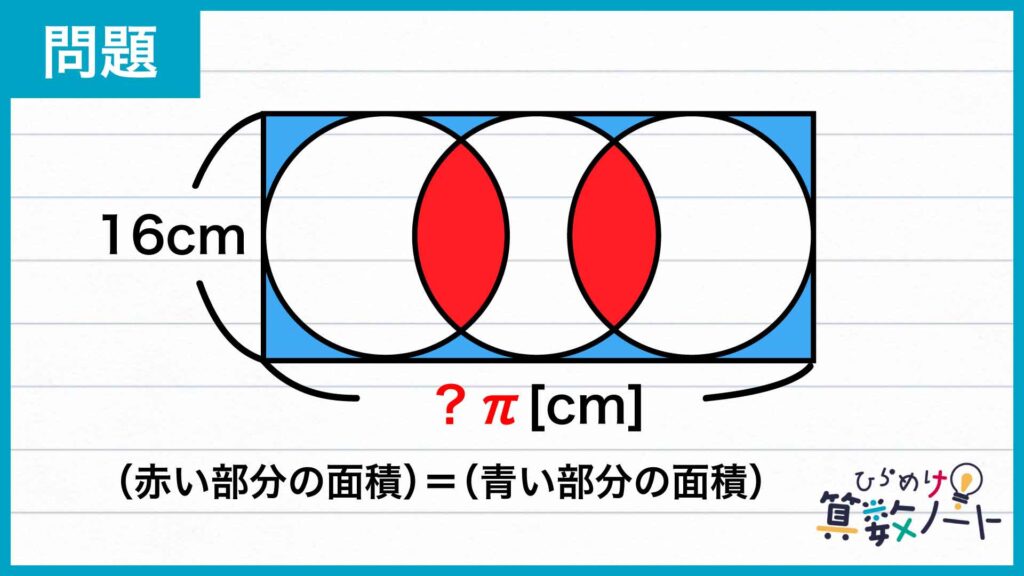
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつをご紹介します。
今回の問題の解き方をまとめた図がこちらになります。
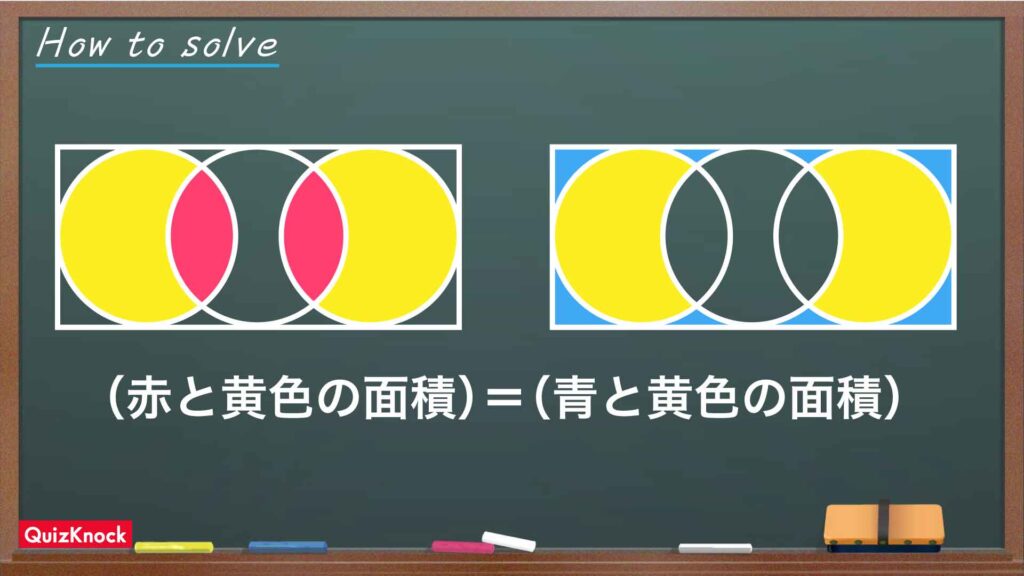
ポイントは、面積が等しい関係性と円の面積を利用することです。これを踏まえて解いていきましょう!
長方形の面積を求める
最終的に求めたい長方形の横の長さは、長方形の面積がわかれば、縦の長さの16cmで面積を割ることで求めることができます。
3つの円は長方形に内接しているため、円の直径は長方形の縦の長さと同じ16cmです。これで円の面積は求められます。
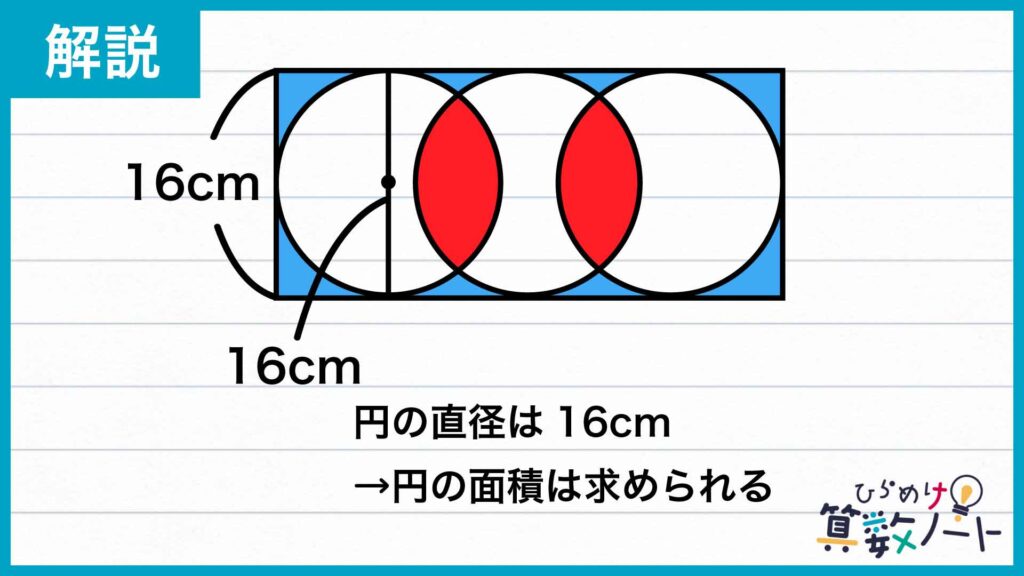
では、長方形の面積はどのようにして求めれば良いでしょうか?
面積が等しい関係に注目する
問題の「赤い部分の面積の和=青い部分の面積の和」という関係を利用しましょう。
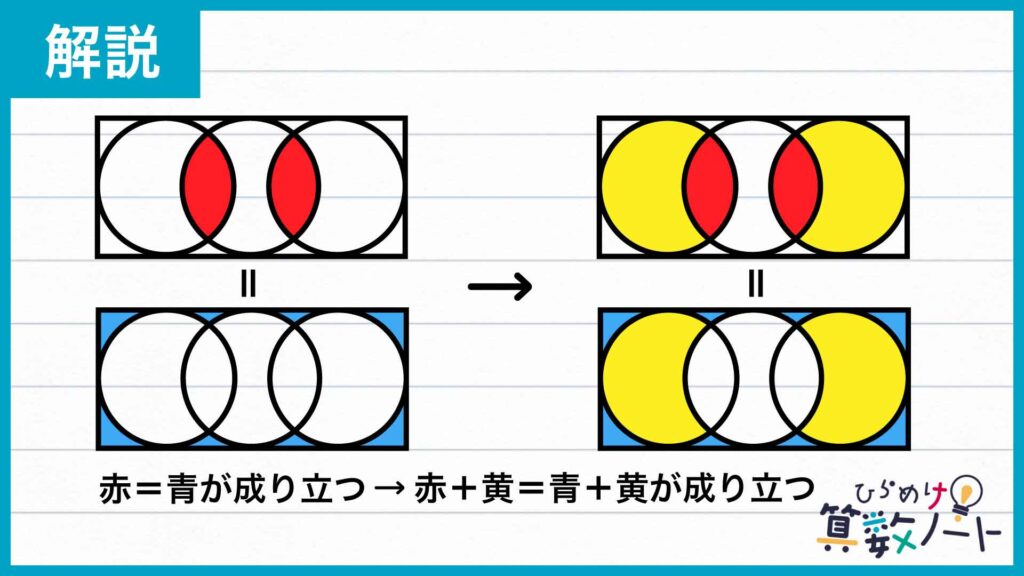
例えば、 A=B が成り立つとき A+C=B+C も成り立つように、「赤い部分の面積の和」と「青い部分の面積の和」の両方に同じ面積の和を足しても、面積が等しい関係が成り立ちます。
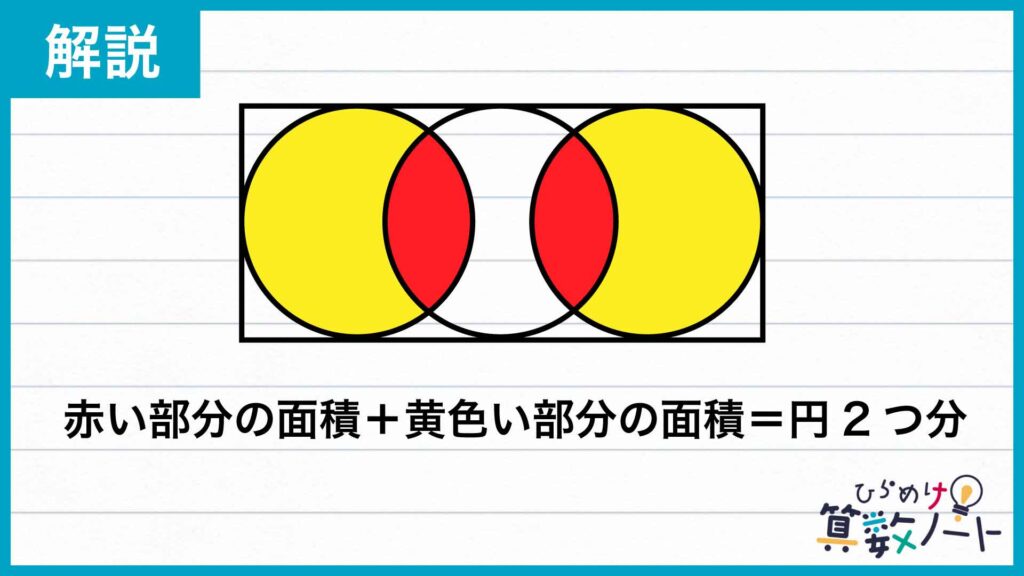
問題の「赤い部分の面積の和」と黄色の部分の面積の和は円2つ分の面積なので、 (8×8×π)×2=128πcm² です。
「青い部分の面積の和」は「赤い部分の面積の和」と等しいため、以下の「青い部分の面積の和」と黄色の部分の面積の和も 128πcm² になります。
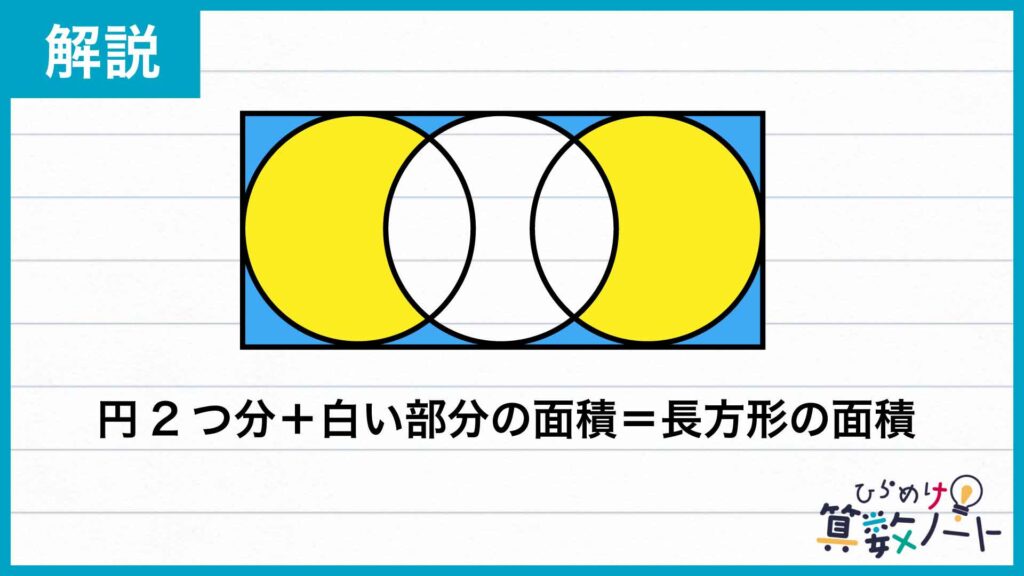
最後に残った白い部分の面積をあわせると長方形の面積は、 128π+(8×8×π)=192πcm² と求められます。
よって、求めたい長方形の横の長さは、192π÷16=12πcm になります。
答え:12πcmそれではまた次の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】