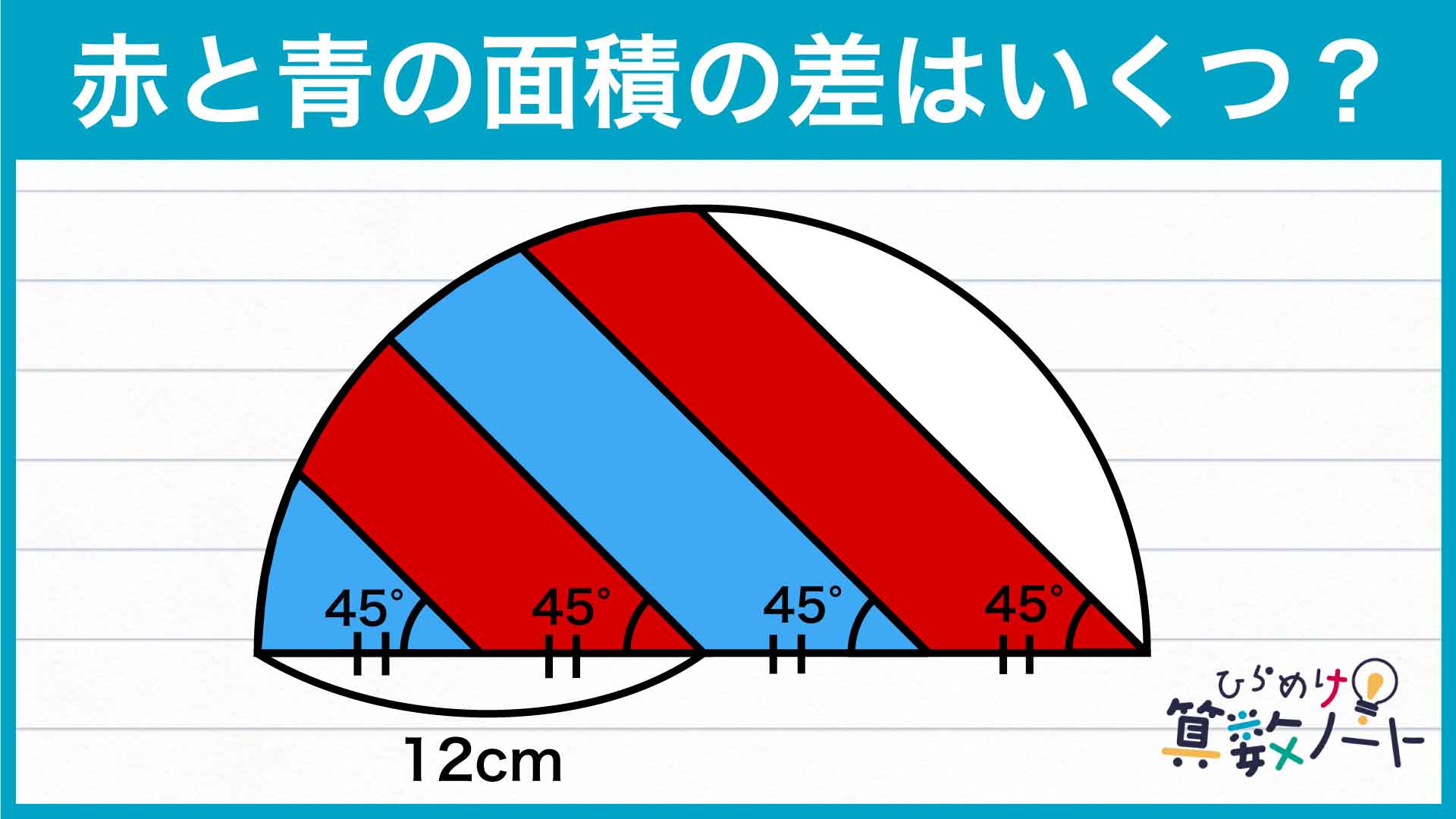
【問題はこちら】
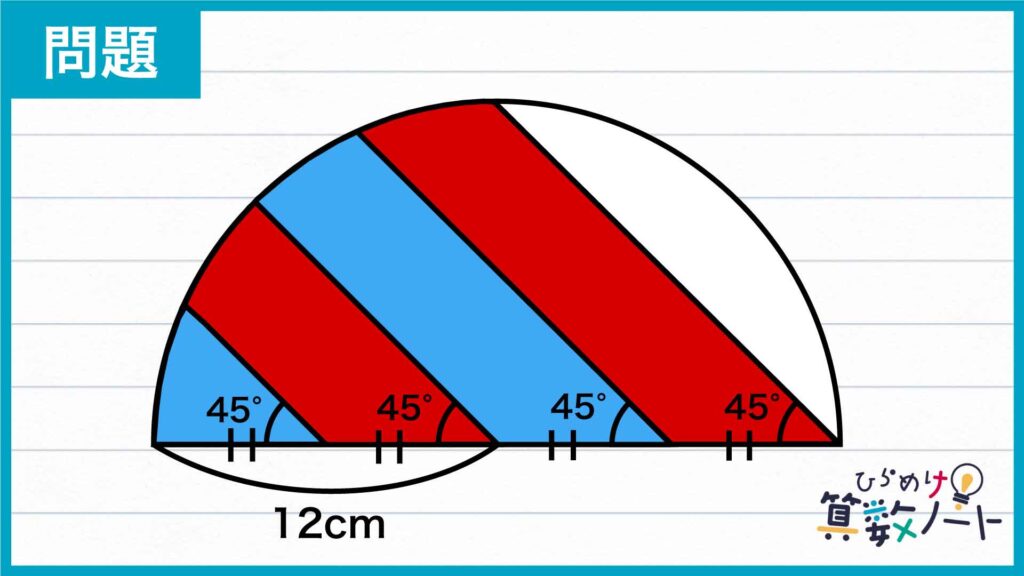
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらです。
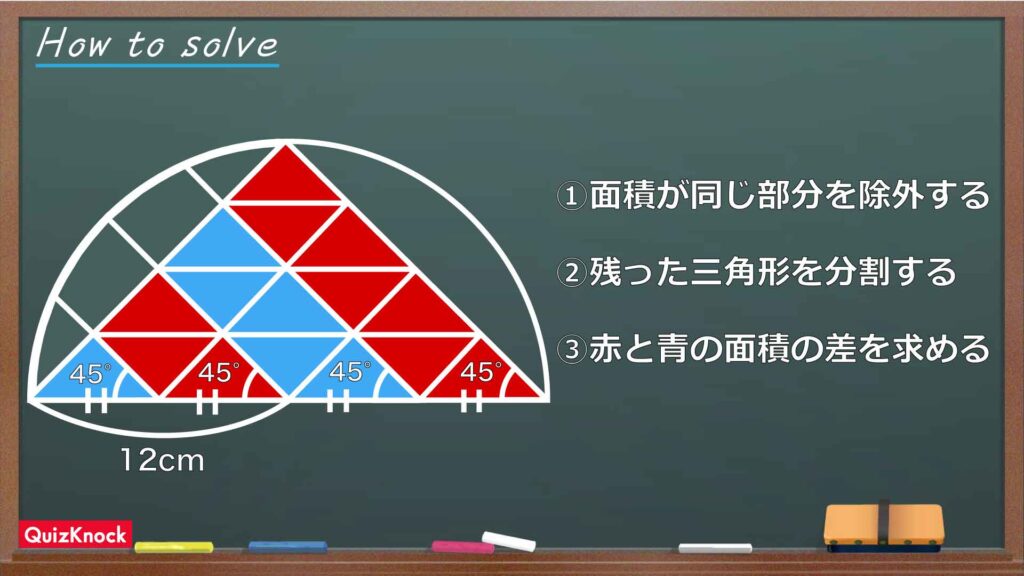
ポイントは、面積の等しい部分に注目し、その部分を取り除いて面積の差を考えることです。これを踏まえて解いていきましょう!
補助線を引く
次の図のように頂点A、B、Cを振り、補助線を引きます。
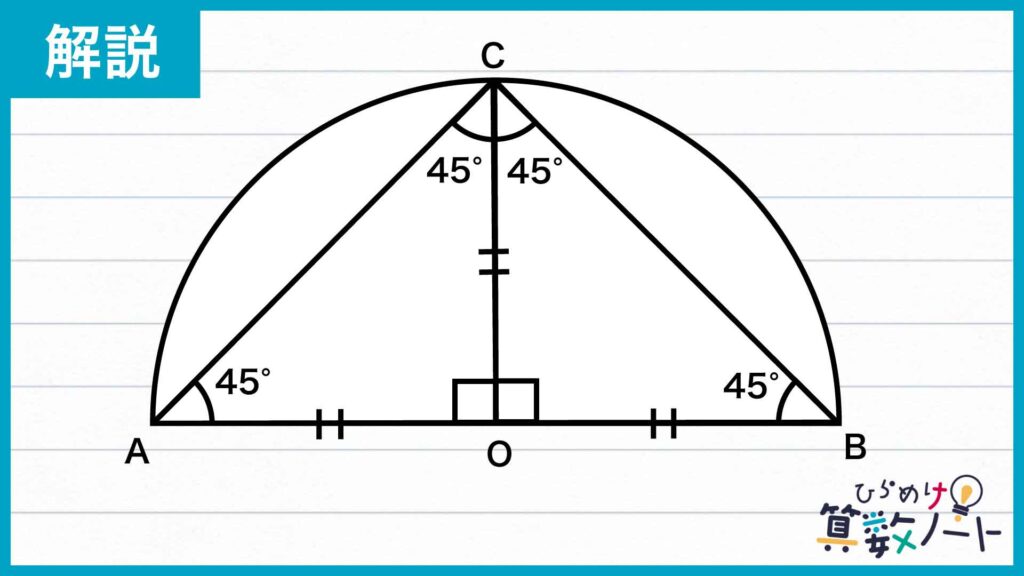
このとき、ABは円の直径なので、その中点であるOは円の中心です。よって、線分OA,OB,OCは円の半径となります。三角形OBCはOB=OCの二等辺三角形なので、角OBC=角OCB=45度であり、角BOC=180-45-45=90度です。さらに、角AOC=180-90=90度であり、三角形OCAはOC=OAの二等辺三角形なので、角OCA=角OAC=45度となります。
よって、三角形ABCと三角形OCAはどちらも直角二等辺三角形になります。
面積が同じ図形を取り除く
次の図のように点Pを振ります。
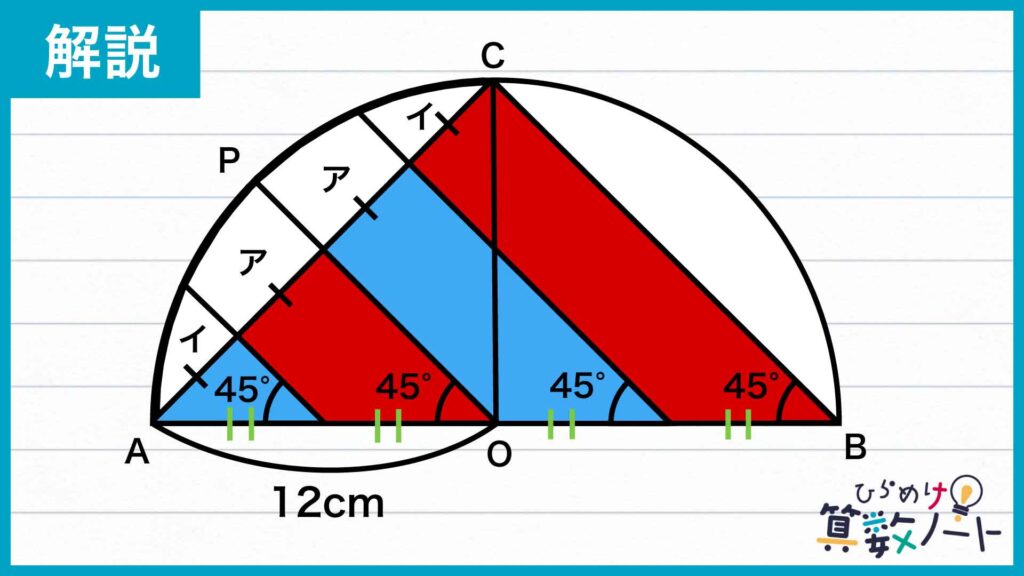
三角形OCAは直角二等辺三角形なので、扇形OCAは中心角が90度の扇型です。そして、この扇型は直線OPに関して線対称です。また、直角三角形ABCにおいて、辺ABの長さを4等分する点から引いた平行線は辺ACの長さも4等分するため、緑の印をつけた線分は長さが等しいです。
このことから、「ア」と名前をつけた2つの図形と、「イ」と名前をつけた2つの図形は、扇形OCAを直線OPで折り返すとちょうど重なり、面積は等しいです。
今回求めるのは、赤と青で色を付けた部分の面積の差であり、両者は「ア」と「イ」を1つずつ含みます。よって、これらの部分を取り除いても面積の差は変わりません。
三角形を分割する
このままでも赤と青の部分の面積を求めることはできますが、もう一工夫することで赤と青それぞれの面積を求めることなく答えを出すことができます。
その一工夫とは、次の図のように、半円の直径と平行な補助線を3本、辺ACと平行な補助線を3本引くことです。
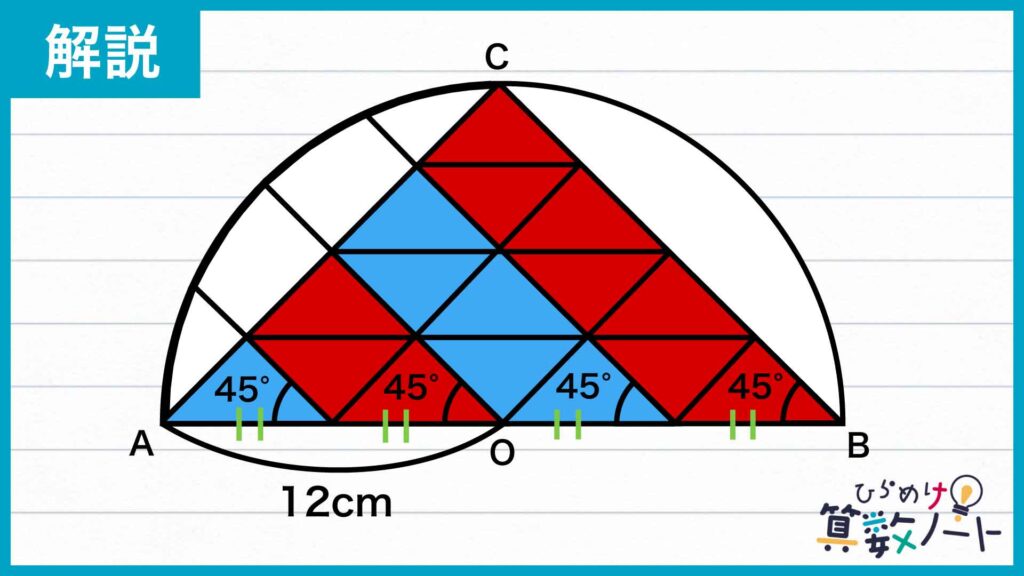
すると、全体の大きな直角二等辺三角形を、同じ形の小さな直角二等辺三角形16個に分けることができます。
赤と青の面積の差を求める
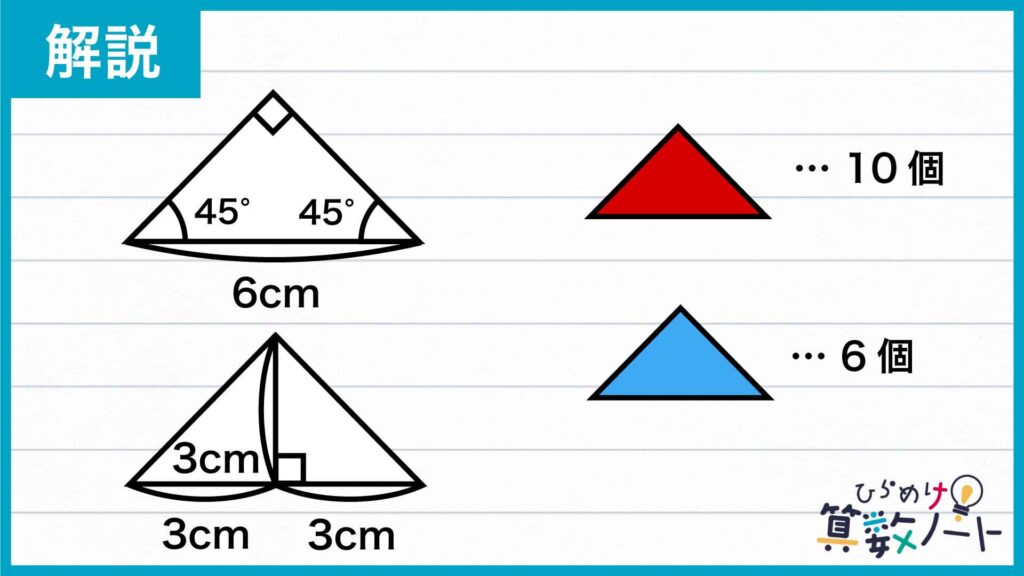
小さな三角形は底辺が6cmの直角二等辺三角形です。頂点から底辺に垂線を降ろすと、同じ長さの辺が3cmの直角二等辺三角形が2つできるので、高さは3cmになります。
赤で色を付けた部分はこの三角形が10個、青で色を付けた部分はこの三角形が6個から成るので、求める面積の差は、6×3÷2×(10-6)=36cm2です。
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)







.jpg)







