【問題はこちら】
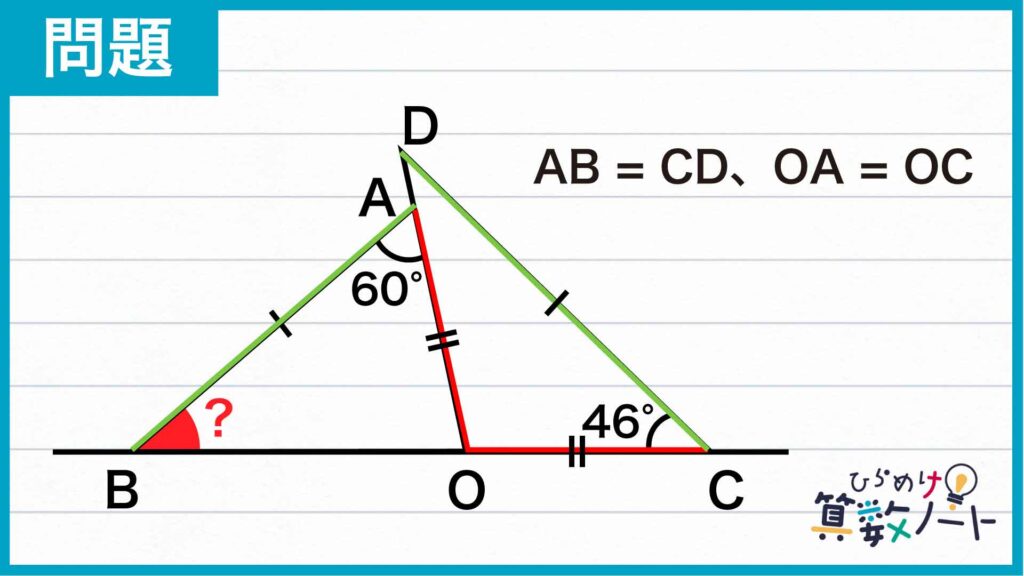
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらです。
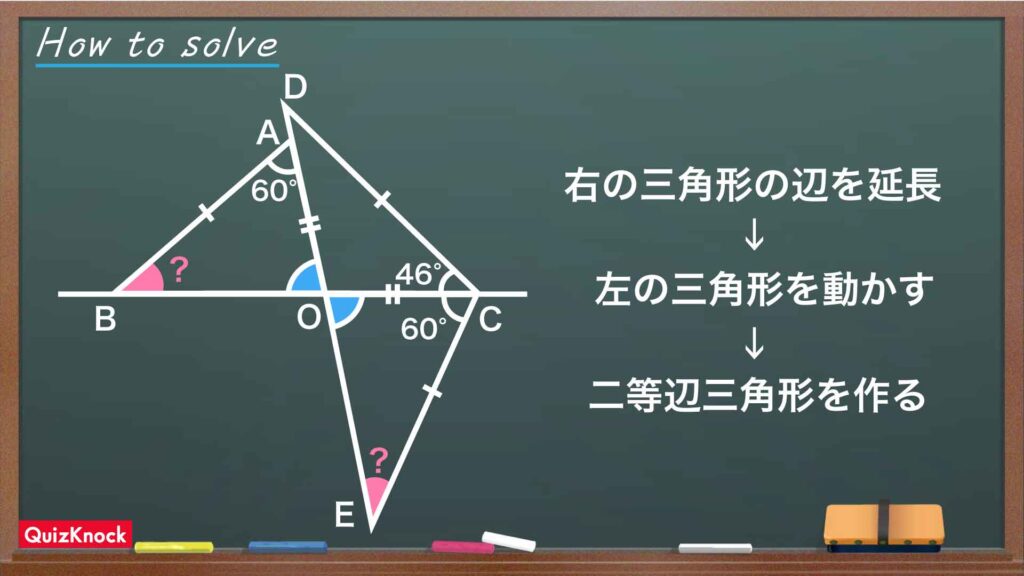
ポイントは、長さの等しい辺に注目し、左の三角形を裏返して移動させることです。これを踏まえて解いていきましょう!
2つの三角形の位置関係に注目する
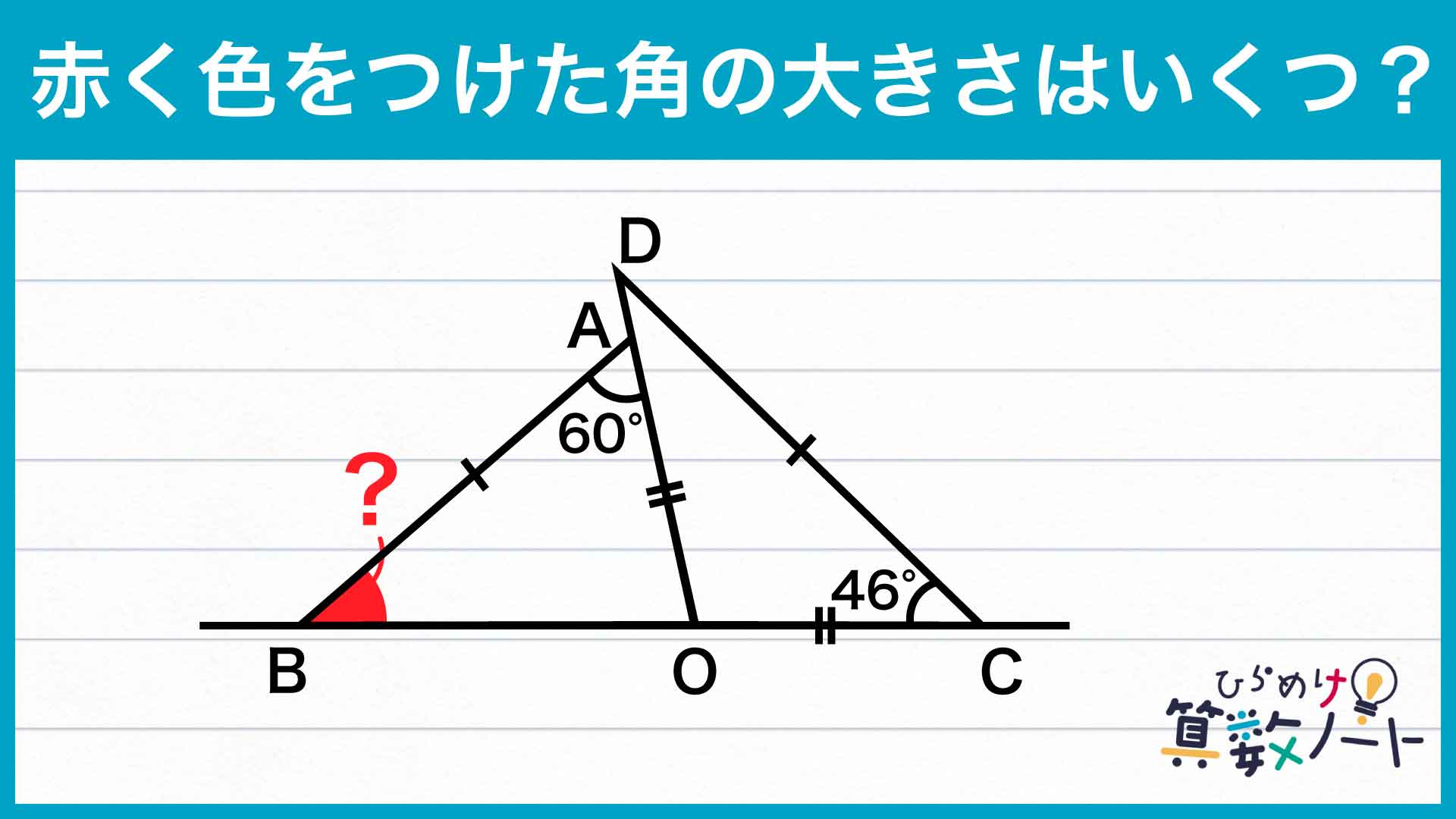
問題の図において、大きさが与えられた2つの角度以外に、角度に関する重要な情報があります。2つの三角形は1つの直線上に位置しており、さらに辺の一部を共有しているため、角BOAと角DOCの大きさの和は180度になります。
数値で与えられていないため気付きにくいですが、角度に関するこの情報は、問題を解く上で大きなヒントになります。
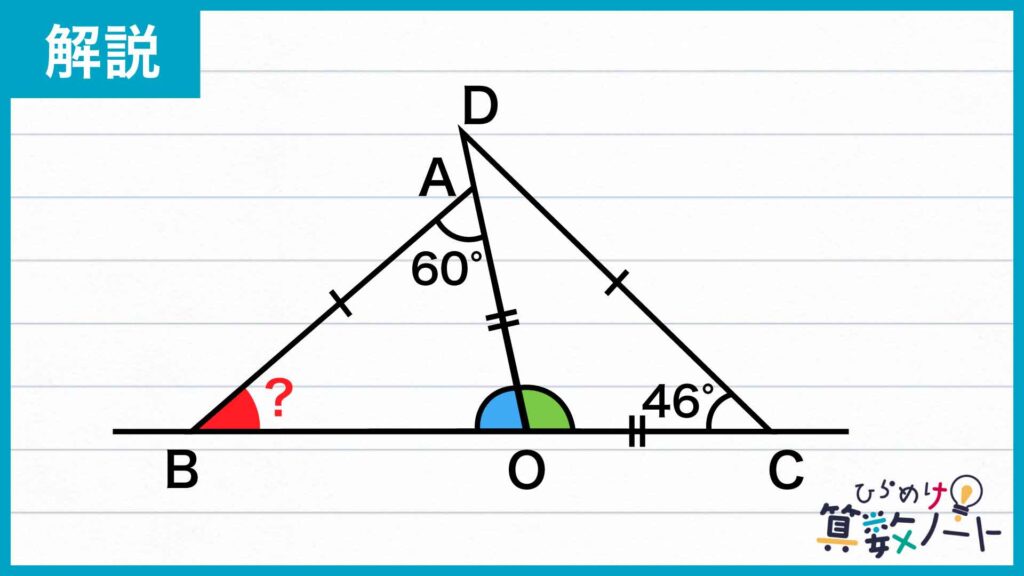
辺DOを延長する
次に、直線DOの延長線上に、OB=OEとなるような点Eをとります。
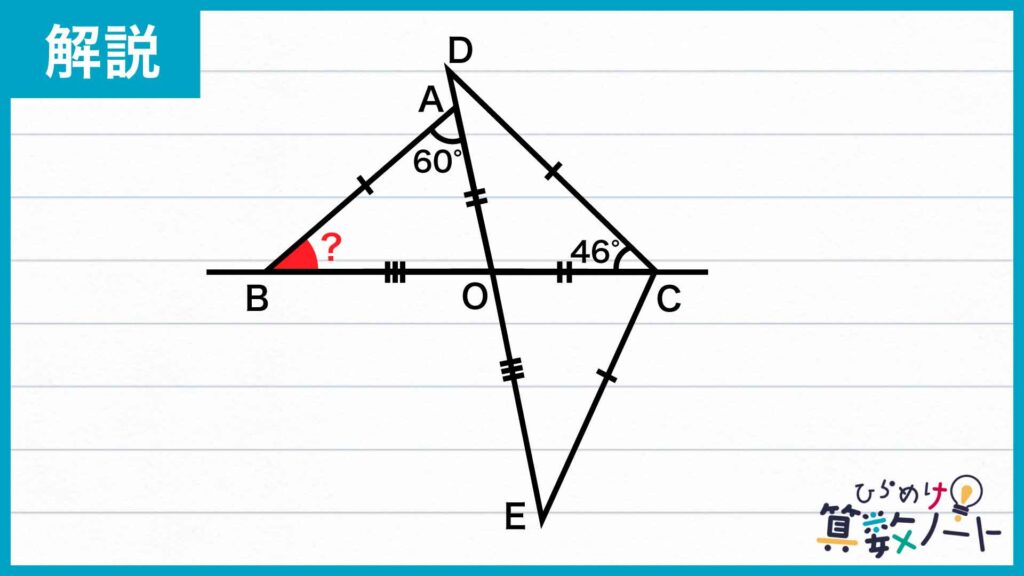
三角形OCEについて考える
こうしてできた三角形OCEについて考えましょう。角EOCは角BOAと対頂角(2本の直線が交わってできる角のうち、互いに向かい合っているもの)の関係にあるため大きさが等しいです。さらに、OE=OB、OC=OAです。よって、三角形OCEと三角形OABは、2つの辺の長さとその間の角の大きさが等しいため合同です。
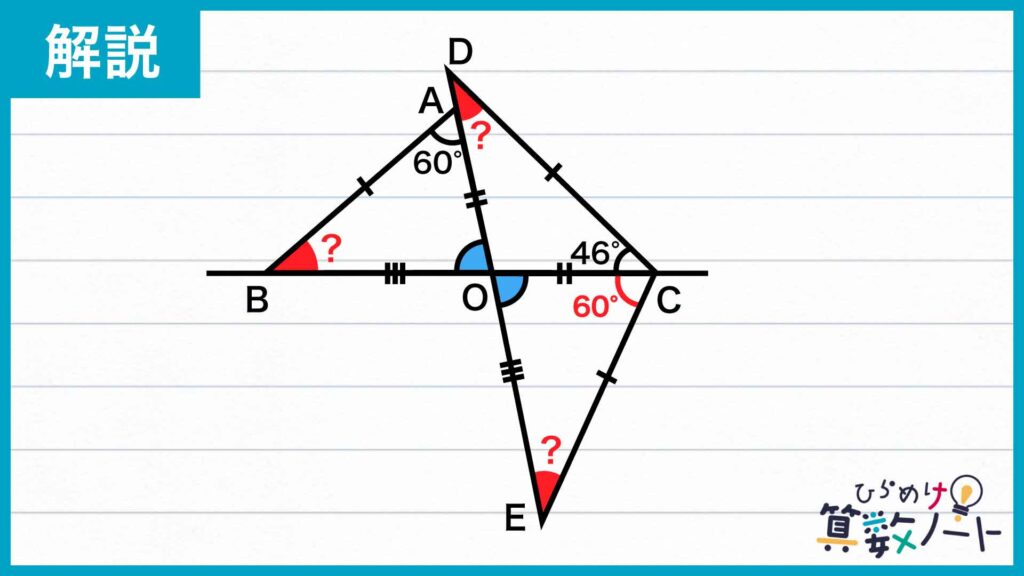
これにより、CE=ABであることがわかります。そして、AB=CDなので、三角形CDEは、CD=CEの二等辺三角形であり、角CED=角CDEとなります。この2角の大きさは求める角度「?」と同じ大きさです。
よって、求める角度の大きさは(180-46-60)÷2=37度です。
答え:37度それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







