小学生でも解ける「図形の面積」の問題にチャレンジ！あなたはひらめけますか？

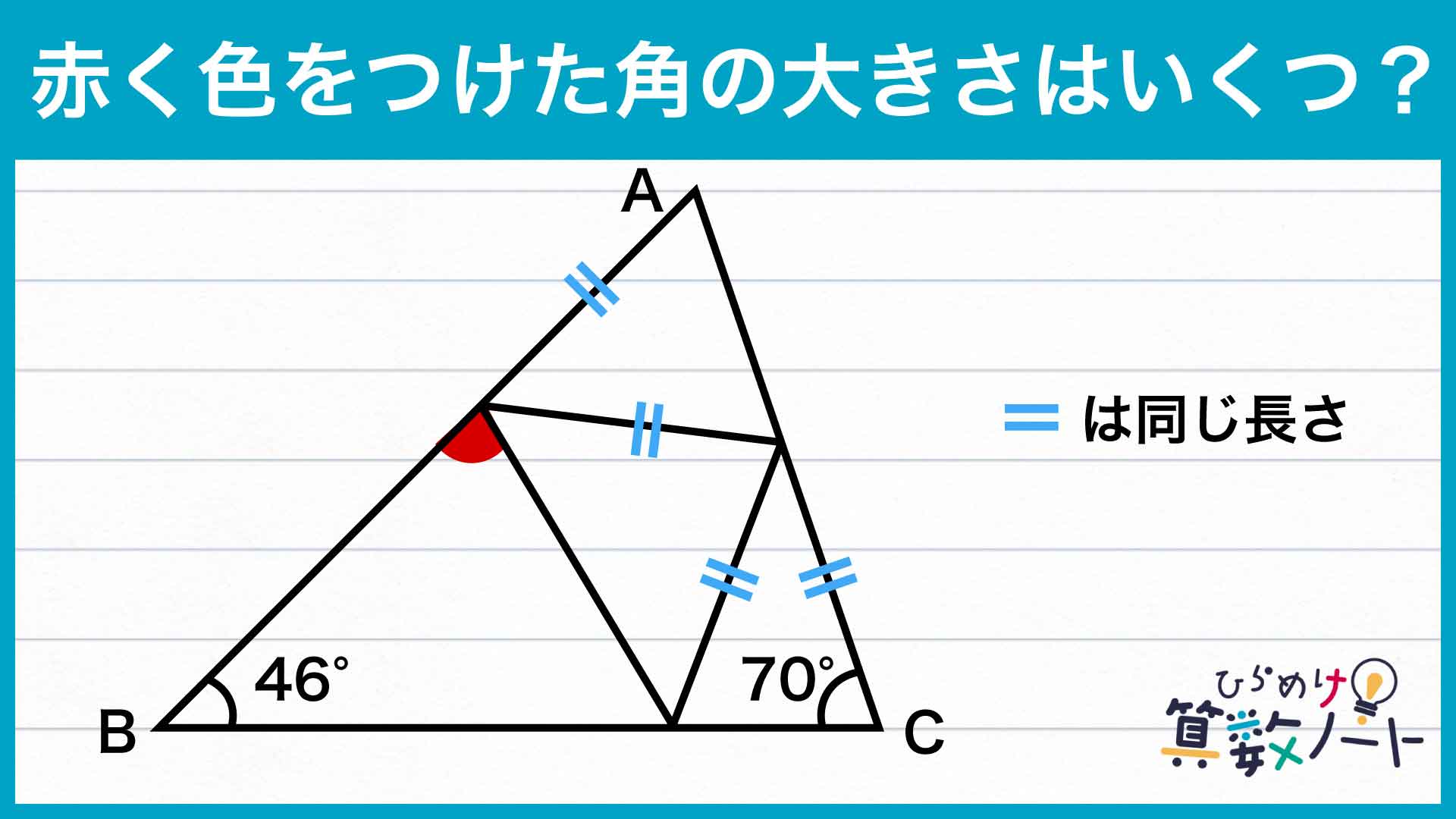
【問題はこちら】

1ページ目：自力で解きたい方はこちらへ！以下は問題の解説です

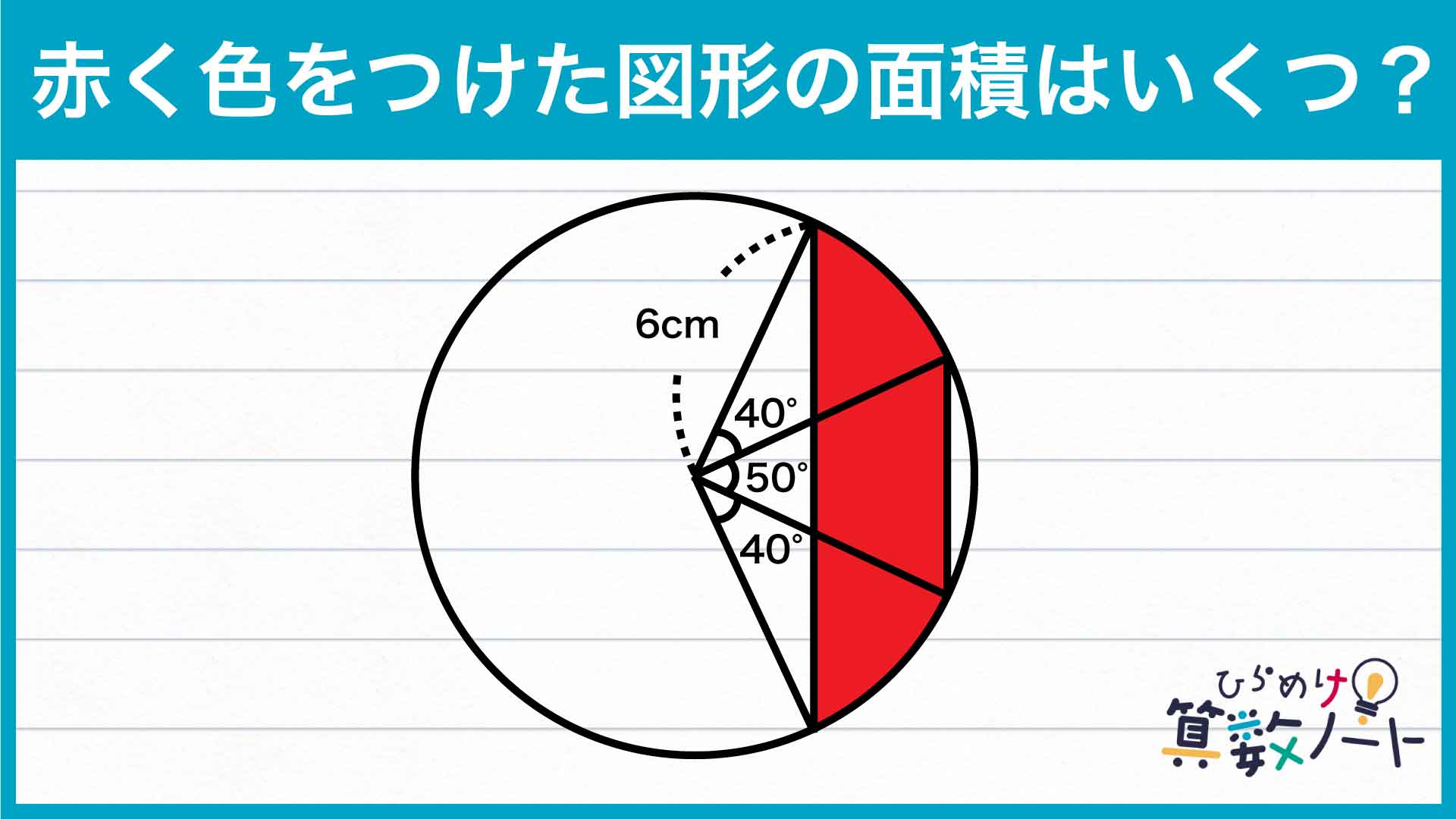
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題の解き方をまとめた図がこちらになります。

ポイントは、円の中心から補助線を引いて、面積が同じ図形に変形することです。これを踏まえて解いていきましょう！

点Oから角BOCの二等分線を引く

下の図のように、円の中心をOとし、点A、点B、点C、点Dをとります。点Oから角BOCの二等分線を引き、線分ADと線分BCとの交点をそれぞれ点E、点Fとします。

このとき、赤い色を塗った図形は角BOCの二等分線に関して線対称なので、角BOCの二等分線より上の部分の面積を求めて最後に2倍すると、最終的な答えが得られます。

ここで、三角形OAEと三角形BOFに注目します。辺OAと辺BOはともに円の半径なので長さが等しく、また対称性より、角AEO=角OFB=90度です。さらに、角BOC=50度なので、角BOFの大きさはその半分の25度であり、角OAE=180-90-65=25度、角EOA=25+40=65度、角FBO=180-90-25=65度です。

以上より、OA=BO、角OAE=角BOF、角EOA=角FBOであり、三角形OAEと三角形BOFは、1つの辺の長さと、その両端の角の大きさがそれぞれ等しいため合同です。

三角形AOGと四角形BGEFに注目する

次に、下の図のように、線分OBと線分ADの交点を点Gとします。

ここで、三角形AOGと四角形BGEFに注目します。三角形AOGと四角形BGEFの面積はそれぞれ、三角形OAEと三角形BOFの面積から三角形OEGの面積を引いたものです。三角形OAEと三角形BOFは合同なので面積が等しく、これらの三角形から三角形OEGを除いた三角形AOGと四角形BGEFの面積も等しくなります。

赤い図形を変形して面積を求める

面積を求めたい赤い図形のうち、四角形BGEFは三角形AOGと面積が等しいため、下の図のように赤い図形を変形しても面積は変わりません。

こうして変形した図形は、半径が6cm、中心角が40度の扇形なので、その面積は6×6×π×(40/360)=4πcm²です。これは求めたい面積の半分なので、答えはこれを2倍した8πcm²になります。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】