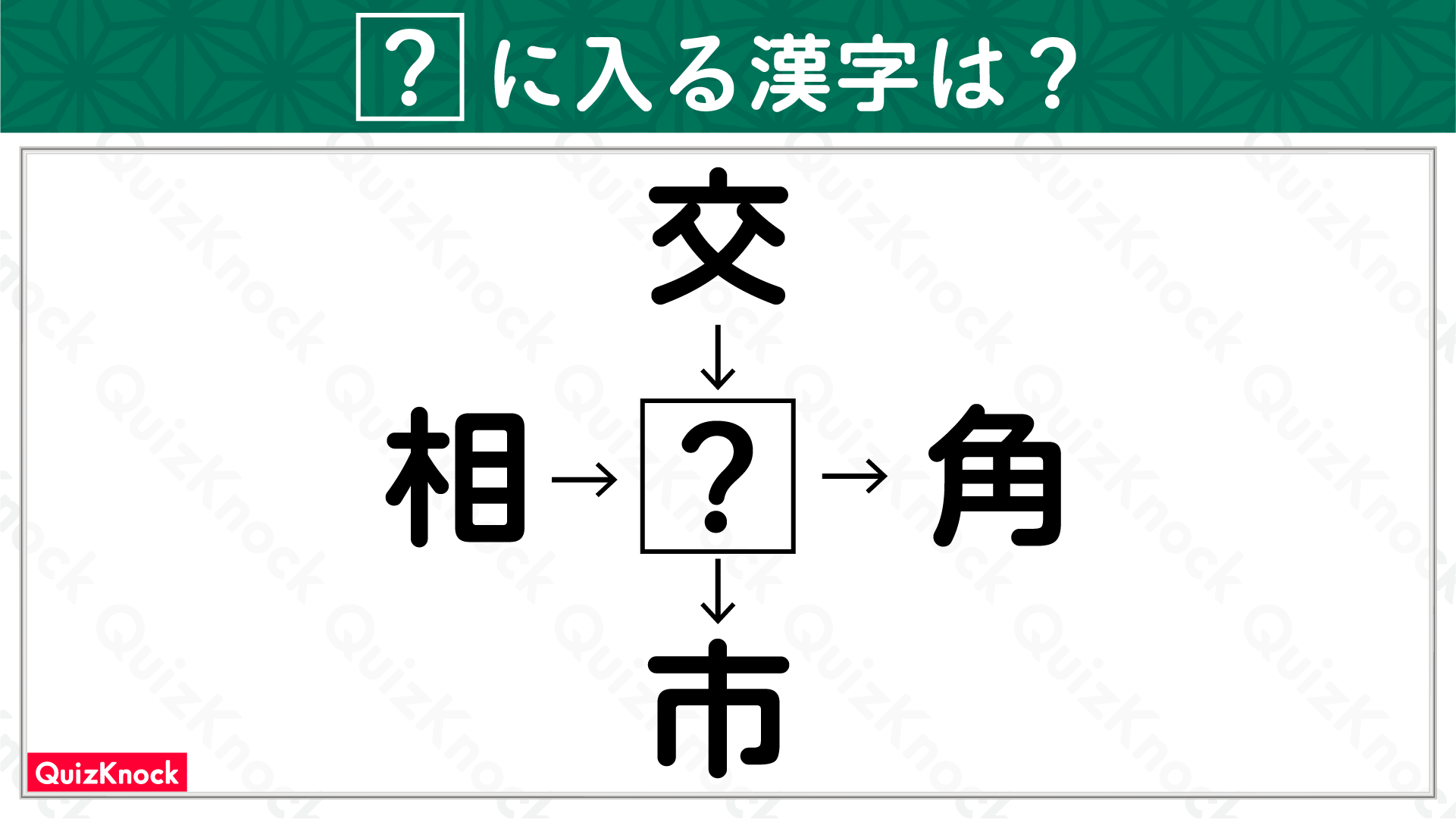
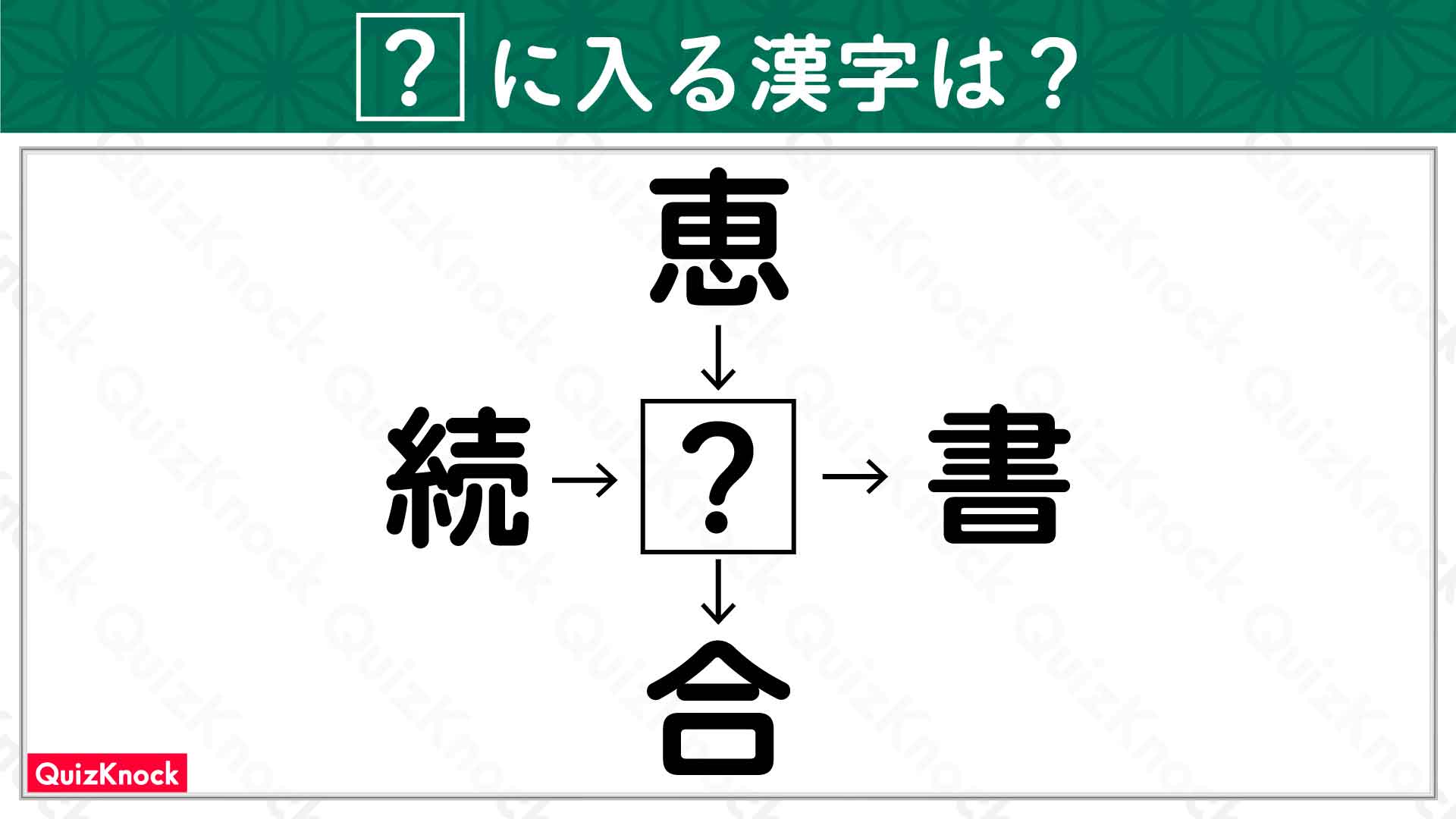
問題はこちら
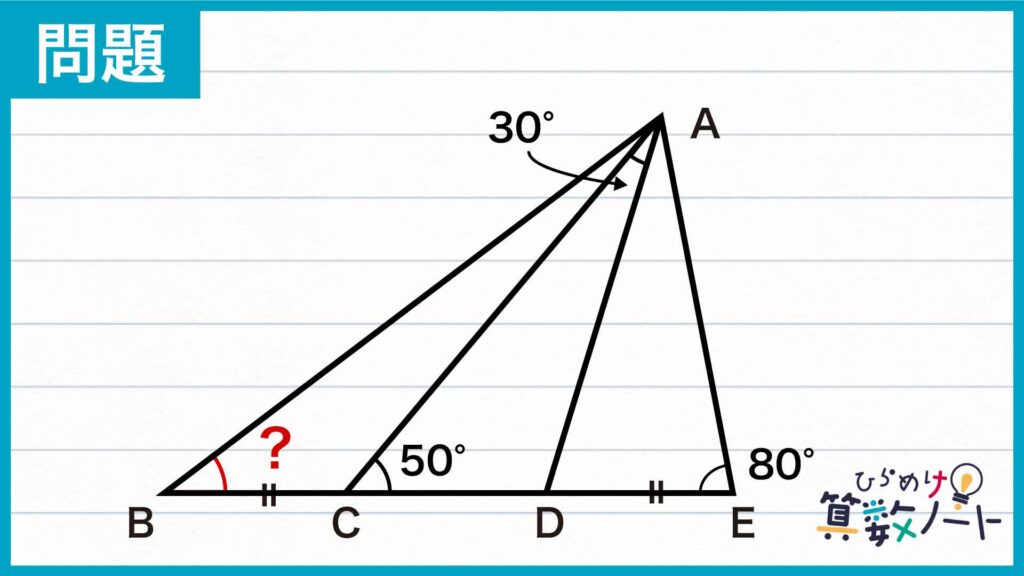
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
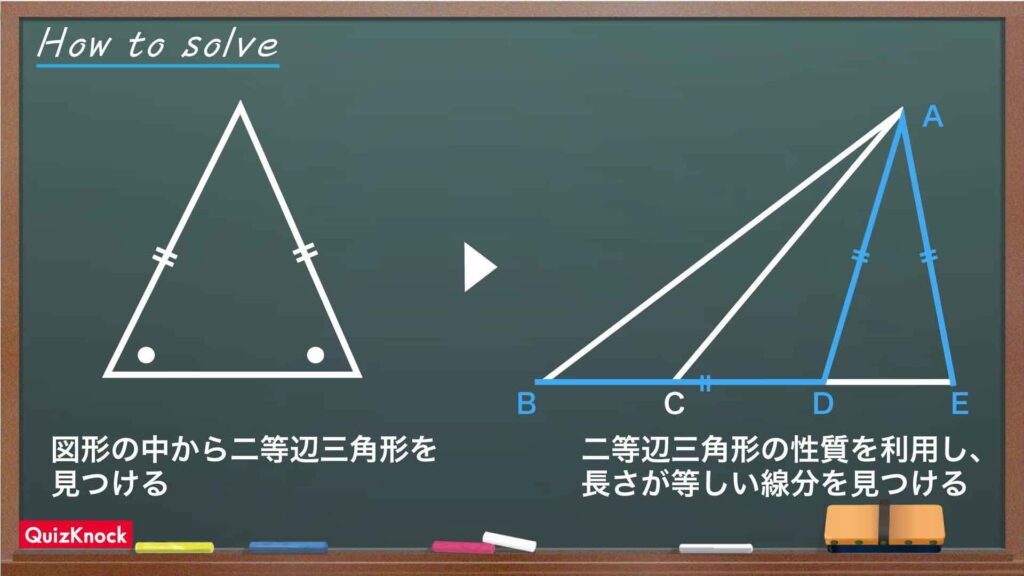
整理すると、
- 図形の中から二等辺三角形を見つける
- 長さが等しい線分を見つけ、二等辺三角形の性質を利用する
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
図形の中から二等辺三角形を見つける
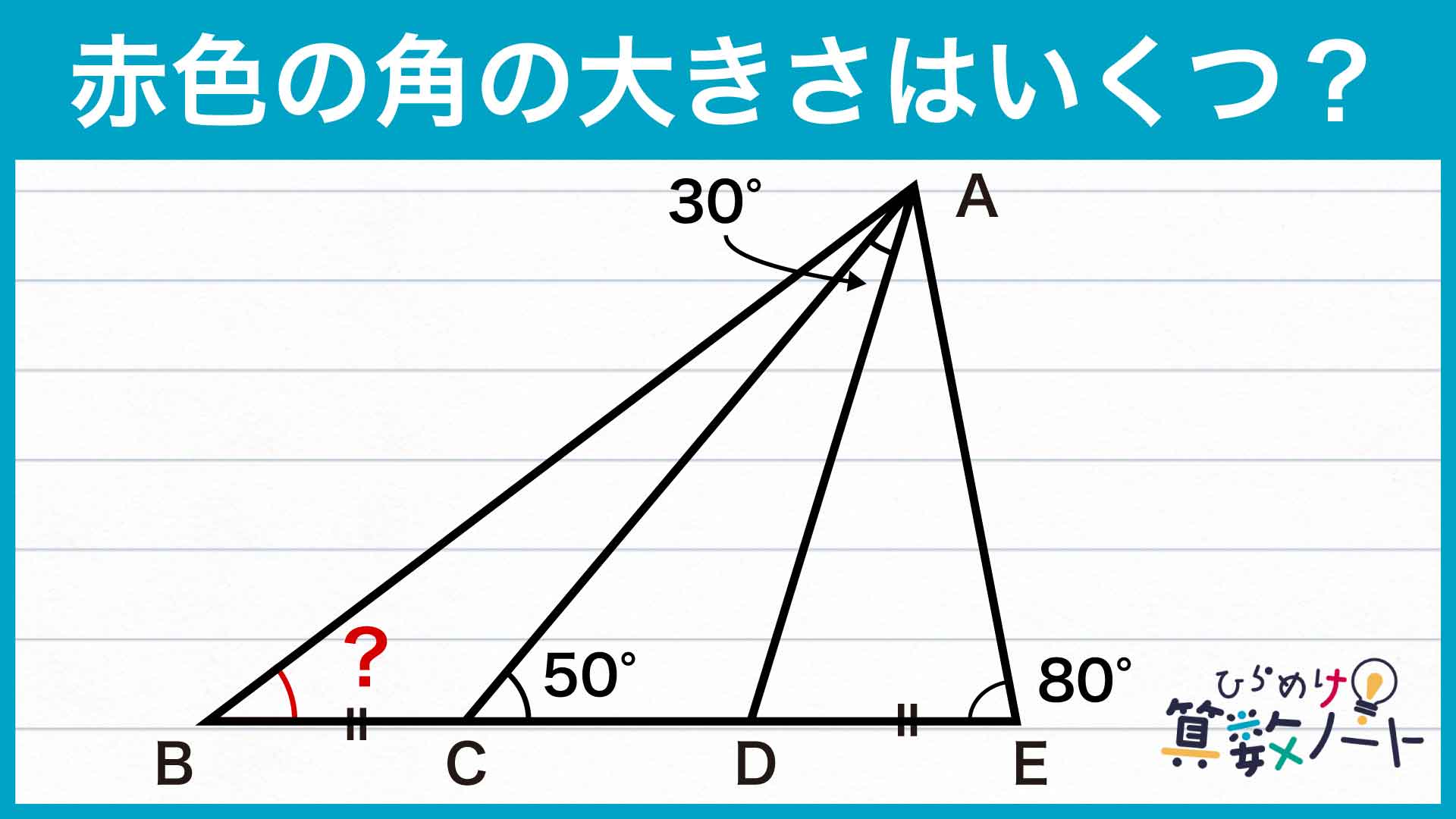
問題の条件から、角CADの大きさが30度、角ACDの大きさが50度であるので、角ADC=180-(30+50)=100度となり、角ADEの大きさが180-100=80度であることがわかります。よって、角ADE=角AED=80度なので、三角形ADEは二等辺三角形になります。
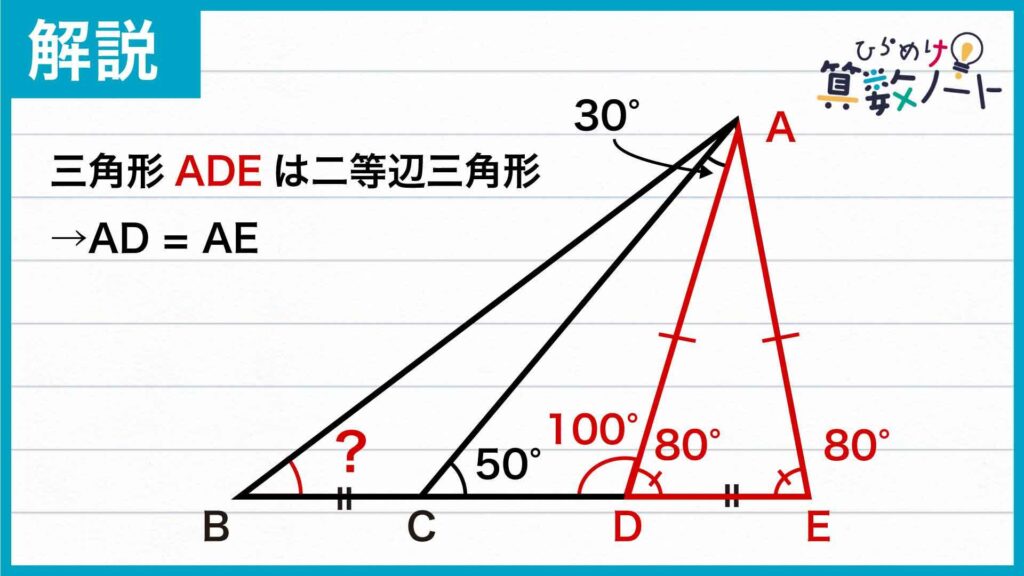
また、三角形ACEに注目すると、角ACEの大きさが50度、角AECの大きさが80度であることから、角CAE=180-(50+80)=50度になります。よって、角ACE=角CAE=50度なので、三角形ACEも二等辺三角形になります。
したがって、三角形ADEが二等辺三角形であることからAD=AE、三角形ACEが二等辺三角形であることからAE=CEであるので、AD=AE=CEであることがわかります。
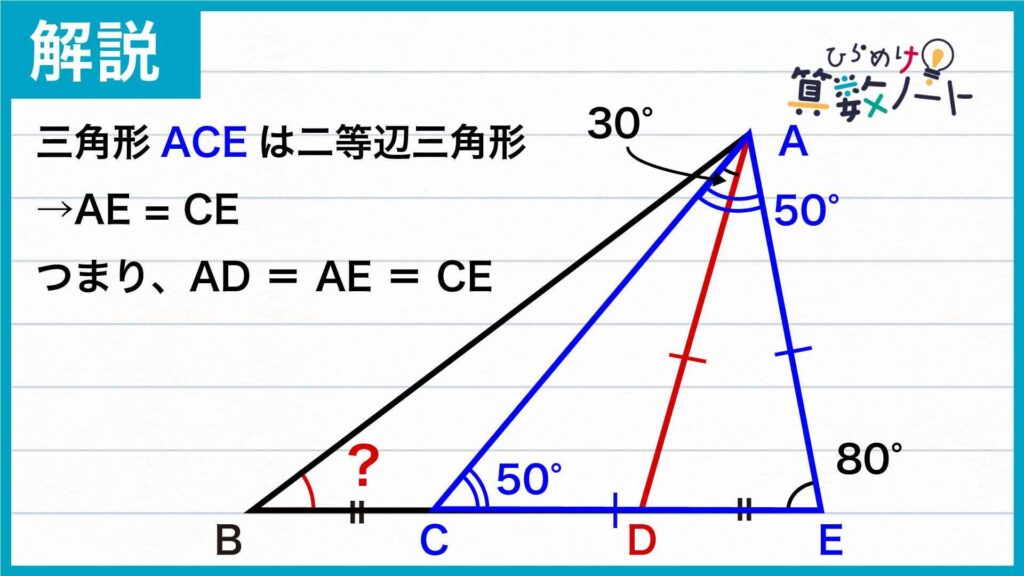
二等辺三角形の性質を利用し長さが等しい線分を見つける
問題の条件であるBC=DEを用いるため、BDの長さをBD=BC+CDのように分割します。すると、BC=DEであることから、BD=BC+CD=DE+CD=CEがわかります。
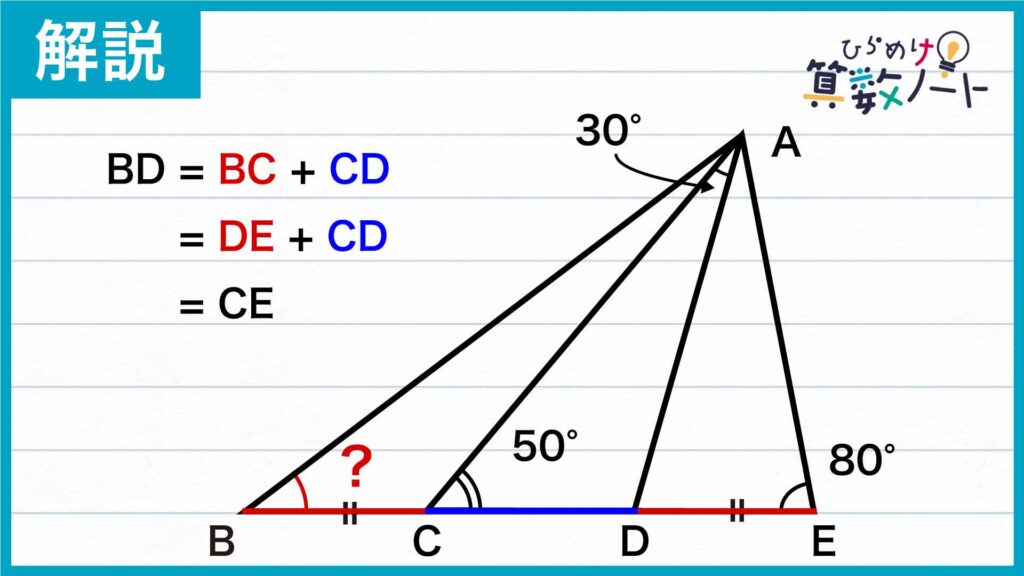
よって、BD=CEと先ほどのAD=AE=CEを用いることで、AD=BDであることがわかります。したがって、三角形ABDは二等辺三角形です。二等辺三角形の性質から、角DAB=角DBAであり、角ADB=100度であることを用いて、角DAB=角DBA=(180-100)÷2=40度であることがわかります。したがって、求める角度は40度になります。
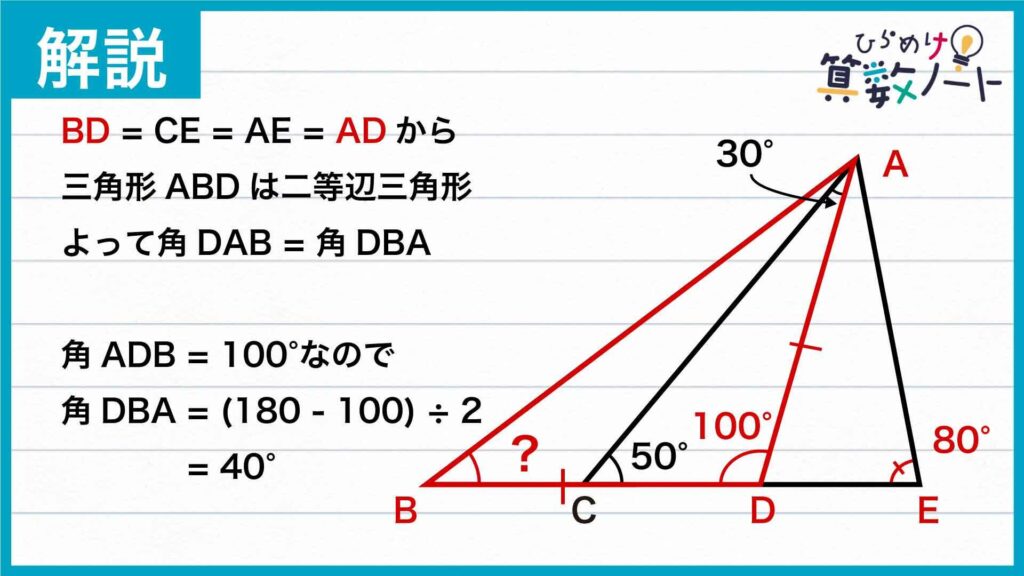
答え:40度
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】