中学受験レベル！「正方形の面積」の問題、あなたは解ける？

【問題はこちら】

1ページ目：自力で解きたい方はこちらへ！以下は問題の解説です

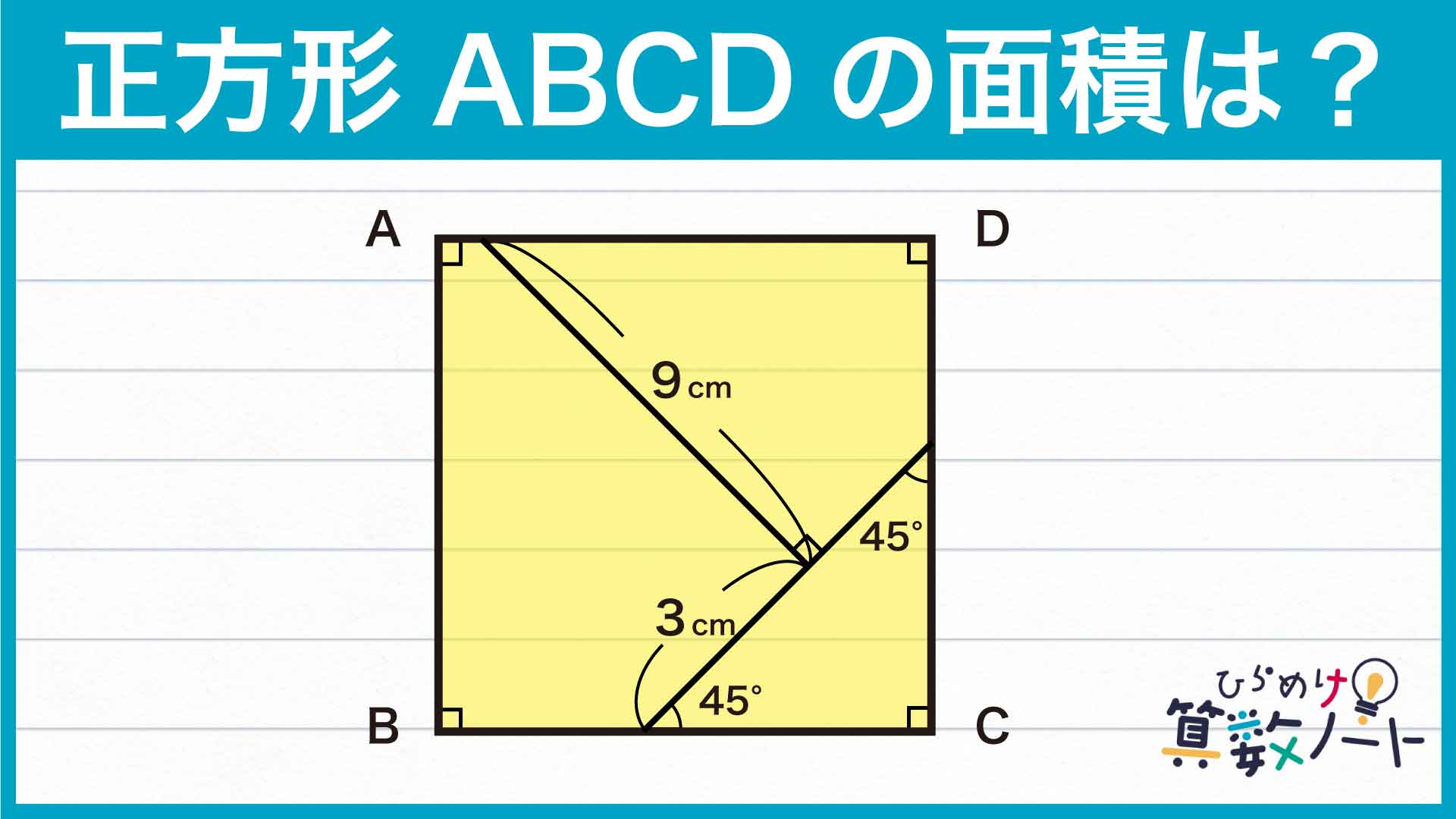
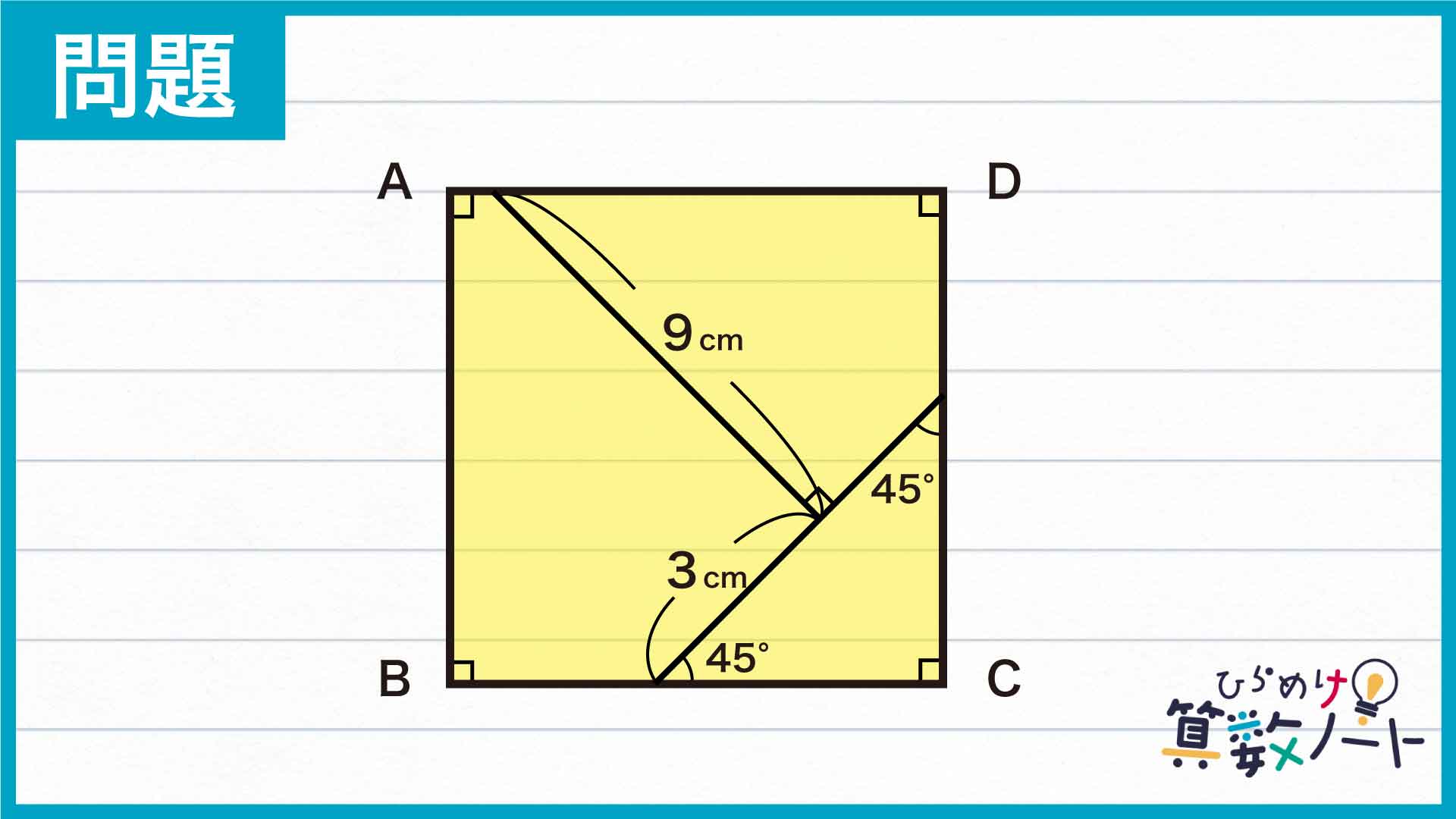
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

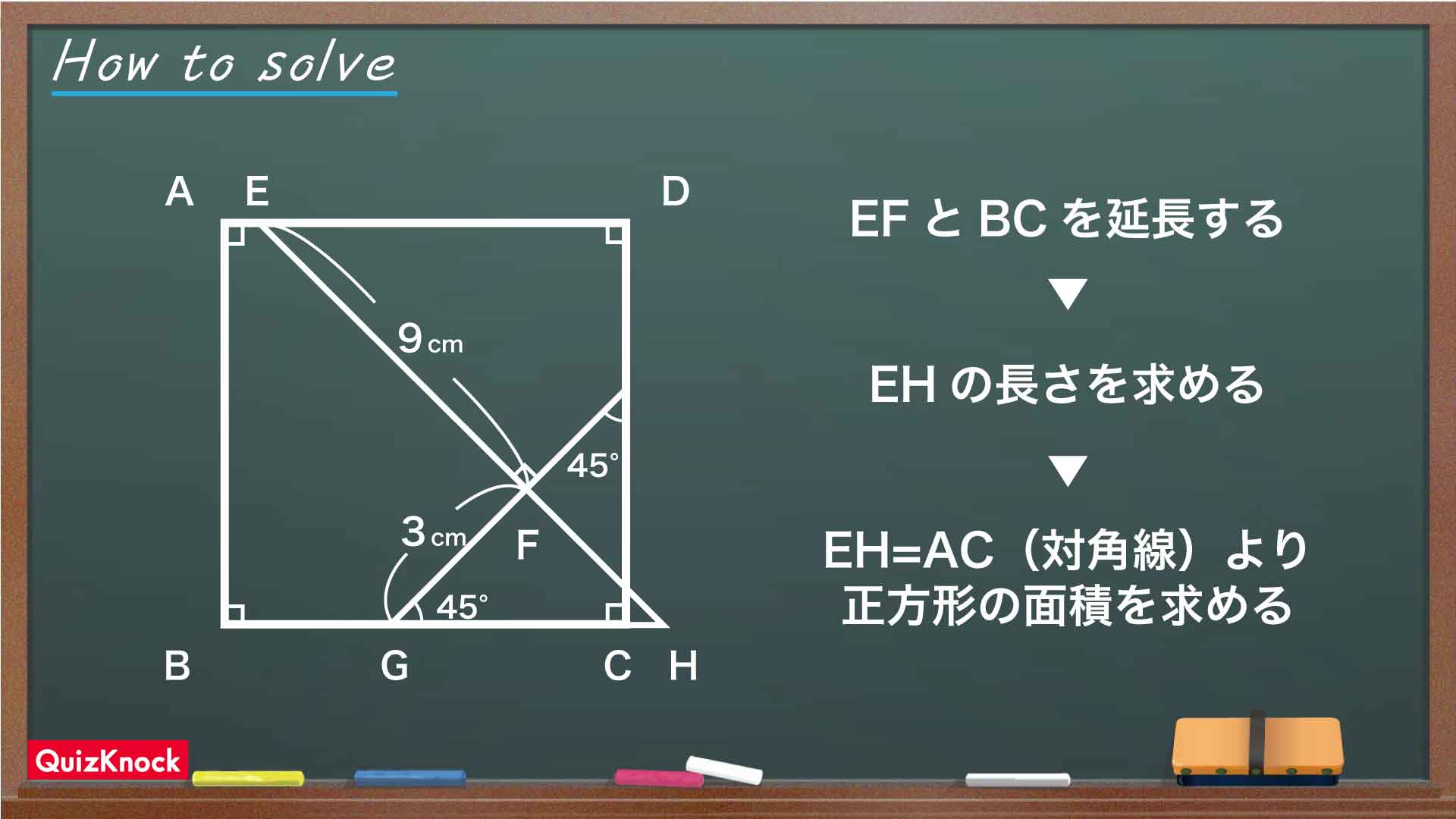
今回の問題の解き方をまとめた図がこちらになります。

ポイントは、45度という角度に注目して線分を延長し、直角二等辺三角形を作ることです。これを踏まえて解いていきましょう！

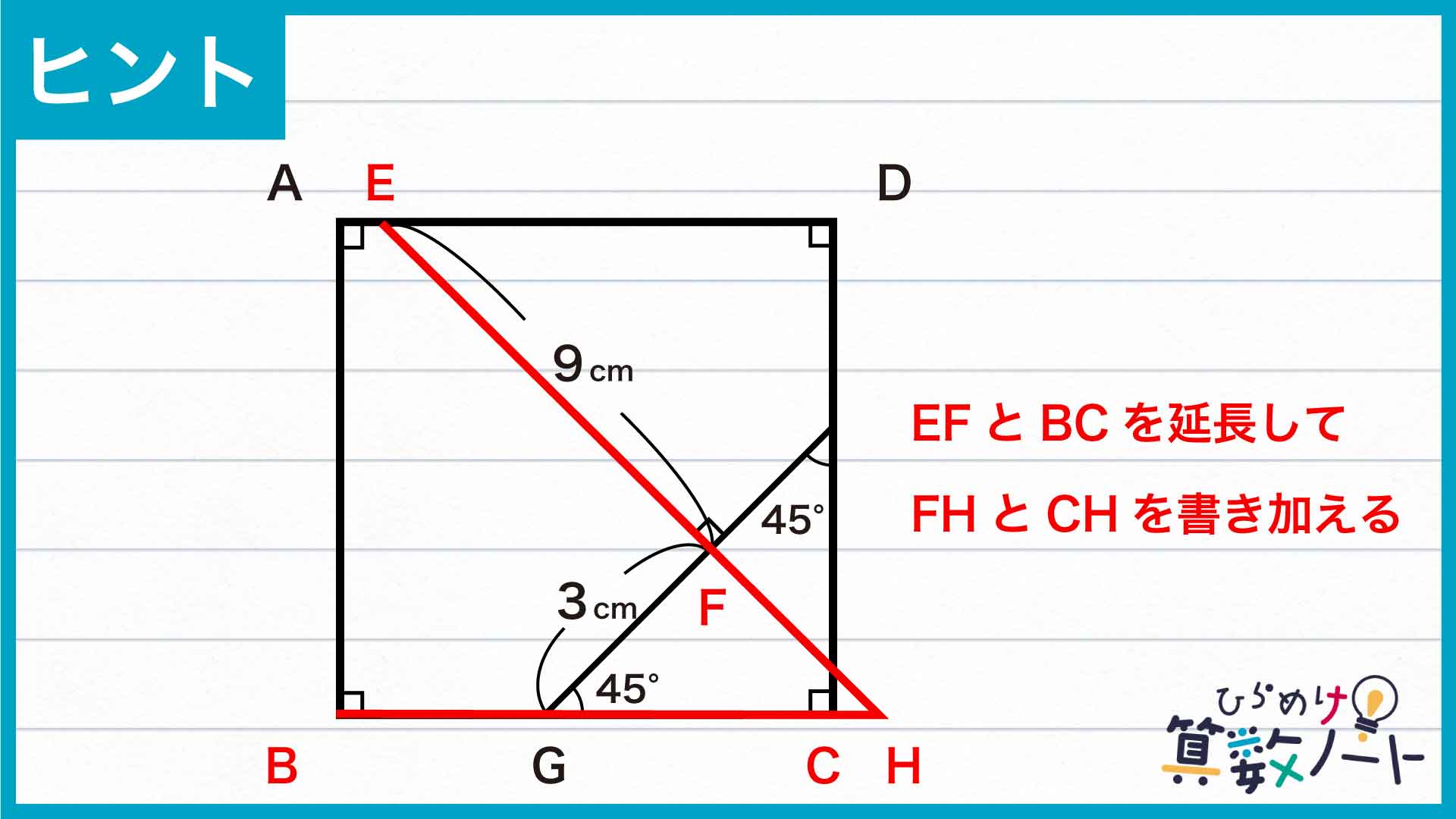
線分を延長する

下の図のように、点E、点F、点Gを振り、線分EFと線分BCの延長線が交わる点をHとします。

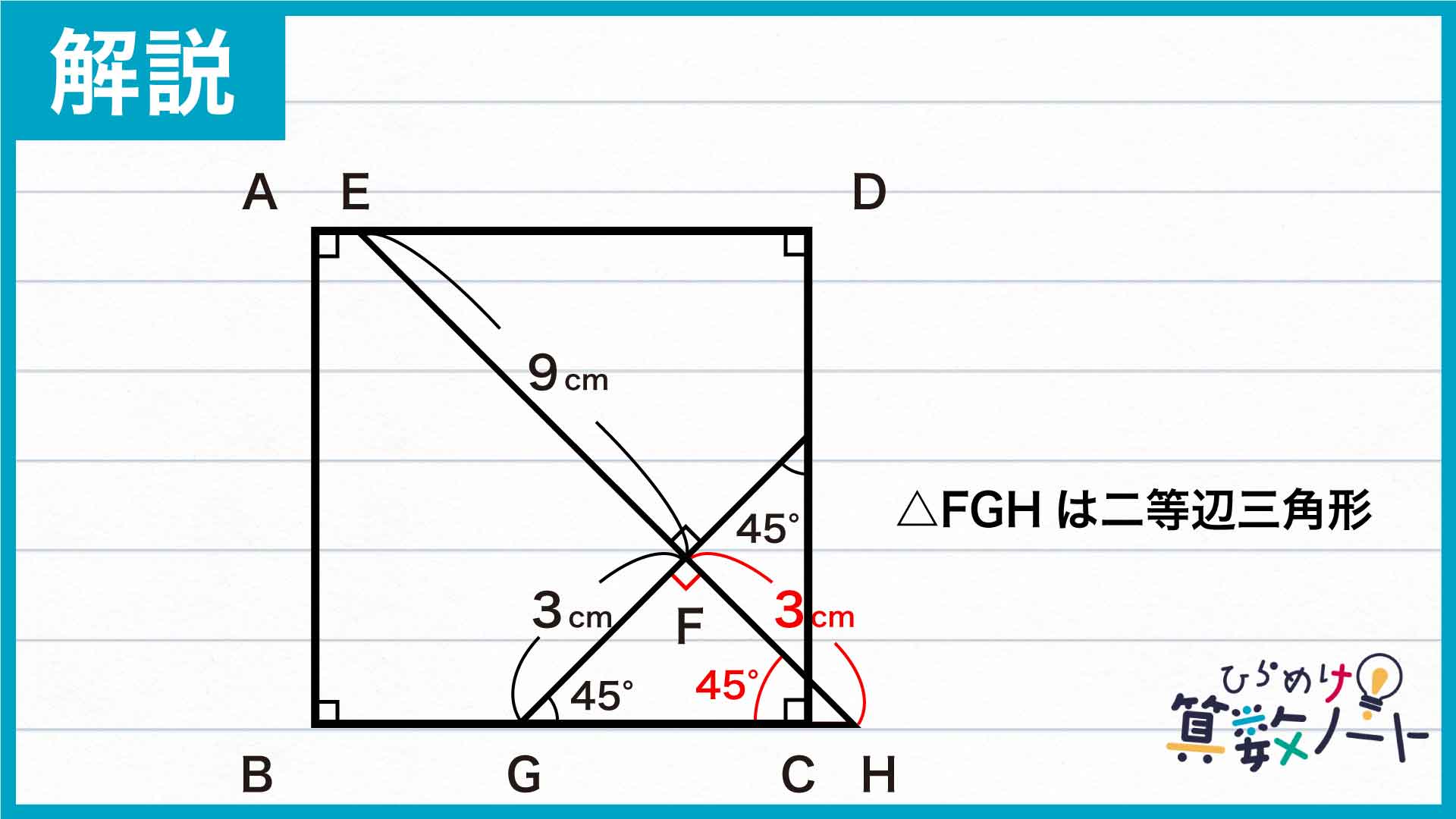
このとき、角FGHは45度、角HFGは90度なので、角GHFは45度となり、三角形FGHは直角二等辺三角形であることがわかります。よって、FG=FHであり、FH=3cmです。さらに、EH=EF+FHなので、線分EHの長さは9+3=12cmです。

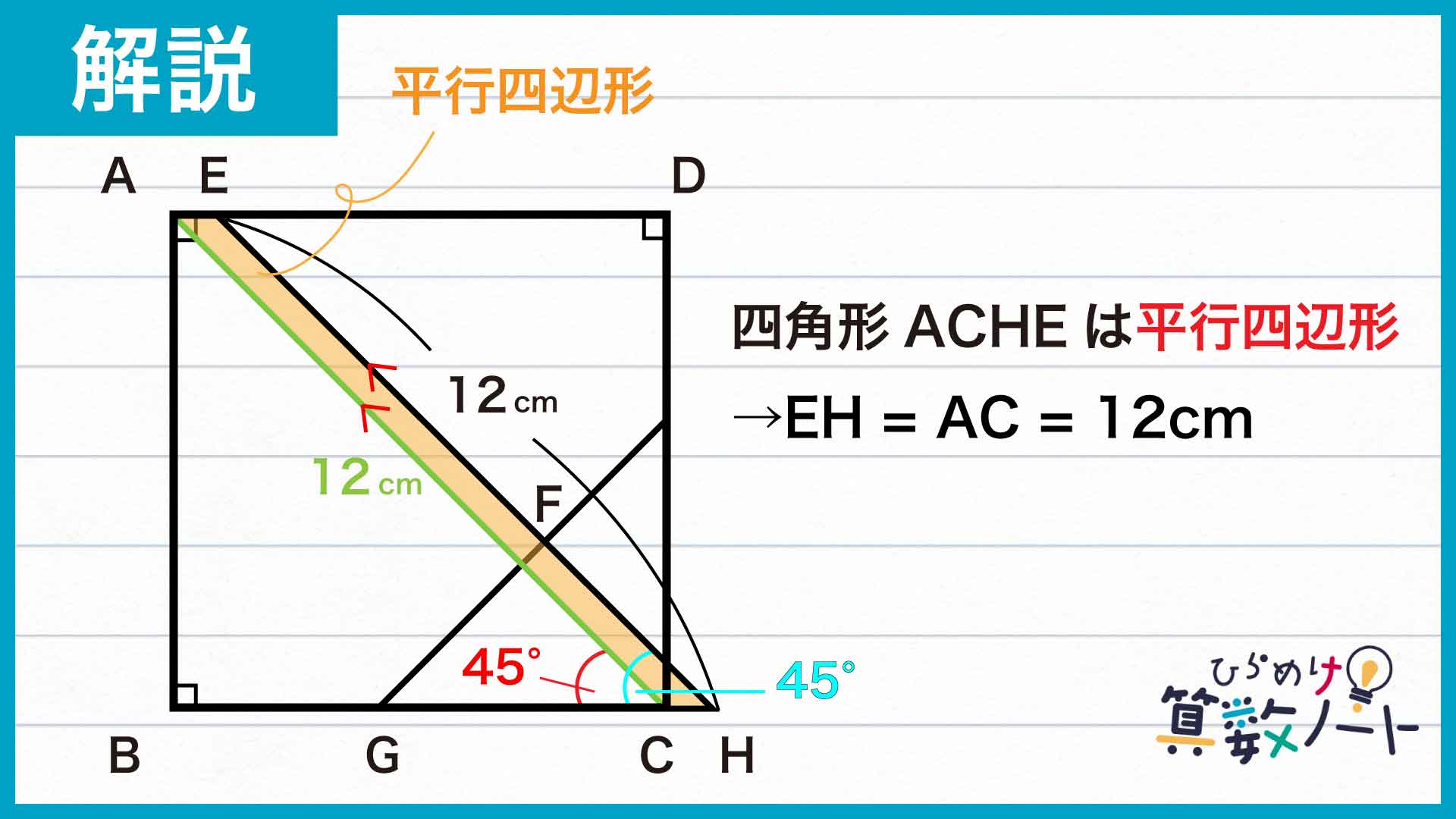
線分ACの長さを求める

線分ACを引き、四角形ACHEに注目します。線分ACは正方形ABCDの対角線なので、角BCAは45度です。角CHEも45度であり、ACとEHは平行であることがわかります。また、点Hは辺BCの延長線上にあるので、AEとCHも平行です。よって、四角形ACHEは平行四辺形であり、線分ACの長さは、向かい合う線分EHの長さと等しく、12cmです。

よって、正方形ABCDは対角線の長さが12cmなので、面積は12×12÷2=72cm²です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

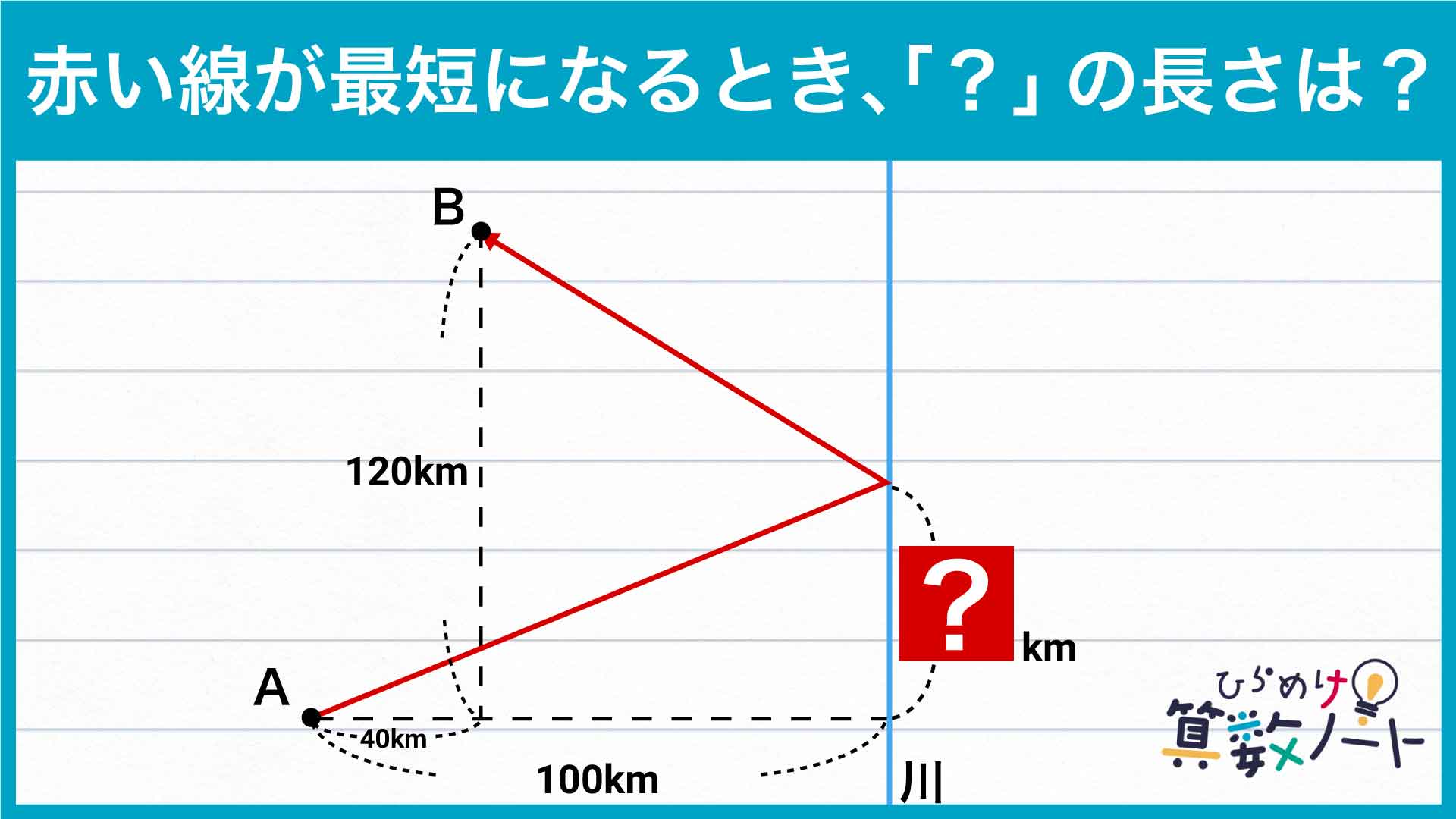
【前回の算数ノートはこちら】

【あわせて読みたい】