ヒント
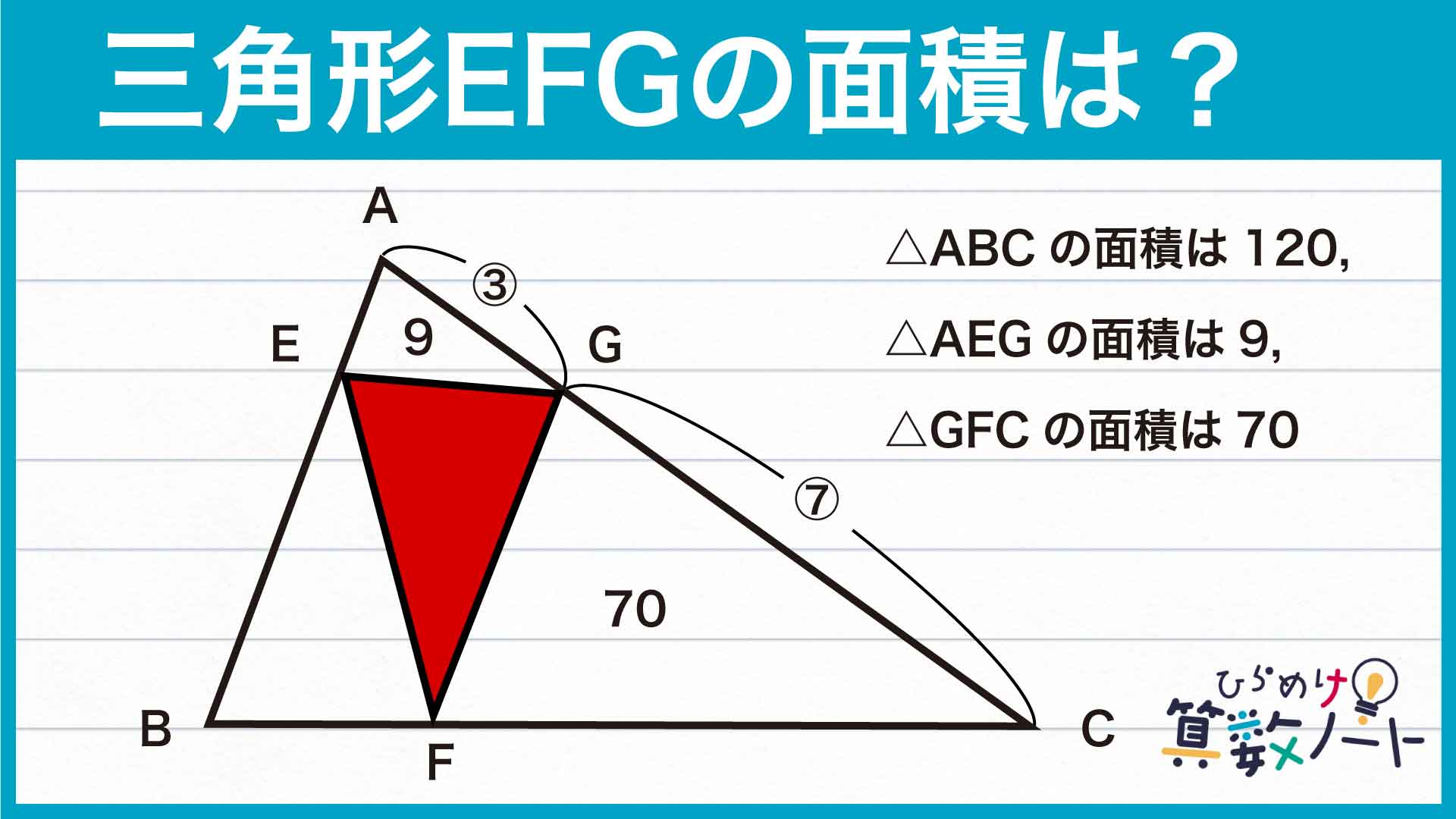
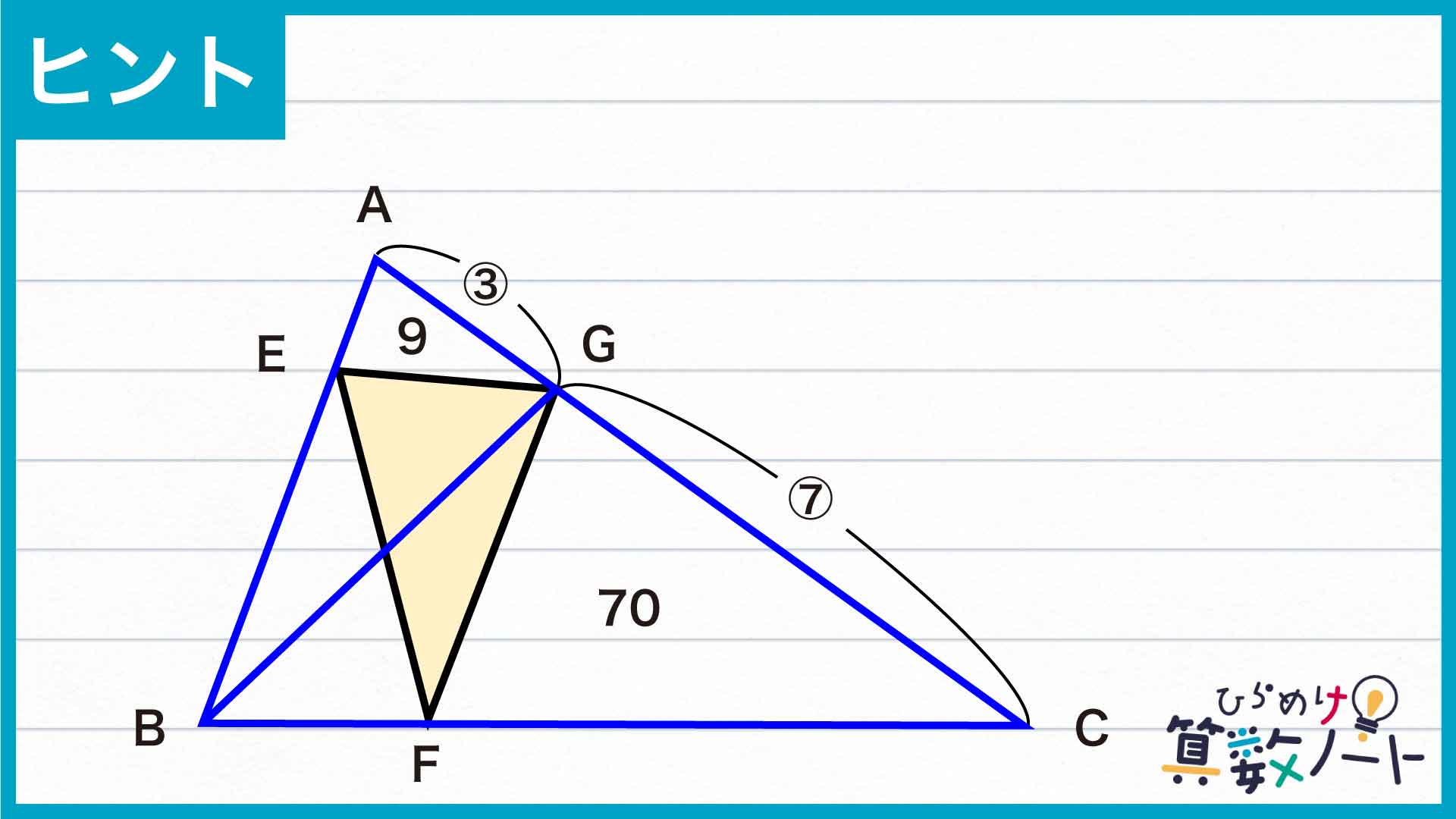
三角形の面積について考える際には、「高さが等しい三角形の面積比は底辺の長さの比に等しくなる」という考え方が便利です。今回はAGとGCの長さの比がわかっているので、三角形ABCを下の図のように分割してみましょう。
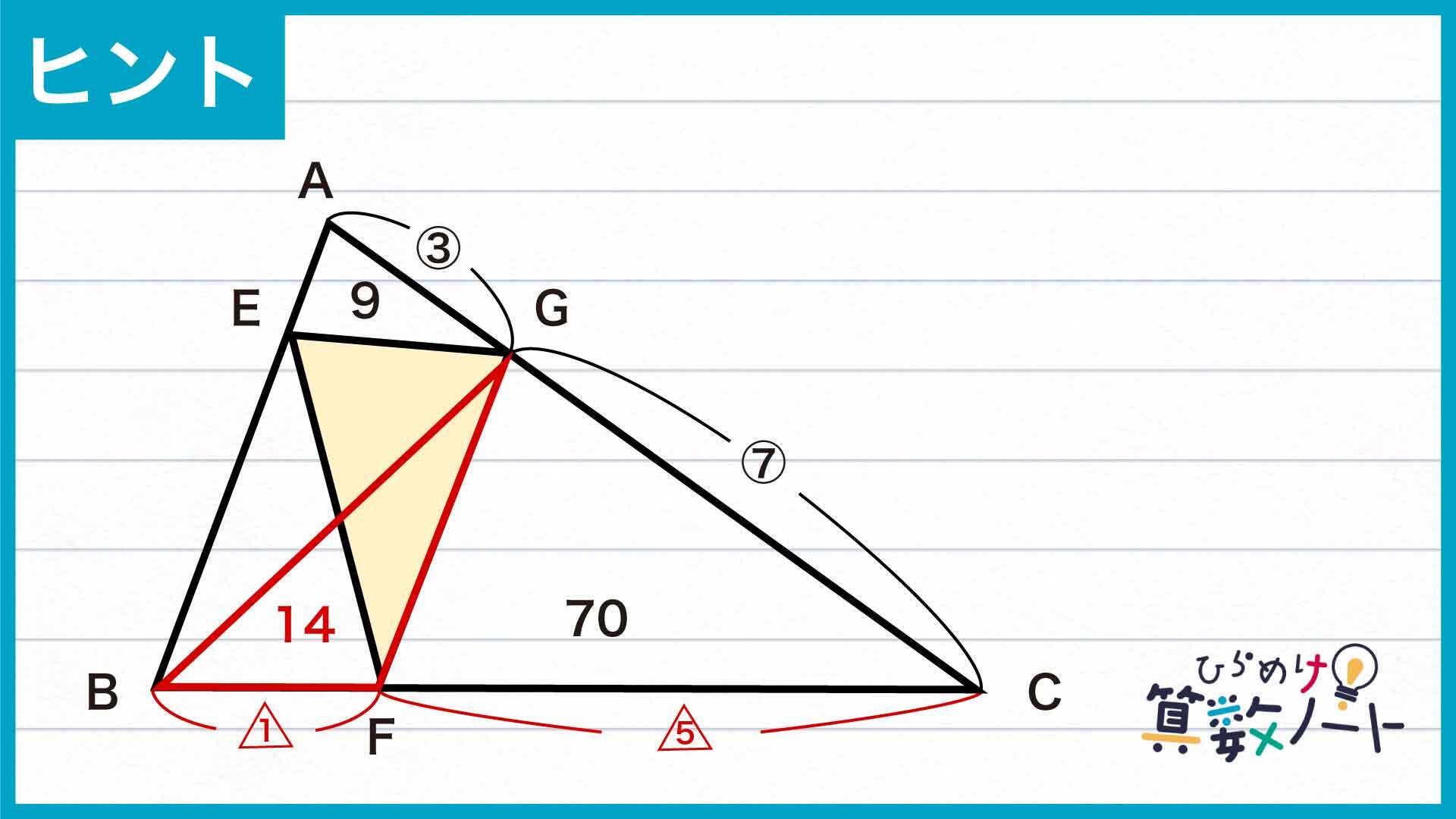
三角形ABGと三角形CBGはAG、GCを底辺としたときの高さが等しく、面積比は底辺の長さの比から3:7です。三角形ABCの面積が120なので、三角形CBGの面積は120÷10×7=84だとわかります。
したがって、三角形GBFの面積は84-70=14です。ここで三角形GBFと三角形GFCに注目してみると、2つの三角形はBF、FCを底辺としたときの高さが等しく、その面積比は14:70=1:5です。したがって、底辺の長さの比についてもBF:FC=1:5が成り立つのです。

















.jpg)






