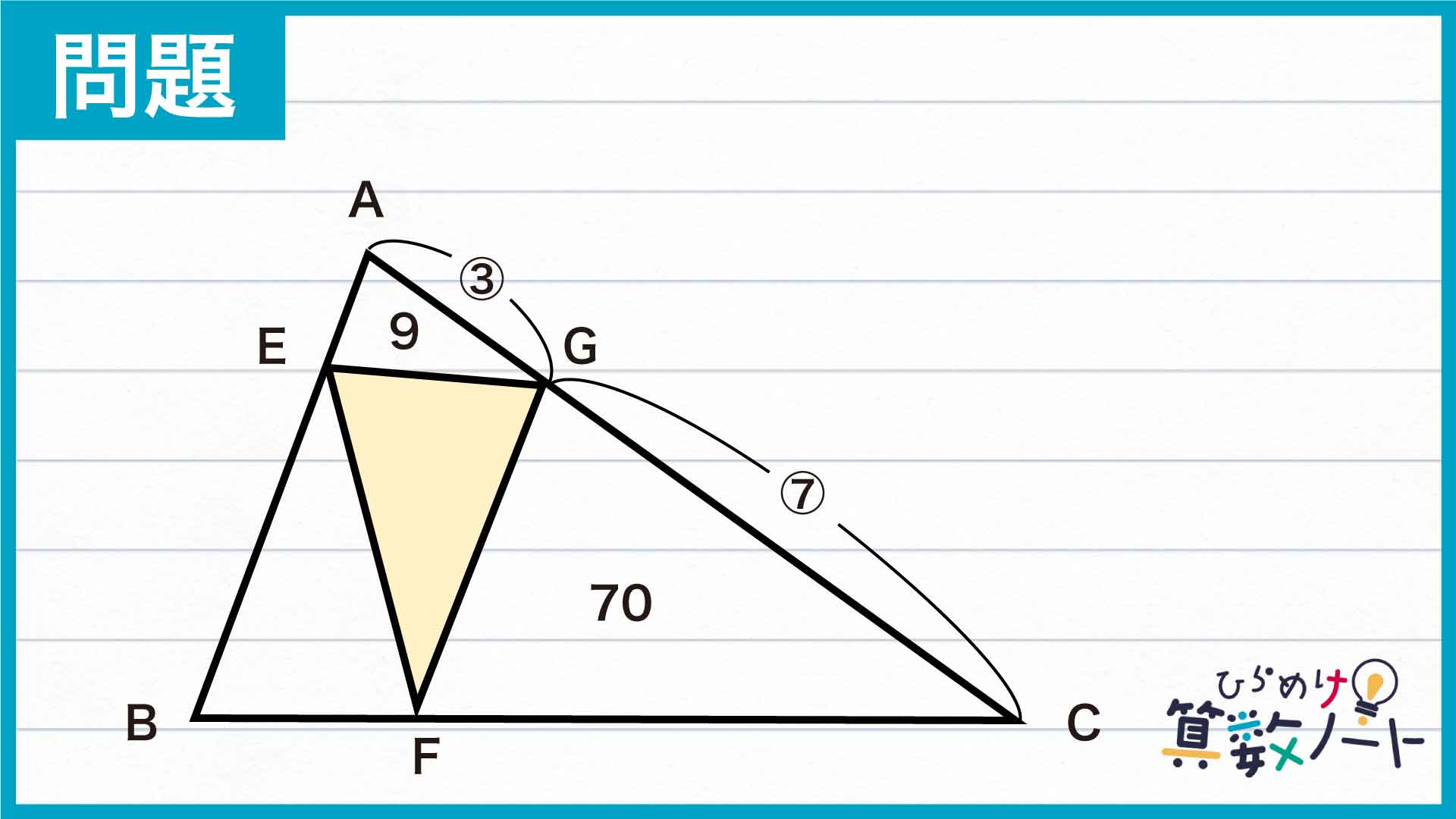
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
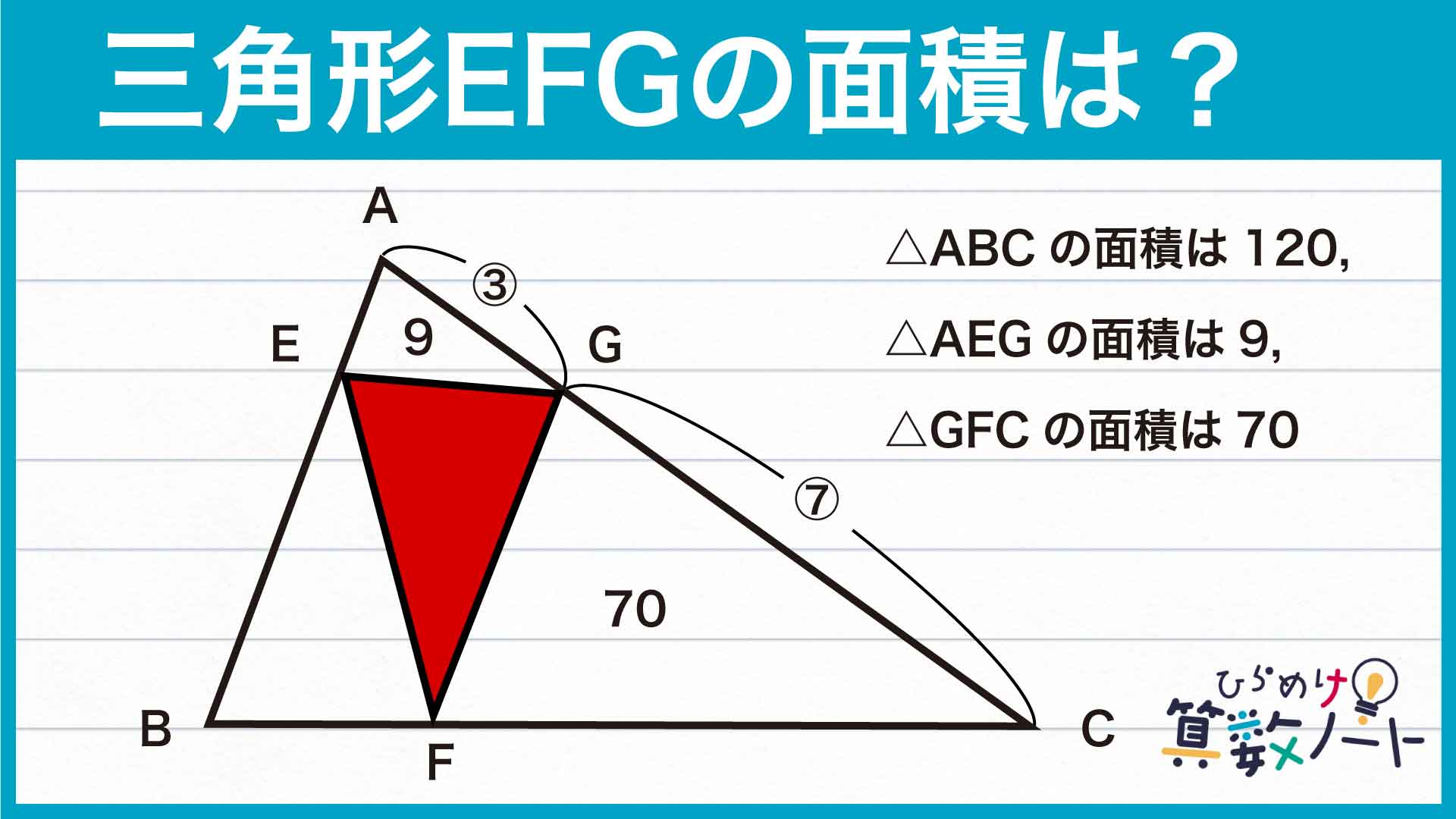
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
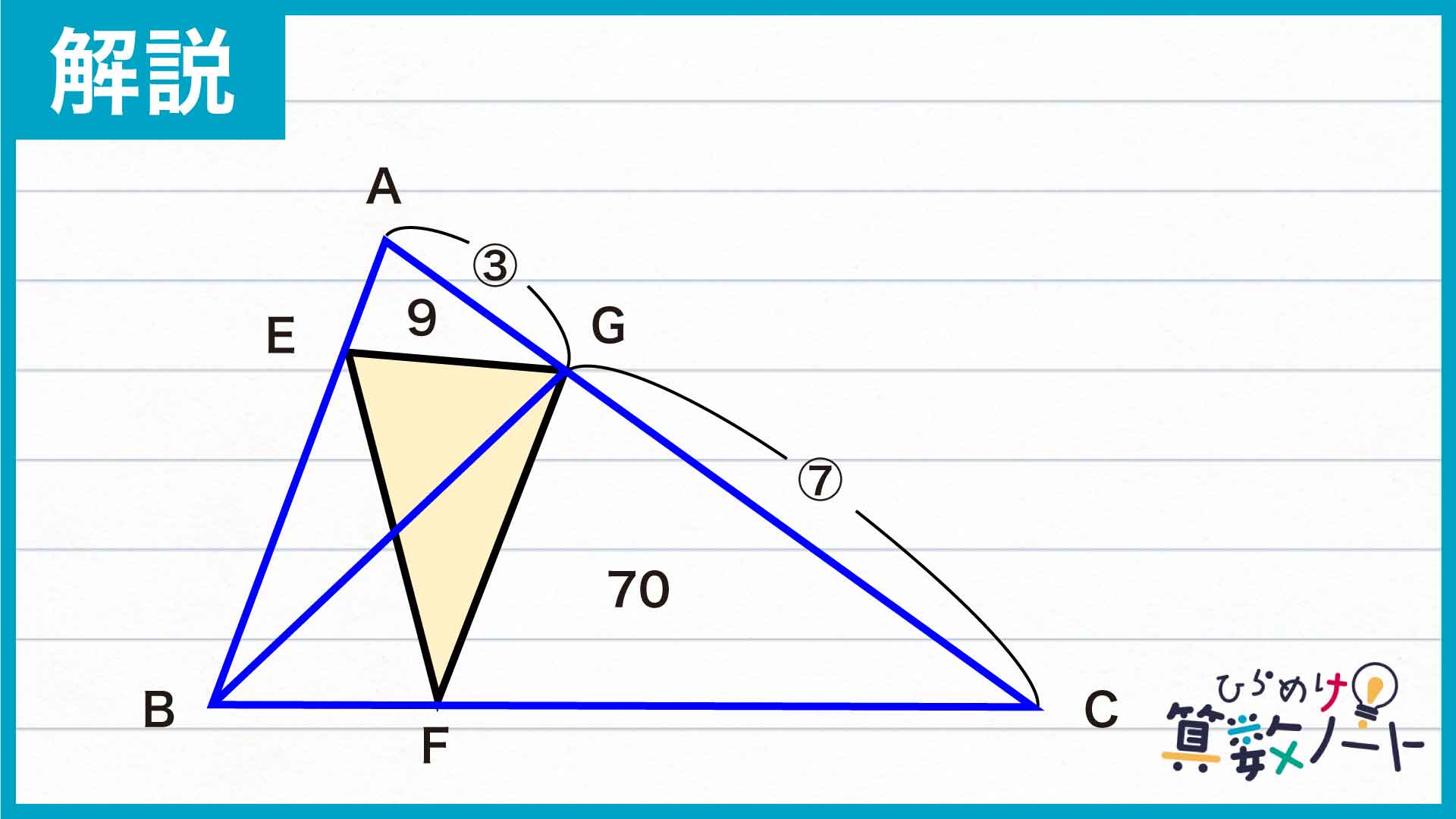
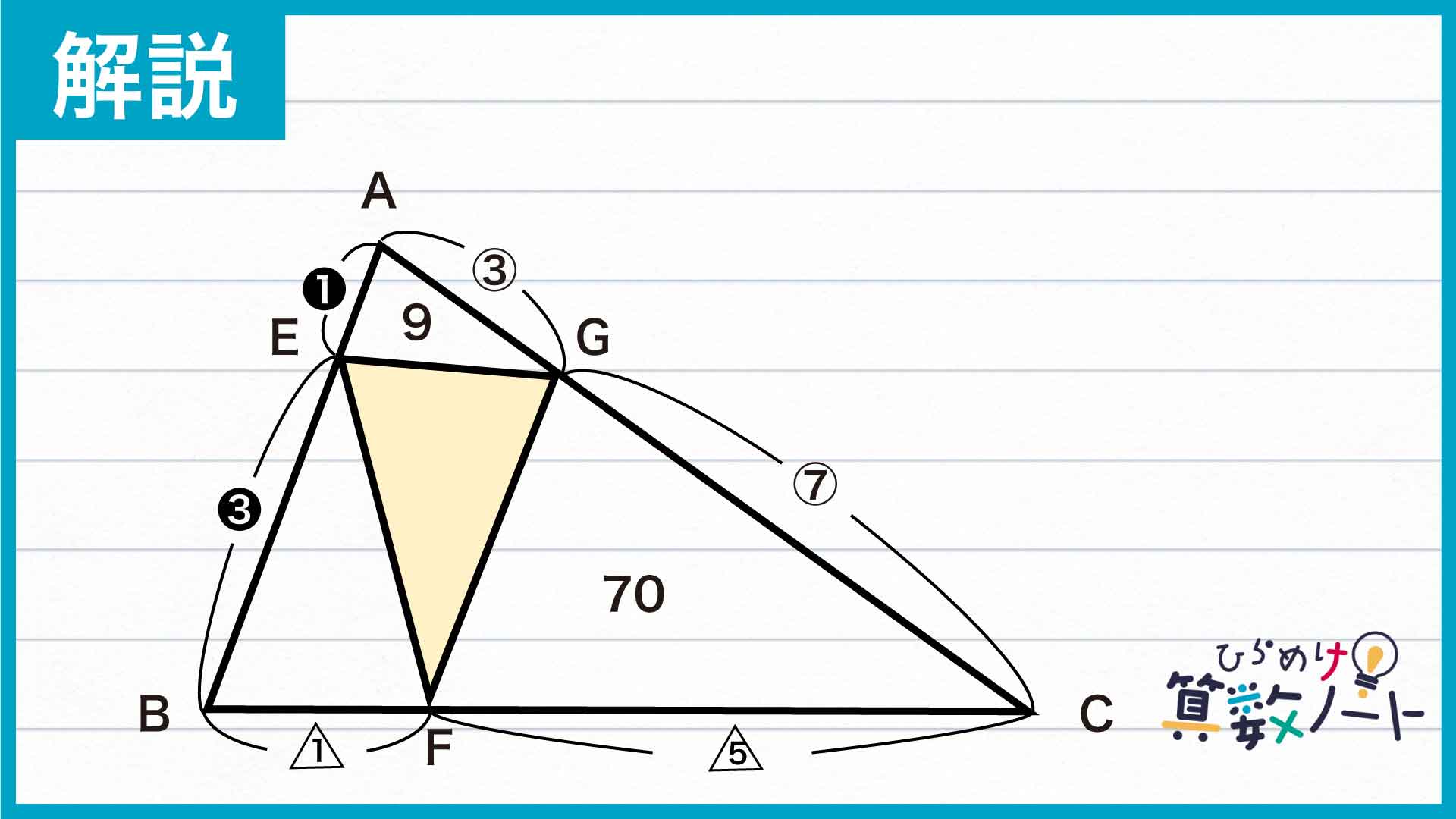
この問題の解き方をまとめた図がこちらです。
ポイントは、辺の長さの比を活かせるように三角形を分割し直すことです。
では、このポイントを踏まえつつ解いていきましょう!
三角形を分割し直す
今回の問題を解く際に重要なのは、「高さの等しい三角形の面積比が底辺の長さの比に等しくなる」という考え方です。問題文中ではAG:GCの比が与えられているので、これを活かすため下の図のように三角形を分割し直してみましょう。
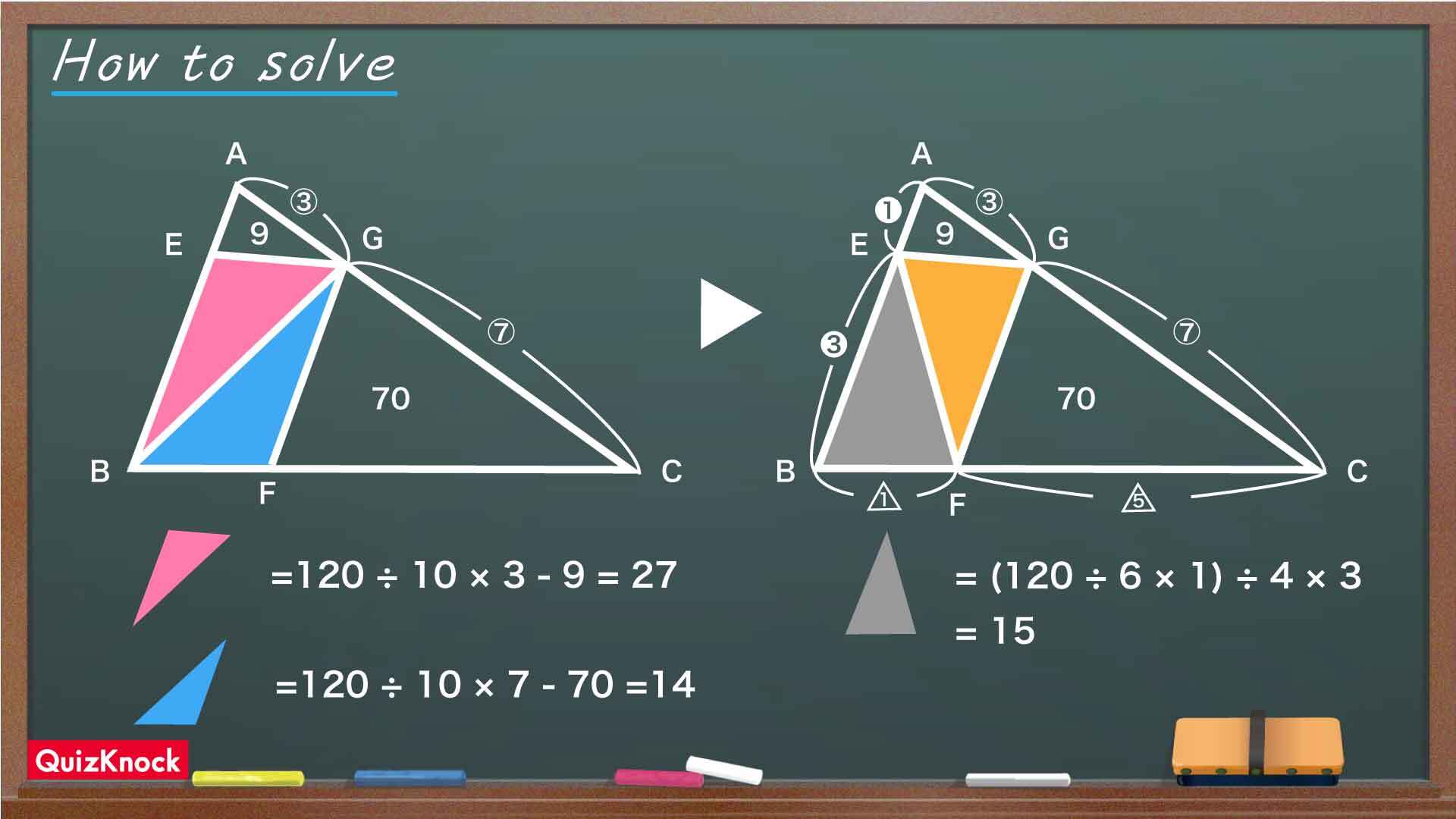
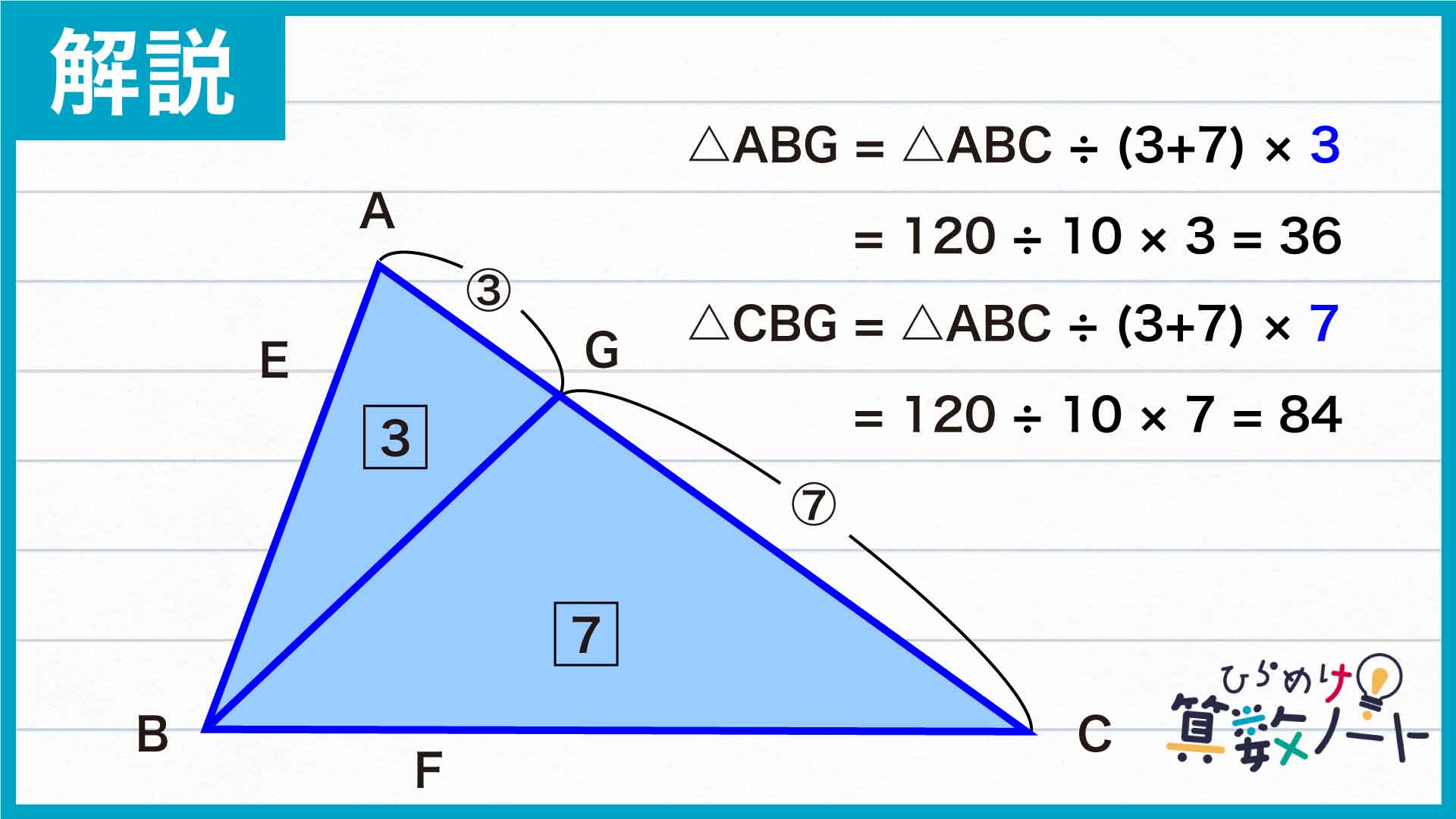
三角形ABGと三角形CBGはAG、GCを底辺としたときの高さが等しいことから、面積比は底辺と同じく3:7です。三角形ABCの面積が120なので、三角形CBGの面積は120÷10×7=84であるとわかります。
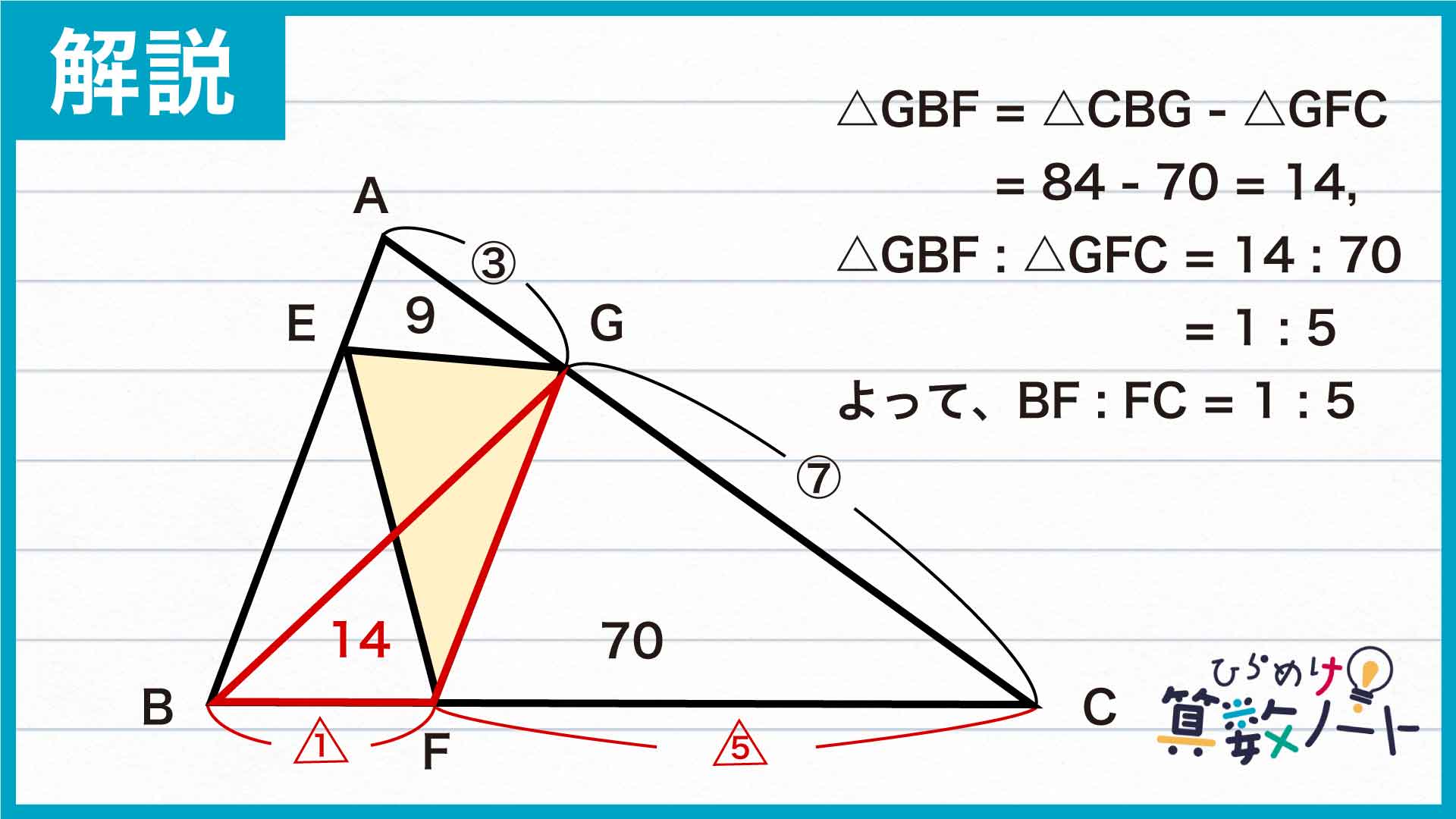
次に、三角形GBFと三角形GFCに注目します。三角形GBFの面積は84-70=14なので、2つの三角形の面積比は三角形GBF:三角形GFC=14:70=1:5です。三角形GBFと三角形GFCはBF、FCを底辺としたときの高さが等しいことから、BF:FC=1:5が成り立ちます。
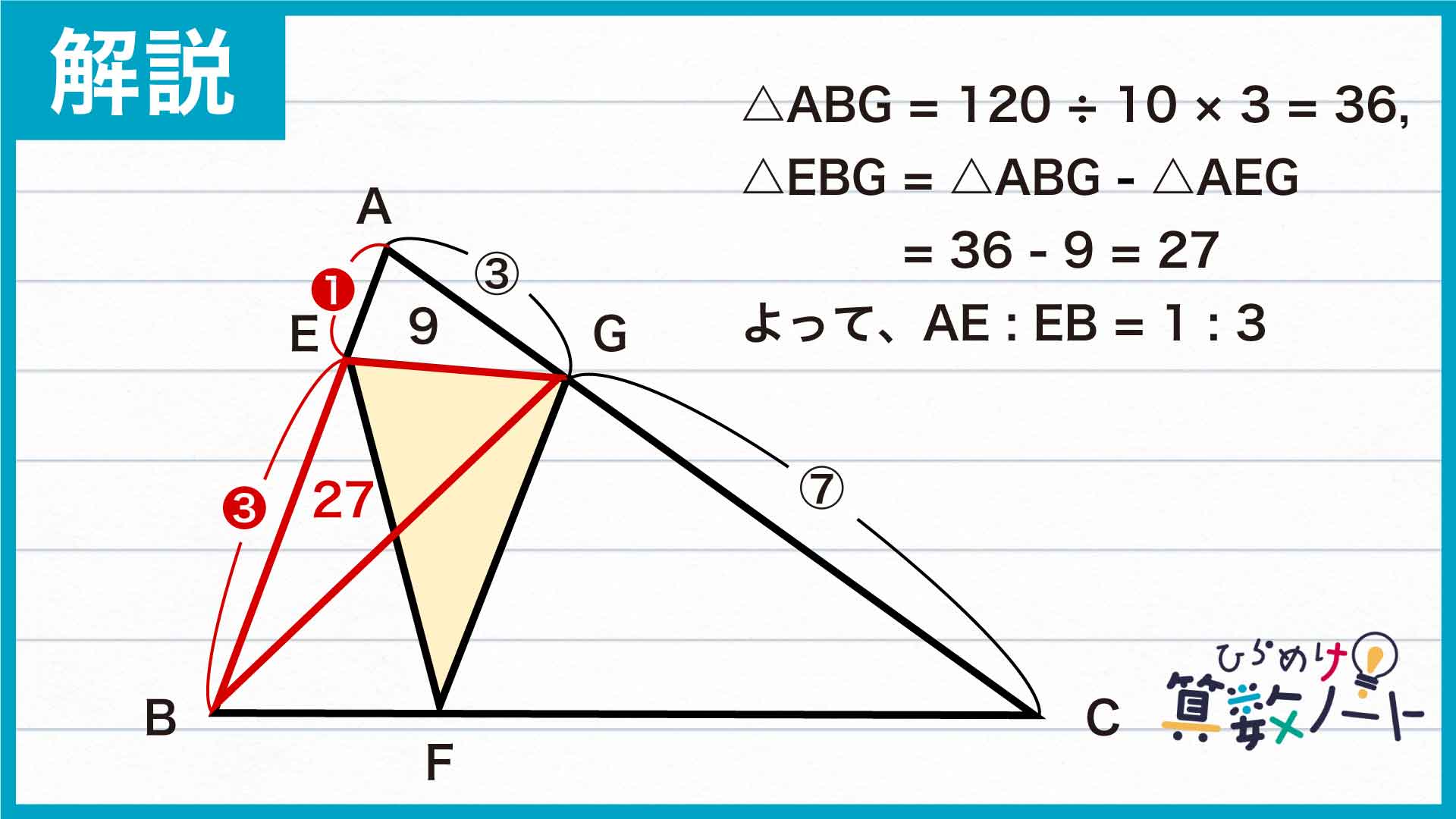
同様の手順でAE:EBを求めてみましょう。三角形ABGの面積は、120÷10×3=36です。三角形AEGと三角形EBGに注目すると、三角形EBGの面積が36-9=27であることから2つの三角形の面積比は三角形AEG:三角形EBG=9:27=1:3です。三角形AEGと三角形EBGはAE、EBを底辺としたときの高さが等しいことから、AE:EB=1:3が成り立ちます。
周囲の三角形の面積を求める
ここまでの計算から、分割された三角形ABCの各辺において以下のような長さの関係が成り立ちます。
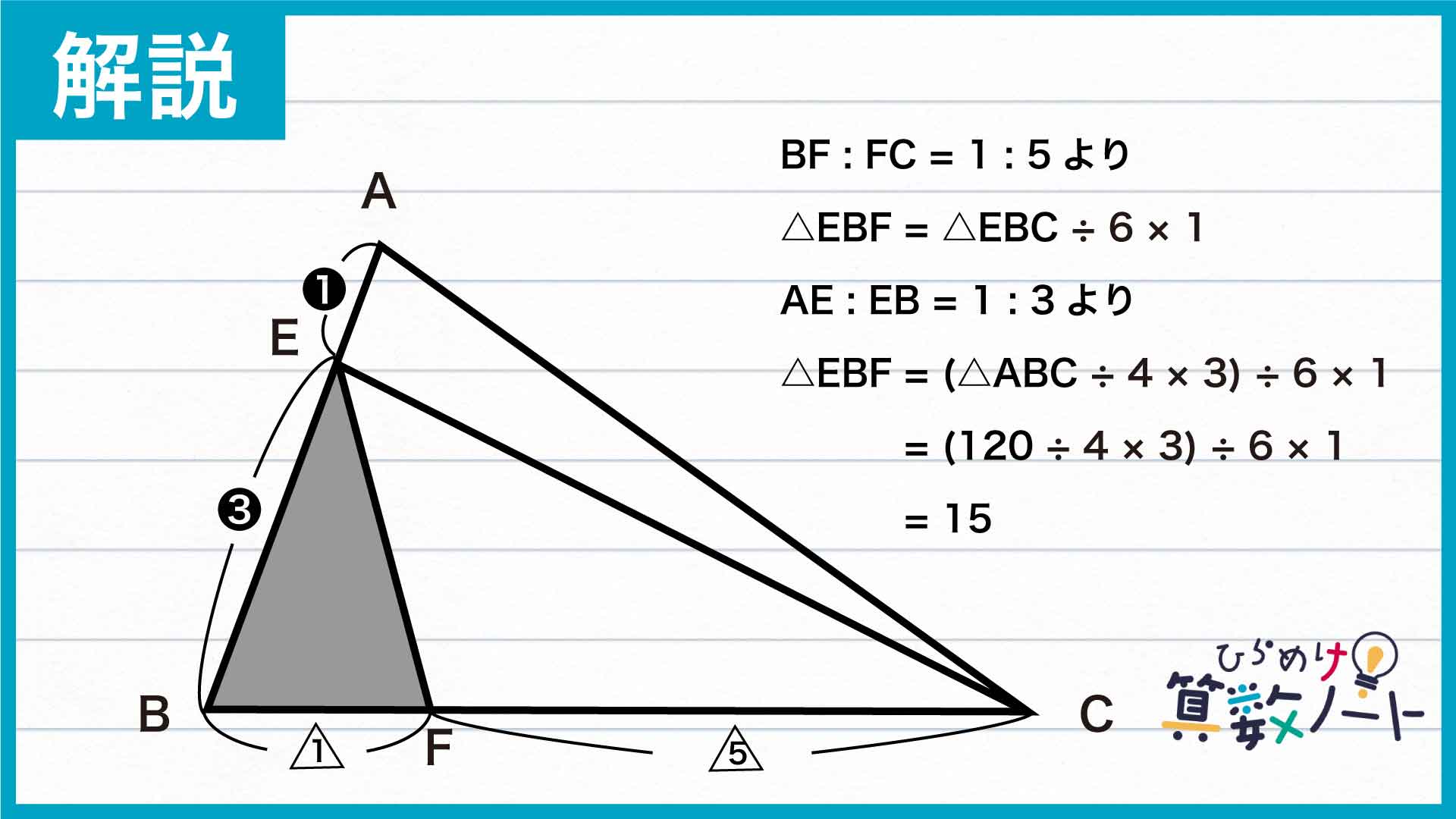
これらの比を用いることで、三角形EBFについても面積を求めることができます。
下の図より、AE:EB=1:3、BF:FC=1:5なのでこれらの比を面積比に一気に当てはめると、三角形EBFの面積は120÷4×3÷6×1=15となります。
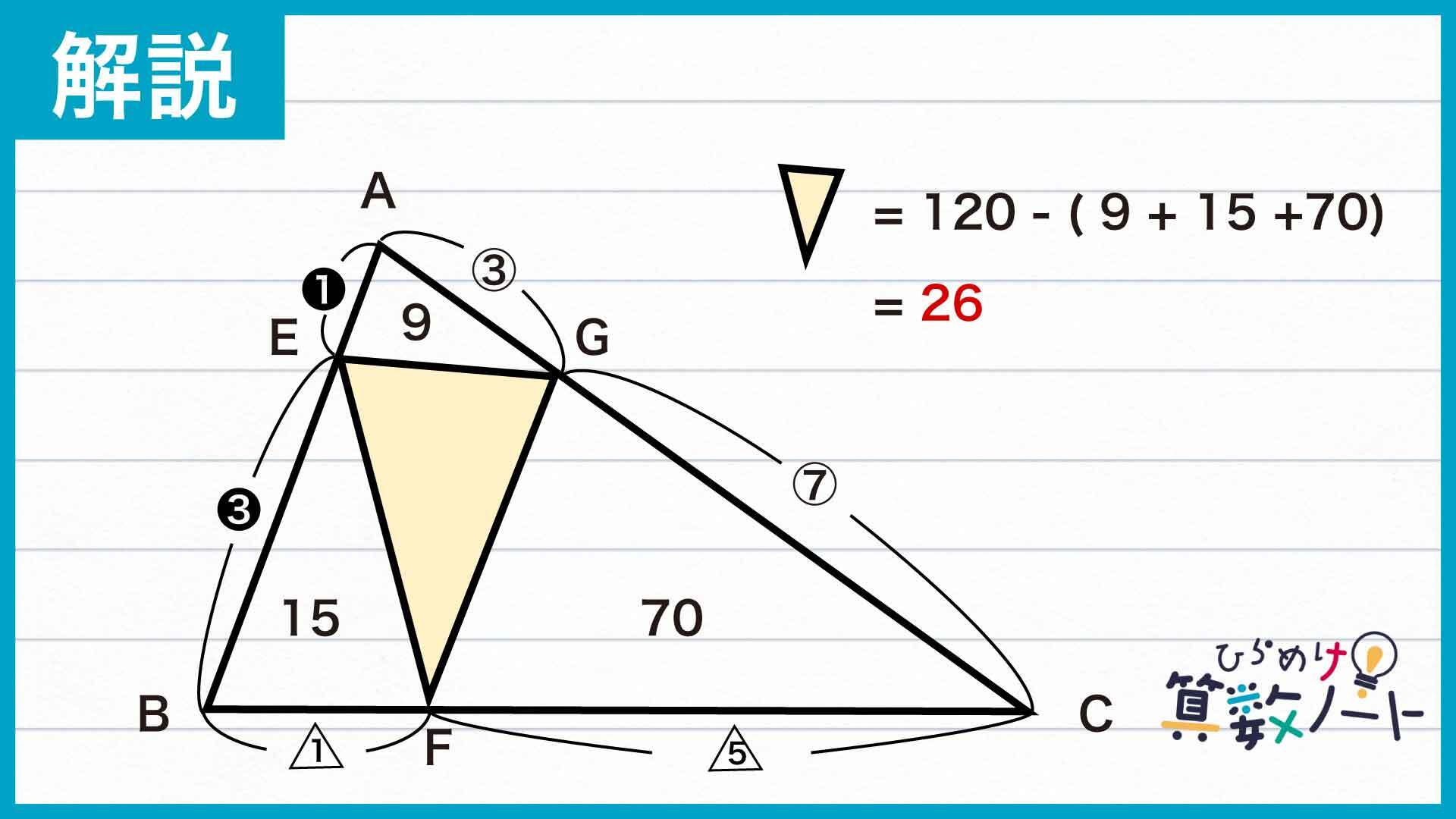
これで、塗りつぶされた三角形EFGを除く全ての部分の面積を求めることができました。
したがって、求める三角形EFGの面積は120-(9+15+70)=26であるとわかるのです。
答え:26
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)







.jpg)







