小学4年生で解ける「台形の面積」の問題。あなたは解けますか？

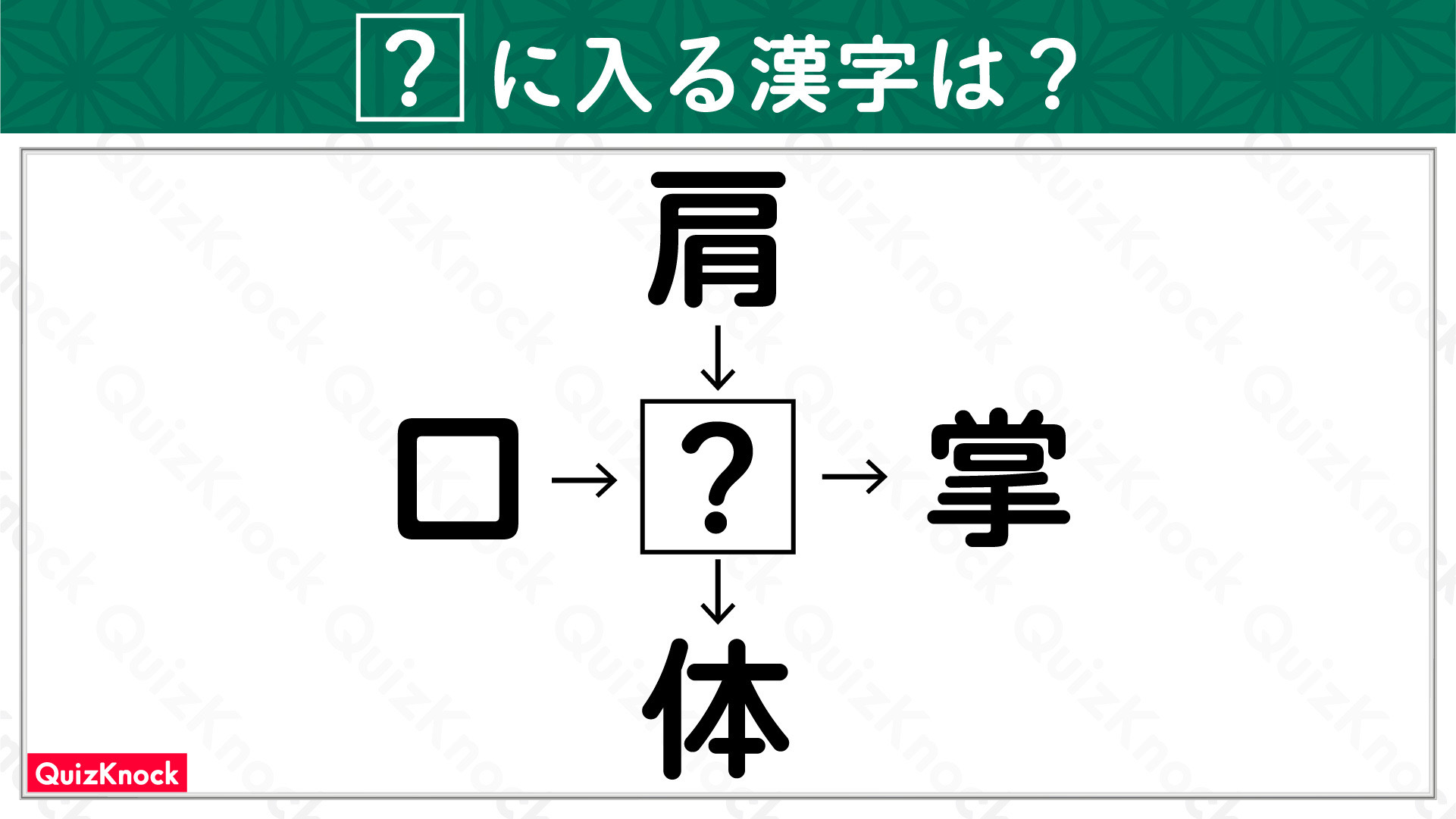
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：自力で解きたい方はこちらへ！ 以下は問題の解説です

今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、

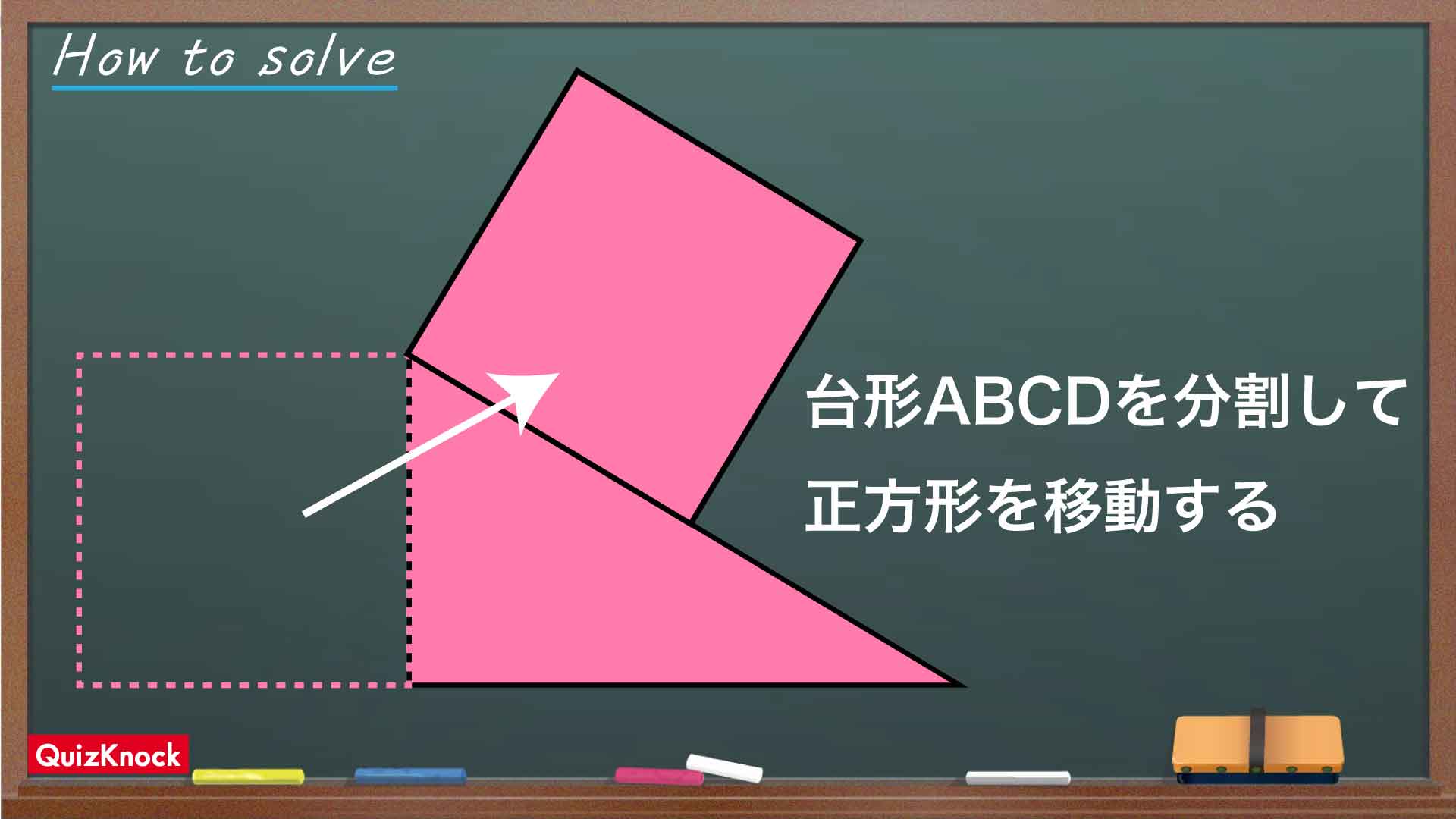
• 台形ABCDを分割して、正方形の部分を移動させる
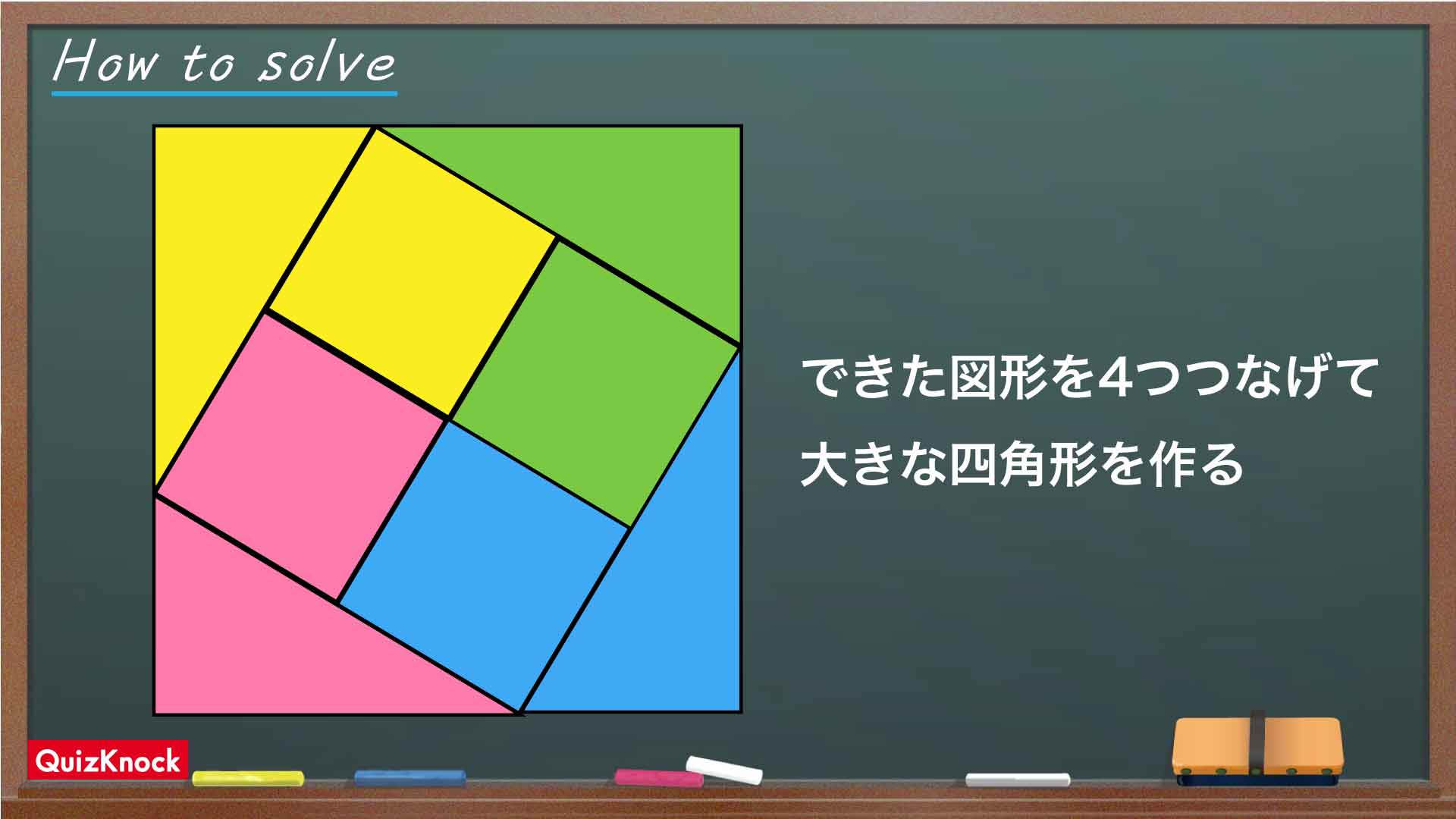
• できた図形を4つつなげて、大きな正方形を作る

の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。

台形ABCDを分割して、正方形の部分を移動させる

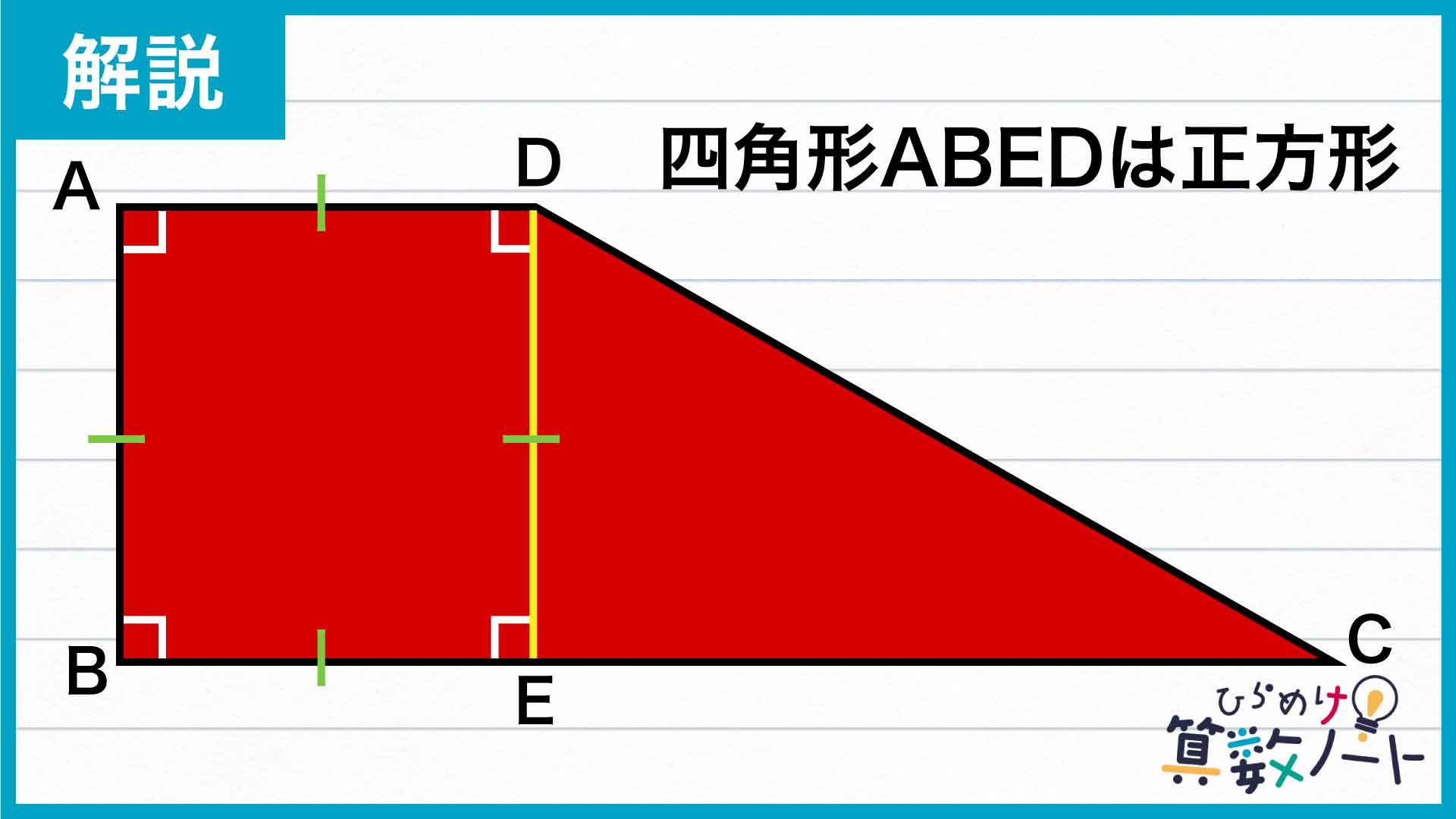
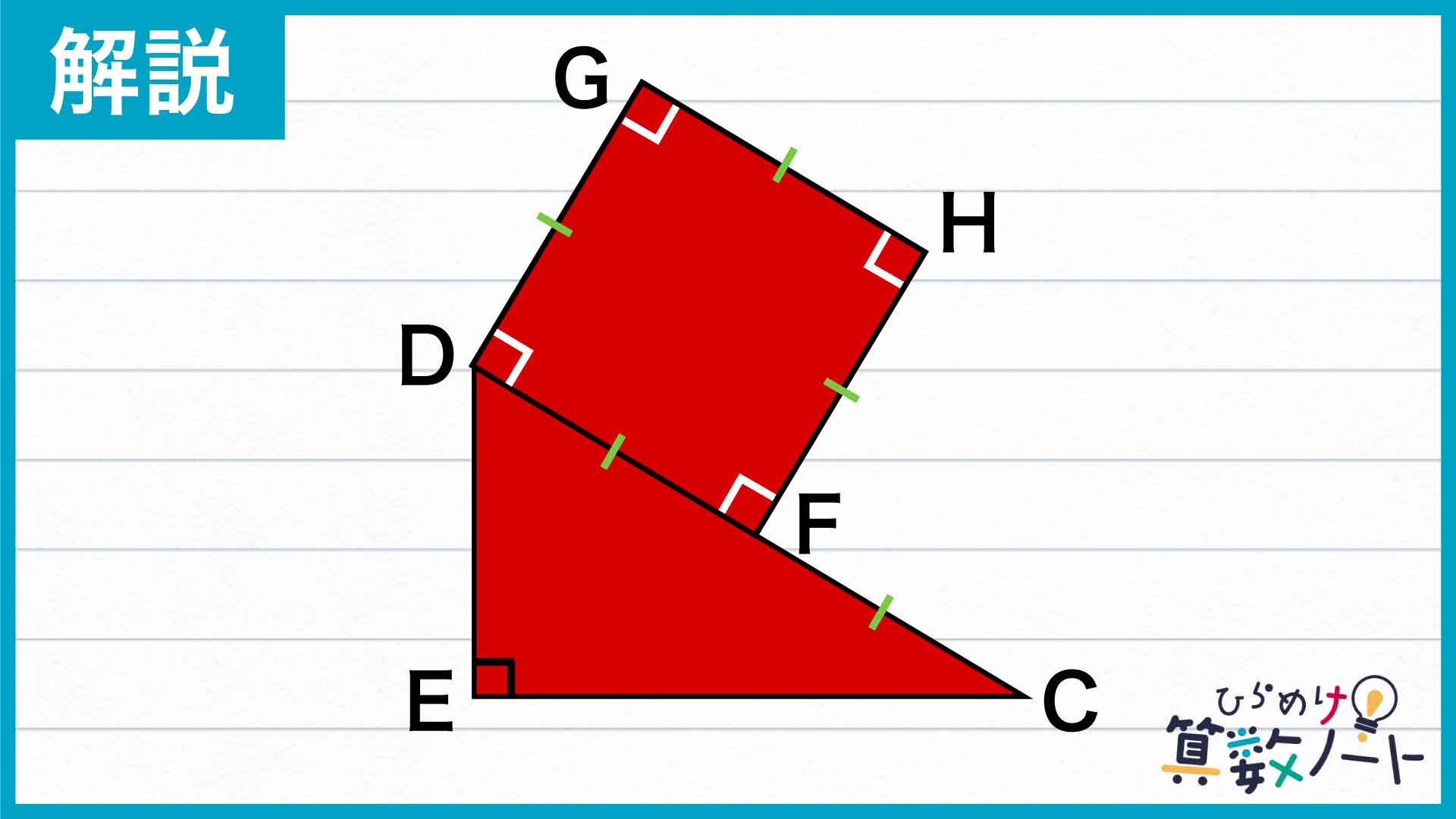
下の図のように、点Dから辺BCに垂直に線を引きます。辺BCとこの垂直な線の交点を点Eとすると、四角形ABEDは4つの内角の大きさが全て90度になるうえ、辺ABと辺ADの長さが等しいため、この四角形は正方形になります。また、三角形DECは角DECが90度の直角三角形です。

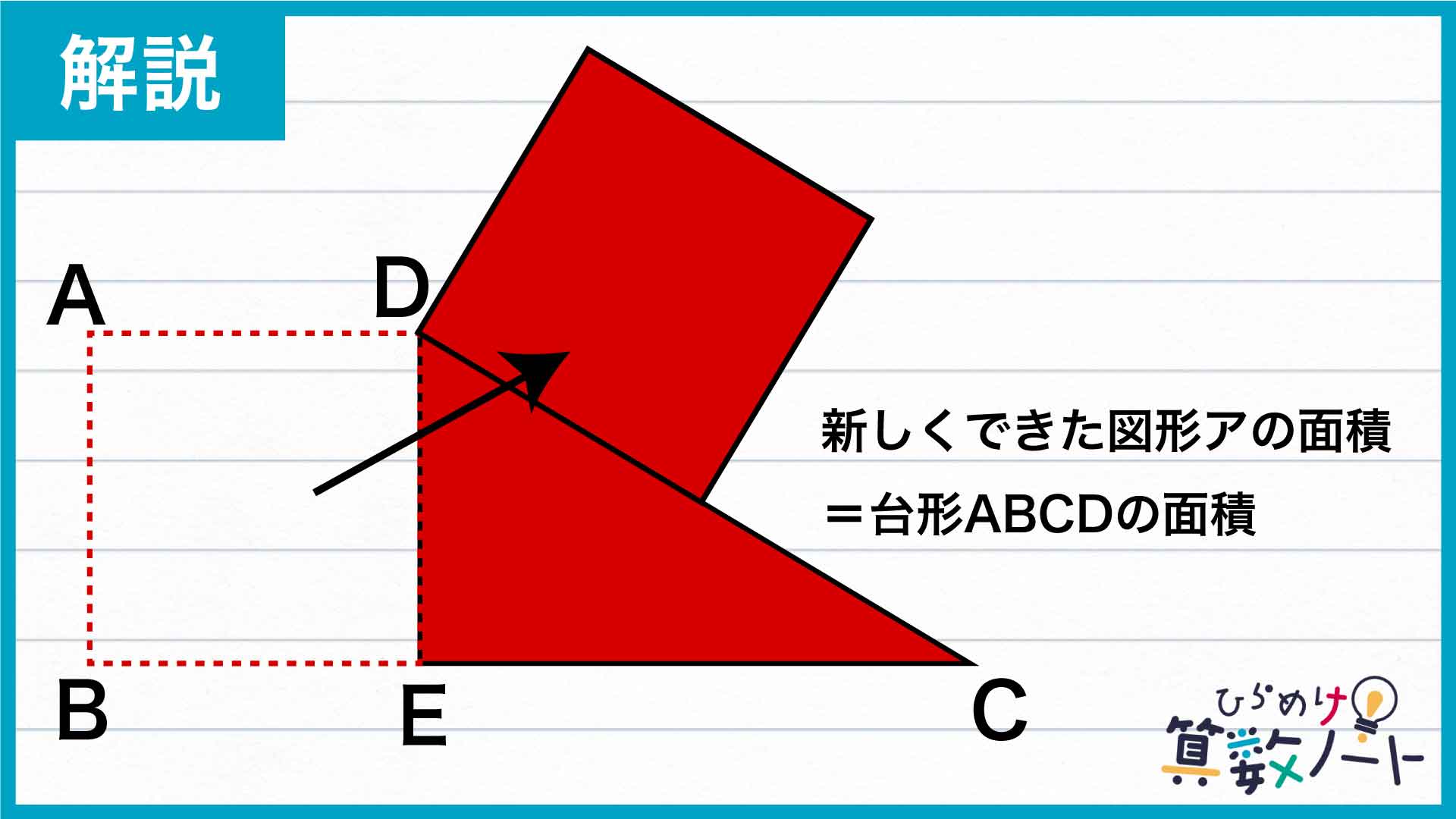
さらに、下の図のように正方形ABEDを辺CDに取りつけます。完成した図形を「図形ア」とすると、図形アの面積はもとの台形ABCDの面積は等しいです。よって、図形アの面積を求めれば台形ABCDの面積がわかります。

ここで、正方形ABEDを移動させた図形を正方形GHFDとします。問題文の条件から辺CDの長さは辺ADの長さの2倍なので、辺CDの長さは、「正方形GHFDの1辺の長さ」の2倍です。よって、図形アにおいて、CF=CD-DF=2×DF-DF=DFとなるのでCF=DF、つまりCFの長さも「正方形GHFDの一辺の長さ」と等しくなります。

できた図形を4つつなげて、大きな正方形を作る

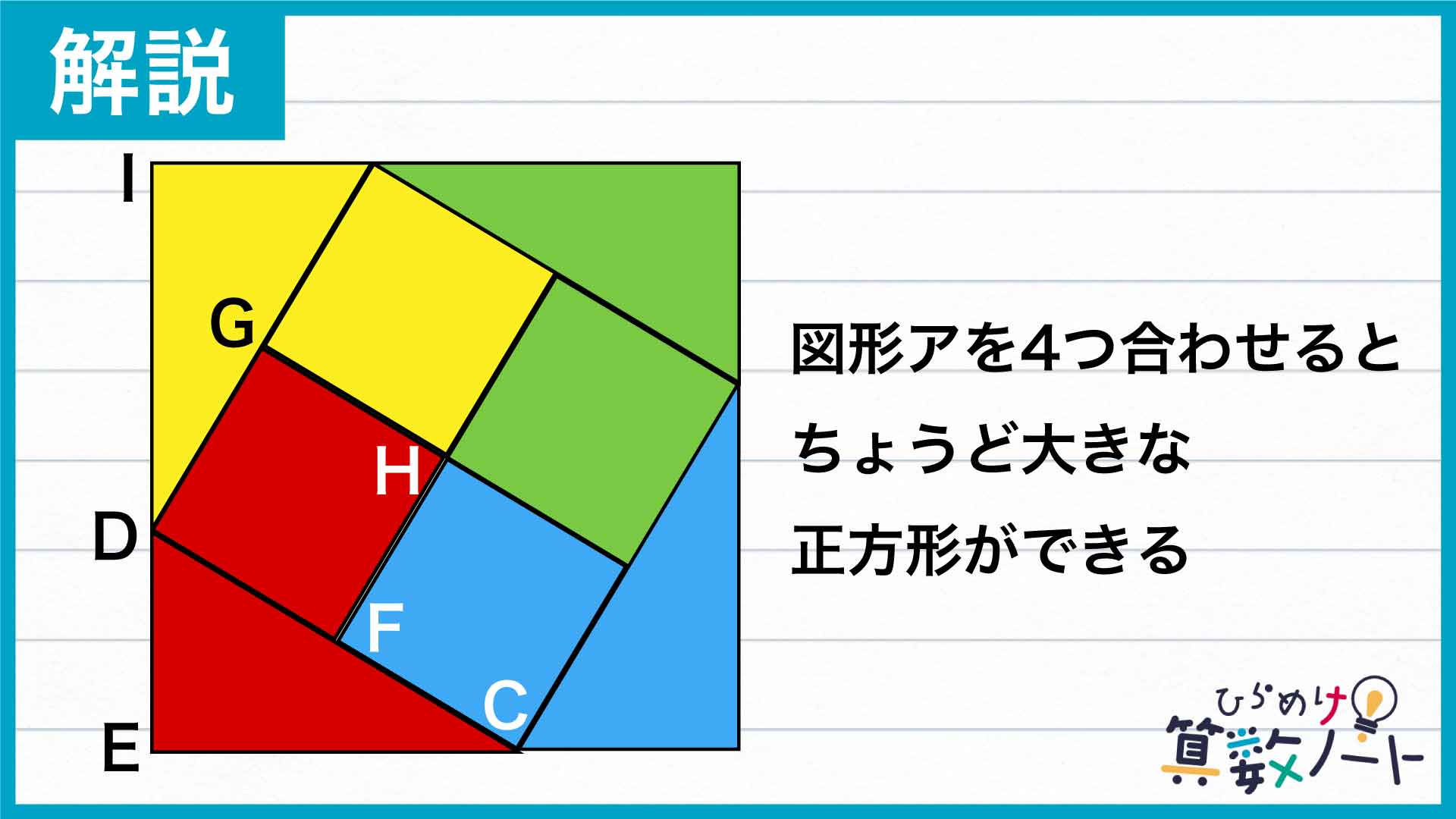
CFの長さと「正方形GHFDの4つの辺の長さ」が全て等しいことと、正方形GFHDの4つの角の大きさが全て90度であることから、下の図のように図形アをぴったりを4つつなげることができます。

また、DCの長さがDEの長さの2倍であるため、三角形CDEの3つの角の大きさはそれぞれ30度、60度、90度です。さらに上の図で、

• 角CDE+角DEC+角DCE=180度（直角三角形DECの内角の和）
• 角CDE+角GDF+角IDG=180度
• 角DEC=角GDF=90度

であることから角DCE=角IDGであり、隣り合う2つの図形アが一直線上に並ぶため、図形アを4つ合わせてできる図形はちょうど大きな四角形になることがわかります。ここでできた四角形を「大きな四角形」と呼びます。

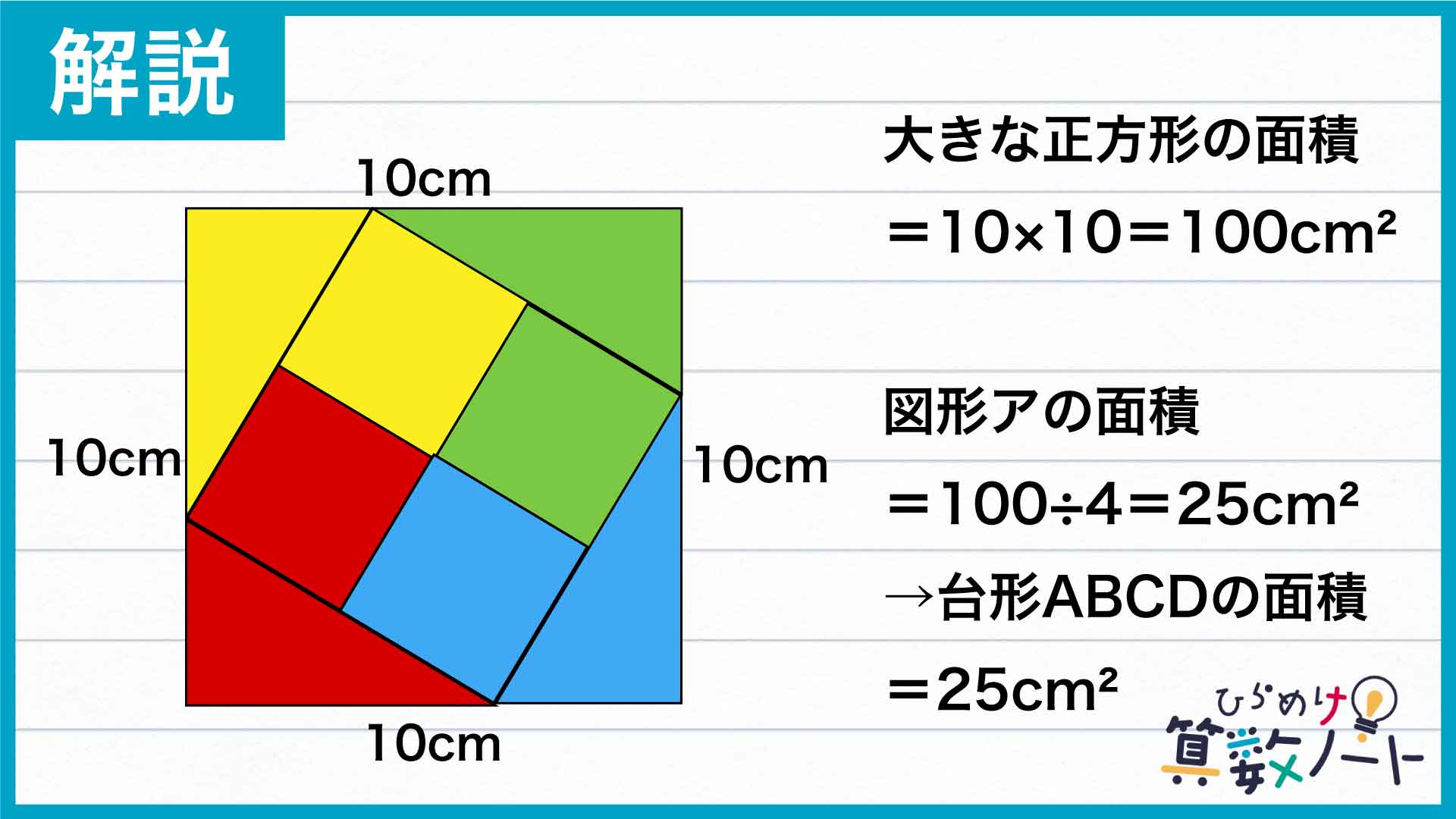
さらに、この「大きな四角形」の4辺の長さは、元の三角形における辺BCの長さと等しくなります。問題文からこの長さは10cmなので、「大きな四角形」は1辺の長さが10cmの正方形であることがわかります。よって、「大きな四角形」の面積は10×10=100cm²です。

「大きな四角形」は、図形アの面積4つ分なので、図形アの面積は100÷4=25cm²になります。よって、求める台形ABCDの面積は、図形アの面積と等しいことから25cm²です。

答え：25cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】