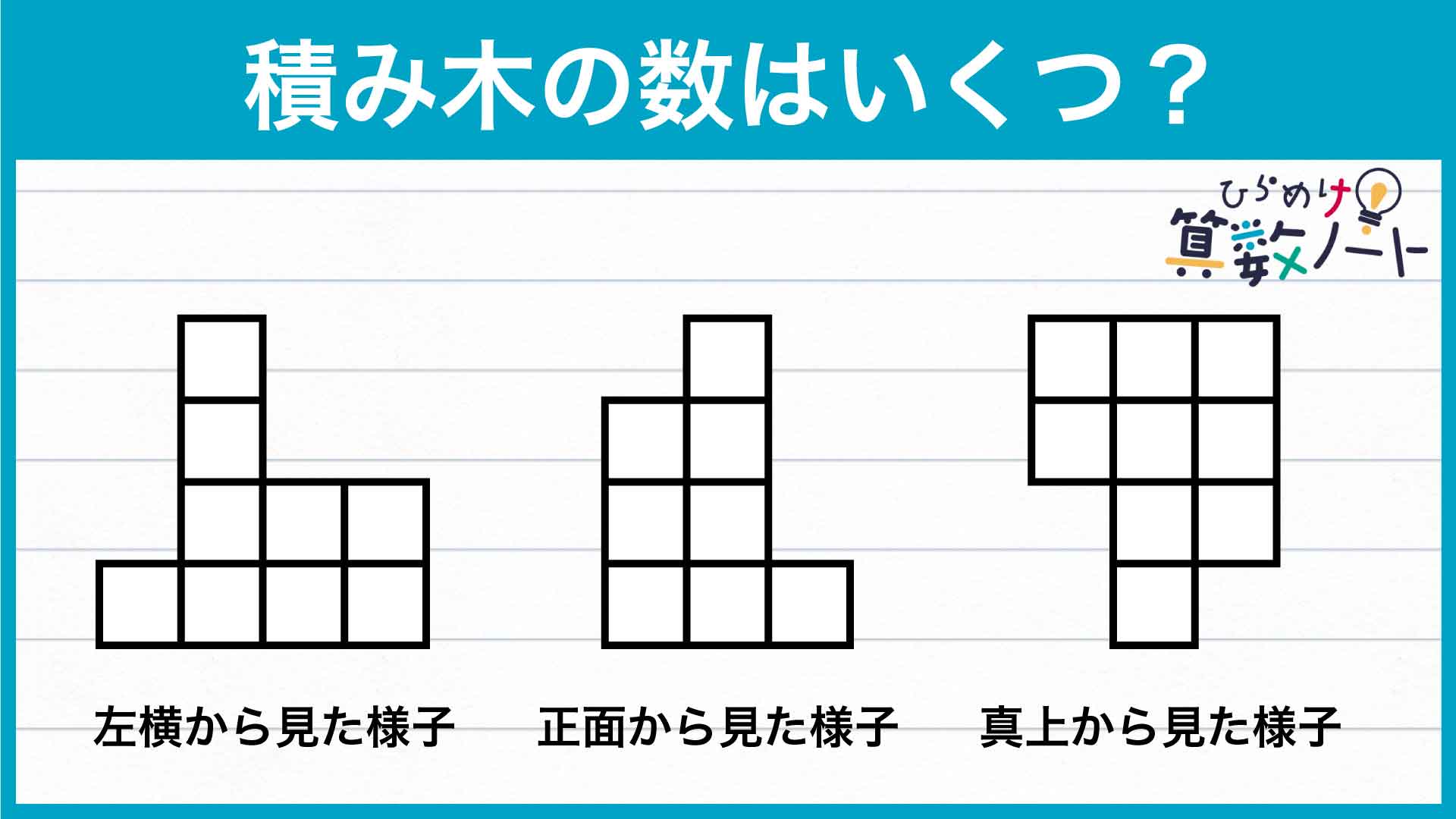
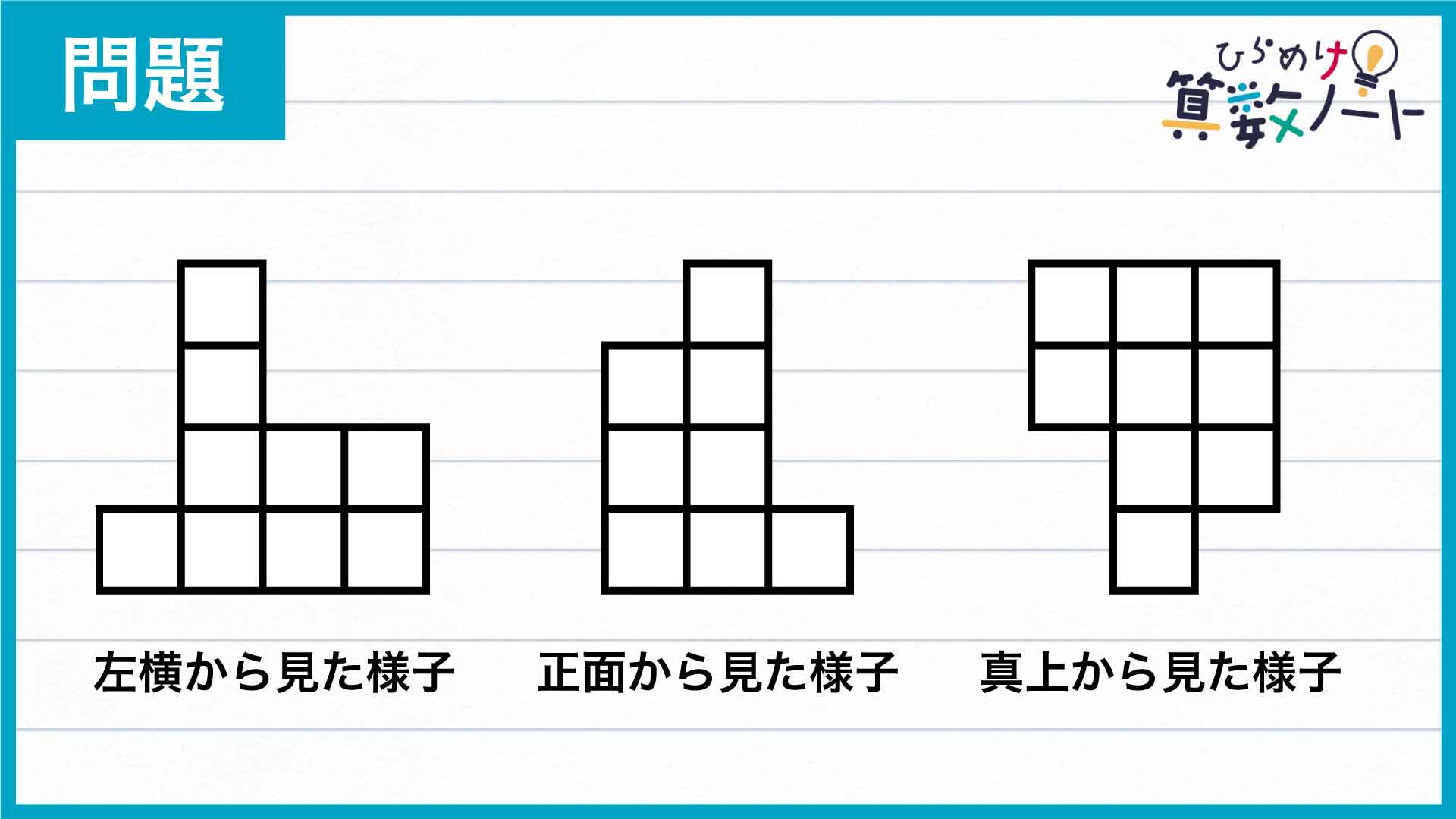
問題はこちら
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
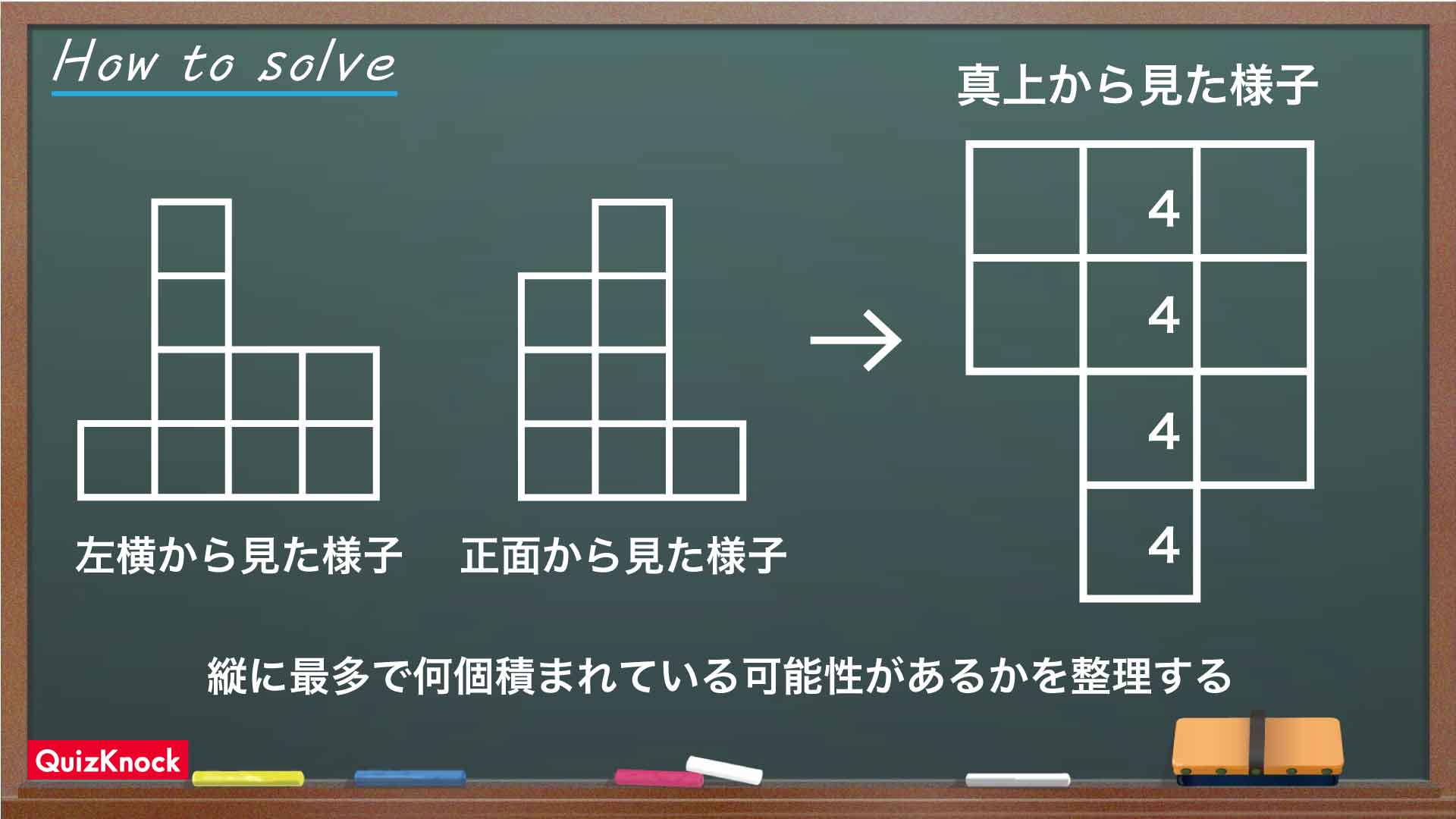
今回の解き方をまとめた図がこちらです。
今回のポイントは、「縦に積まれた数を、それぞれの図と照らし合わせながら絞り込む」ことです。
このポイントをもとに、問題を攻略していきましょう！
真上から見た図に書き込んでいく
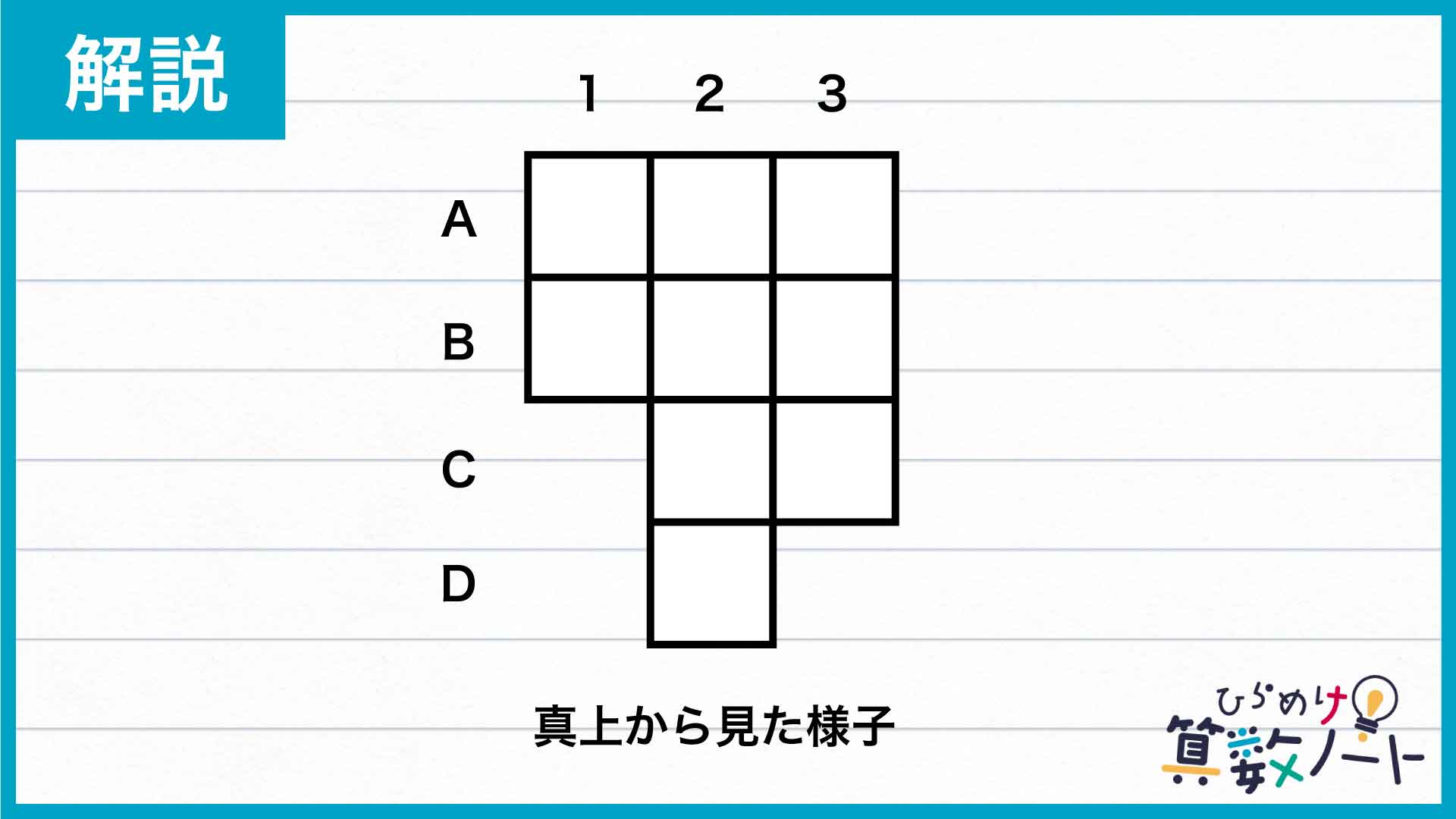
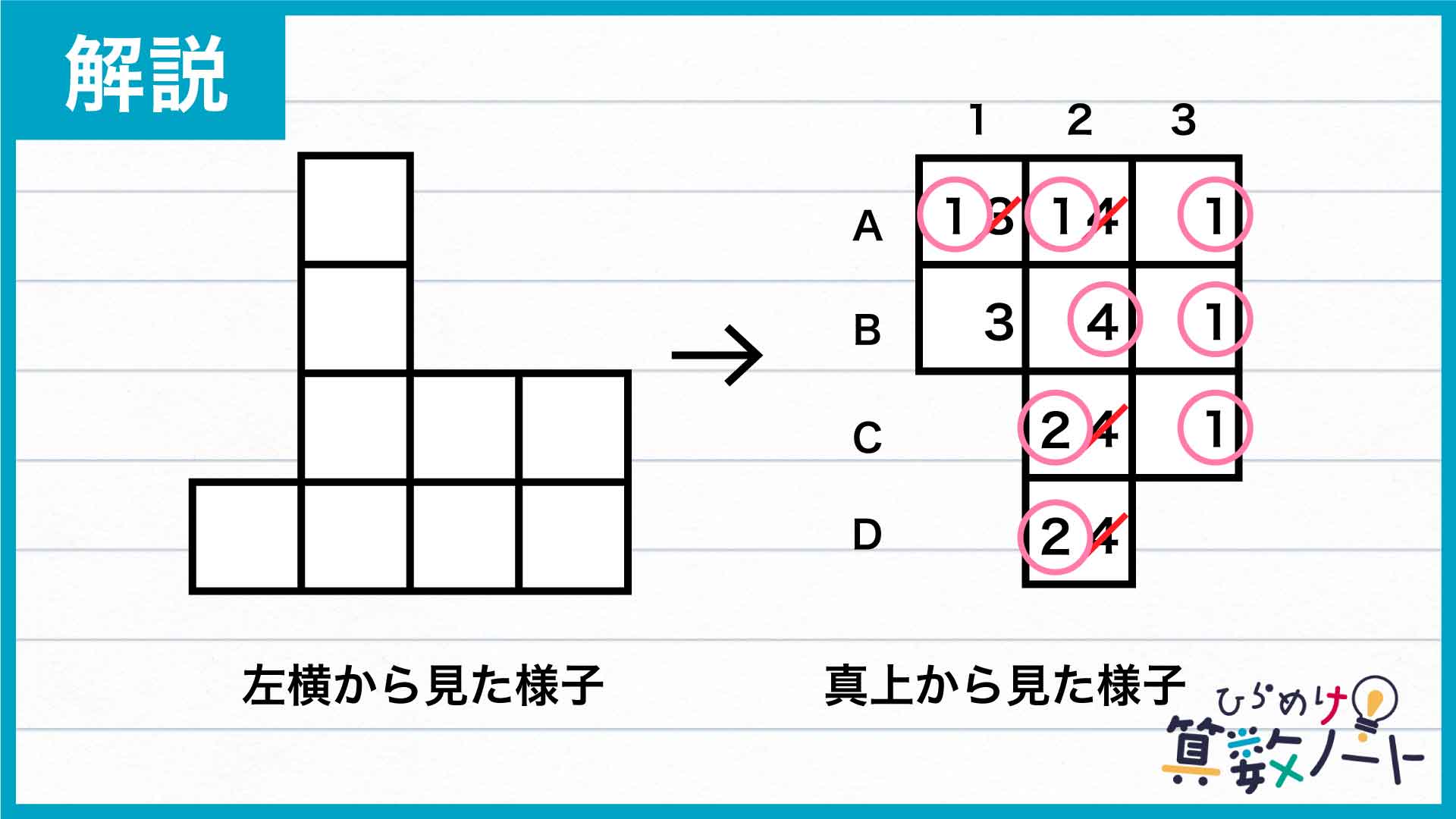
解説のため、真上から見た様子の行と列に、下の図のように番号とアルファベットを振ります。
正面から見た様子、左横から見た様子と照らし合わせ、各場所において縦に最多で何個積まれている可能性があるかを、真上から見た様子の図に書き込んでいきます。
正面から見た様子と照らし合わせる
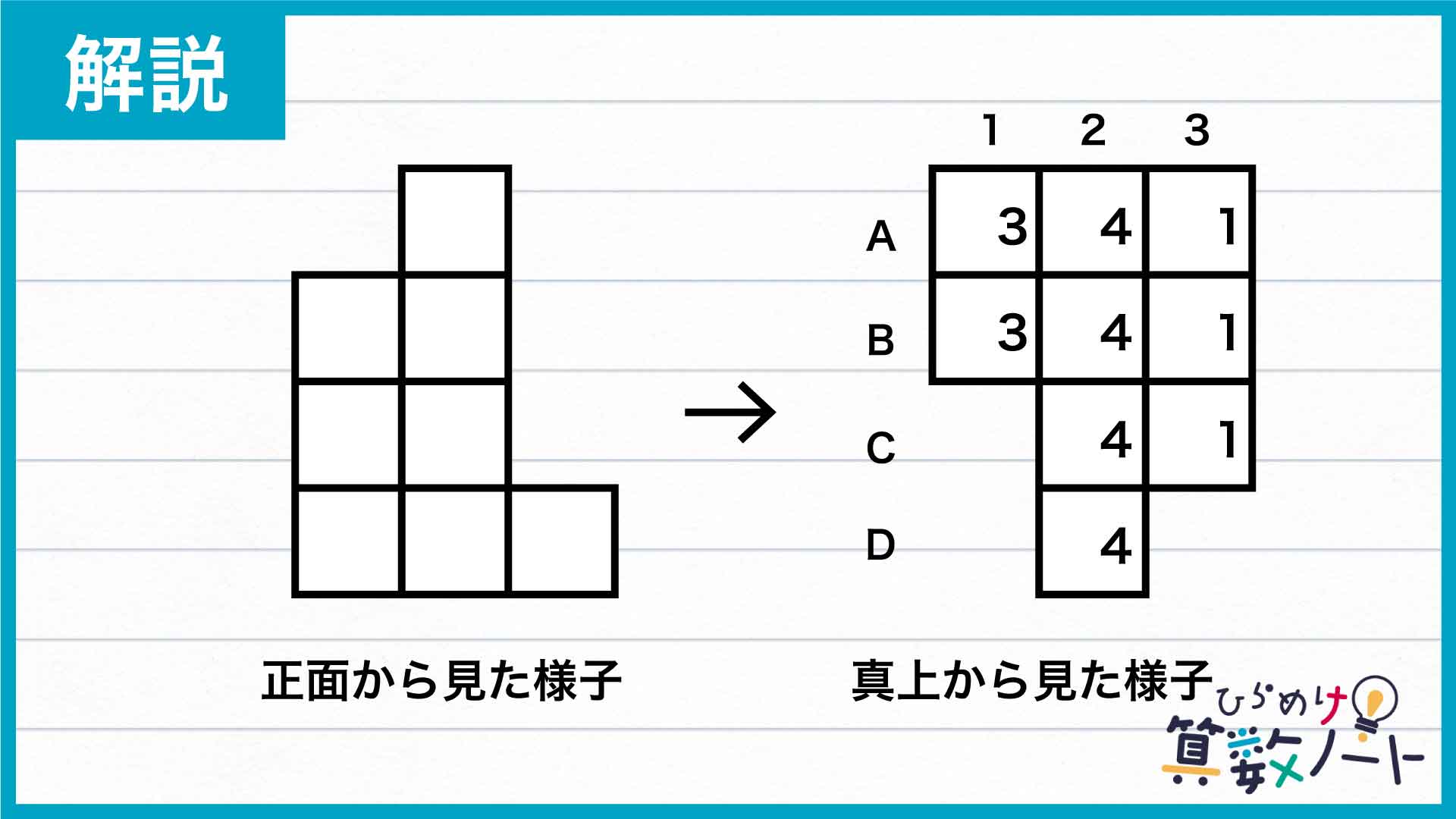
まずは、真上から見た様子と正面から見た様子を照らし合わせます。
正面から見た様子を見ると、1の列には最多で3個の積み木が積まれていることがわかります。同様に、2の列は4個、3の列は1個なので、下の図のように書き込んでいきます。
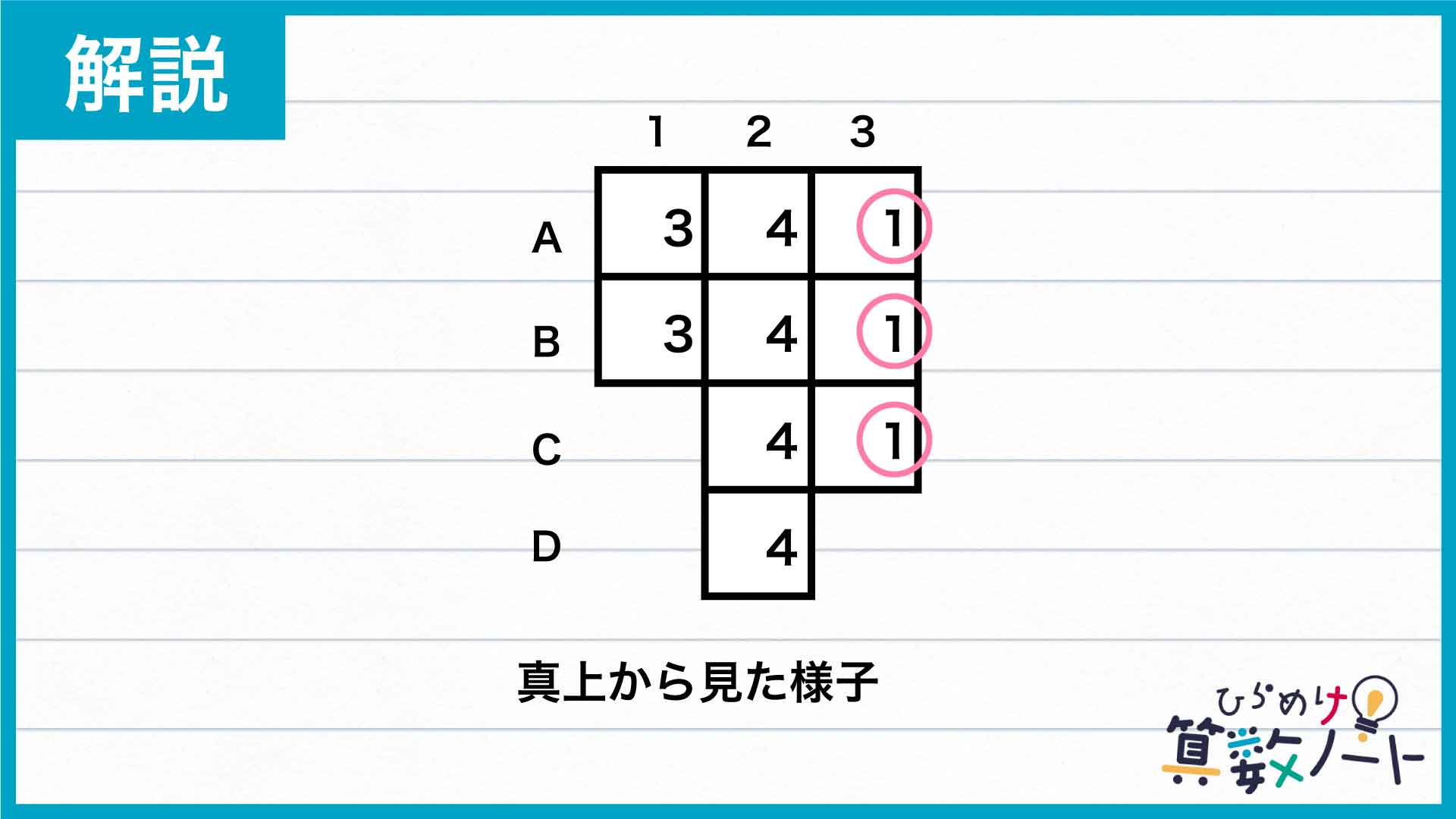
この時点で、3の列のA、B、Cの積み木は縦に1個だけであることが確定します。縦に積まれた積み木の数が確定したところは、数を丸で囲って印をつけます。
左横から見た様子と照らし合わせる
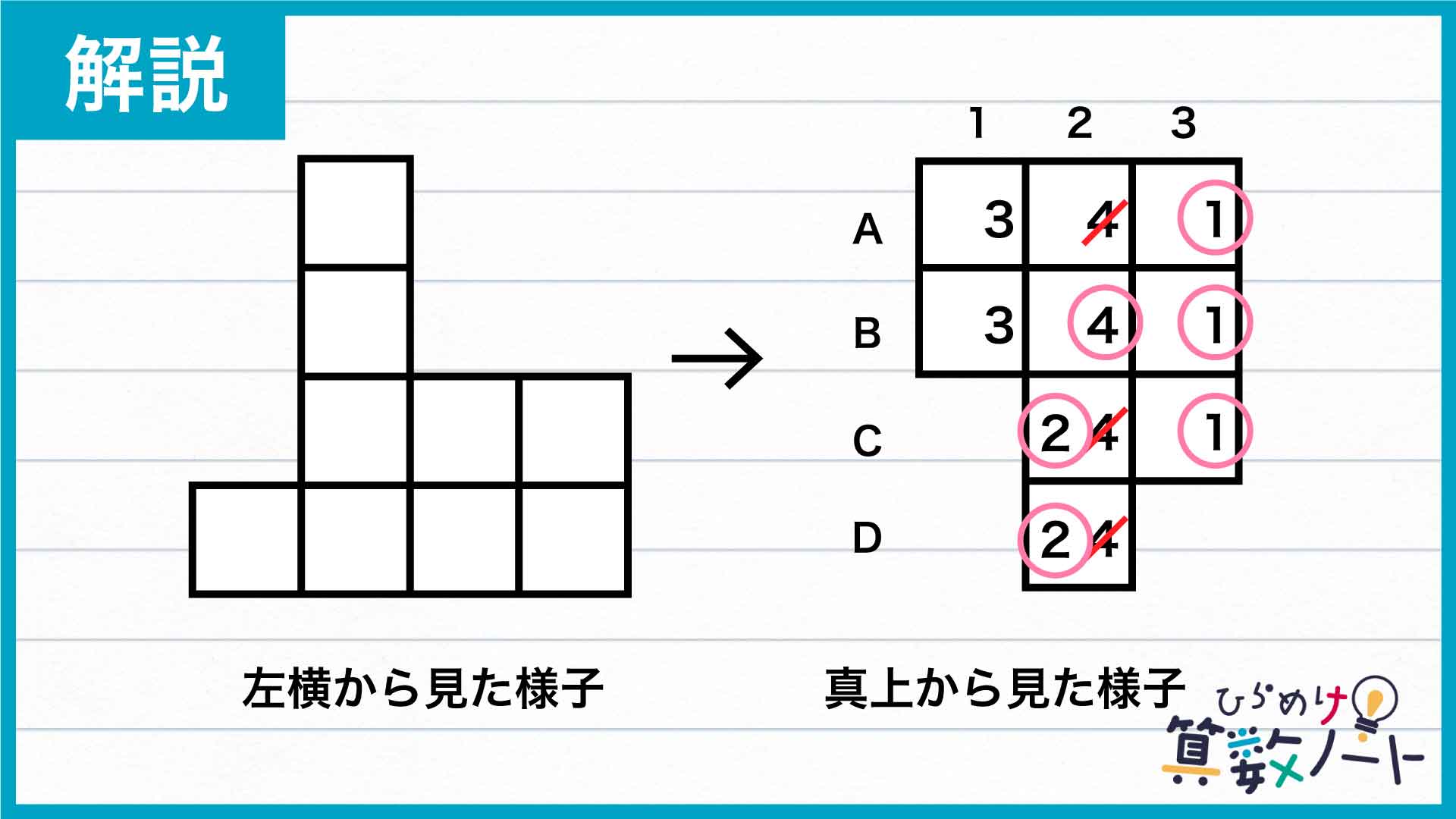
次に、真上から見た様子と左横から見た様子を照らし合わせます。
まず2の列について、Bの積み木が4個であることが確定し、さらにA、C、Dが4個である可能性はなくなることがわかります。またCの1とDの1には積み木がないこと、およびCの3の積み木は1個でDの3は積み木がない（3個以上積まれていると左横から見たときにはみ出して見えるはず）ことから、Cの2とDの2の積み木の数は2個であることが確定します。
また、Aの列は積み木が最も多くて1個しかないため、Aの1、Aの2、Aの3の積み木は全て1個となります。
したがって、どちらかが3個であるはずの1の列において、Aの1が3個ではないため、Bの1の積み木が3個であることが確定します。
数を整理する
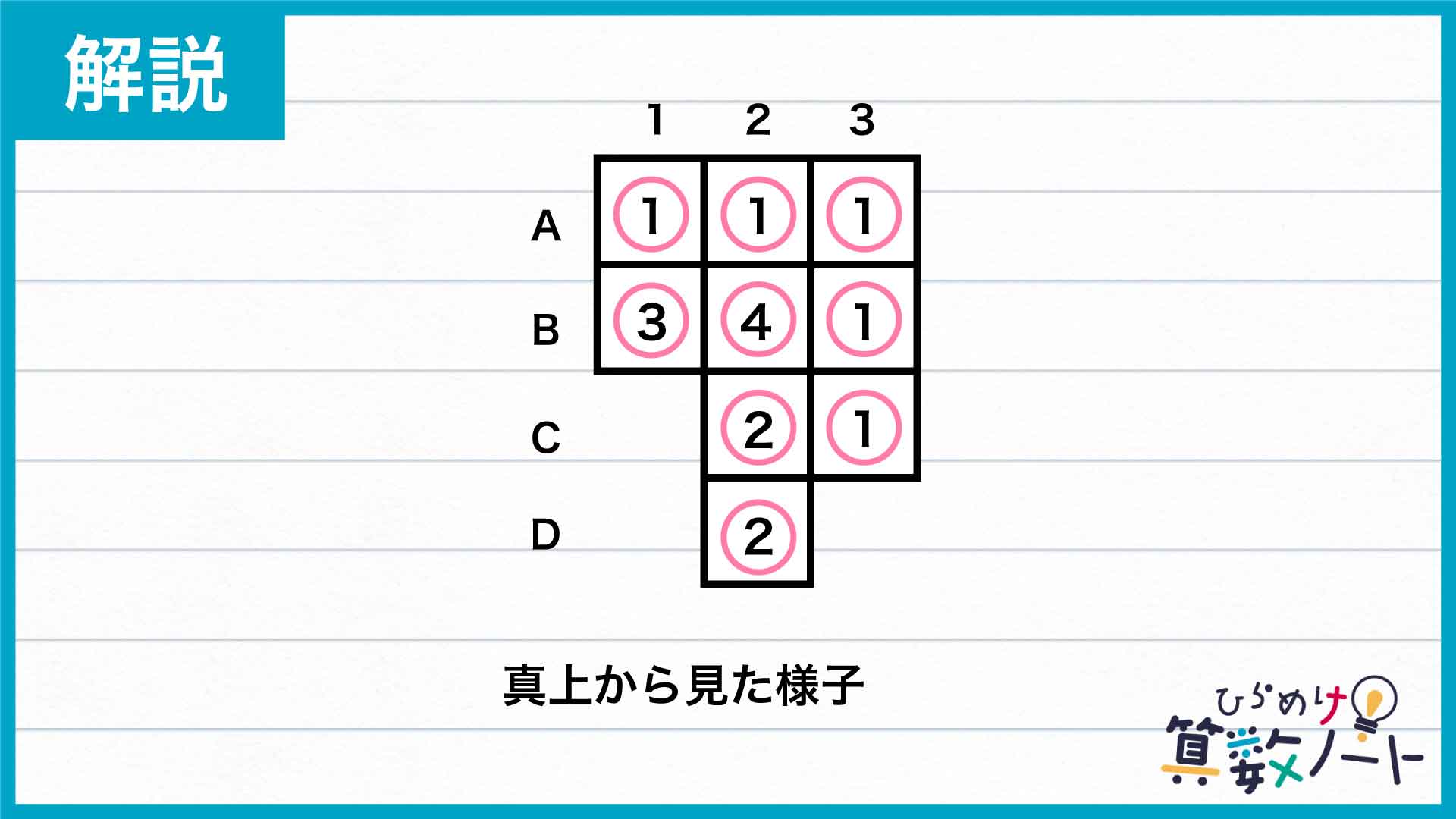
以上をまとめると、各場所の縦に積み重なった積み木の数は下の図のようになります。
したがって、すべての積み木の数は16個となります。
答え：16個
それではまた次の算数ノートでお会いしましょう！
「ひらめけ！算数ノート」のバックナンバーはこちらから！
【前回の算数ノートはこちら】
【あわせて読みたい】
