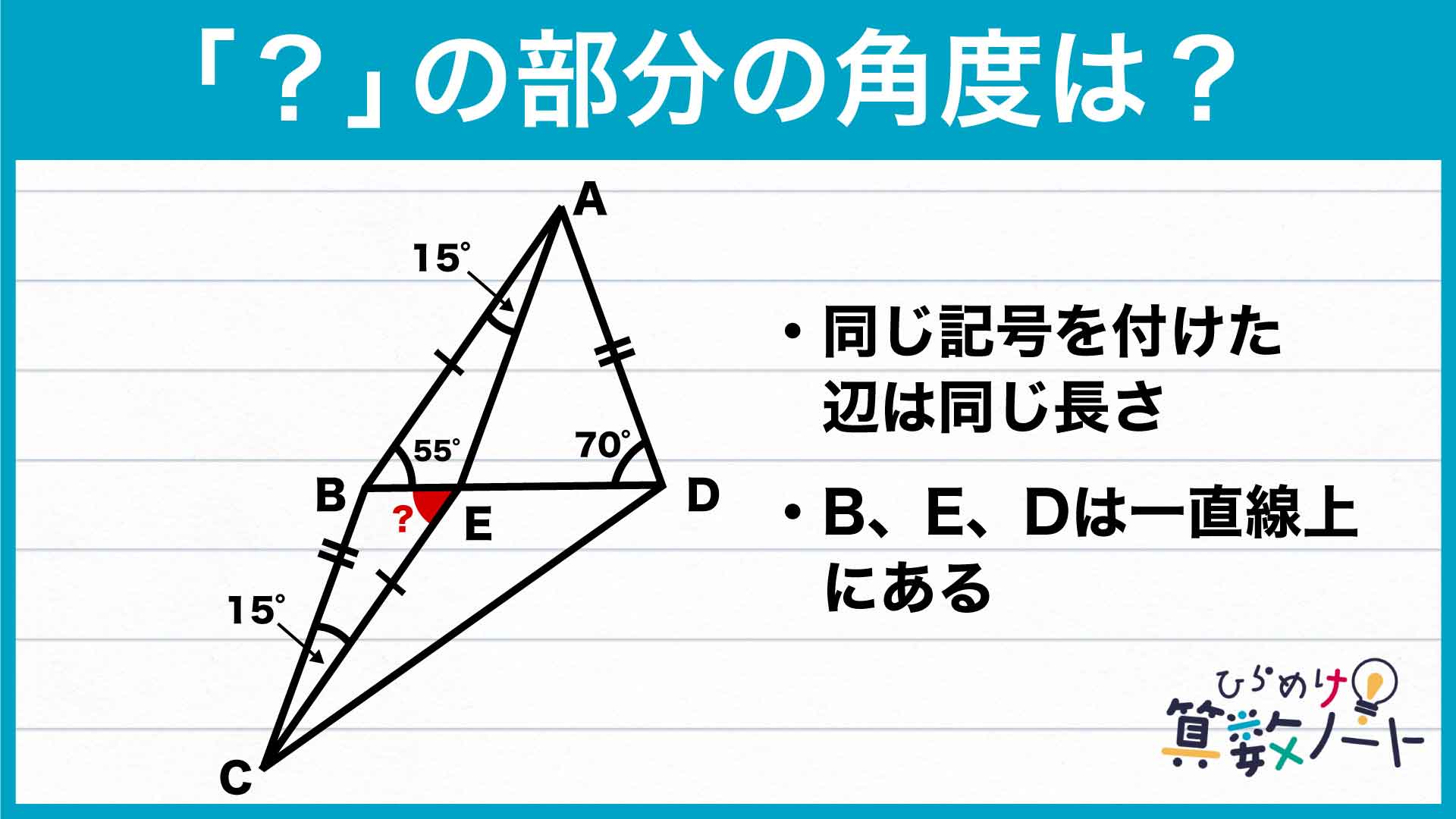
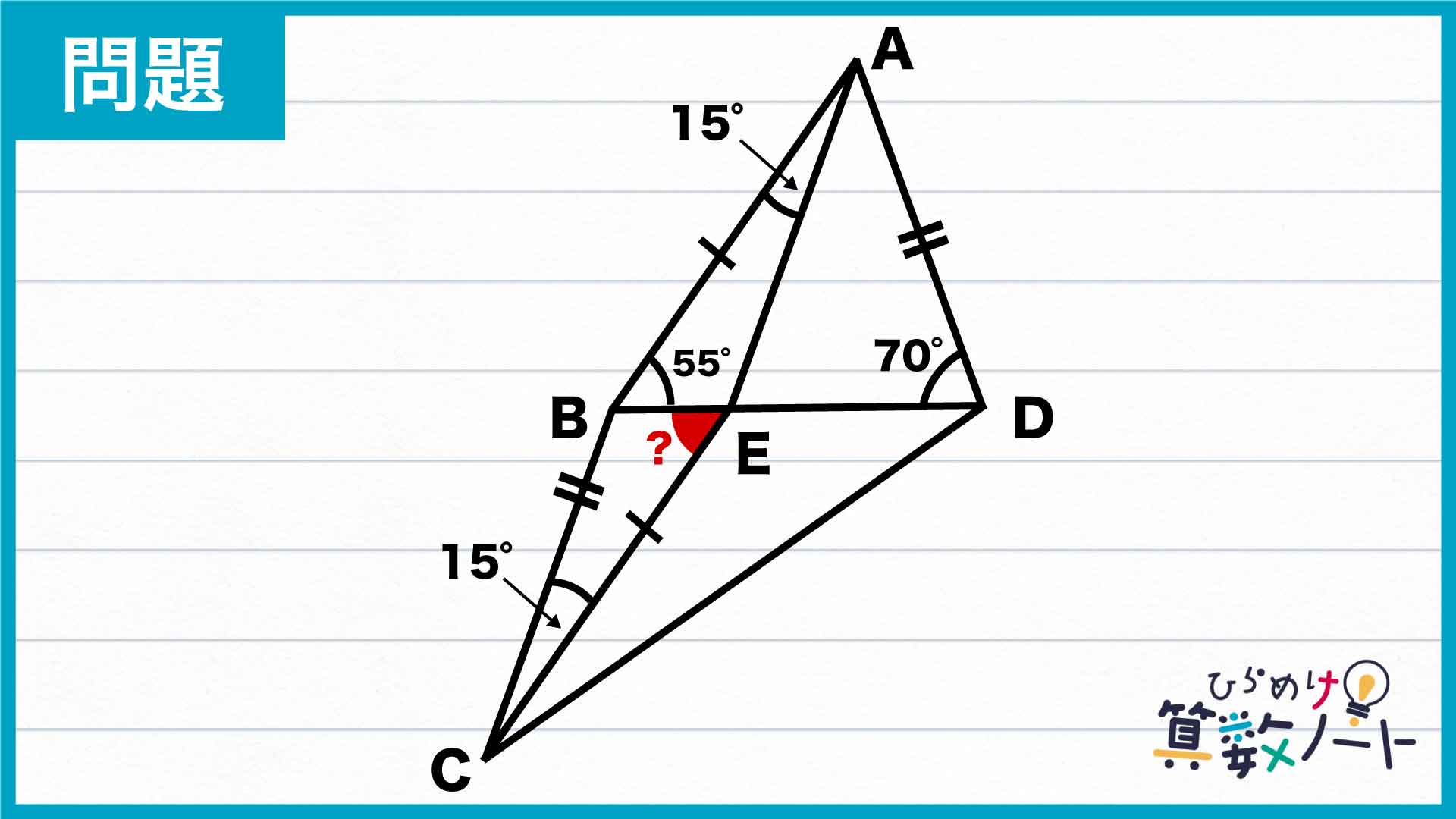
問題はこちら
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
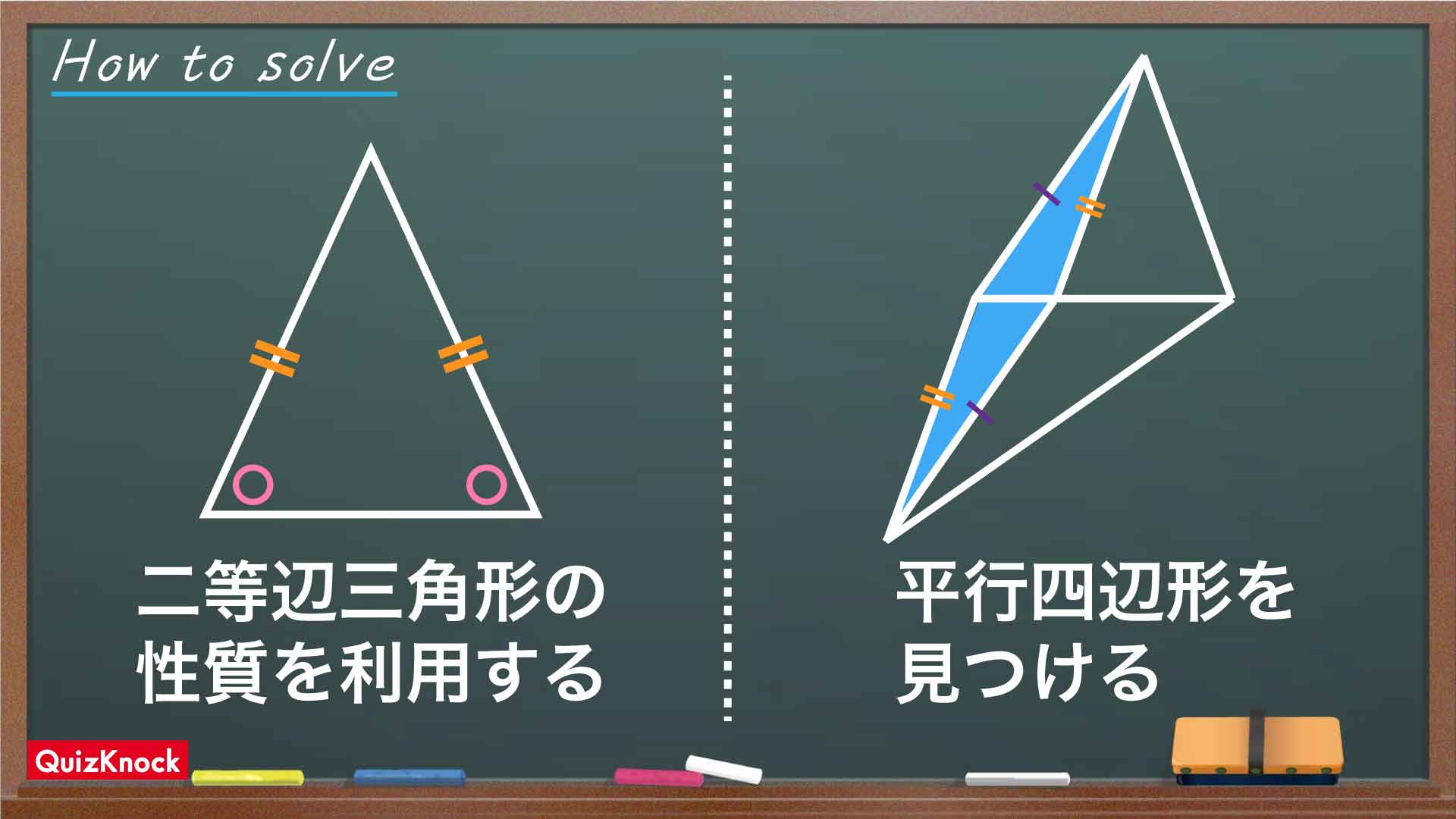
今回の問題を解くうえで重要なポイントは、以下の2つです。
これらのポイントを踏まえながら、問題を解いていきましょう。
二等辺三角形の性質を利用する
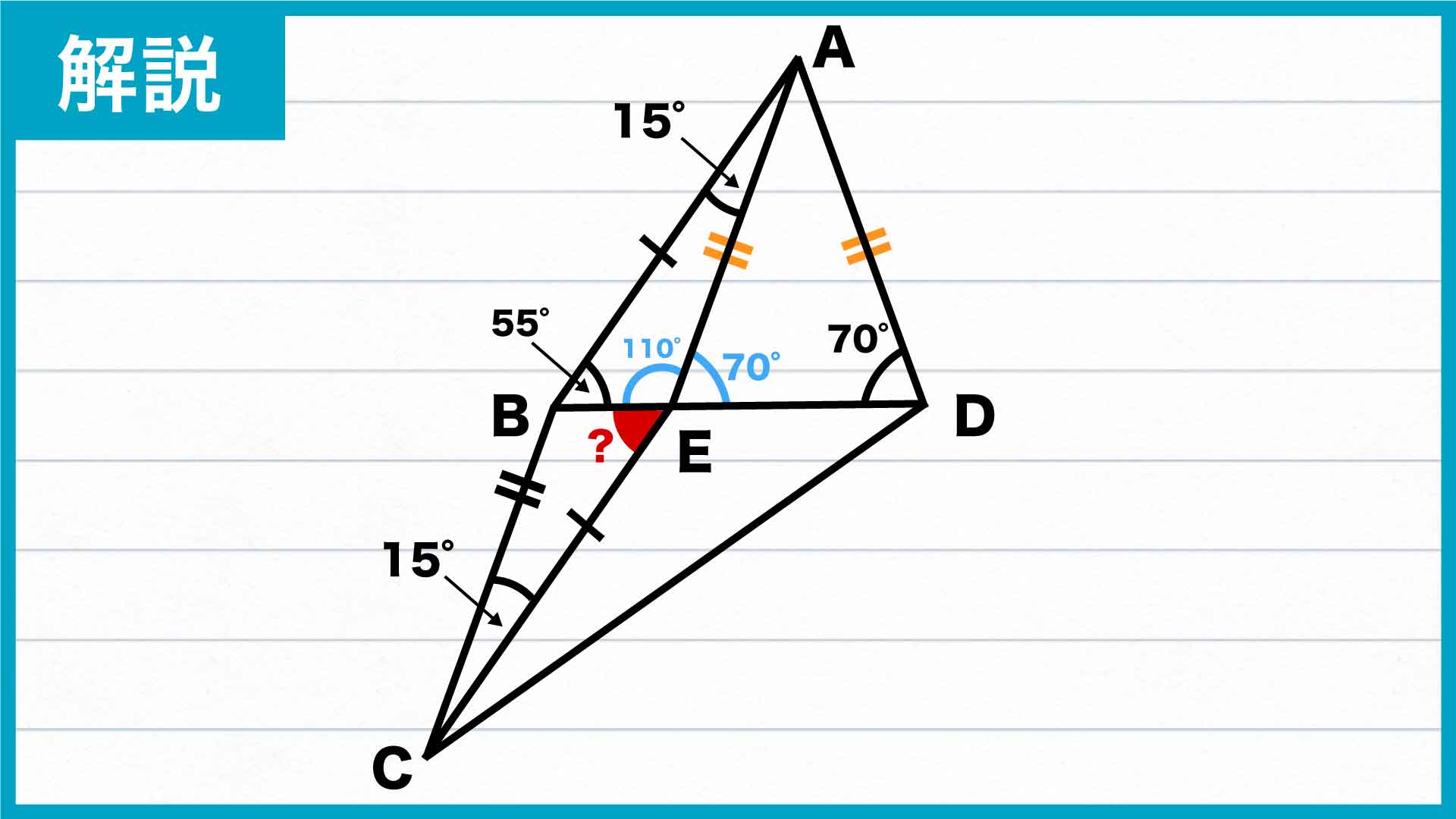
角AEBの大きさは、180-（角ABE+角BAE）=110度ですから、角AEDの大きさは180-110=70度です。したがって、三角形ADEは角ADE=角AEDの二等辺三角形になります。
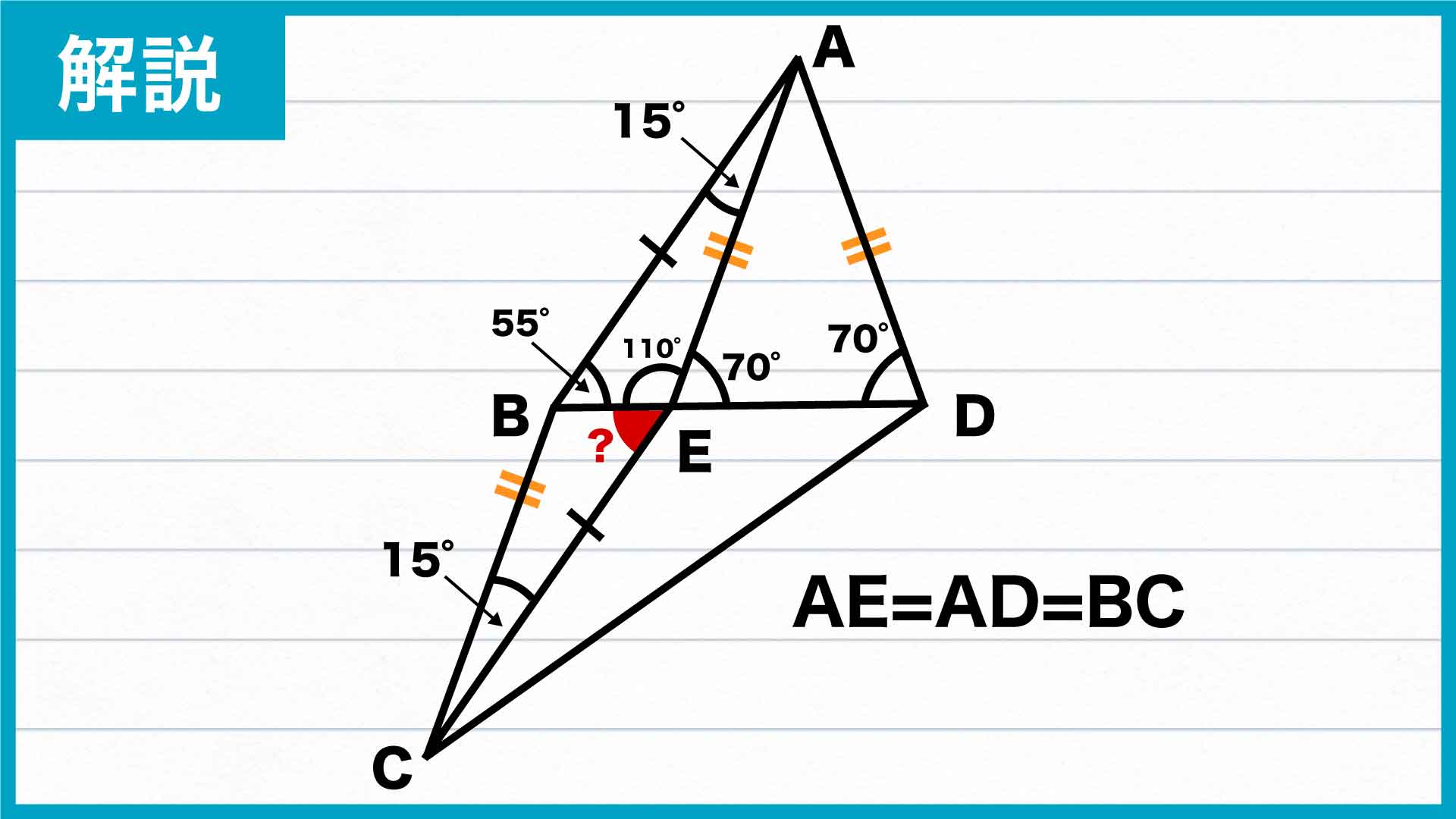
二等辺三角形の性質から辺ADと辺AEの長さは等しくなります。さらに、与えられた条件からBCとADの長さも等しいので、AE=AD=BCとなります。
平行四辺形を見つける
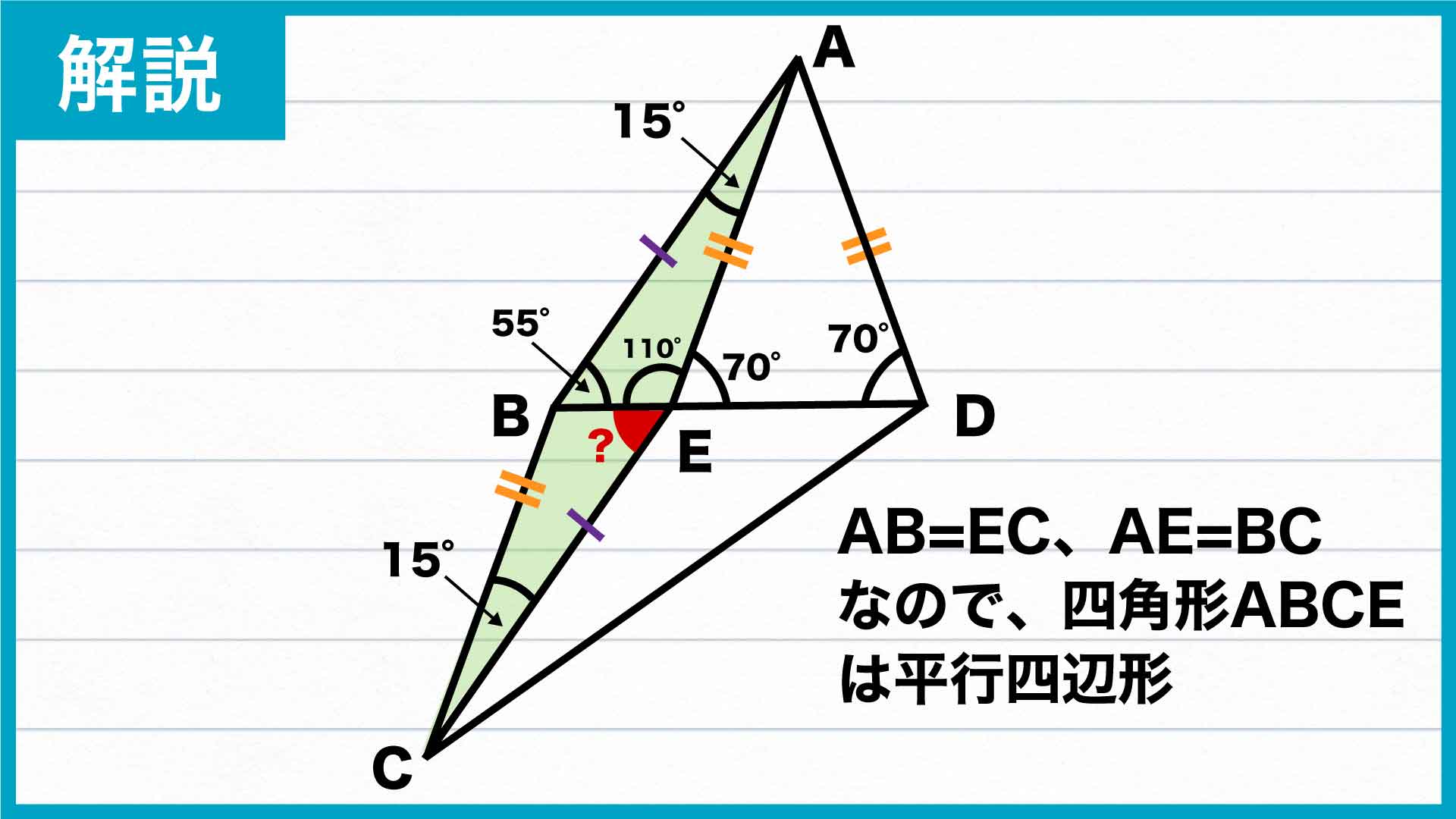
続いて、四角形ABCEに着目します。先ほど示したAE=BC、及び問題の条件であるAB=ECからであることふまえると、四角形ABCEは「向かい合う辺の長さがそれぞれ等しい」ことから平行四辺形であることがわかります。
平行四辺形の性質を使って角度を求める
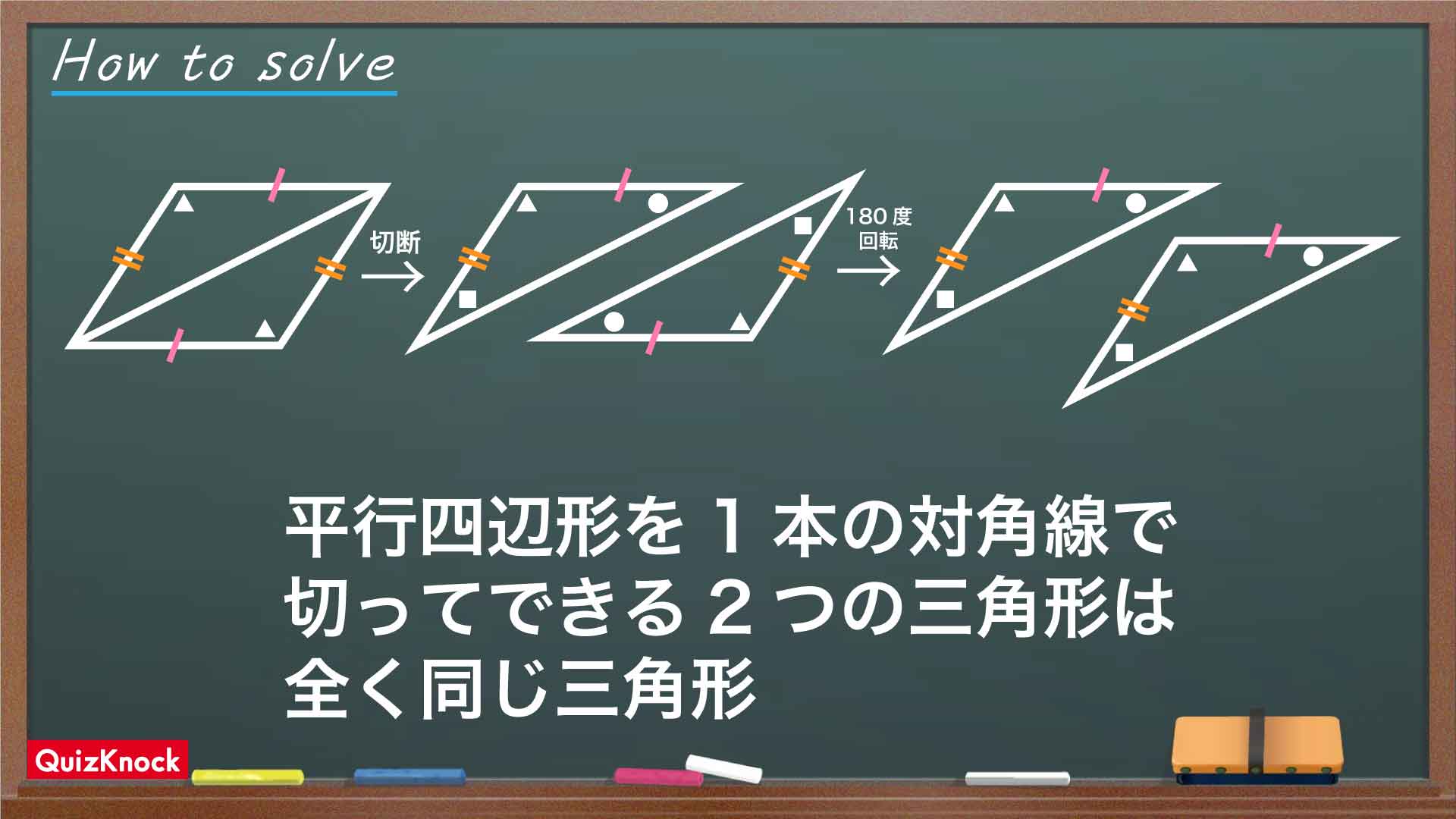
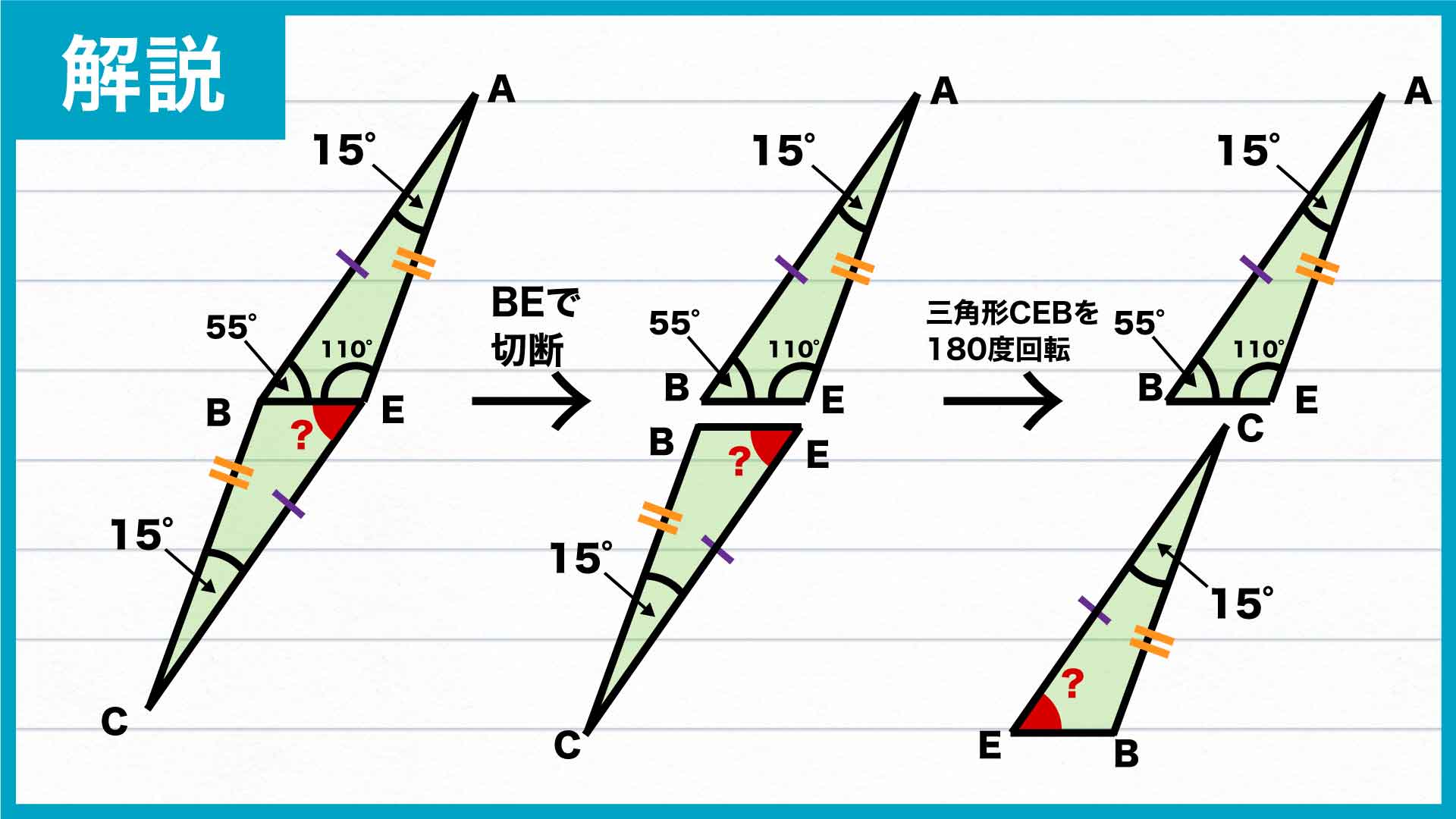
平行四辺形の性質として、1本の対角線で切ってできる2つの三角形は全く同じ図形になります。
線分BEは平行四辺形ABCEの対角線なので、BEによって分けられた2つの三角形ABEとCEBは全く同じ三角形になります。
したがって、求める角CEBの大きさは角ABEの大きさと同じく、55度となります。
答え：55度
「ひらめけ！算数ノート」のバックナンバーはこちら！
【前回の算数ノートはこちら】
【あわせて読みたい】
