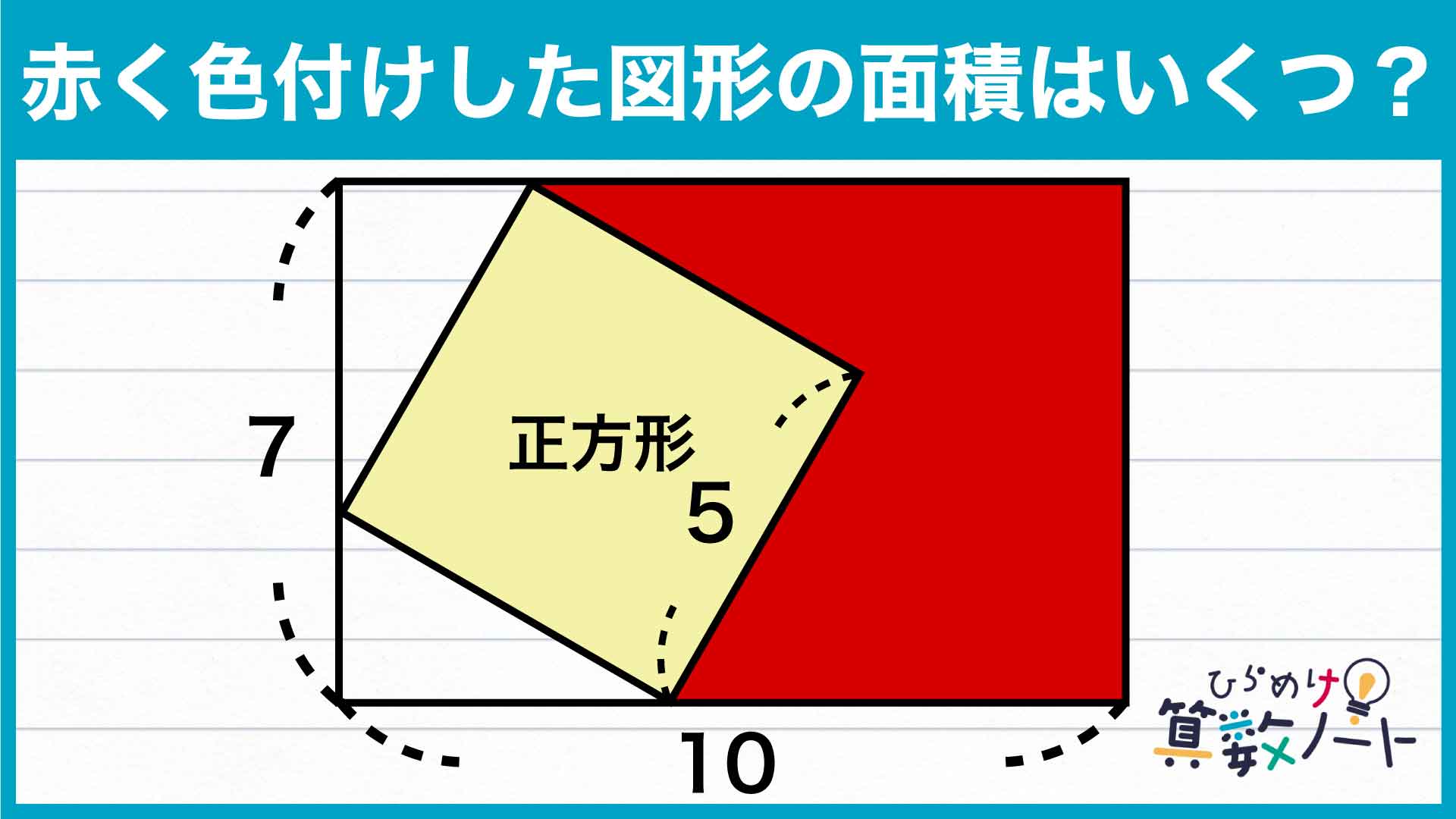
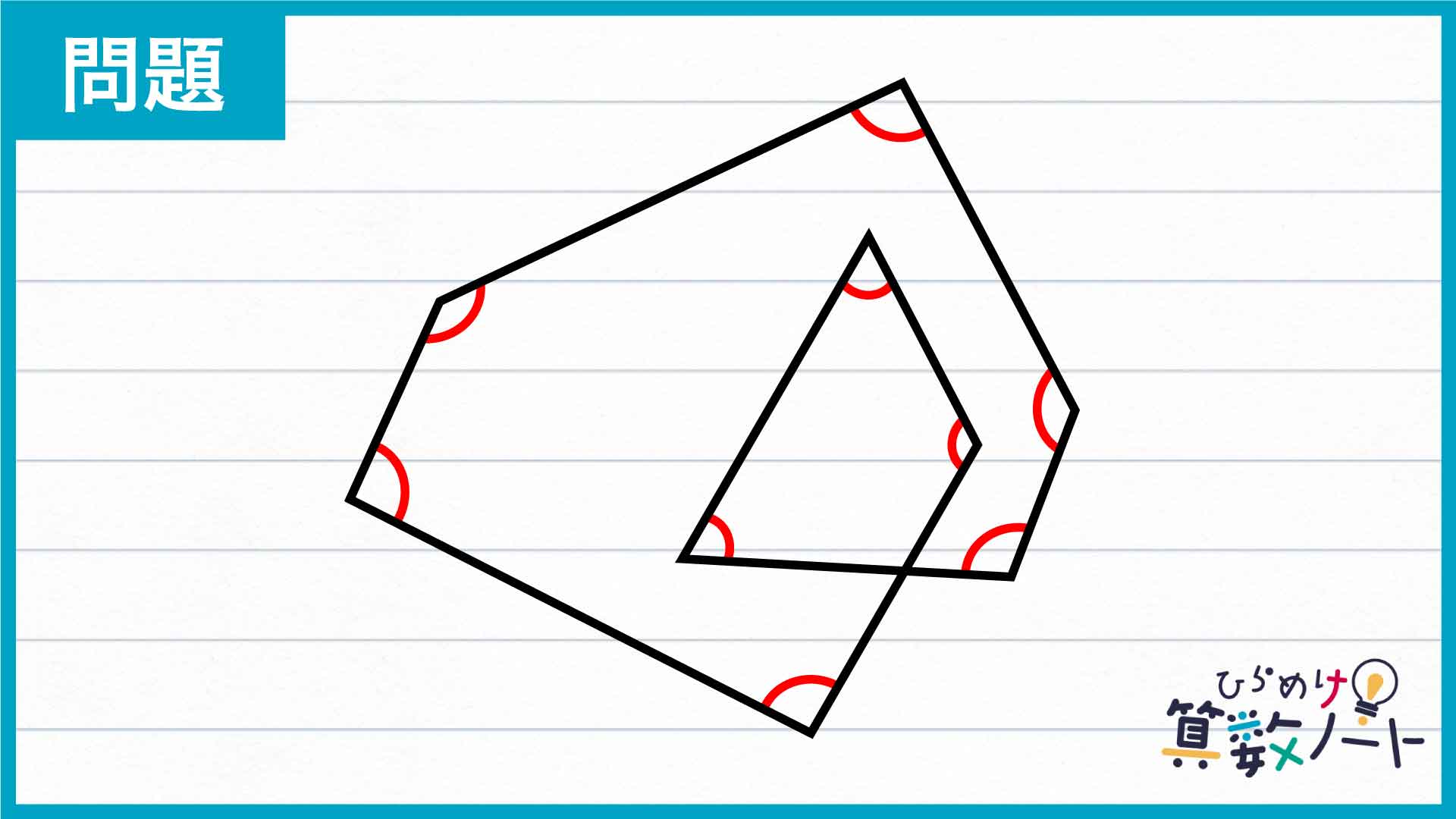
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
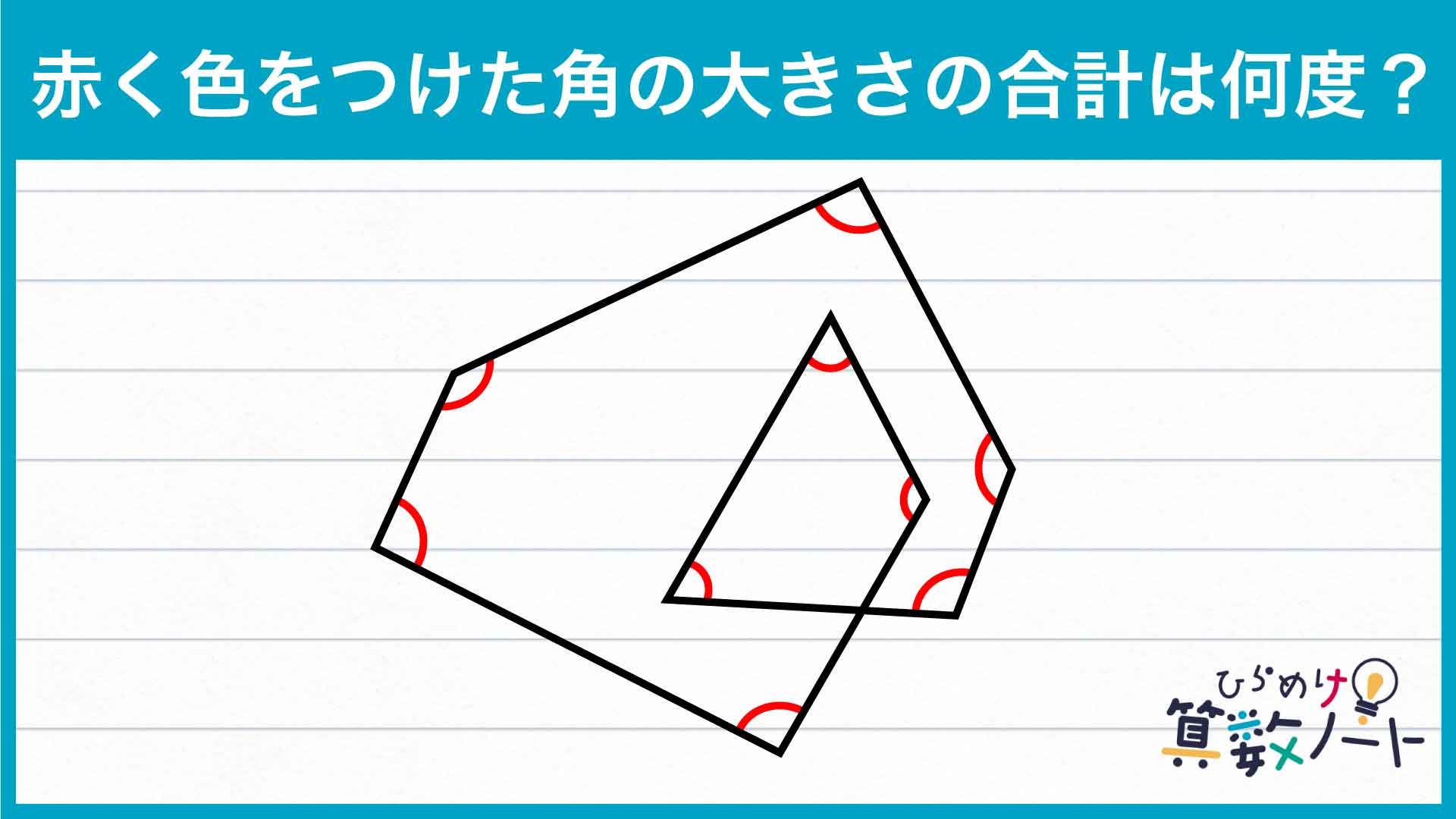
解説
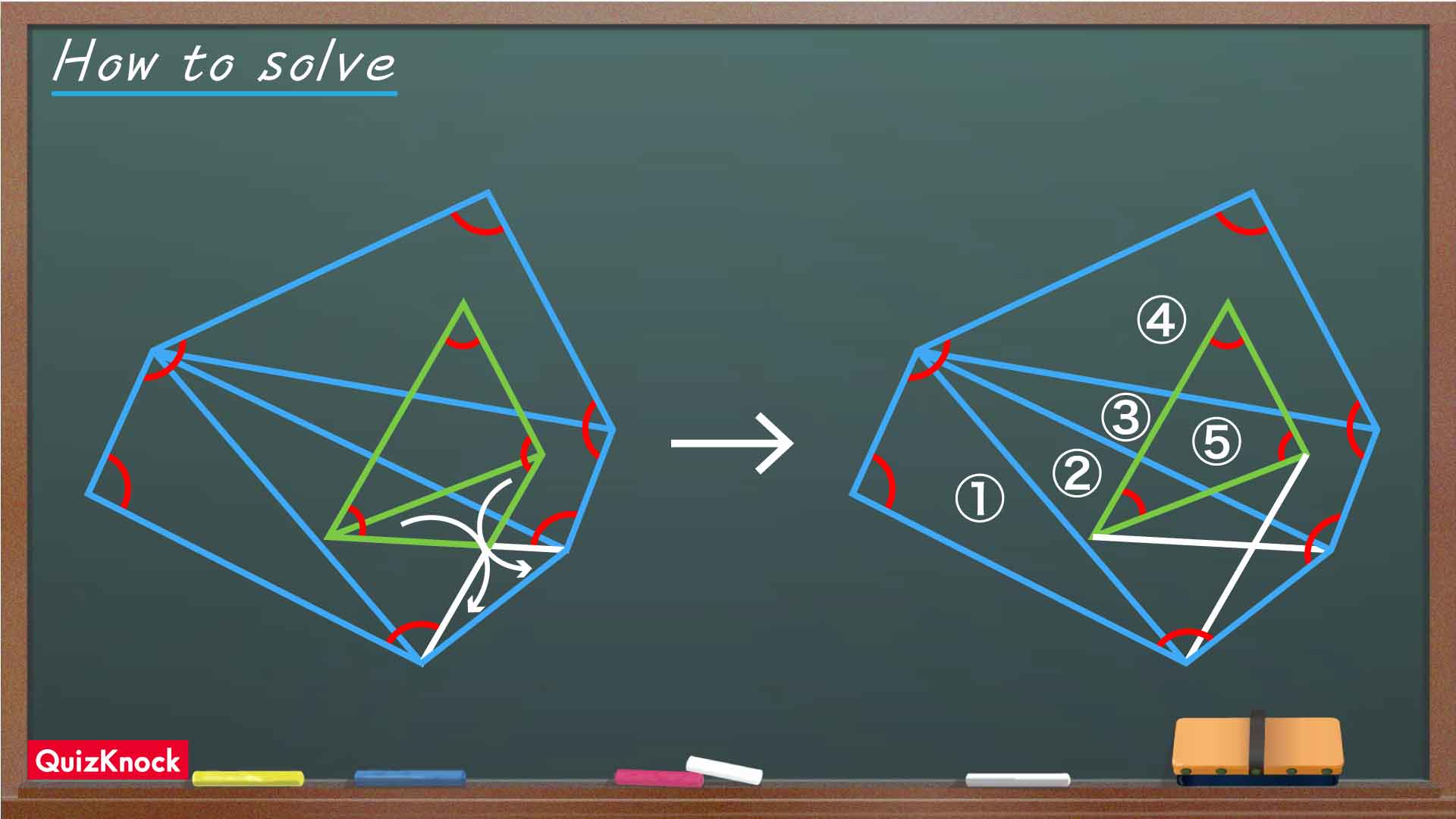
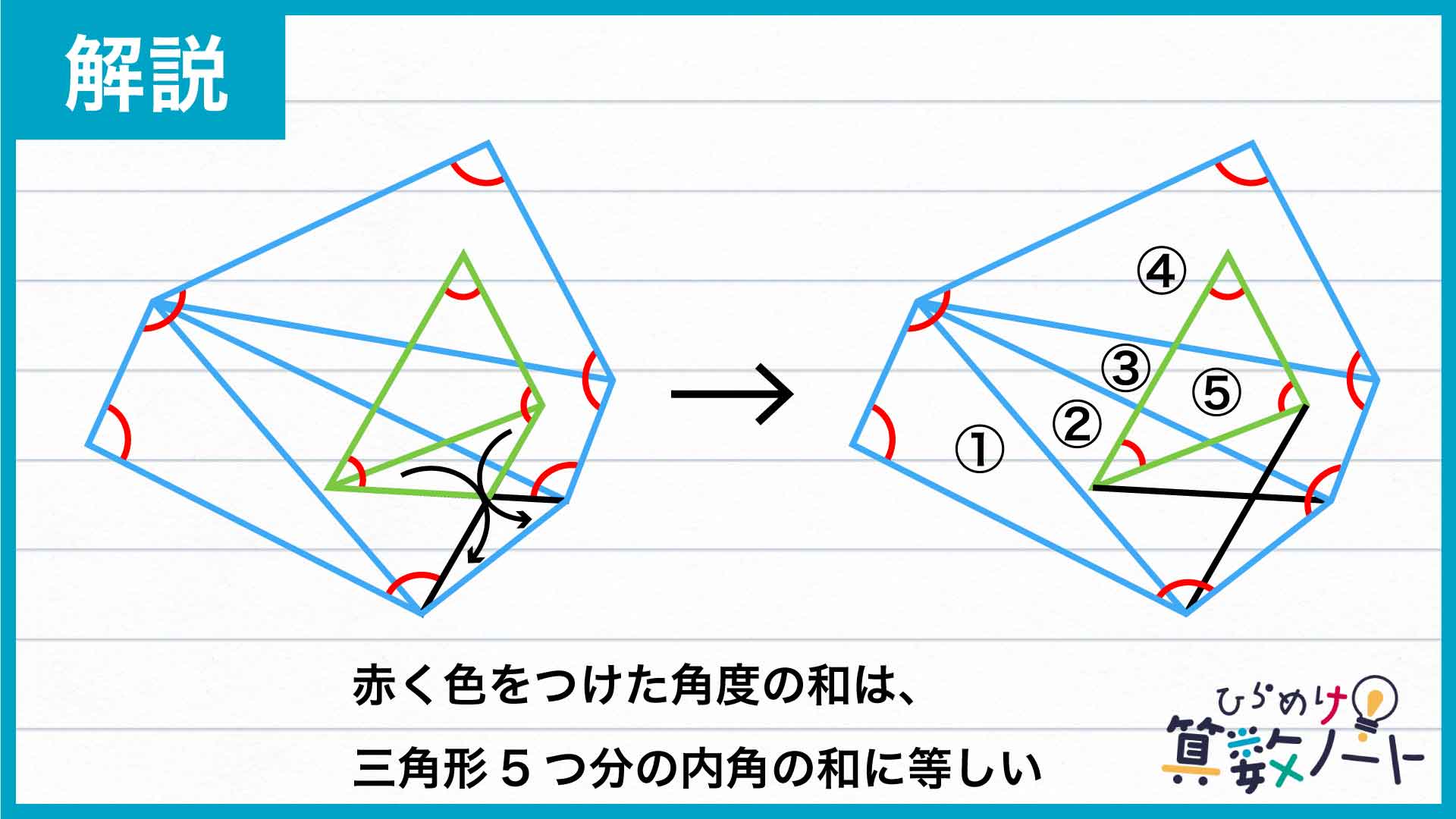
今回の解き方をまとめた図がこちらです。
補助線を引き図形を分割して、求める角度を三角形の内角で表すことがポイントです。
では、このポイントを踏まえて解いていきましょう!
補助線を引いて図形を三角形に分割する
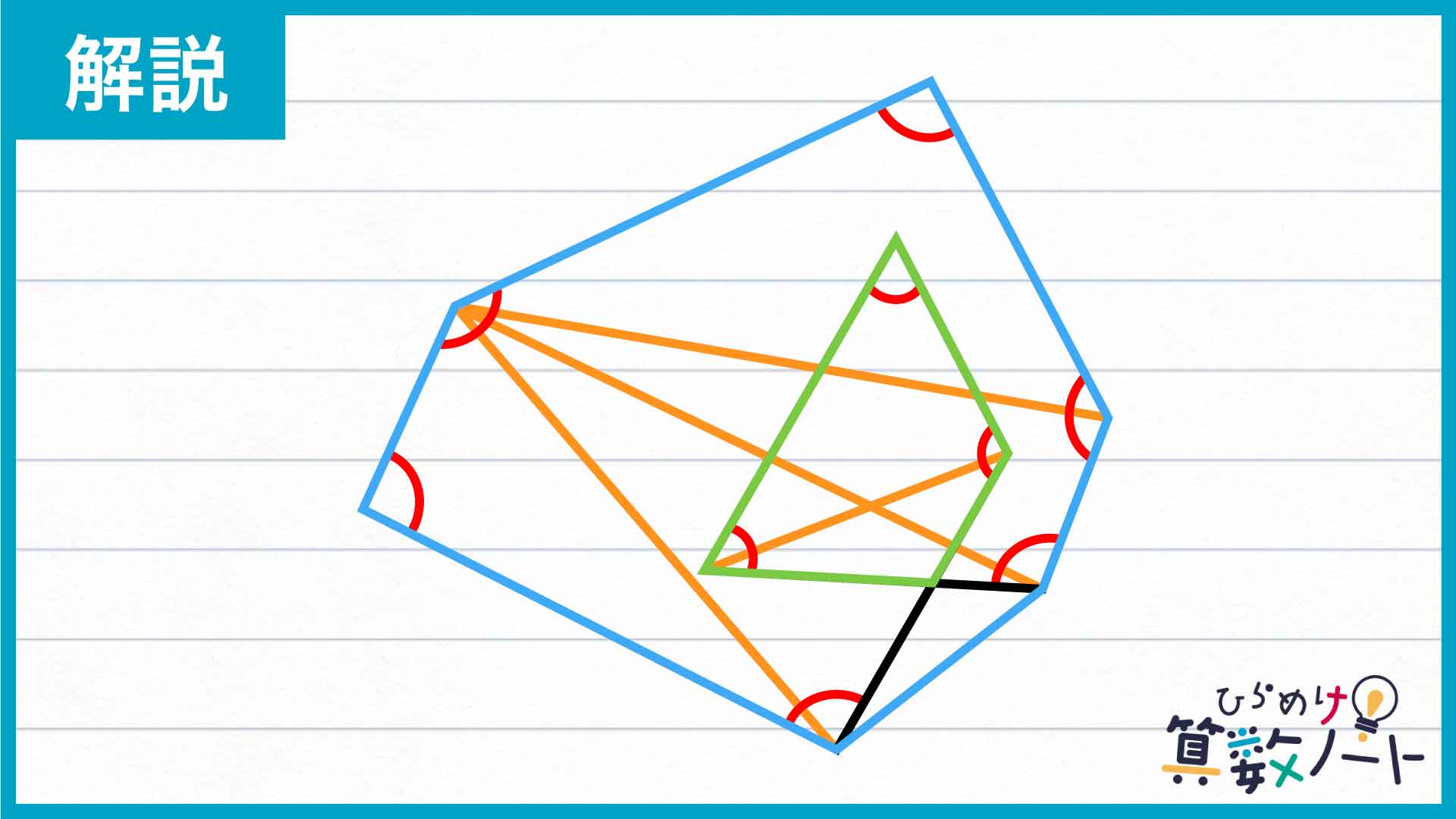
まず、下の図のように補助線を引いて、三角形をたくさん作ります。青く色をつけた七角形は4つ、緑色に色をつけた四角形は2つの三角形に分割でき、赤い印をつけた角のほとんどを三角形の内角にすることができました。
三角形の内角の和が180度であることを利用して角度の合計を計算したいところですが、下の図でオレンジ色をつけた角はそれを利用できない状態であるため、このままでは答えを出せません。
「砂時計の形」に着目して角度を移動する
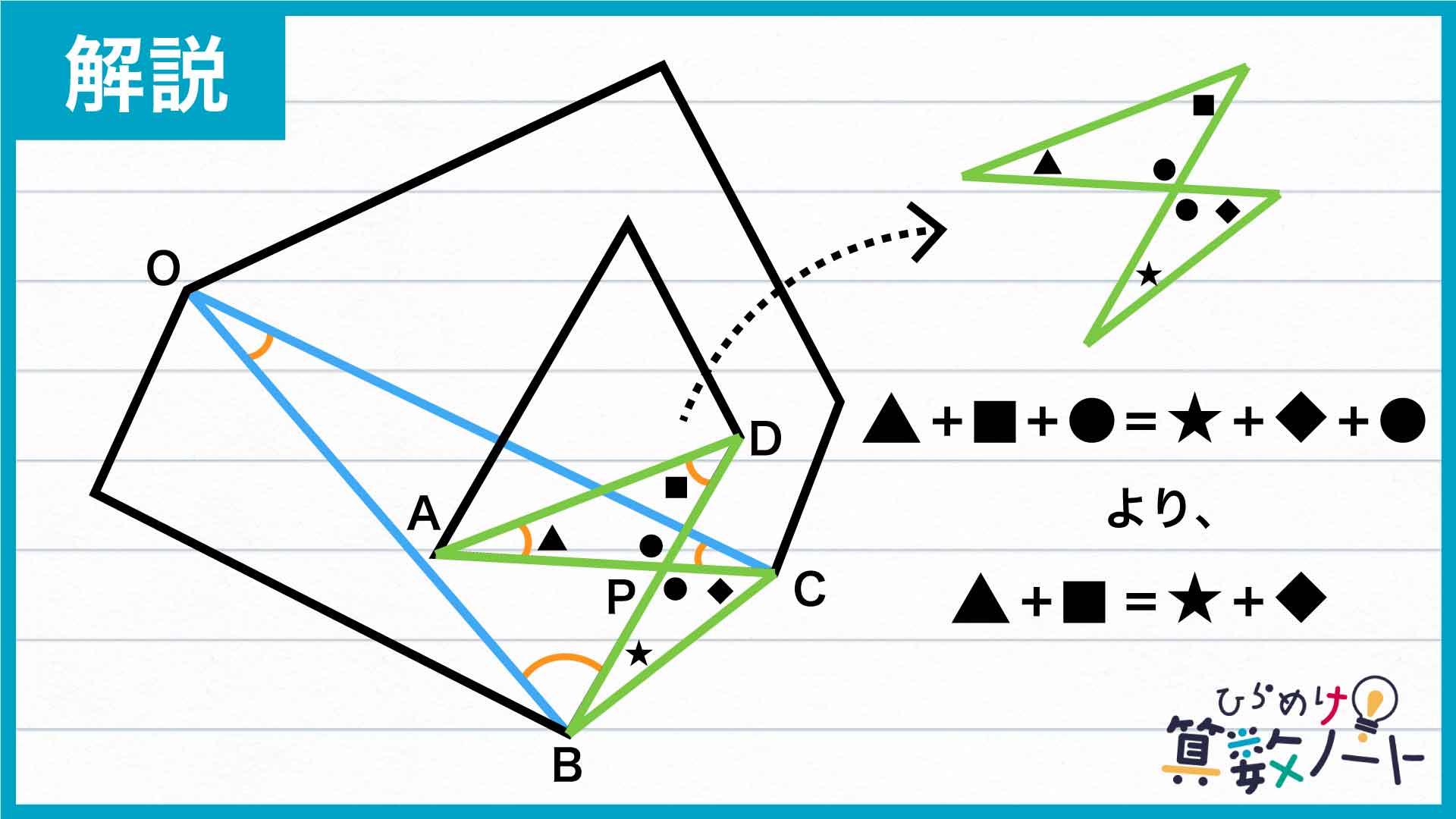
下の図で、2つの緑色の三角形が向かい合って砂時計のような形になっている部分に着目します。この2つの三角形は対頂角(向かい合う角)の大きさが等しいため、それぞれの三角形の残りの2つの角度の和は等しくなります。
三角形APDと三角形CPBの内角の大きさに着目すると、▲+■+●=★+◆+●=180度であることから、▲+■=★+◆が成り立つのです。
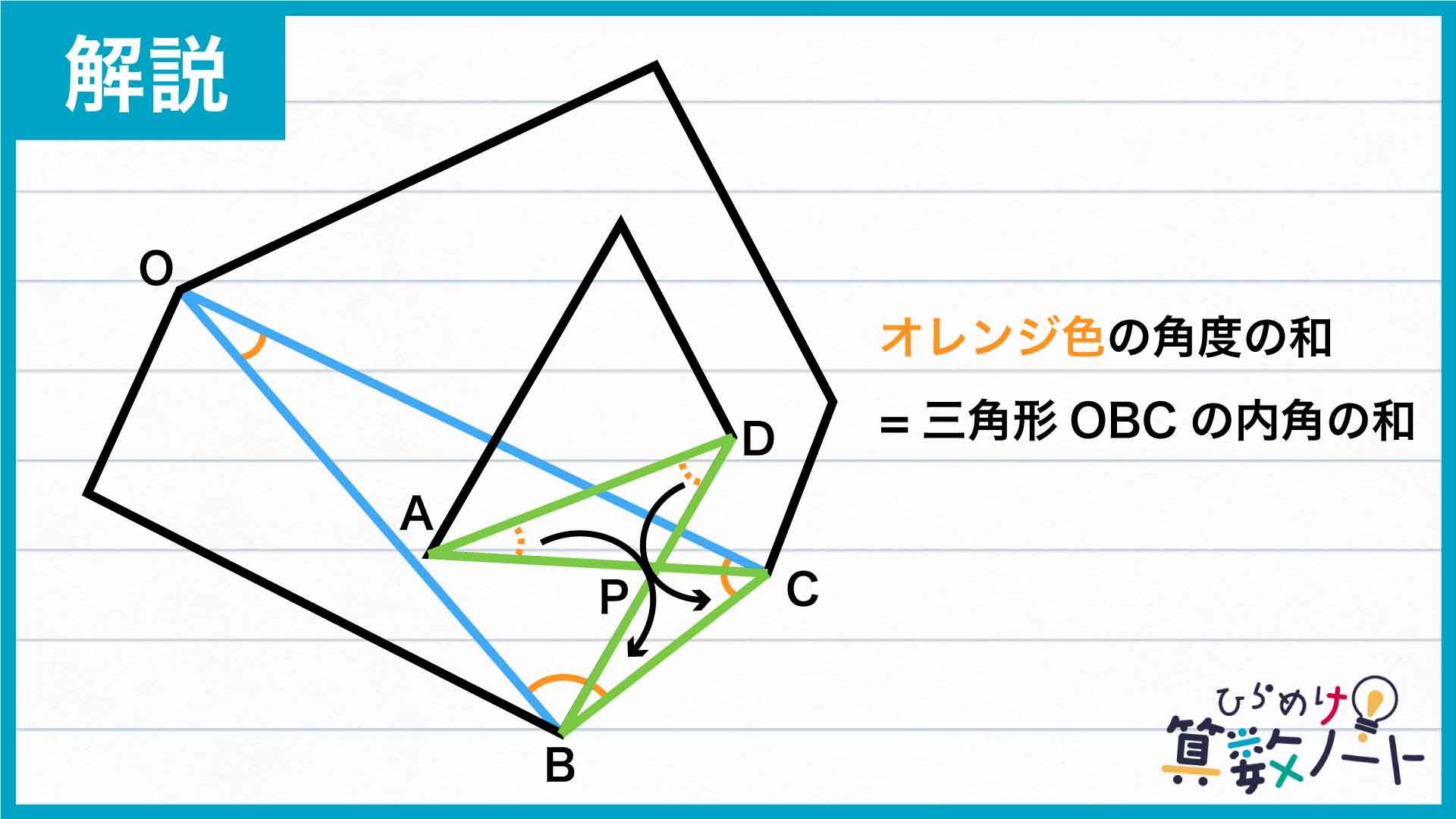
つまり、オレンジ色をつけた角度の和は三角形OBCの内角の和に等しく、180度と求まります。
求める角度は、180度が何個分?
以上を整理すると、求める角度の合計は三角形5個分の内角の総和と等しく、180×5=900度と求まります。
答え:900度
およそ1年前に出題したこちらの問題も、同じように考えることが発想の糸口になっています。ぜひもう一度挑戦してみてくださいね。
それでは、また次の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)