小学生でも解ける「四角形の面積」の問題に挑戦！あなたは解ける？

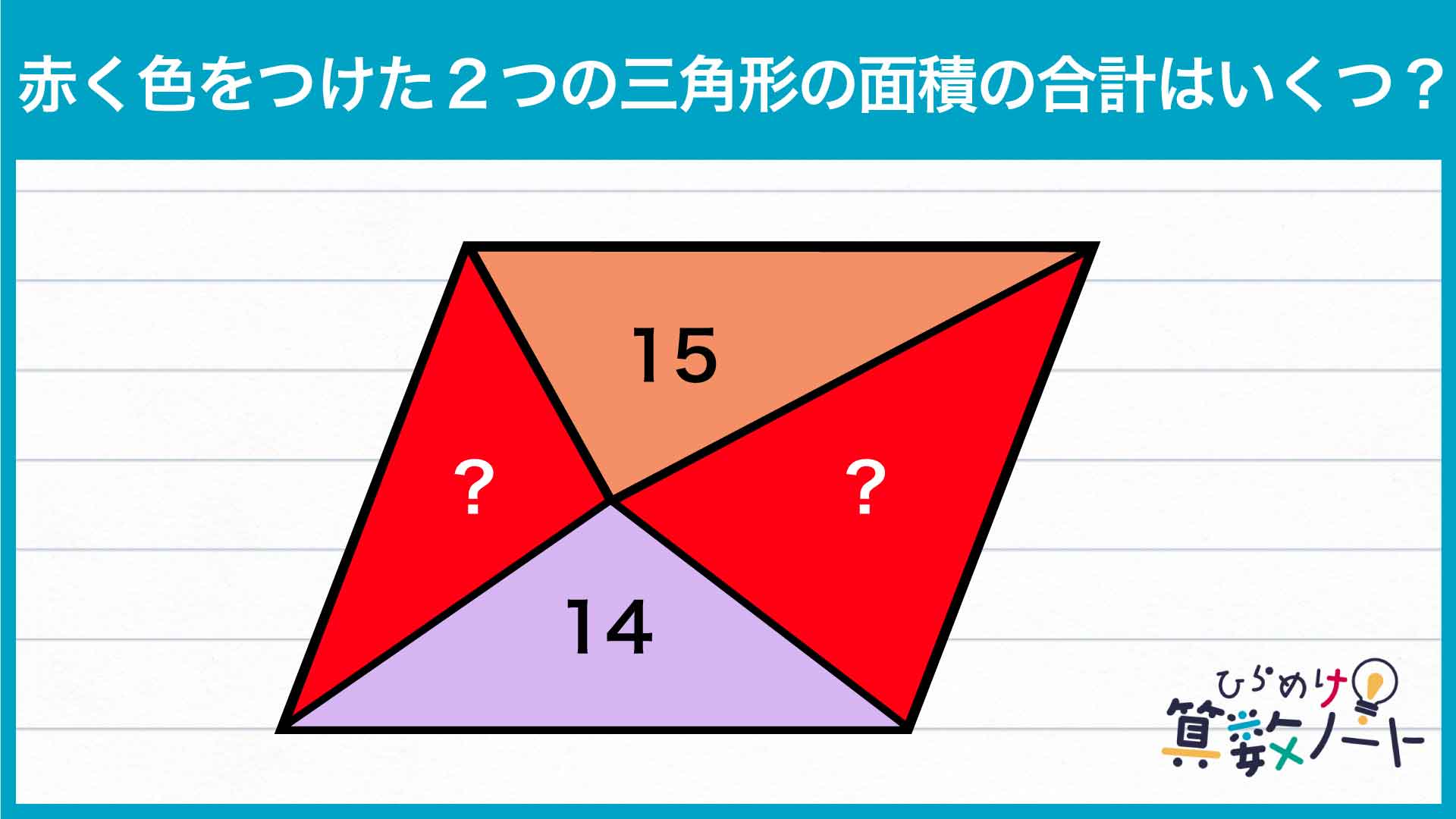
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：自力で解きたい方はこちらへ！以下は問題の解説です

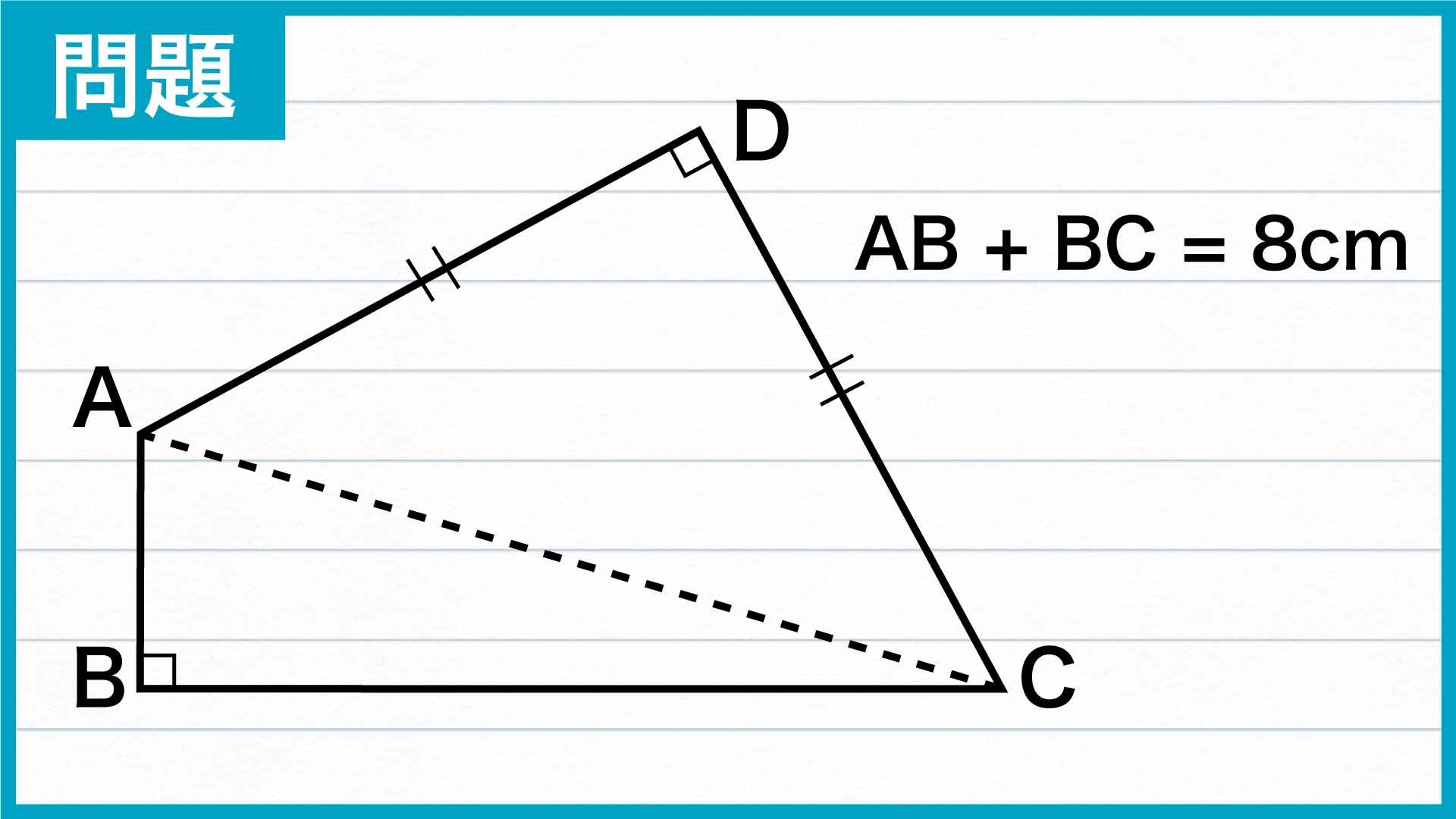
今回の問題を解くうえで重要なポイントを以下にまとめました。

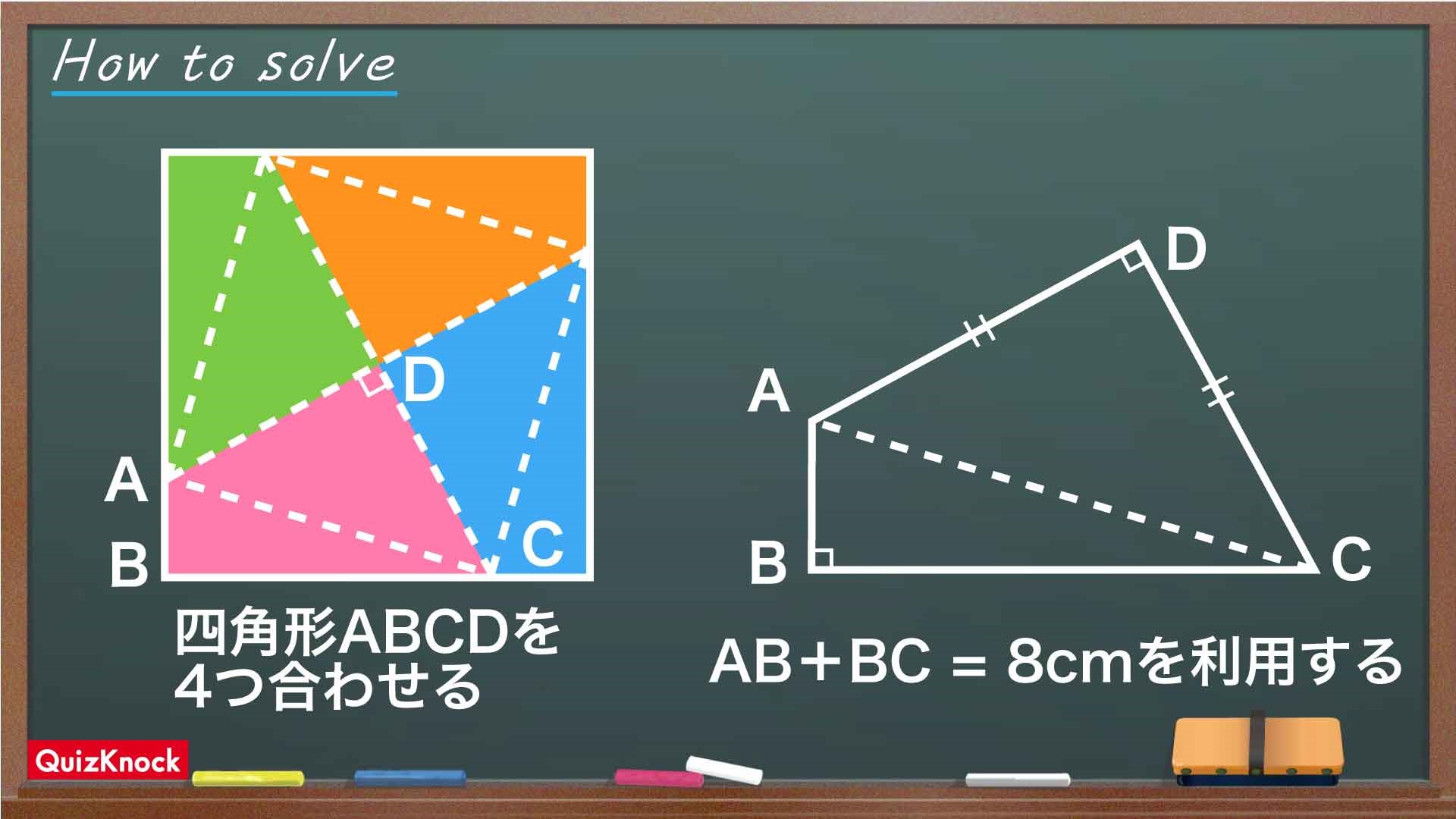
整理すると、

• 四角形ABCDを4つ合わせて正方形をつくる。
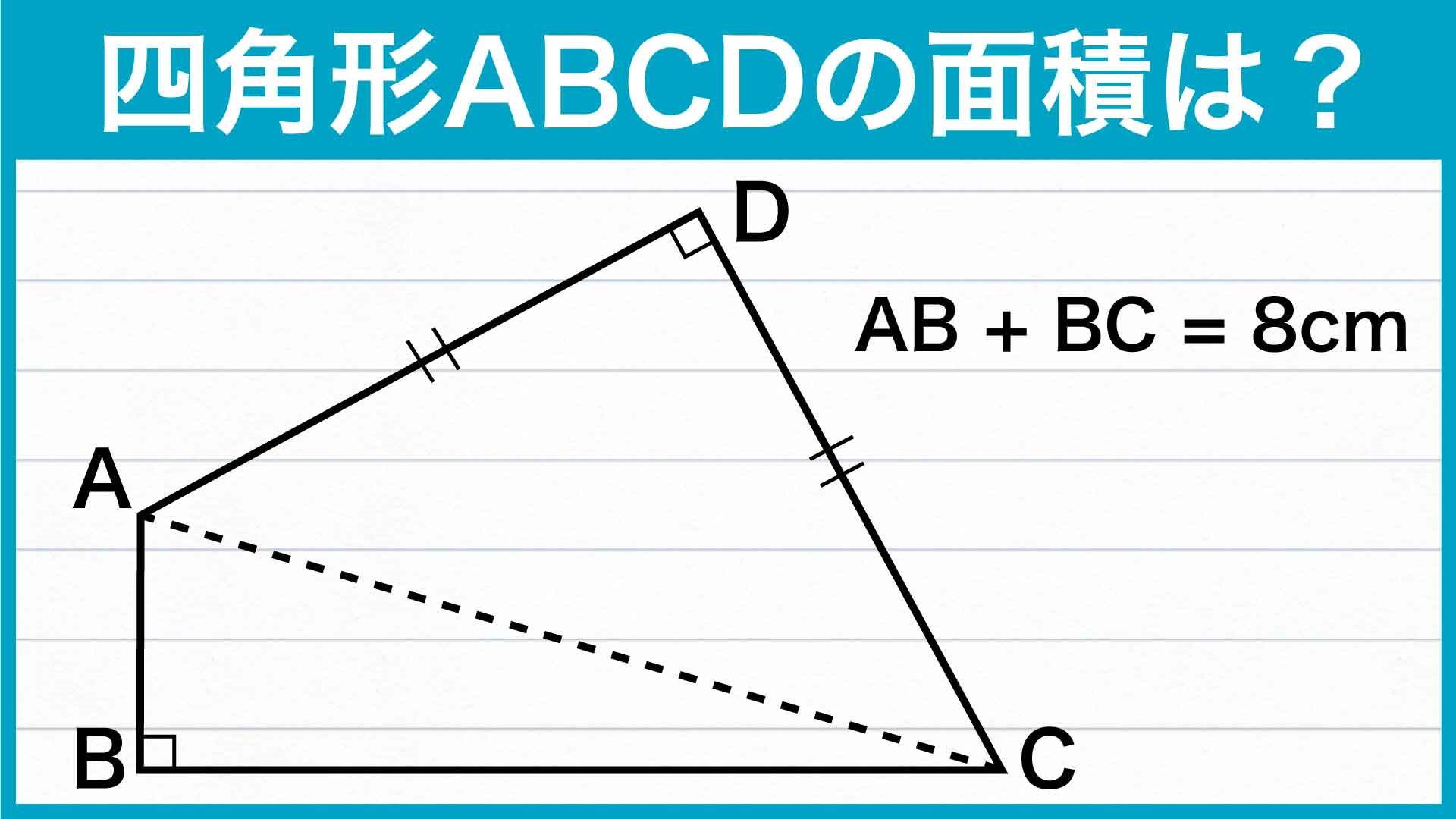
• ABとBCの長さの和が8cmであることを利用する。

の2点です。これらのポイントを踏まえて、問題を解いていきましょう。

四角形ABCDを合わせて正方形を作る

ADとCDの長さが等しいこと、また角ADCが直角であることから、ADとCDの部分をつなげることで、四角形ABCDをぴったり4つ合わせることができます。さらに、角BAD＋角BCD=180°であることから、隣り合う2つの四角形は一直線上に並ぶため、四角形ABCDを4つ合わせてできる図形はちょうど四角形になることがわかります。ここで、できあがった図形を「大きな四角形」と呼ぶことにします。

この「大きな四角形」のそれぞれの辺の長さは、「ABの長さとBCの長さの和」で全て同じなので、「大きな四角形」は正方形であることがわかります。

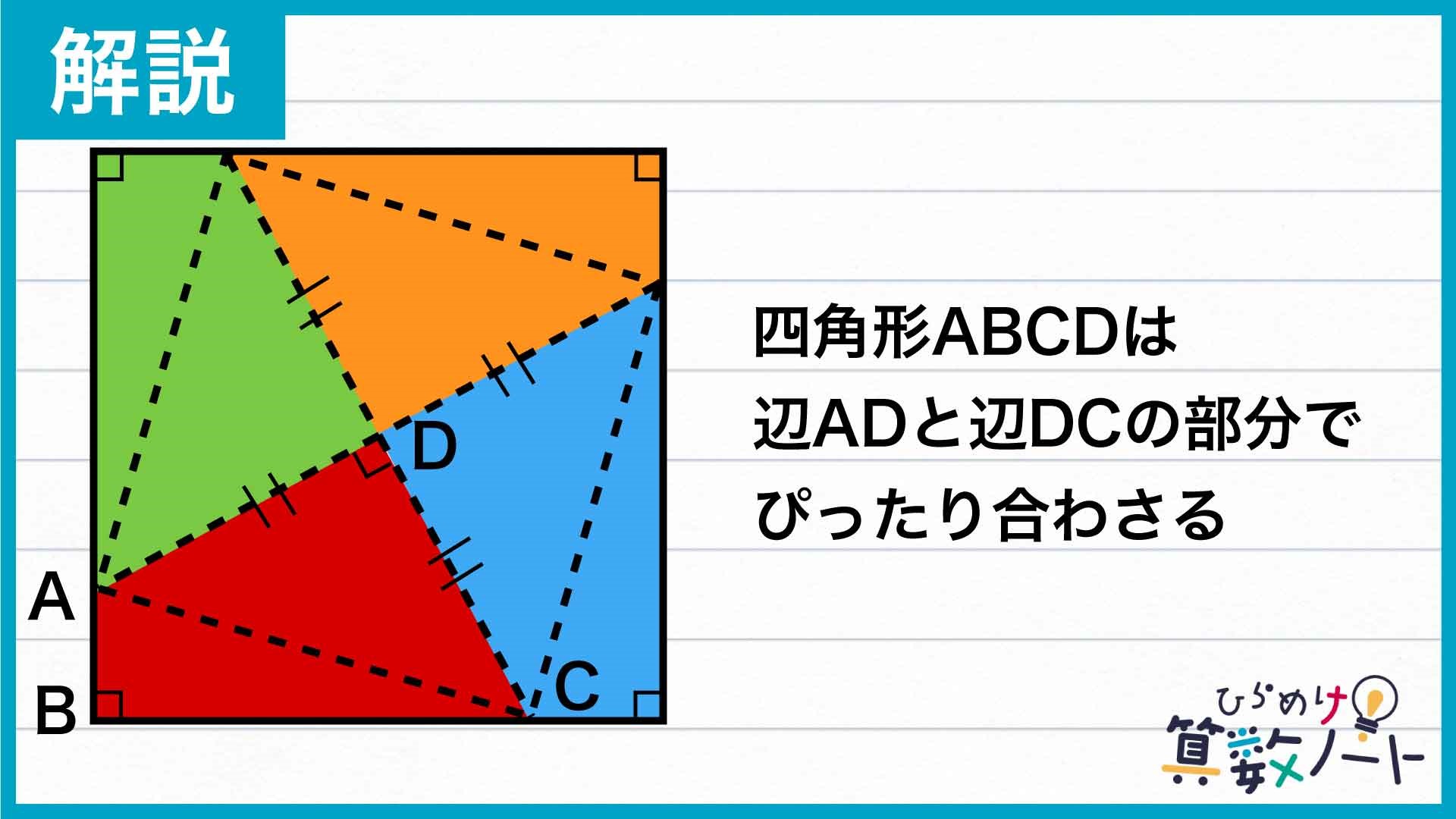
完成した正方形の面積から四角形ABCDの面積を求める

正方形の一辺の長さは、問題文から（ABの長さ）+（BCの長さ）=8cmなので、正方形の面積は8×8=64cm²となります。

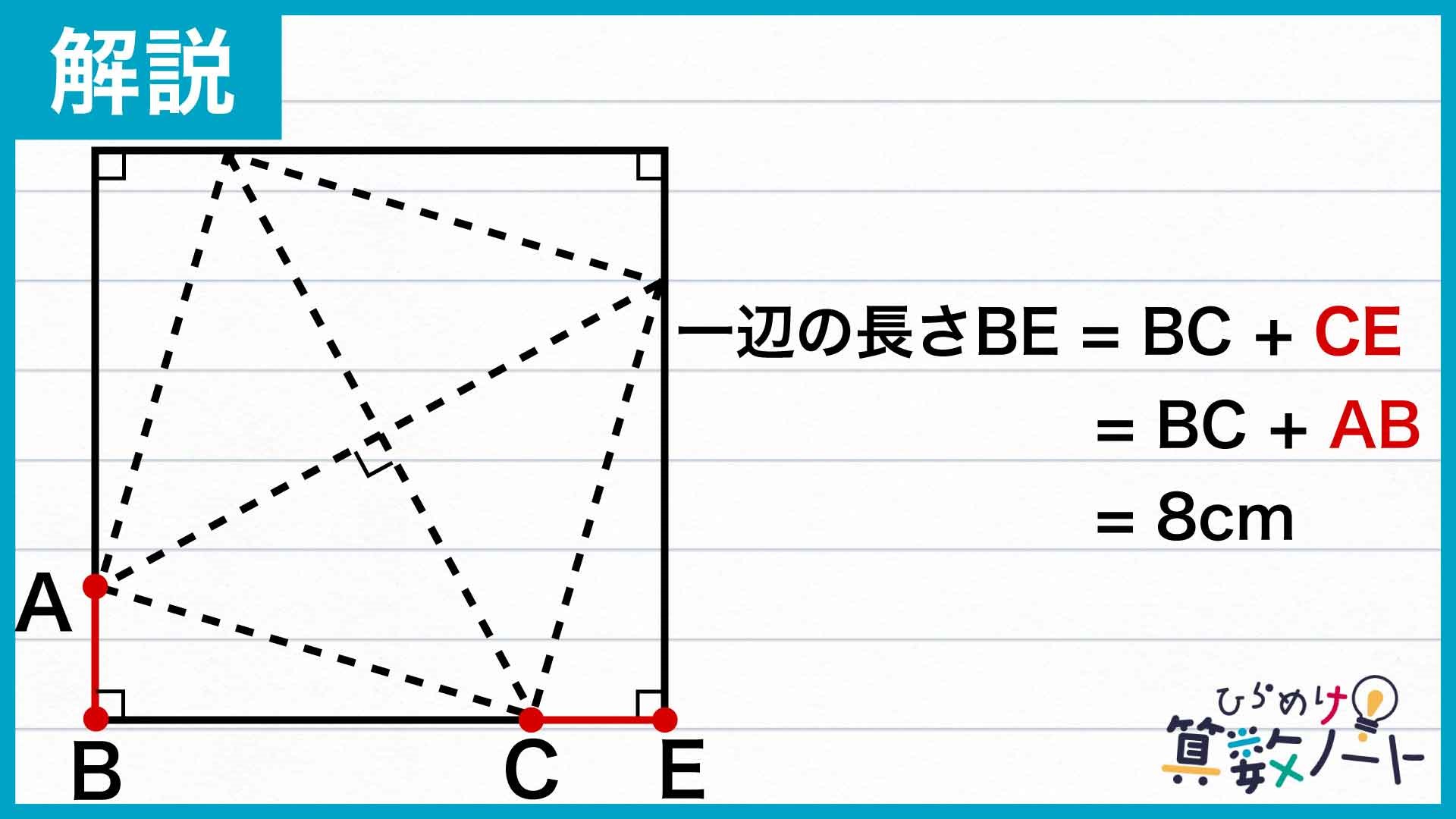
正方形の面積は、四角形ABCD4つ分の面積と同じなので、四角形ABCDの面積は64÷4=16cm²となります。

答え：16cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】