解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:自力で解きたい方はこちらへ! 以下は問題の解説です
今回の問題を解くうえで重要なポイントを以下にまとめました。
整理すると、
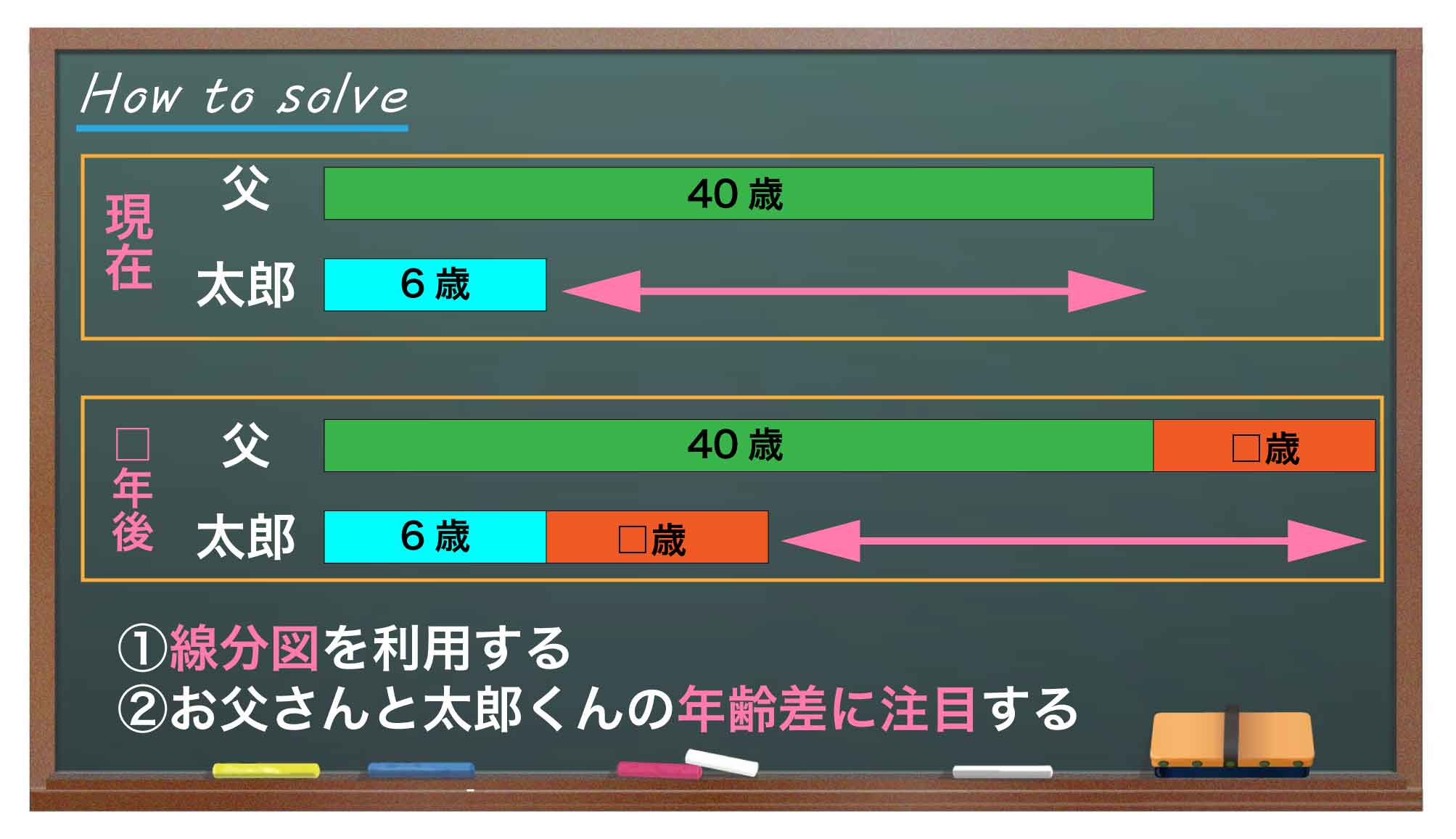
- 線分図を利用する
- 太郎くんとお父さんの年齢の差に注目する
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
線分図を利用する
説明のため、求めたい答えを「□年後」とします。下の図のように、□年後の太郎くんとお父さんの年齢を線分図にしてみます。
太郎くんとお父さんの年齢の差に注目する
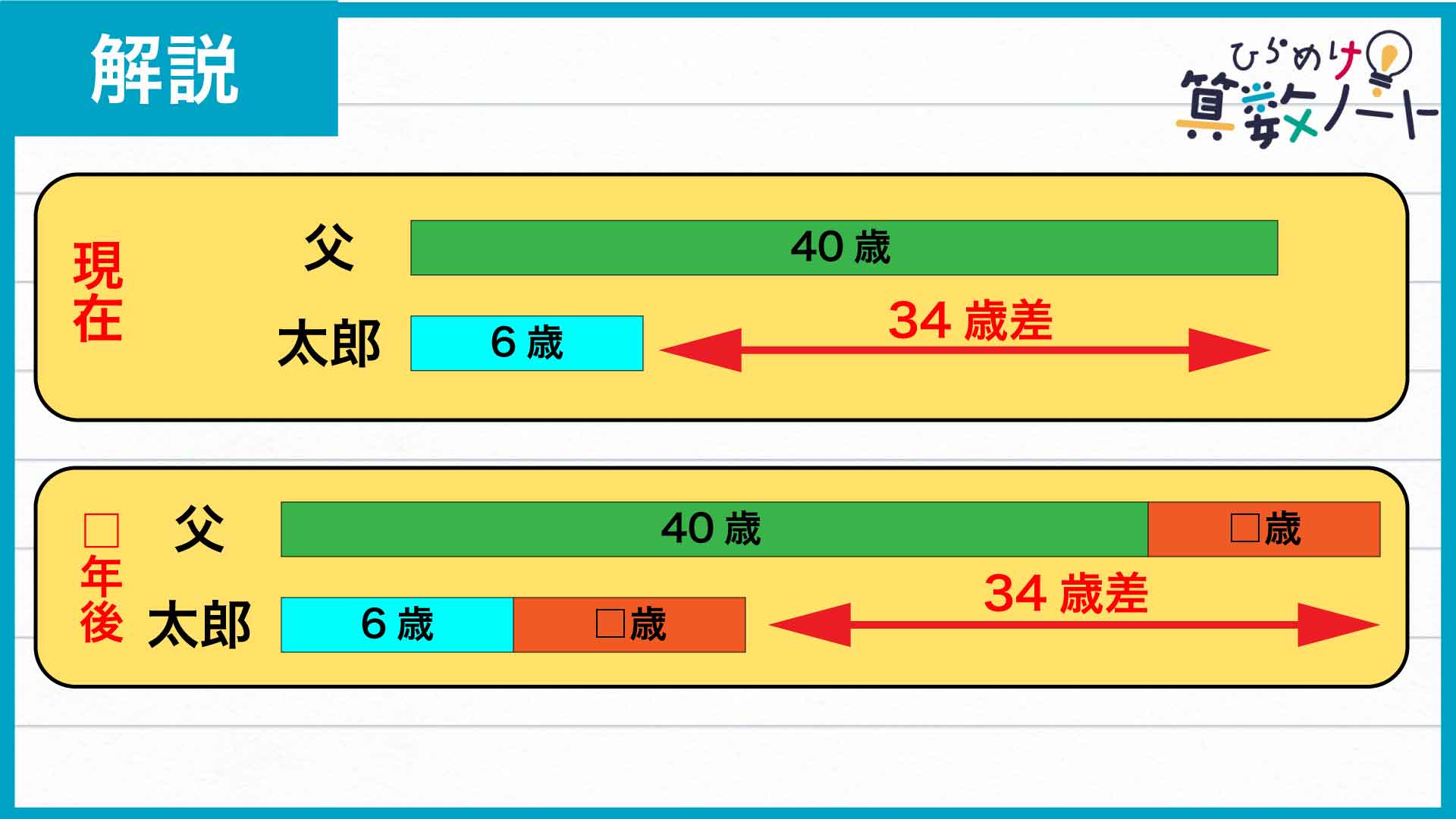
次に、太郎くんとお父さんの年齢の差に注目してみましょう。□年後には、太郎くんもお父さんも同じ□年分だけ年を取ることになります。よって、太郎くんとお父さんの年齢の差は、□年後も現在と変わらないことがわかります。
現在の太郎くんとお父さんの年齢の差は40-6=34歳なので、□年後でも太郎くんとお父さんの年齢の差は34歳であることがわかります。
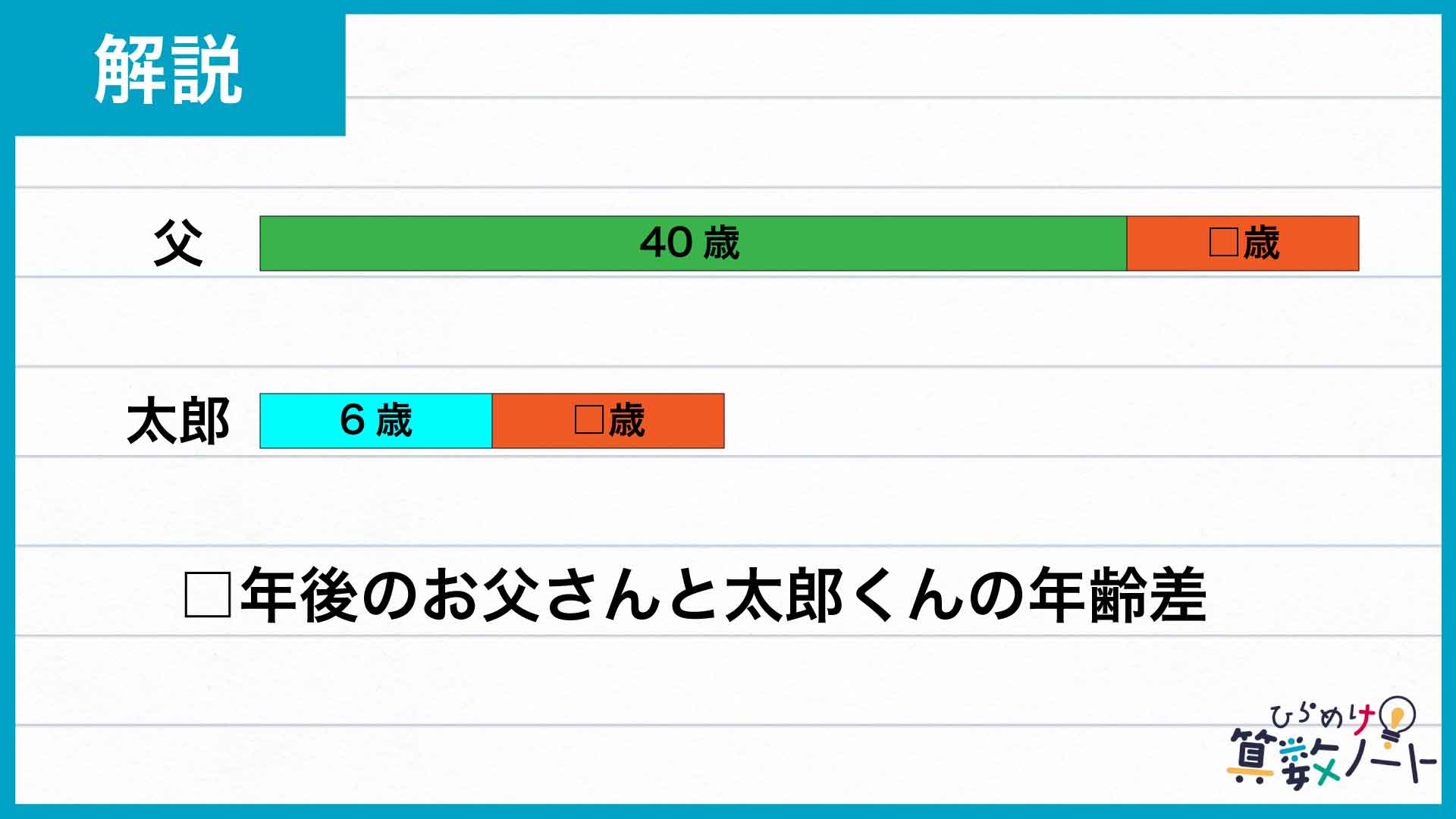
さらに、□年後の太郎くんの年齢を〇歳としましょう。すると、□年後のお父さんの年齢は問題文の条件から3×〇歳となります。よって、□年後の太郎くんとお父さんの年齢の差は、2×〇歳となることがわかります。以上のことを図にまとめると、下のようになります。
したがって、□年後の太郎くんとお父さんの年齢の差は34歳だったので、2×〇=34という等式が成り立ち、〇は17歳にあたることがわかります。
「□年後の太郎くんの年齢」を〇歳としていたので、「□年後の太郎くんの年齢」が17歳であることがわかります。太郎くんの現在の年齢は6歳なので、□=17-6=11となり、求める答えは11年後です。
答え:11年後
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】