解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
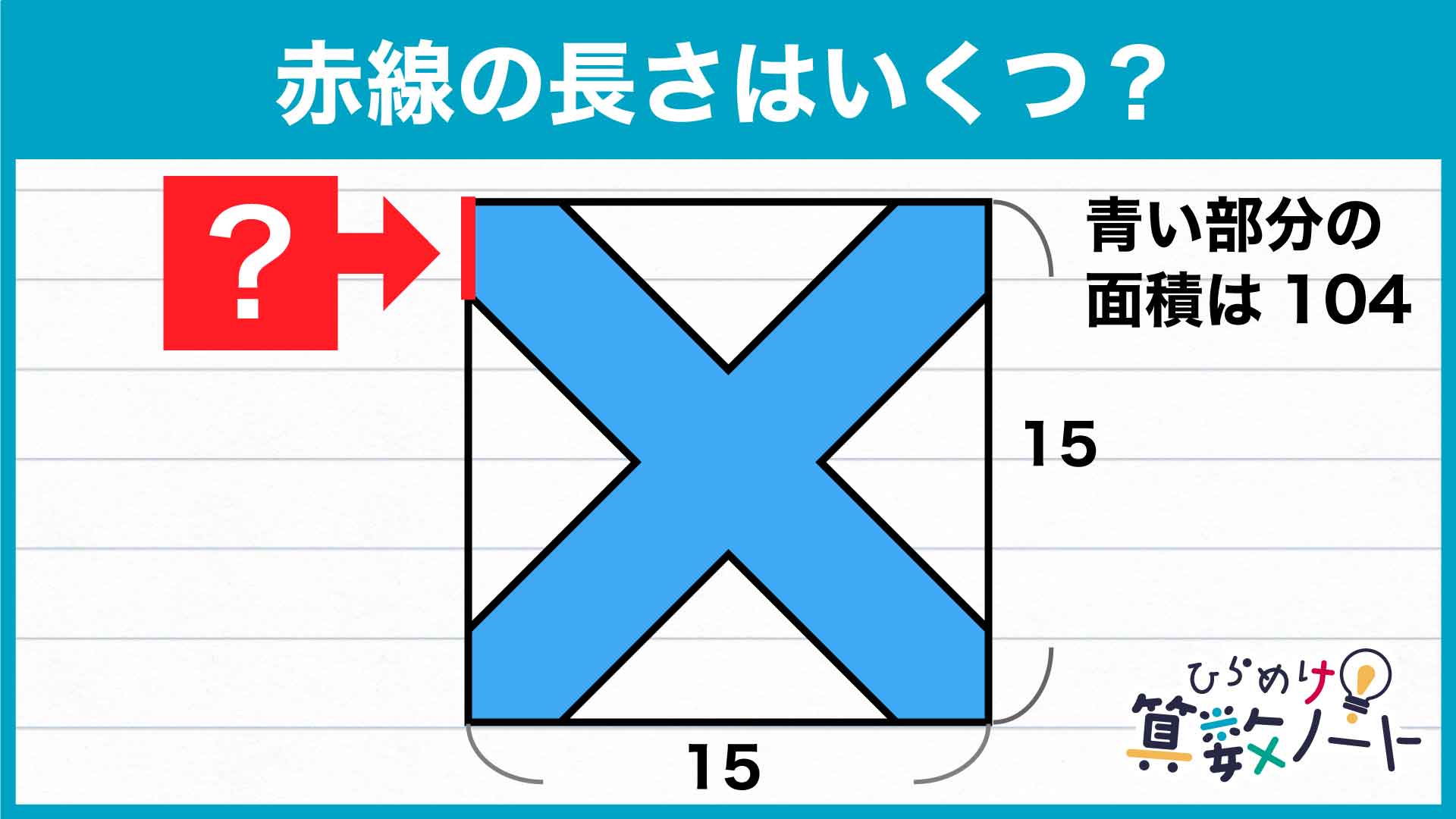
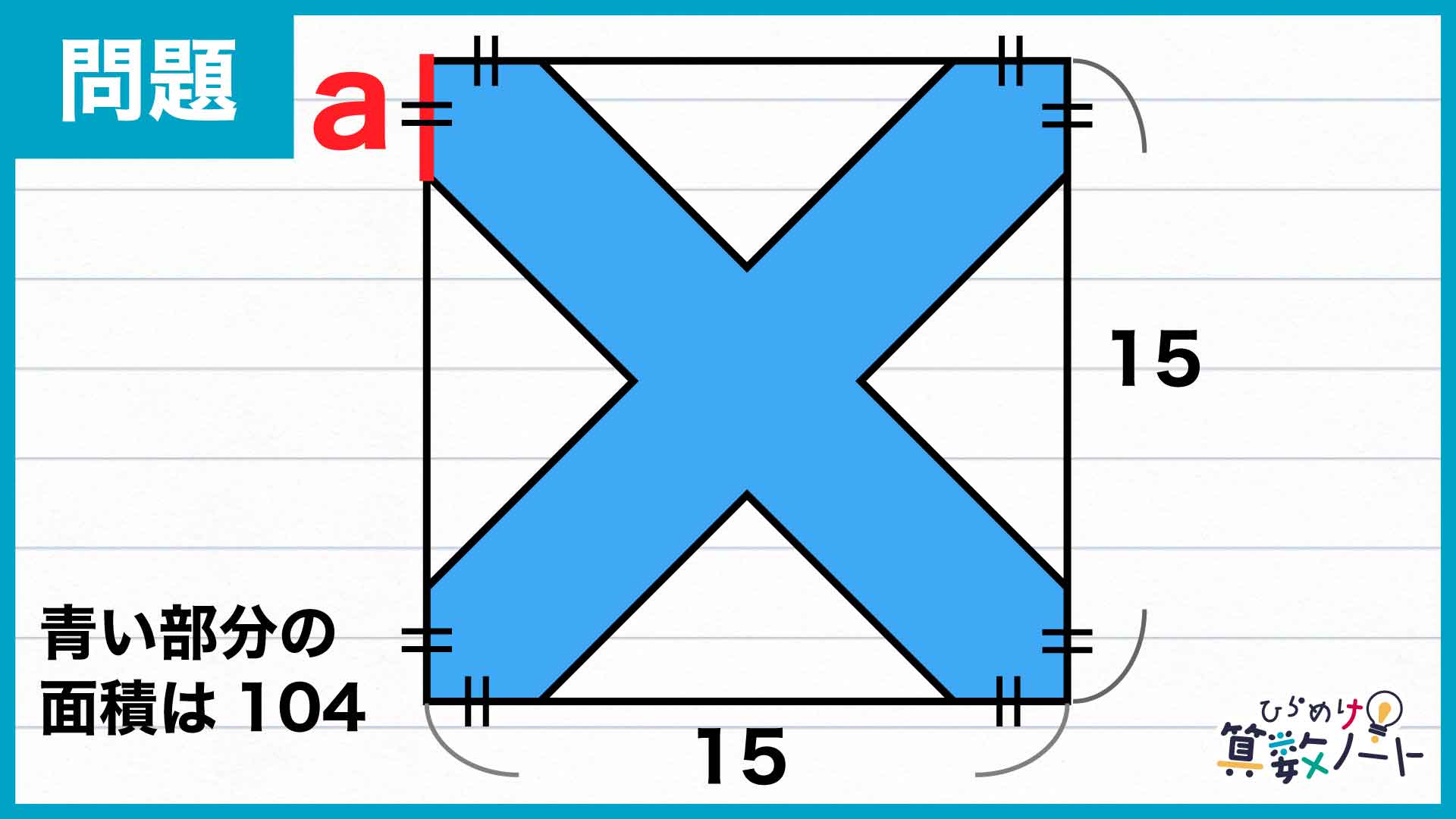
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
この問題の解き方をまとめた図がこちらです。
ポイントは、正方形から「道」の部分を除いたときにできる三角形をうまく組み合わせ、先にbの長さを求めることです。
では、このポイントを踏まえつつ解いていきましょう!
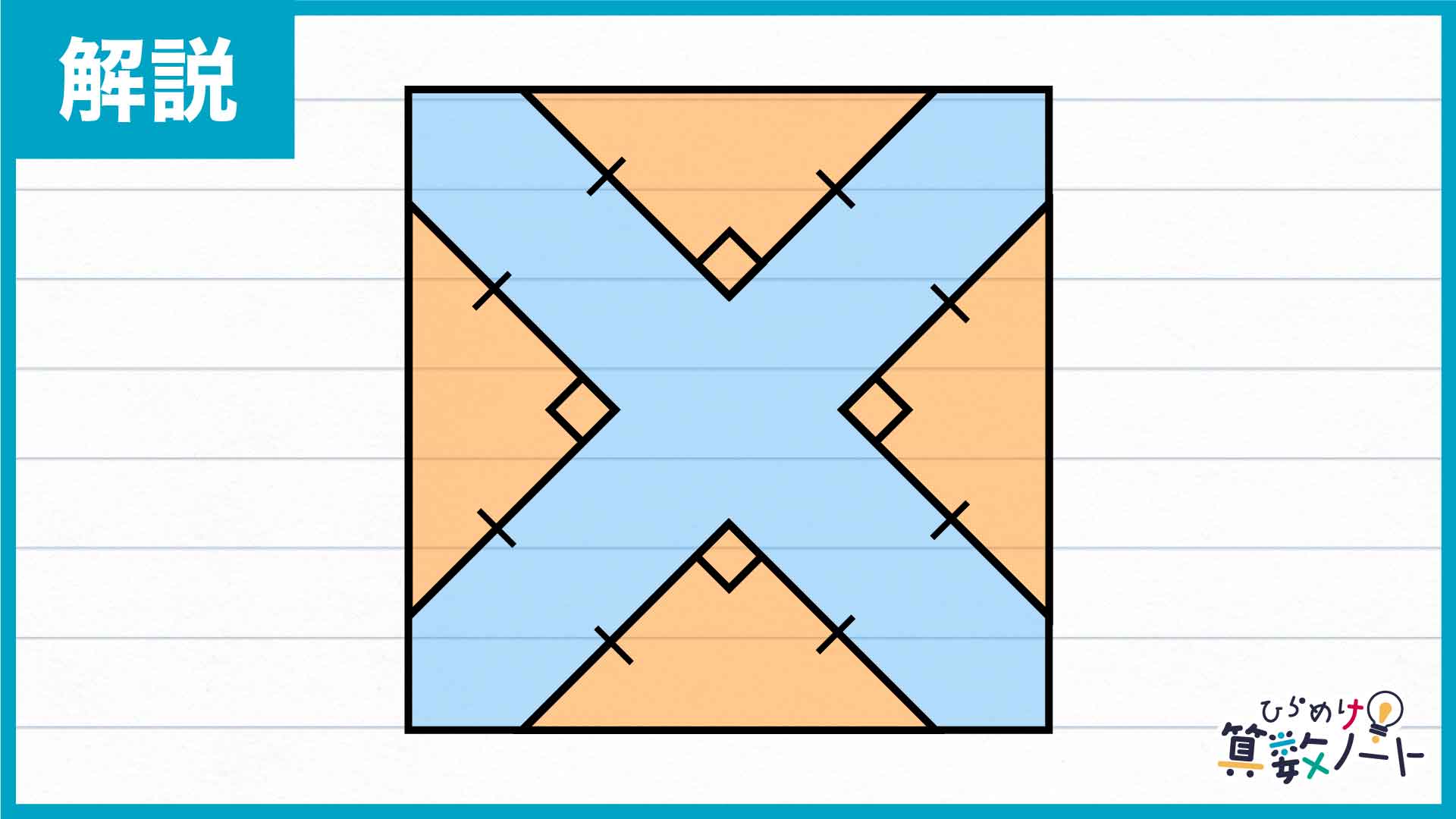
道の部分「以外」を合体させる
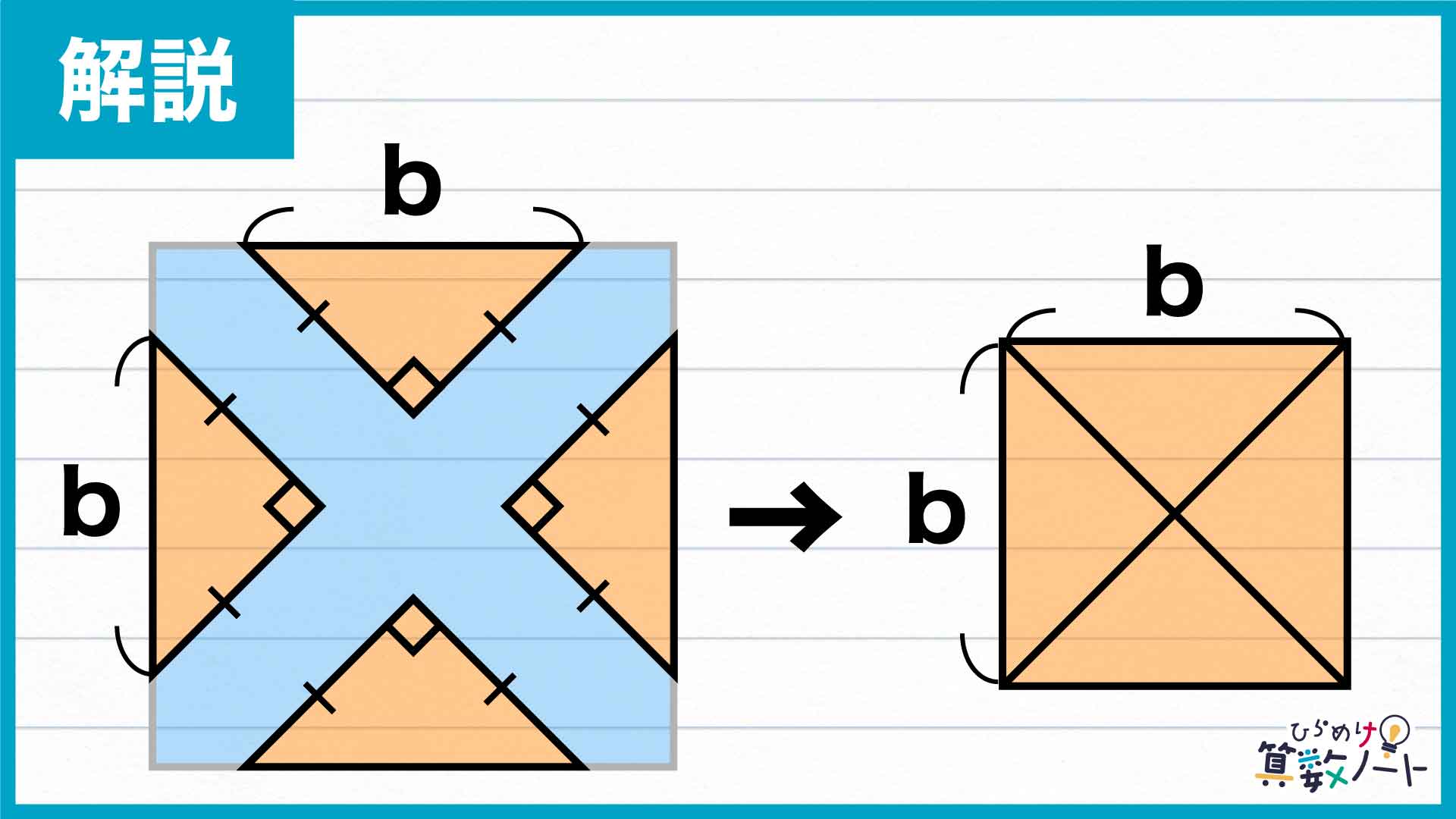
まず注目すべきは、青色の「道」の部分を除いたときにできる三角形です。今回の図形は90度ずつ回転させたり左右反転させたりしても元の図形にぴたりと一致するため、オレンジ色の三角形は全て合同な二等辺三角形といえます。
また、正方形の対角線は垂直に交わるため、それに平行な2本の道も互いに垂直であり、オレンジ色の三角形は全て直角二等辺三角形であることがわかります。
では、この4つの直角二等辺三角形を、真ん中に寄せてくっつけてみるとどうでしょうか。
すると、はじめの正方形よりもひとまわり小さな正方形ができます。直角三角形の斜辺の長さをbとすると、この正方形の1辺もまたbとなります。
正方形の面積からa、bの長さを求める
小さな正方形の1辺bを求めるには、この正方形の面積を知る必要があります。大きな正方形の1辺は15、道の部分の面積は104とわかっているので、小さな正方形の面積は15×15-104=121となります。
したがって、b×b=121であることから小さな正方形の1辺bは11とわかります。大きな正方形の1辺の長さはa×2+b=15なので、求める長さaは(15-11)÷2=2となります。
答え:2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









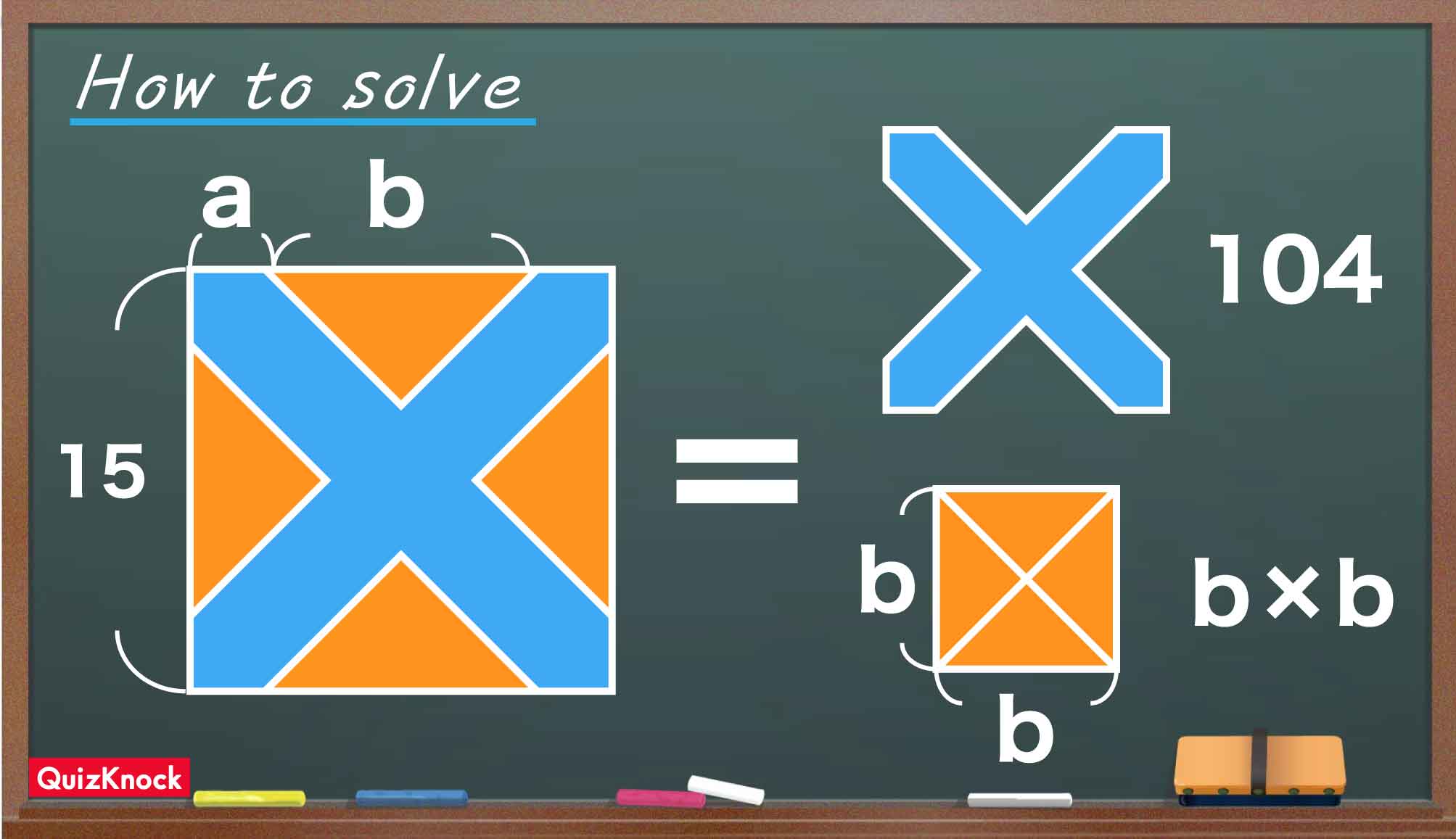

.jpg)










.jpg)







