小学生でも解ける「四角形の面積」を求める問題、あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：自力で解きたい方はこちらへ！以下は問題の解説です

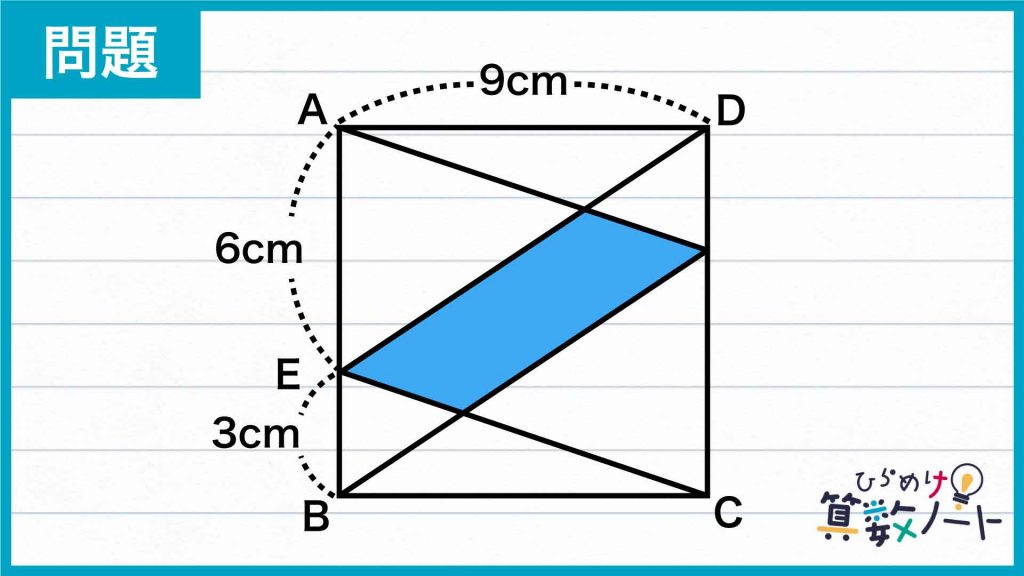
今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、

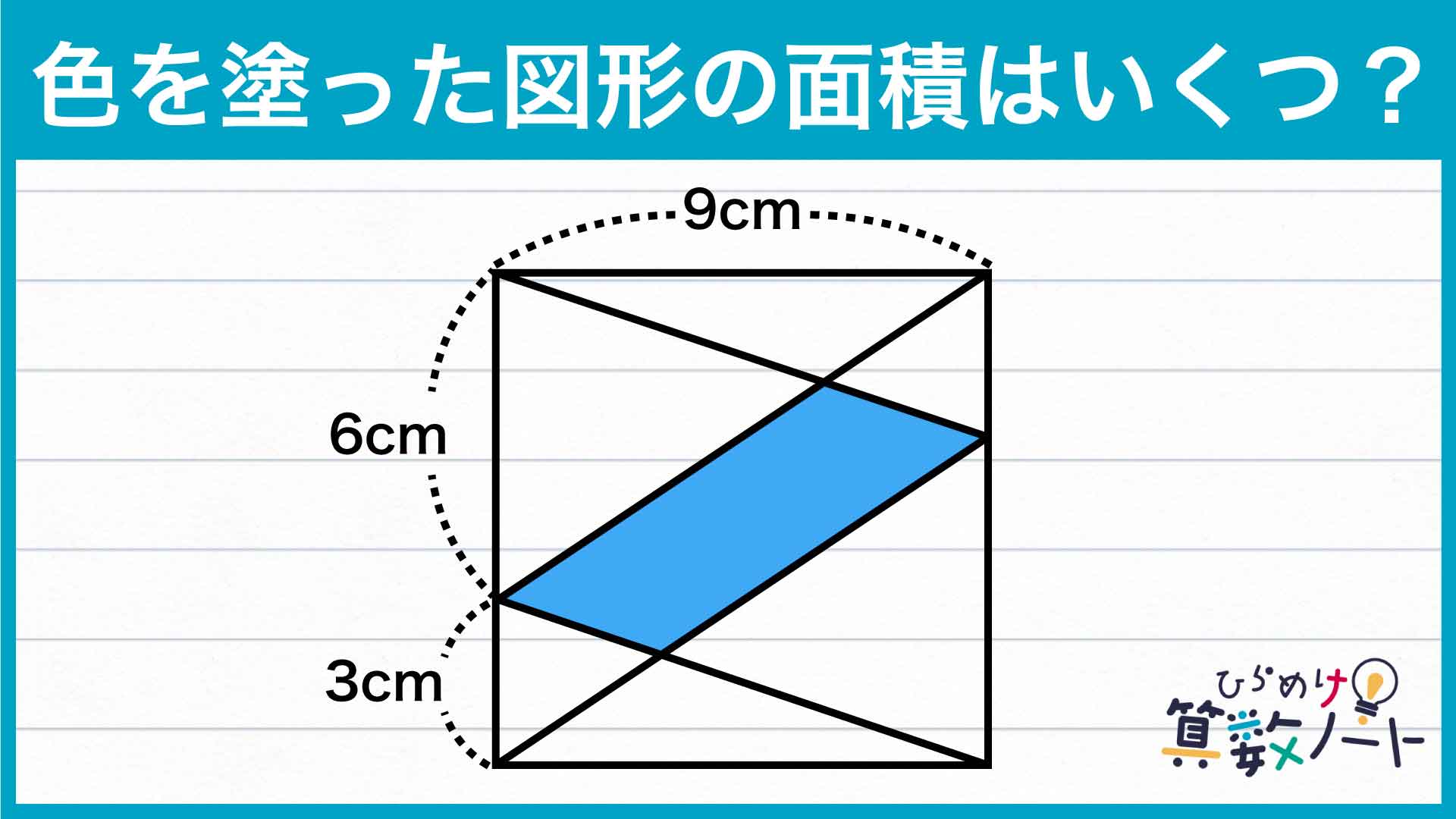
• 面積を求めたい図形（四角形EFGH）を分割する
• 「等積変形」を利用する
• 高さが同じ三角形の「底辺の長さ」と「面積」の関係を利用する

の3点です。これらのポイントを踏まえながら、問題を解いていきましょう。

面積を求めたい図形を分割する

下の図のように四角形EFGHを三角形EFGと三角形EHGに分割します。

ここで、AGとEC、DEとGBがそれぞれ互いに平行であることから四角形EFGHは平行四辺形となるので、平行四辺形の性質から三角形EFGと三角形EHGの面積は等しくなります。

ということは、この2つの三角形のうちどちらかの面積を求めることができれば、それを2倍することで答えを導くことができます。

「等積変形」を利用する

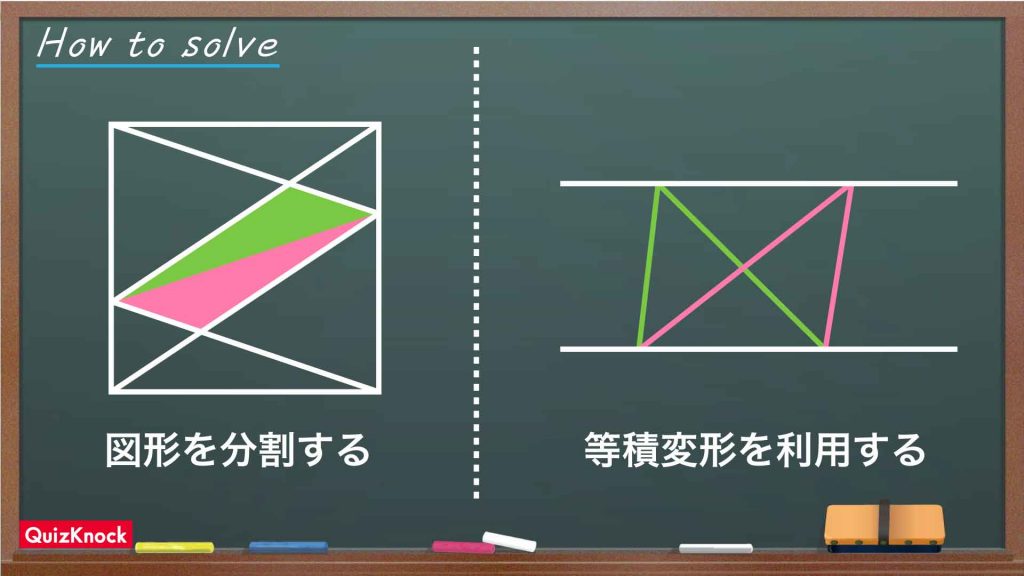
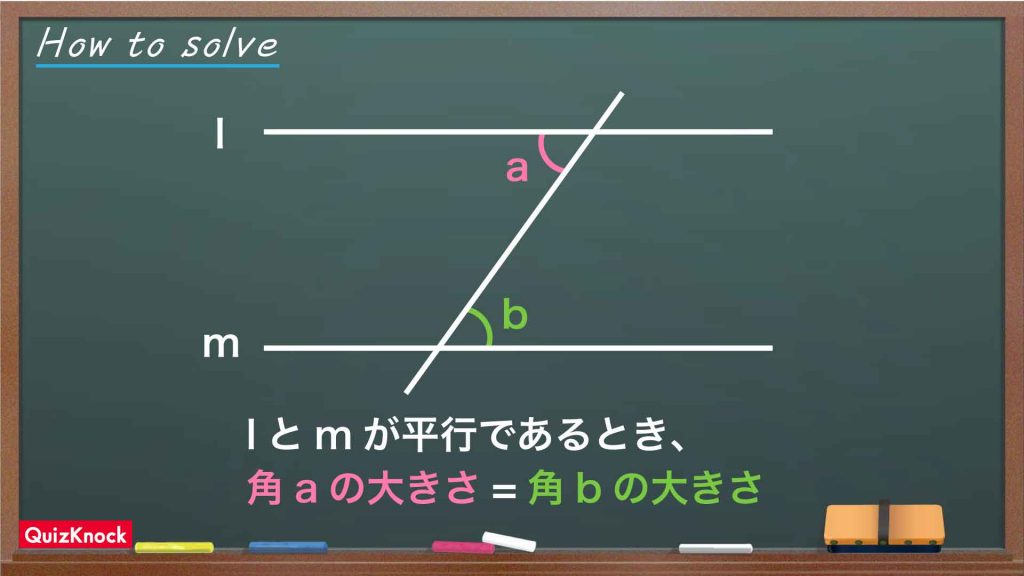
では、三角形EHGの面積を求めていきましょう。ここで、次のような性質を利用します。

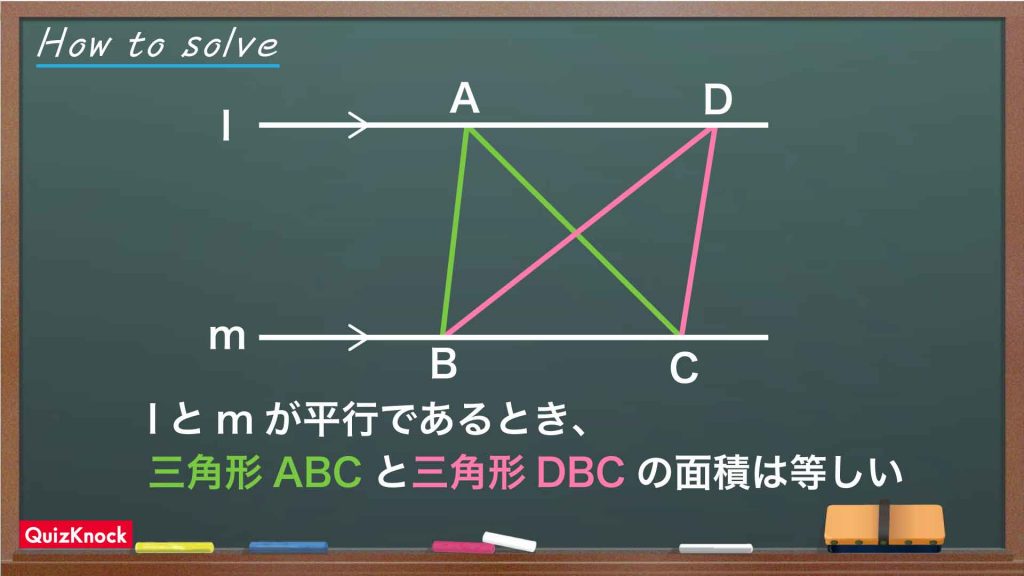
この性質を利用して、図形の面積を変えずにその図形を変形することを「等積変形」と呼びます。

問題の図において、三角形EHGは、平行な線分であるAG、ECの間にあるので、下の図のように三角形EHGを等積変形することができます。

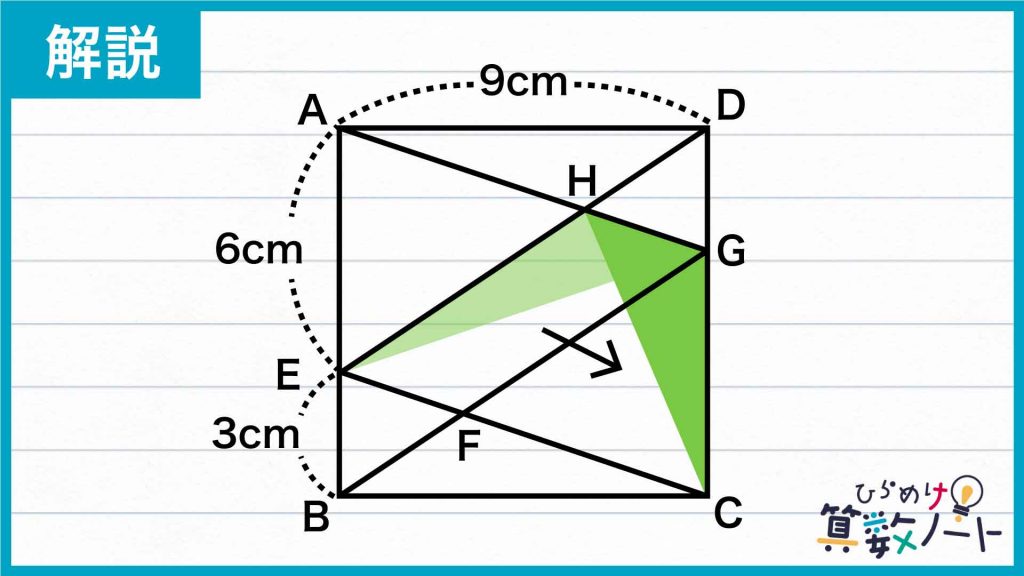
すると、三角形EHGの面積は三角形CHGの面積と等しくなります。

三角形CHGの面積を求める

次に、三角形CHGの面積を求めます。ここで、次のような性質を利用します。

まず問題の図で、AEとDGは平行です。よって、平行線についての「錯角の関係」から、角AEHと角GDH、角HAEと角HGDの大きさはそれぞれ等しいことがわかります。

また、角EHAと角DHGは対頂角の関係にあり、その大きさは等しいので、「対応する3つの角の大きさがそれぞれ等しい」ことから、三角形AEHと三角形GDHは相似の関係にあることがわかります。

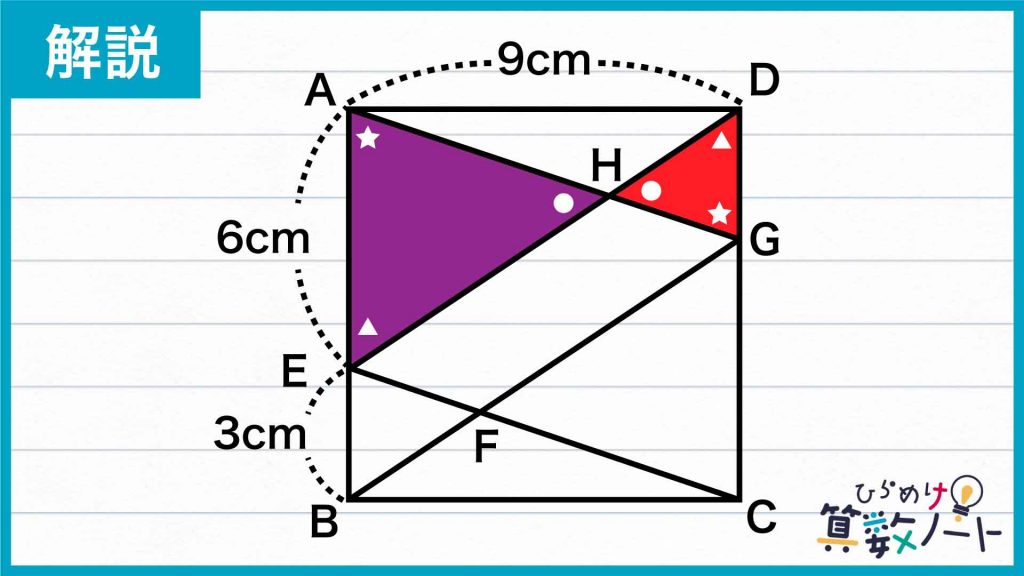
相似な図形の「対応する辺の比はそれぞれ等しい」ので、三角形AEHと三角形GDHの対応する辺の比は、辺AEが6cm、辺GDが3cmであることから6:3=2:1になります。

よって、AHの長さとGHの長さの比も2:1になります。次に、下のような性質を利用します。

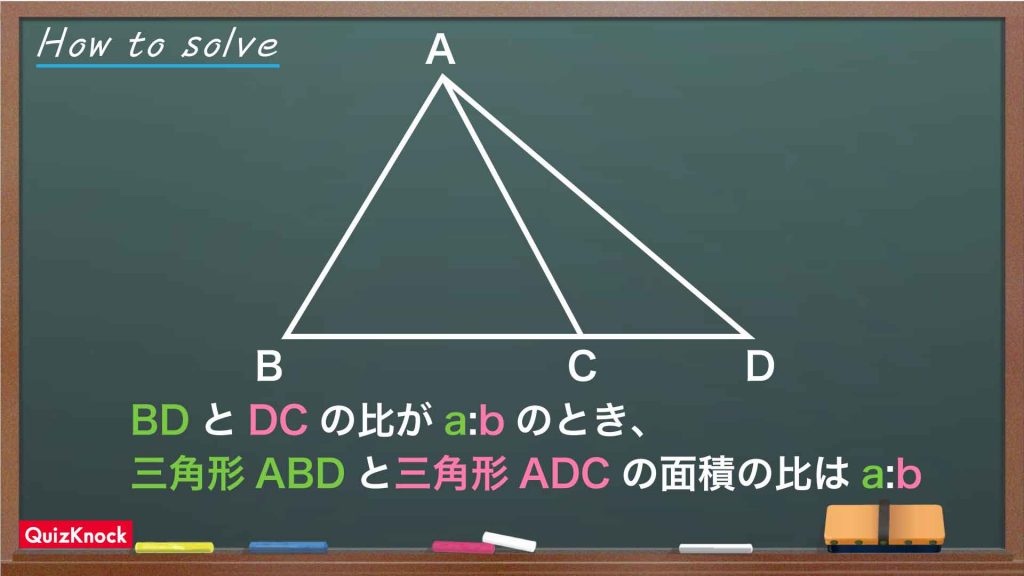
上の性質を利用すると、AH:GH=2:1であることから、三角形CHAと三角形CHGの面積の比は2:1になります。

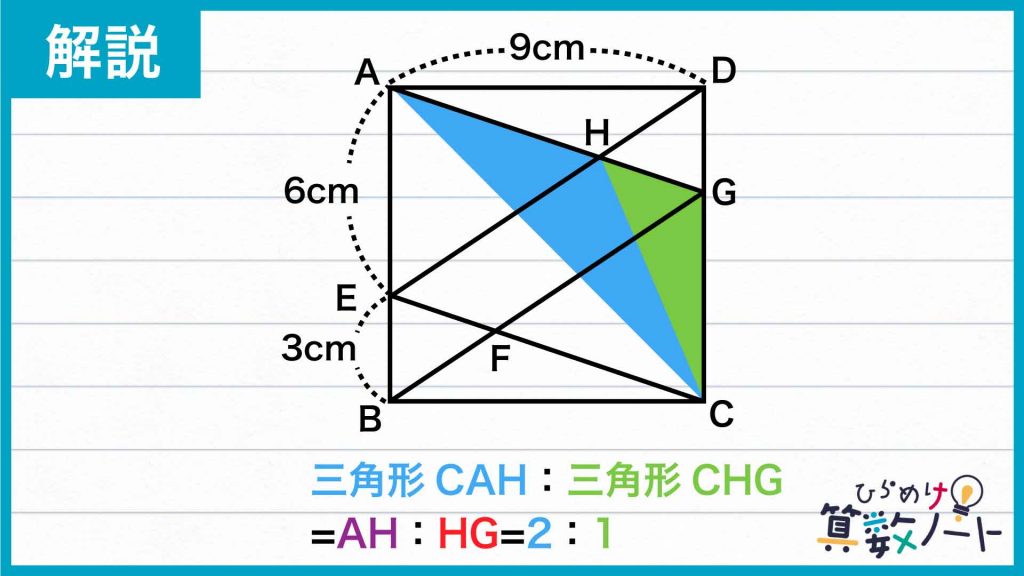
よって、三角形CHGの面積を△とすると、三角形CAGの面積は「3×△」と書けます。

ここで、平行四辺形AECGに注目してみましょう。平行四辺形AECGの面積は、9×6=54cm²です。平行四辺形の性質から、三角形CAGの面積は平行四辺形AECGの面積の半分であり、その面積は27cm²となります。

よって、3×△は27cm²であるので、△は9cm²に当たります。したがって、三角形CHGの面積は9cm²であり、三角形EHGの面積も9cm²になります。

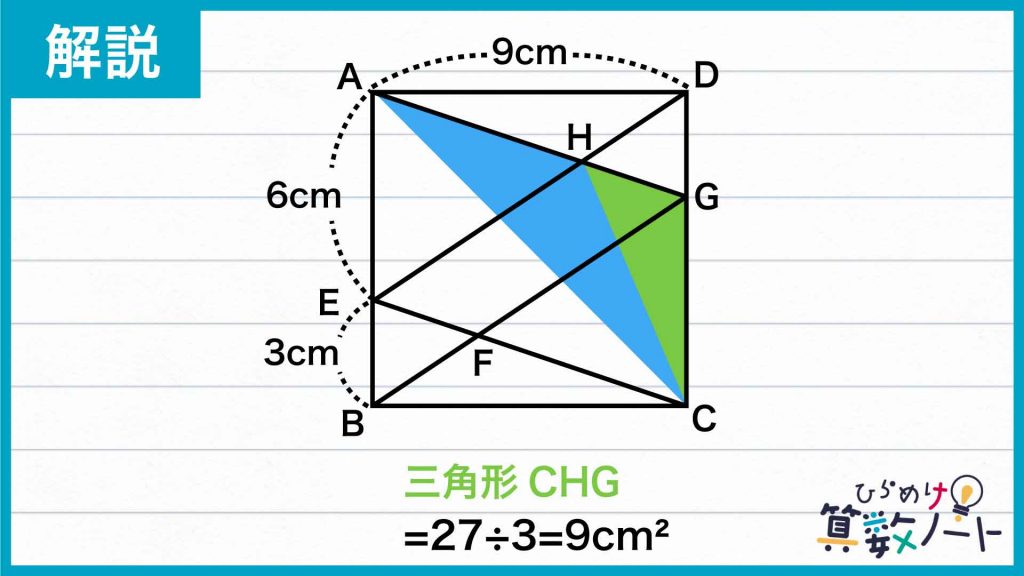
よって、求めたい図形の面積は、三角形EFGと三角形EHGの面積が等しいことから、9×2=18cm²となります。

答え：18cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】