解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
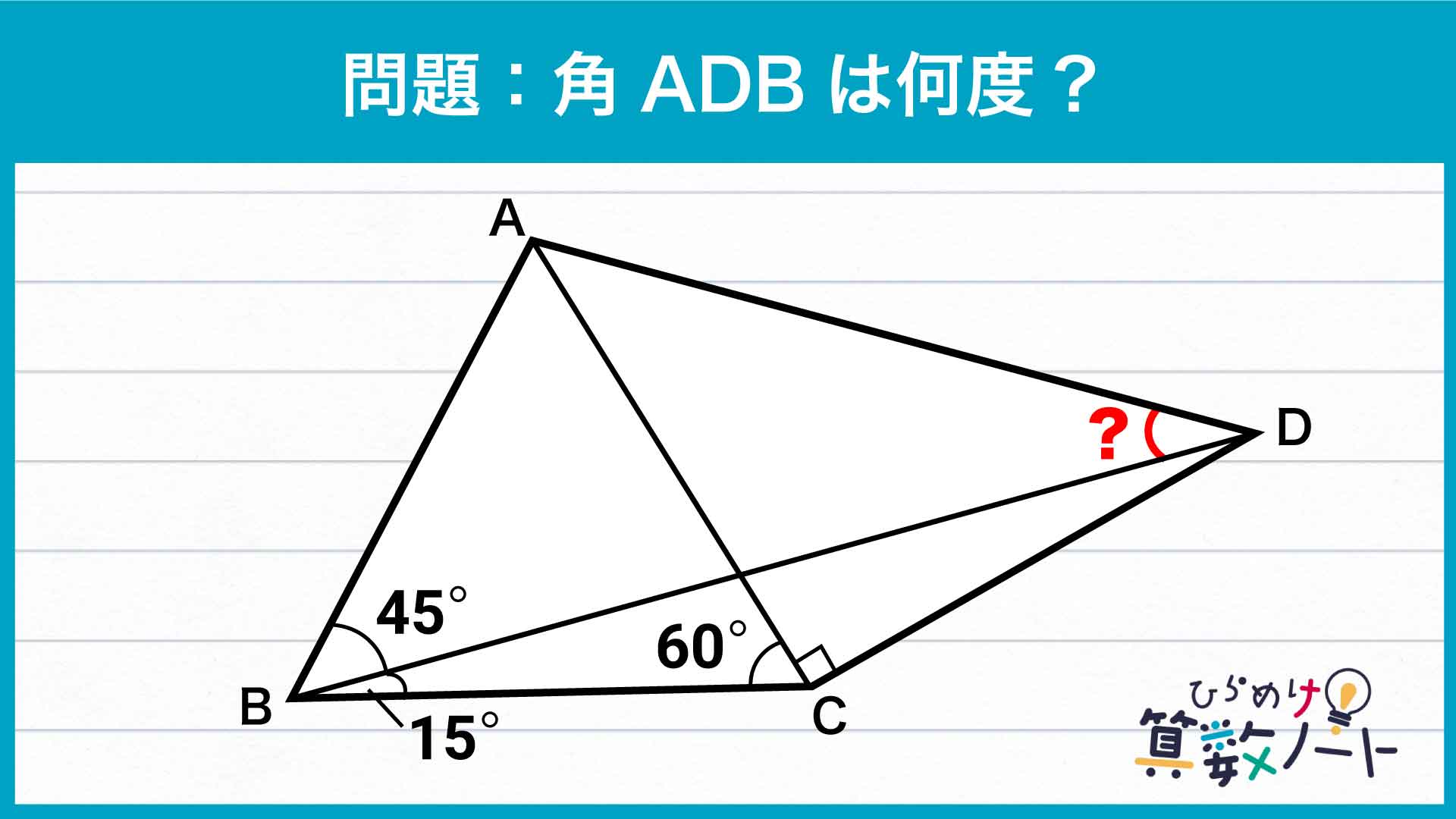
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
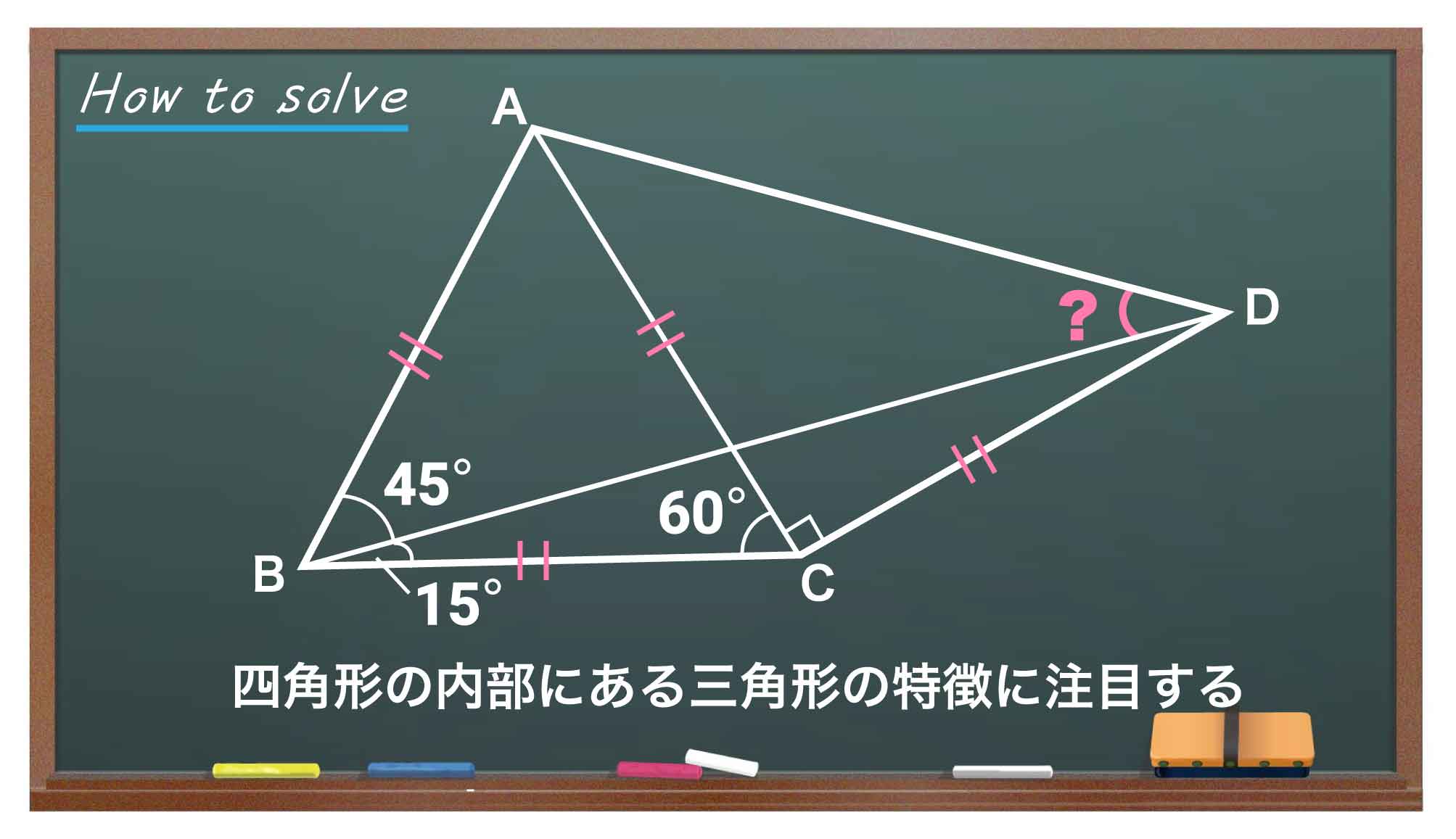
今回の問題の解き方をまとめた図がこちらです。ポイントは四角形の内部にある三角形の特徴に注目することです。
このポイントをもとに、解いていきましょう!
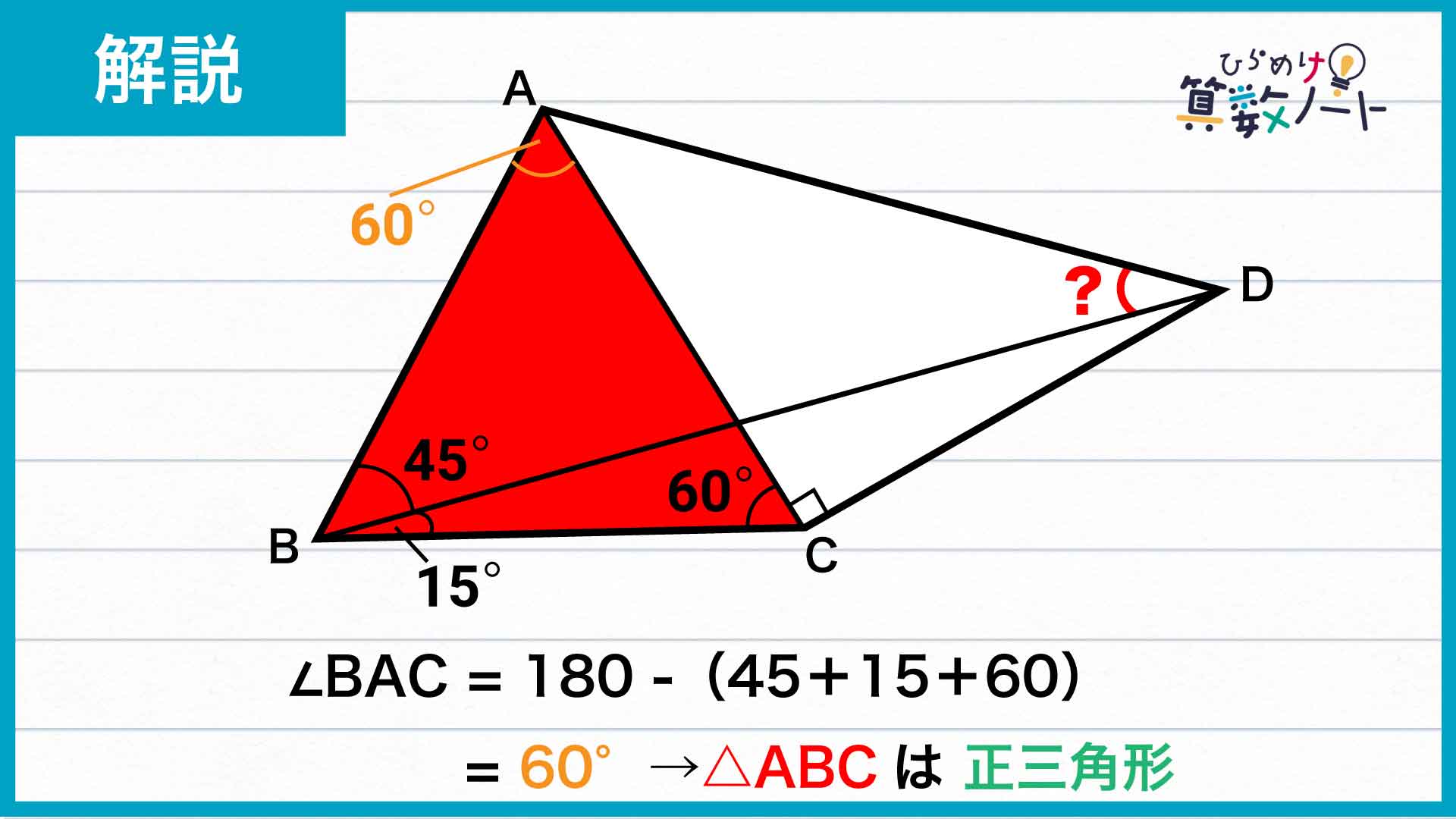
三角形ABCはどんな三角形?
まずは、三角形ABCに着目します。
三角形の内角の和は180度であることから、角BAC=180-(角ABC+角ACB)=180-(45+15+60)=60度であることがわかります。
したがって、三角形ABCの3つの内角すべてが60度であることから、三角形ABCは正三角形です。
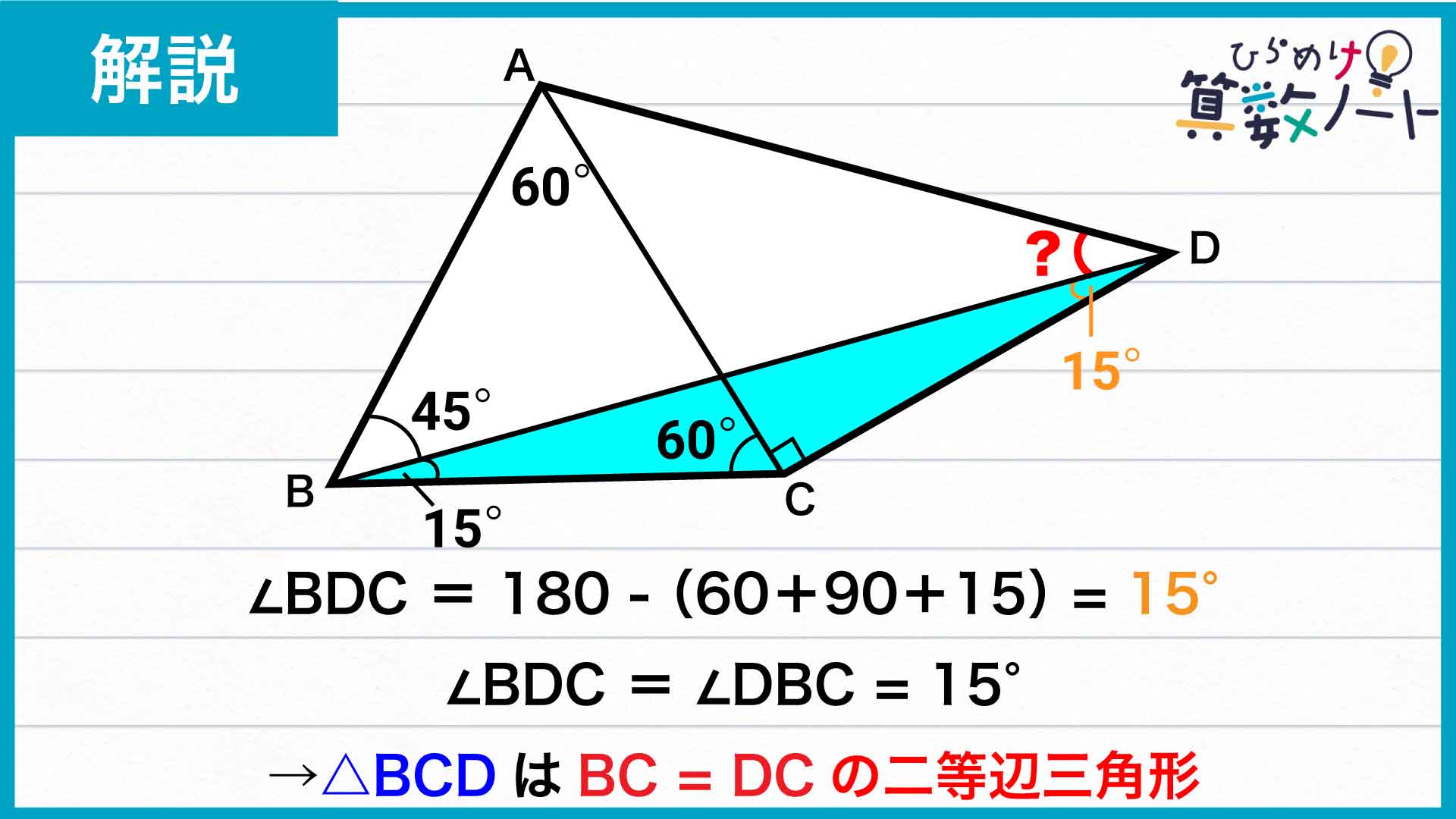
三角形BCDに注目!
次に、三角形BCDに注目しましょう。
三角形の内角の和は180度であることから、角BDC=180-(角BCD+角DBC)=180-(60+90+15)=15度です。
角BDC=角DBC=15度であることから、三角形BCDはBC=DCの二等辺三角形であることがわかります。
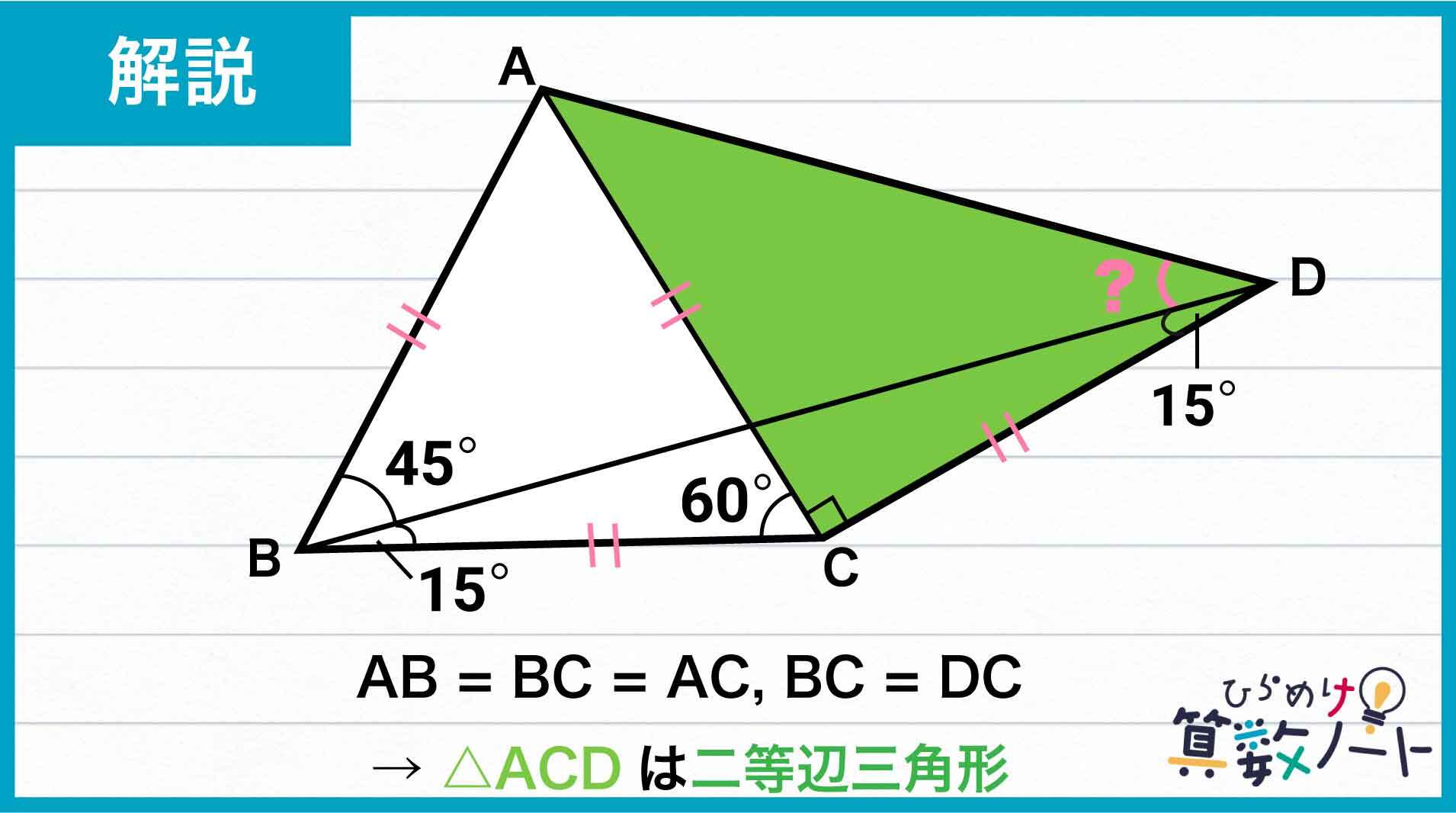
三角形の辺の長さに注目!
三角形ABCは正三角形なのでAB=BC=ACです。また、BC=DCであることも確認しました。
辺ACと辺DCは、いずれも辺BCと長さが等しいことから、三角形ACDは二等辺三角形であることがわかります。
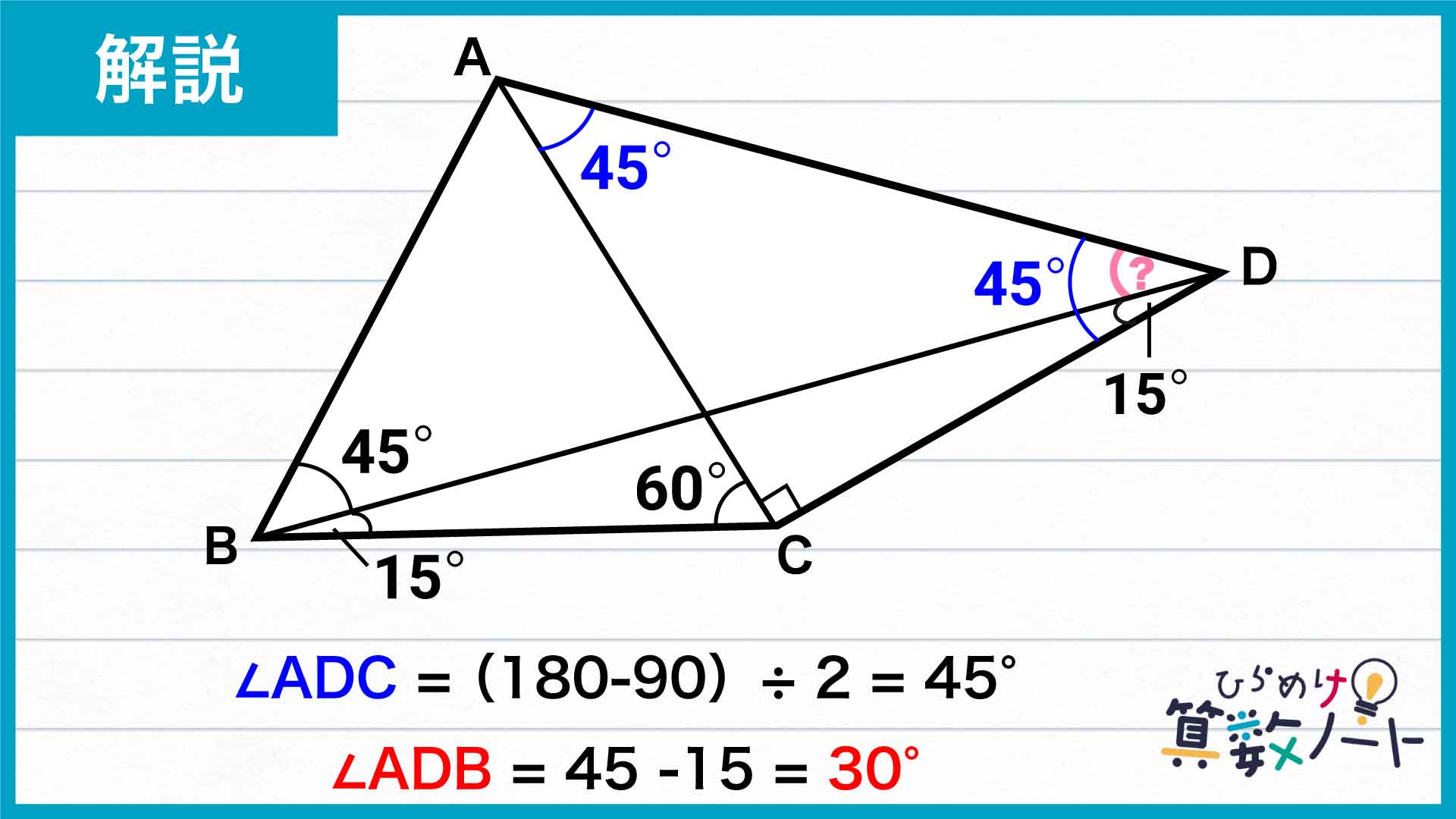
三角形ACDの内角の和は180度であり、また、角ADC=角DACであることから、角ADC=(180-角ACD)÷2=(180-90)÷2=45度です。
角ADBは、角ADCから角BDCを引くことで求められます。角ADB=角ADC-角BDC=45-15=30度です。
答え:30度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









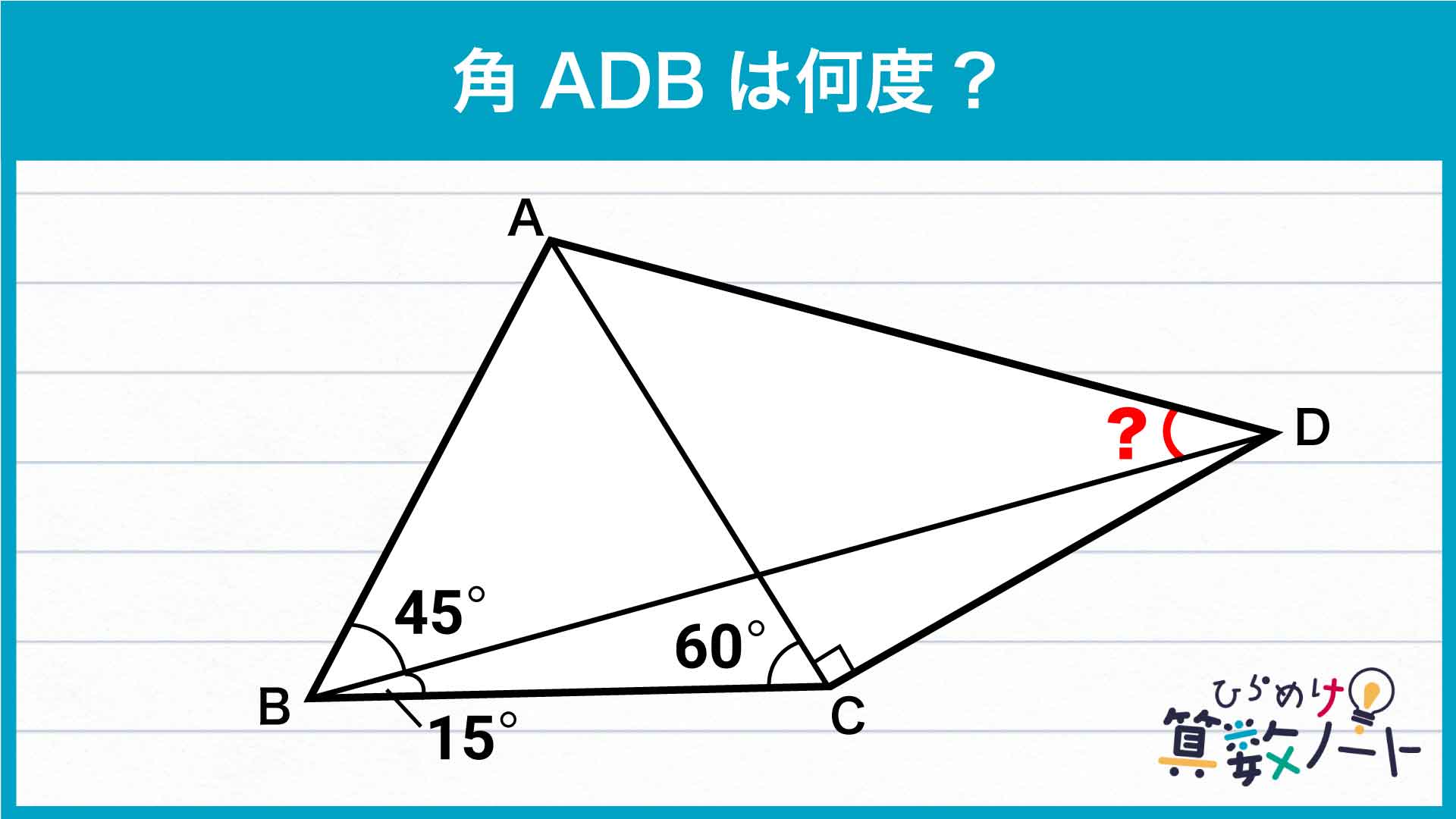

.jpg)








.jpg)







