【ワンピース】ルフィの腕が輪ゴムと同じ素材ならどのくらい伸びる？

コジマです。

『ONE PIECE』の主人公モンキー・D・ルフィは「ゴムゴムの実」の能力者。ゴムのように自在に伸び縮みする身体で敵を蹴散らす。

ところで、ルフィは身体をときに数十メートルまで伸ばすが、細くてよく伸びる輪ゴムでもそんなには伸びない。つまり、ルフィの身体はゴムっぽい何かであって、ゴムそのものではないのかもしれない。

それでは、もし輪ゴムと同じ素材だとしたらどのくらい伸びるのか？

問題設定

実はゴムといっても、輪ゴムのように伸びるものだけでなく、硬いもの、熱への耐久性に優れたものなどいろいろな種類がある。輪ゴムの原材料は天然ゴムで、特に伸び率が大きいゴムだ。

そこで、ルフィの腕が天然ゴムでできていたら、と仮定して考える。

引用：モンキー・D・ルフィ｜ONE PIECE.com

ルフィの身長は174cmで、立ち絵から腕の長さは85cmくらいだろう。太さまで推測するのは難しいが、ルフィは細身なので直径9cmくらいだとする。

腕を底面の直径が9cm、高さが85cmの円柱形の天然ゴムとすると、腕はどのくらい伸びるのだろう？

※全身がゴムなら腕だけでなく全身が伸びるはずだが、ここでは腕だけがゴム化したとして、ゴムの腕で全体重を吊る状況を考えることにする。

いざ計算

ゴムの伸びは引っ張る力に比例する、つまり引っ張る力を2倍にすると2倍伸びる。また、ゴムは太さ（断面積の大きさ）に反比例して伸びにくくなる、つまり断面積が2倍になると伸びが0.5倍になる。

この関係性を数式で表すと次のようになる。

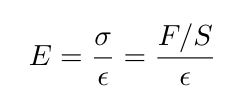
σは応力、つまり単位面積あたりの引っ張る力の強さで、引っ張る力をF、断面積をSとすればσ=F/Sとなる。今回の例で言えば、断面積は直径9cmの円なので(9/2)*(9/2)*π=63.6平方cm（0.00636平方m）。

εはひずみといい、要するに伸びの大きさのこと。元の長さに比べて伸びる割合を表す。

Eはヤング率と呼ばれ、ゴムの種類によって変わる。この値が小さいほど、同じ力でもより伸びるゴムということになる。天然ゴムのヤング率は、こちらによると0.1MPa（メガパスカル）〜10MPa。今回は間をとって1MPaとする。

上の式を変形すると、ε=F/ES。ここにF=1N（ニュートン）、E=1MPa、S=0.00636平方mを代入すると、ε=0.000157。つまりルフィの腕は1Nの力で0.0157％伸びる！

……ピンと来ないので、もっと具体的に計算してみる。

天然ゴムルフィが片腕で鉄棒にぶら下がったとき、腕は（ルフィの体重）×（重力加速度）の力で引っ張られる。ルフィの体重は公称されていないので適当に60kgとする。重力加速度は9.8m/s^2なので、加わる力は588N。先程の値をかけると、伸び率は9.24％。腕の長さが85cmなら7.9cm伸びる！

パンチはマッハ3.7

ルフィのスケール感からすると、腕がたった7.9cm伸びるのではあまりにも寂しい。

そこでこういう問題を考えてみる。腕をもっと、例えば10m伸ばして開放したとき、拳はどれだけ速くなる？

※ここでも伸びるのは腕だけとして、腕の先端についた拳をおもりに見立ててそのスピードを考えることにする。

力学では、力を加えて伸ばしたゴムには位置エネルギーが蓄えられていると解釈される。この位置エネルギーが運動エネルギーに変換される過程を考えることで、腕の伸びが0になったときの拳の速度が下の画像のように求まる。

拳の質量mは、こちらを参考に体重の0.8%、0.48kgと推定。これを上の式に代入すると、拳の速度は1250m/s、つまりマッハ3.7！

ルフィらしいすごい値が出たが、そもそも自力でどうやって10m伸ばすのだろう。パンチの勢いで腕を伸ばすなら、必要なパンチの速さもマッハ3.7。なら直接殴ればいいのでは……。