コジマです。
そういえば一時期、囲碁やチェスといったマインドスポーツをオリンピック競技にしようという動きがあった。最近では競技性のあるテレビゲーム、いわゆるeスポーツでも同様のことが起きている。
実際に正式種目として採用された例はないものの、可能性はゼロではないだろう。今から囲碁やゲームを極めればオリンピアンも夢ではない。
むしろ、自分が得意な分野を競技化してIOCに働きかけてしまえばいいのでは……？
自分が得意な分野って何だ……？“一筆書き”とかか？
一筆書きの攻略法！？
恐らく誰もが一度はやったことがあるのではないかと思うが、一筆書きとは「線で描かれた図形を、ペンを一度も紙から離すことなくなぞること」を指す。通常は同じ線は1回しかなぞれない。
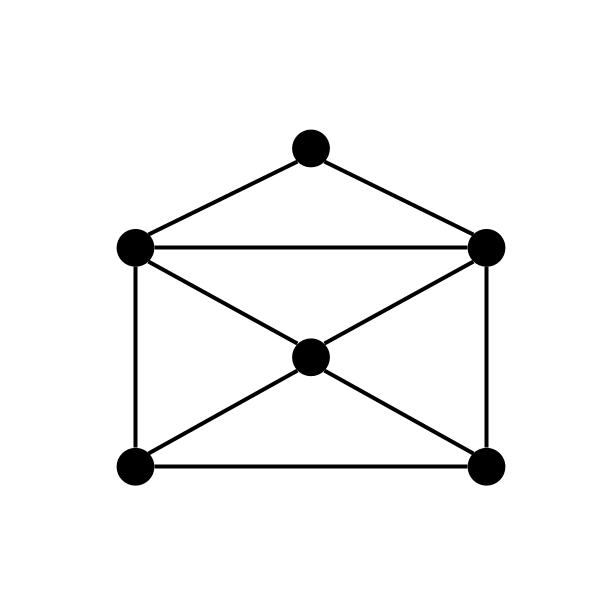一筆書きできる図形最初は試行錯誤して解いていくと思うが、トップ一筆書きマンを目指すにはそれでは遅い。まずは一筆書きの攻略法を心得ておこう。
実は、「その図形が一筆書きできるかどうか」は、「図形の各頂点に繋がっている辺の数」を調べれば判定できる。
A: すべての頂点が偶数個の辺と繋がっている
B: ちょうど2つの頂点だけが奇数個の辺と繋がっている（他は偶数個）
のいずれかを満たしている図形は必ず一筆書きできるのだ。また、逆に一筆書きできる図形は必ずAかBを満たす。下にそれぞれに当てはまる図形の例を載せたので、一筆書きができることを確かめてみよう。
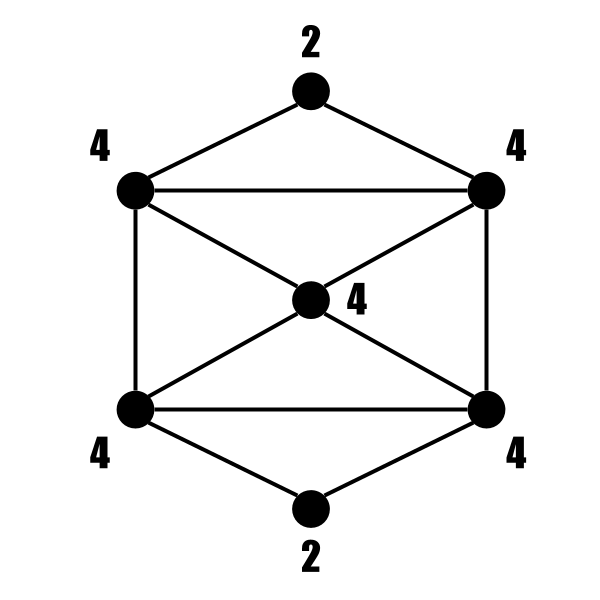Aを満たす図形の例
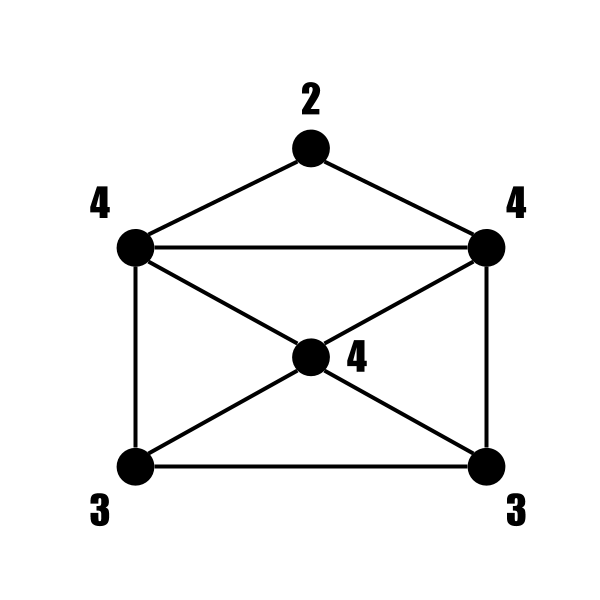Bの条件を満たす図形の例理由、説明できる？
さも隠された真実のように語ってしまったが、その道では結構有名な話である。
しかし、もともとこの性質を知っていた人も、これがどうして本当に成り立つのかを説明できるだろうか。真の一筆書きマンとなるためには覚えておきたいところなので、ここで確認しておこう。
【説明】
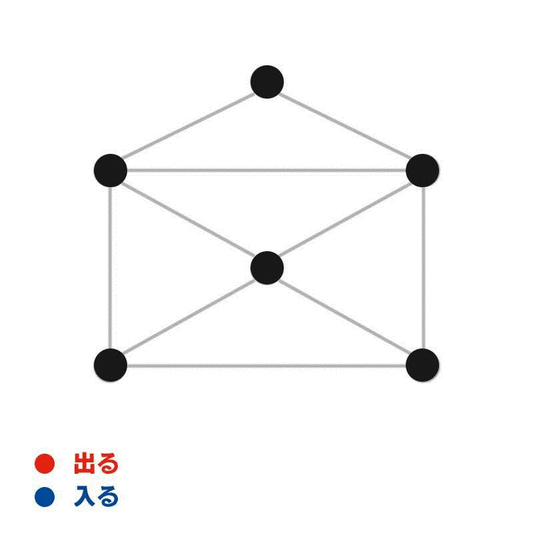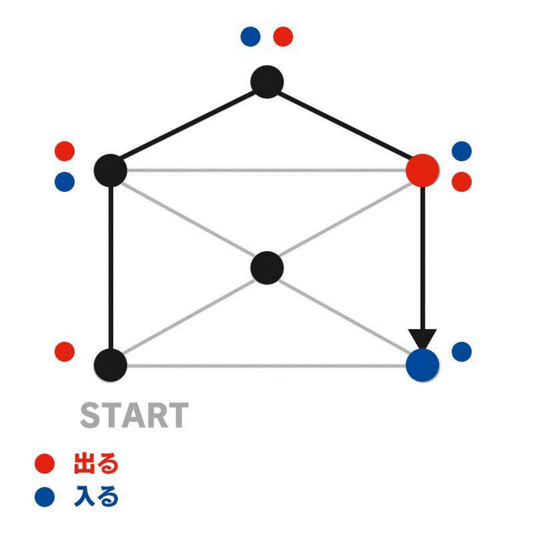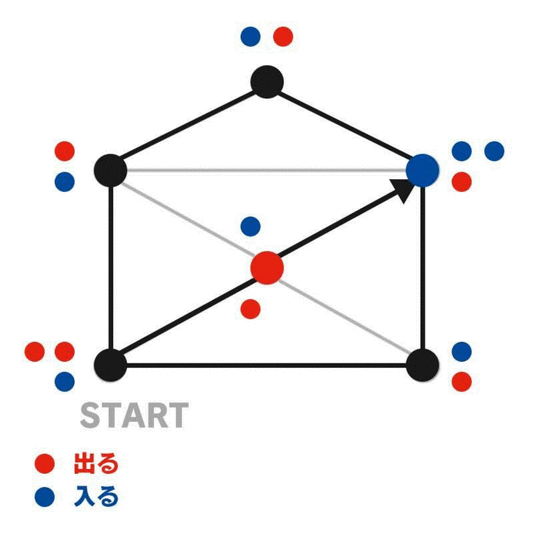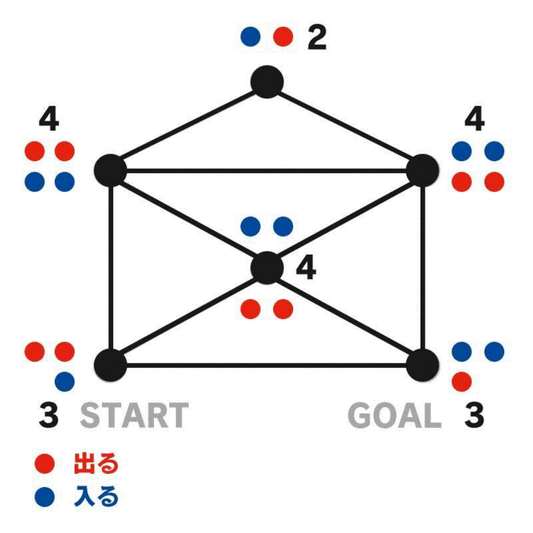
適当な図形の適当な頂点を選んで、そこから辺をなぞっていく。すると、道中の頂点を通るたびに「入る」と「出る」を1回ずつ繰り返すことが分かる。一方で、最初の頂点からスタートするときは「出る」だけが起き、ゴールの頂点にたどり着いたときには「入る」だけが起きる。
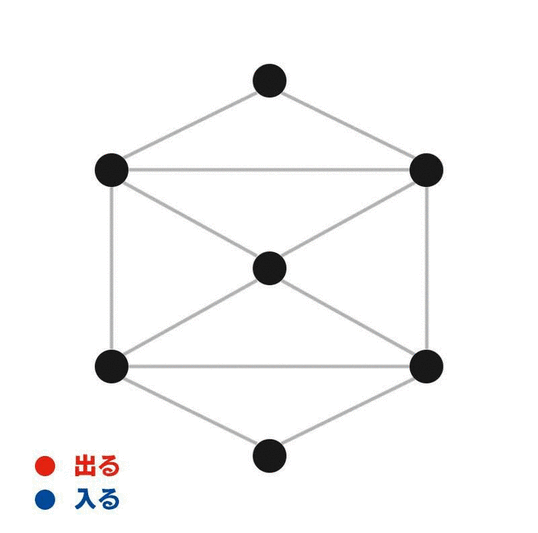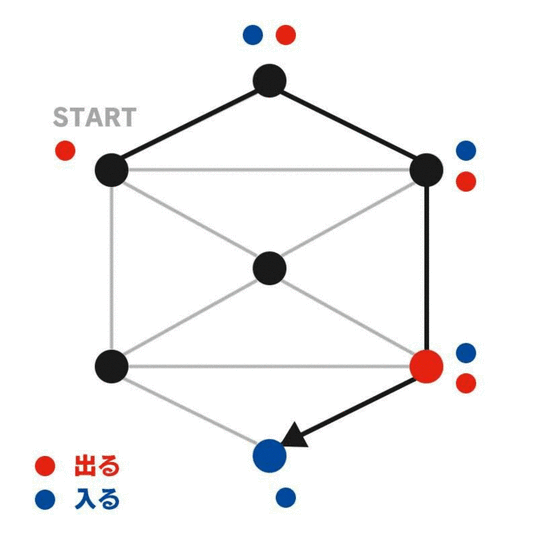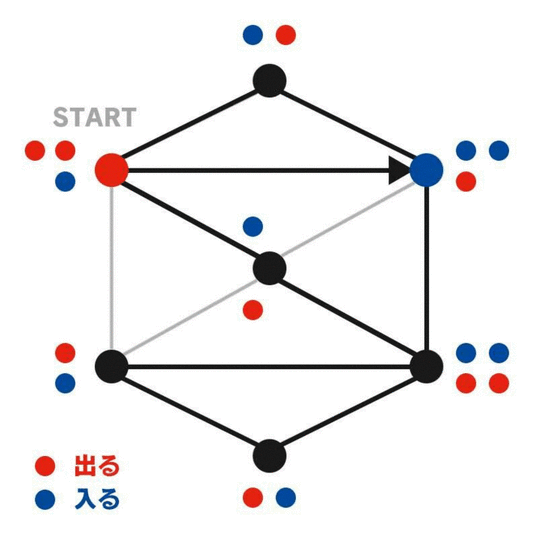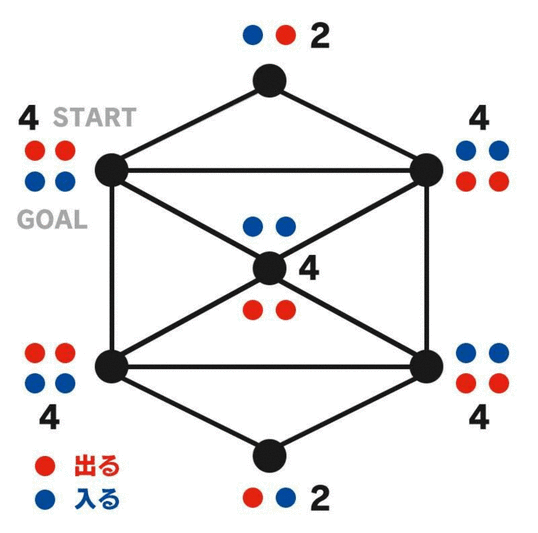
正しい一筆書きのルートをなぞる間に、頂点に「入る」か「出る」たびにその頂点にカウンターを置いていくと、スタートでもゴールでもない頂点は必ず偶数個のカウンターが置かれている。スタートとゴールの頂点に残るカウンターの個数は、それが同じ頂点か違う頂点かによって異なり、
・同じ頂点→その頂点に最初と最後に1個ずつカウンターが置かれるので偶数個 (A)
・違う頂点→それぞれの頂点に最初と最後に1個ずつカウンターが置かれるので両方とも奇数個 (B)
となる。
逆の証明も必要だけど難しい
これで「図形が一筆書きできるならば、頂点に繋がる辺の数が条件を満たす」ことは説明できた。しかしこれでは「頂点に繋がる辺の数が条件を満たしているならば図形が一筆書きできる」ことを保証できない。これを説明するのは上の説明ほど簡単ではないので、概要だけ説明する。
【説明】
辺の数nについての数学的帰納法を用いると証明できる。
・n=1、つまり辺が1本の図形は言うまでもなく一筆書きできる。
・n=kの図形で「頂点に繋がる辺の数が条件を満たしているならば図形が一筆書きできる」と仮定する。
n=k+1の図形がAとBいずれかの条件を満たしているとき、
・Aを満たしているならば、元の図形から辺を1本除くと「n=kのBを満たす図形」になるので、「除いた辺をなぞる→今いる頂点からスタートして、除いた後の図形を一筆書きする」で一筆書き可能。
・Bを満たしているならば、奇数辺の頂点が2つ（PとQ）ある。「Pから出ている辺」の1本を除いて「n=kの図形」にする。その辺がQと繋がっているか、辺を除いたことで図形がバラバラにならないか……などの場合分けはあるが、結局のところ残った図形も条件を満たすので一筆書き可能。
よって数学的帰納法により「条件を満たす図形は必ず一筆書きできる」ことが分かる。
説明が長くなってしまったが、一筆書きの攻略法をまとめよう。目指せトップアスリート！
- 各頂点の繋がっている辺の数を数えて、条件A（すべて偶数）とB（2つだけ奇数）のどちらが満たされているか調べる。どちらでもないなら一筆書き不可能。
- 条件Aの図形ならばどこから始めても一筆書きできる。
- 条件Bの図形ならば、奇数辺の頂点から始めると、もう一方の奇数辺の頂点に戻るような一筆書きができる。
なお、このような問題を扱うのは「グラフ理論」という学問であり、この記事で一貫して「図形」と呼んでいたものは「グラフ」として扱われる。一筆書きのより正確で詳細な説明が知りたいならばグラフ理論の本を読んでみてほしい（どの本でも必ずといっていいほど取り上げられているはず）。
