コジマです。
先日、有理数とは何か?という記事を書いた。すごくざっくり説明すると「分数で表せる数は有理数」である。
桁の数が有限個である「有限小数」や、無限個であっても同じ数字の並びが繰り返される「循環小数」はすべて分数で表せる有理数である、という話だった。
ところで小数といえばこんな話がある。
0.999…=1
つまり、小数第1位から9が連続する0.999…という小数は、完全に、偽りなく、寸分違わず1と等しい。
この事実を初めて知って「そんな訳ないじゃん」と思っているあなた。あるいはこの話を知っているが未だにピンときていないあなた。今からの説明で何とか納得していただきたい。
分数に変形すれば……
上に書いた通り、すべての循環小数は分数で表せる。0.999…も分数に変形してみよう。
a=0.999… (1)
とすると、10a=9.999… (2)。
(2) から (1) を引くと9a=9となって、a=9/9=1。つまり0.999…=1だ!
実は説明できてない?
このような説明は小学校や中学校でもよくなされるのだが、実はちょっと怪しい面がある。
皆さんは「無限小数を対象にした計算」の方法を習った記憶があるだろうか。例えば0.5454…×4みたいな。
もしかしたら、0.5454…を分数に直してから4をかける、と習うことはあるかもしれないが、0.5454…をそのまま4で掛ける方法というのは習っていないはずである。
要するに、すごく厳密なことを言うと0.999…×10は小学校や中学校で習った範囲では計算できないのだ(とはいえ、0.999…×10の場合に限れば間違った結果にはならないので簡潔な説明のために使うのは悪くない)。
ではどうするのかというと、高校数学で習う無限級数という概念を用いる。ただ、具体的な計算方法にまで踏み込むと難しくなるので、ここでは図を使って直感的に説明しようと思う。
無限に近付いていく
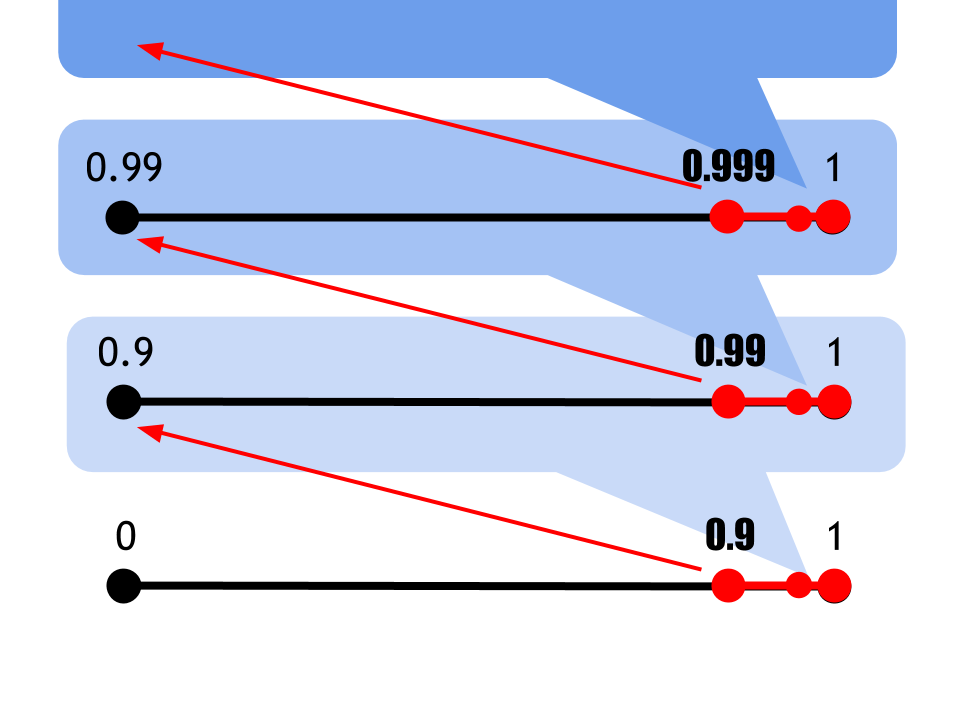
数直線上の0と1の間を9:1に内分する点は0.9である。
さらに、0.9と1の間を9:1に内分する点は0.99である。
さらにさらに、0.99と1の間を9:1に内分する点は0.999である。
0.999…というのは小数点以下に9が無限に続く数字だから、この操作を無限回繰り返したときに得られる点が示す数字と一致する。
9:1の内分を無限に繰り返すと、0.999…9と1の距離は無限に小さくなるので、極限の考え方の上では0.999…と1は同じ数なのだ。
どうだろう、納得していただけただろうか。
無限の概念は無限に考えても腑に落ちないかもしれない。無限に難しいな。








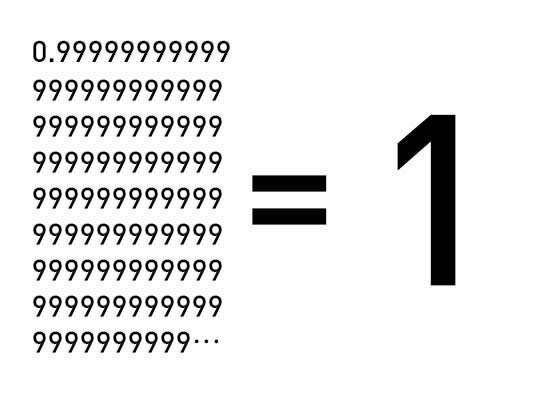

.jpg)

















