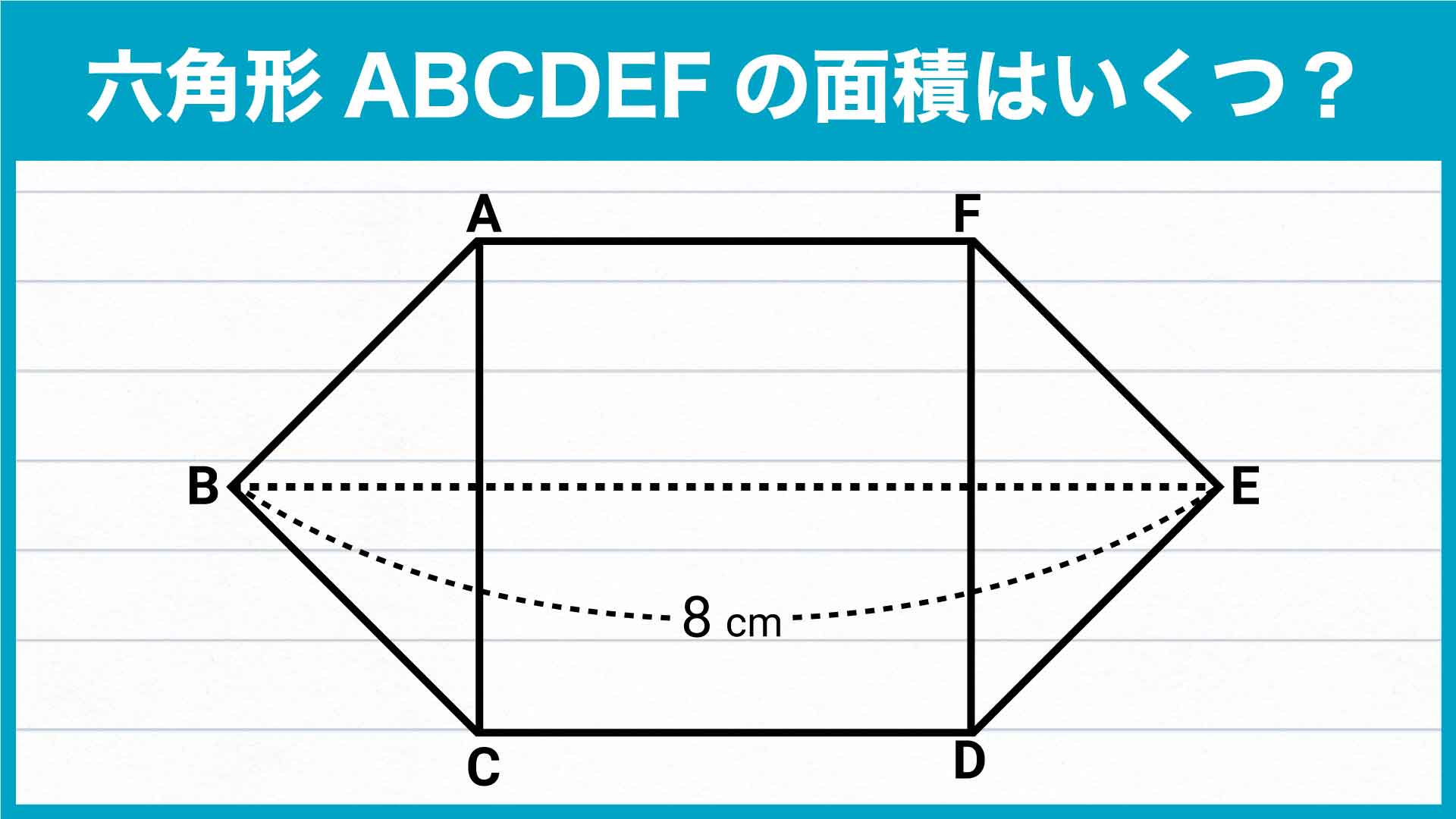
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解法のポイントは「補助線を2本引いて、中心の正方形を分割する」ことです。
補助線を引くと、解き方の道筋が見えてきます。
補助線2本、どこに引く?
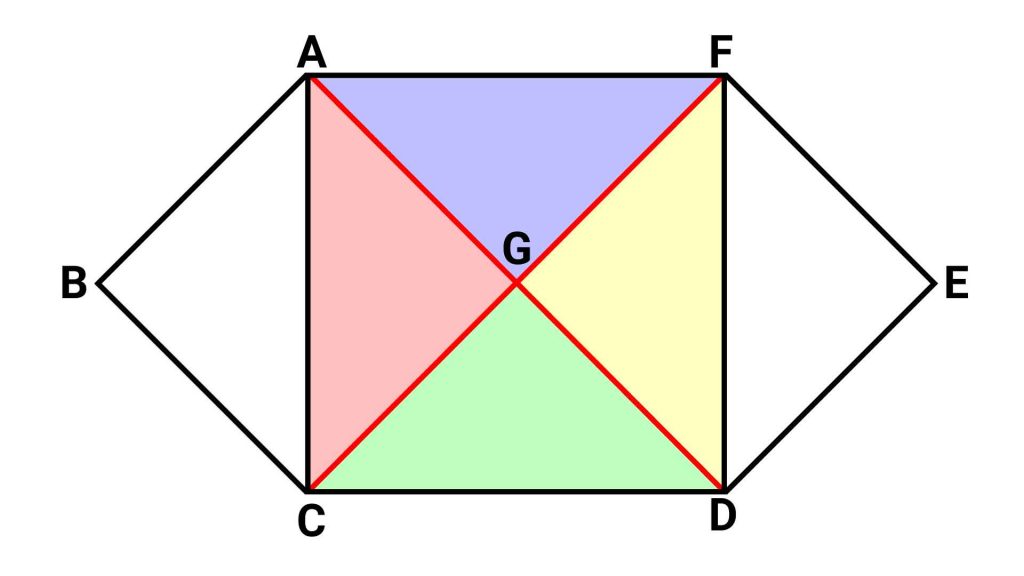
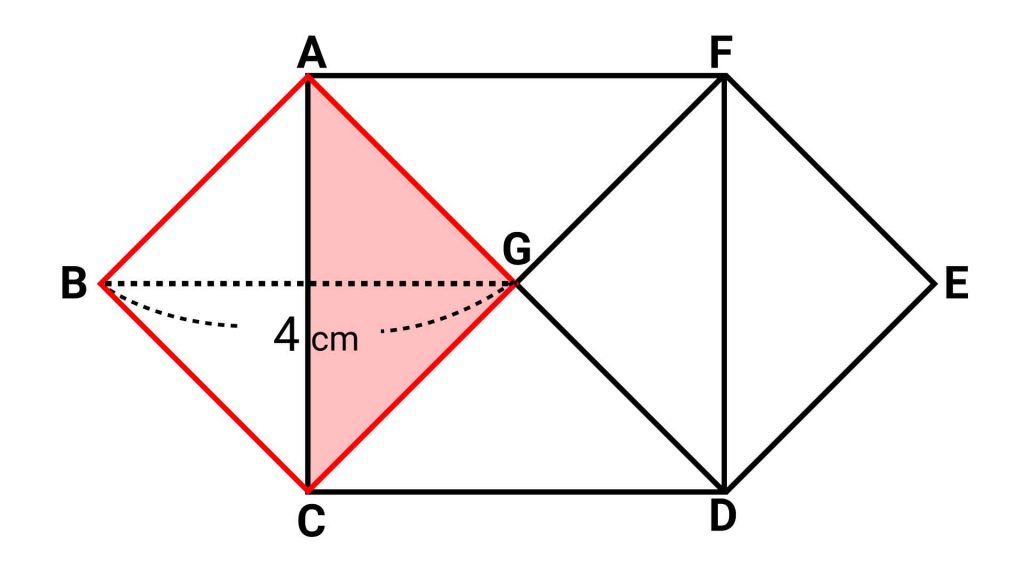
引くべき2本の補助線は、下の図で赤線で示している2本です。ちょうど、正方形ACDFの対角線にあたります。
対角線を引くことで、正方形ACDFを面積が等しい4つの直角二等辺三角形に分割することができます(正方形の2本の対角線は同じ長さで、中点で垂直に交わるため)。
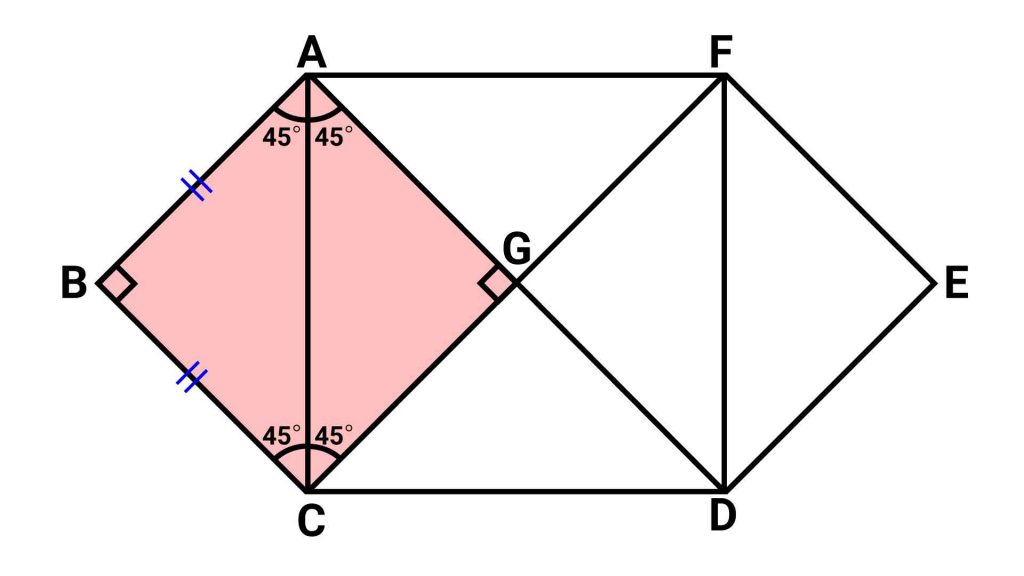
ここで、四角形ABCGについて考えます。四角形ABCGは、下の図に示すように全ての内角が90度であり、かつ三角形ABCは二等辺三角形であることからBA=BCなので正方形となります。
つまり正方形ABCGにおいて、対角線ACによって分けられている三角形ABCと三角形AGCは同じ形であるといえます。
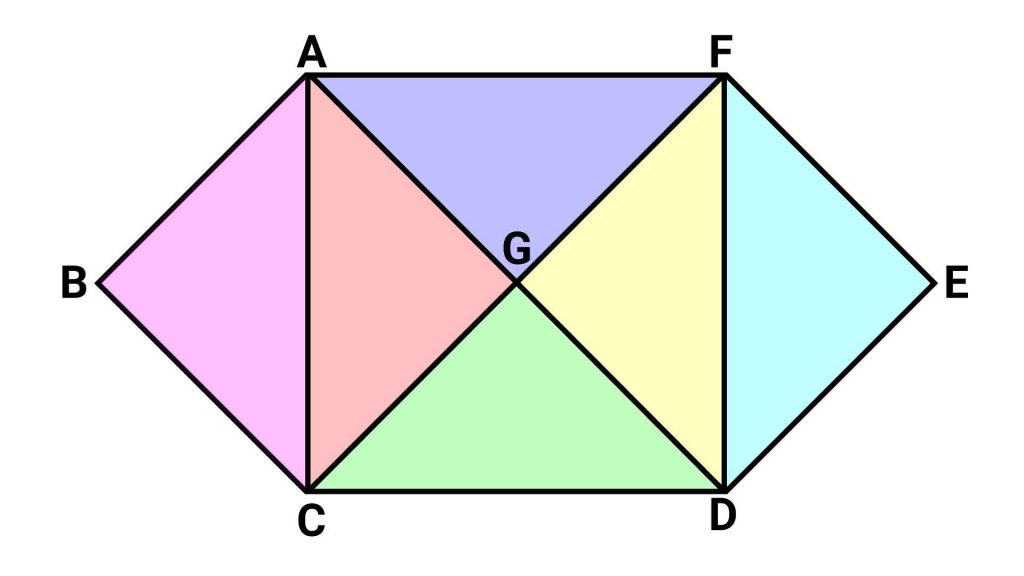
これは四角形FGDEについても成り立つため、六角形ABCDEFは、面積が等しい6つの直角二等辺三角形で成り立っていることがわかります。
これらのことから、1つの直角二等辺三角形の面積を求めて6倍すれば、六角形ABCDEFの面積を求めることができます。
1つの直角二等辺三角形の面積は?
ここでは、三角形AGCの面積を求めていきます。
四角形ABCGは正方形で、GはBEの中点であることから、正方形ABCGの対角線の長さは8÷2=4cmです。
正方形の面積は、ひし形の面積を求める式「(対角線)×(対角線)÷2」で計算できるので、正方形ABCGの面積は4×4÷2=8cm2です。
また、三角形AGCは正方形ABCGの半分なので、三角形AGCの面積は8÷2=4cm2です。
したがって、六角形ABCDEFの面積は1つの三角形の面積を6倍すればよいので、4×6=24cm2となります。
答え:24cm2
六角形を分割できるかがキーとなる問題でした。
それでは。
【あわせて読みたい】










.jpg)








.jpg)






