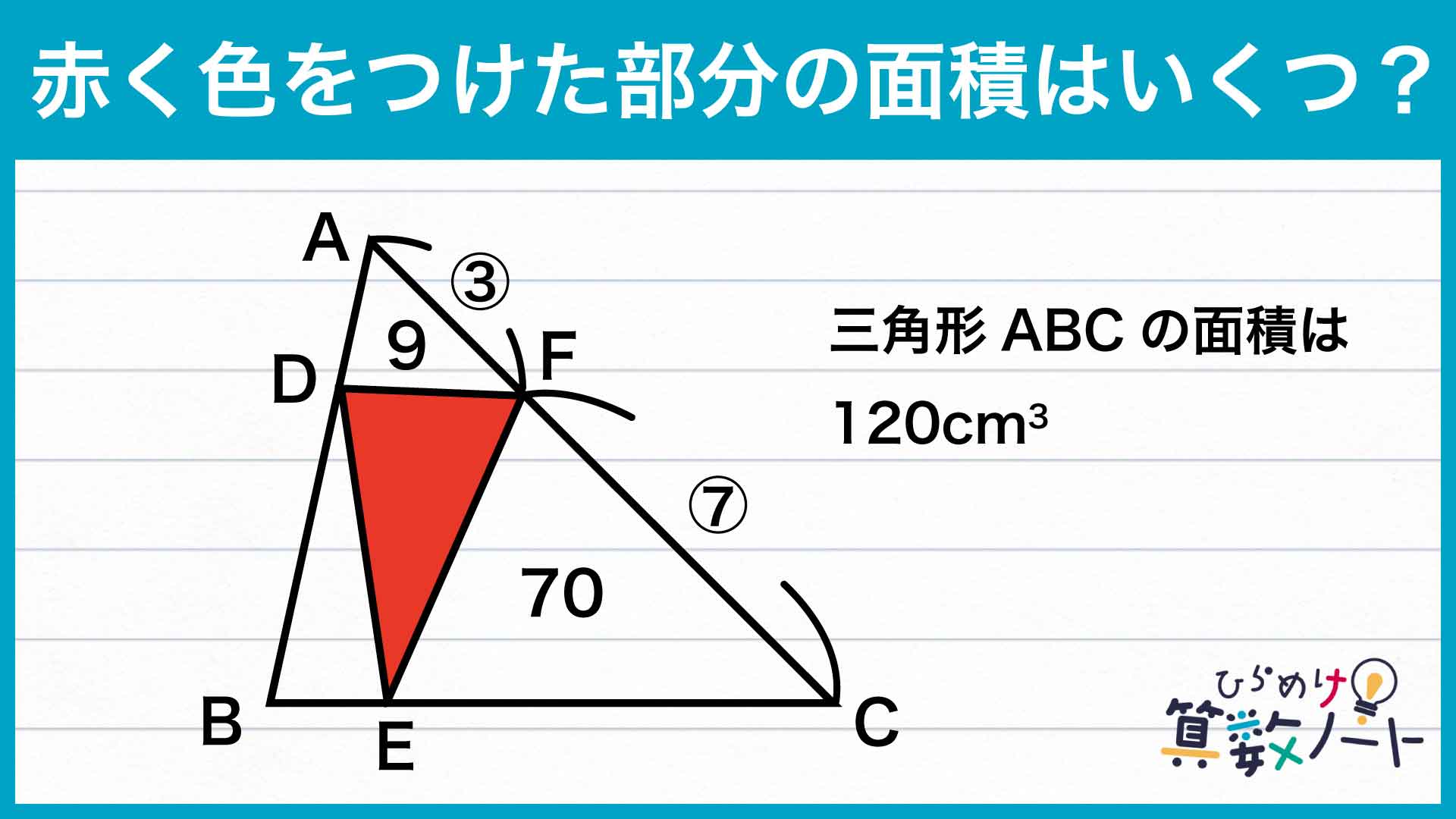
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
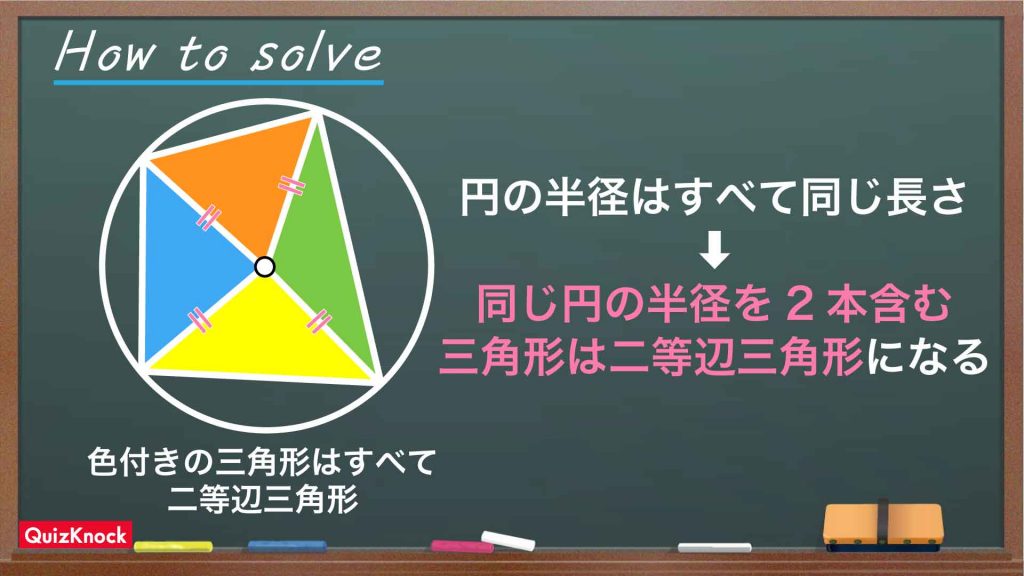
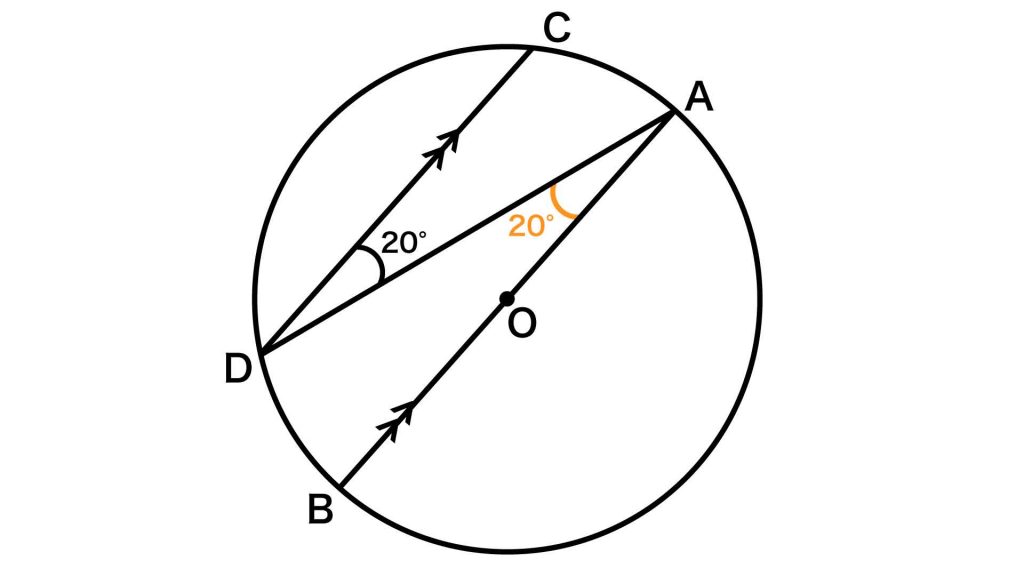
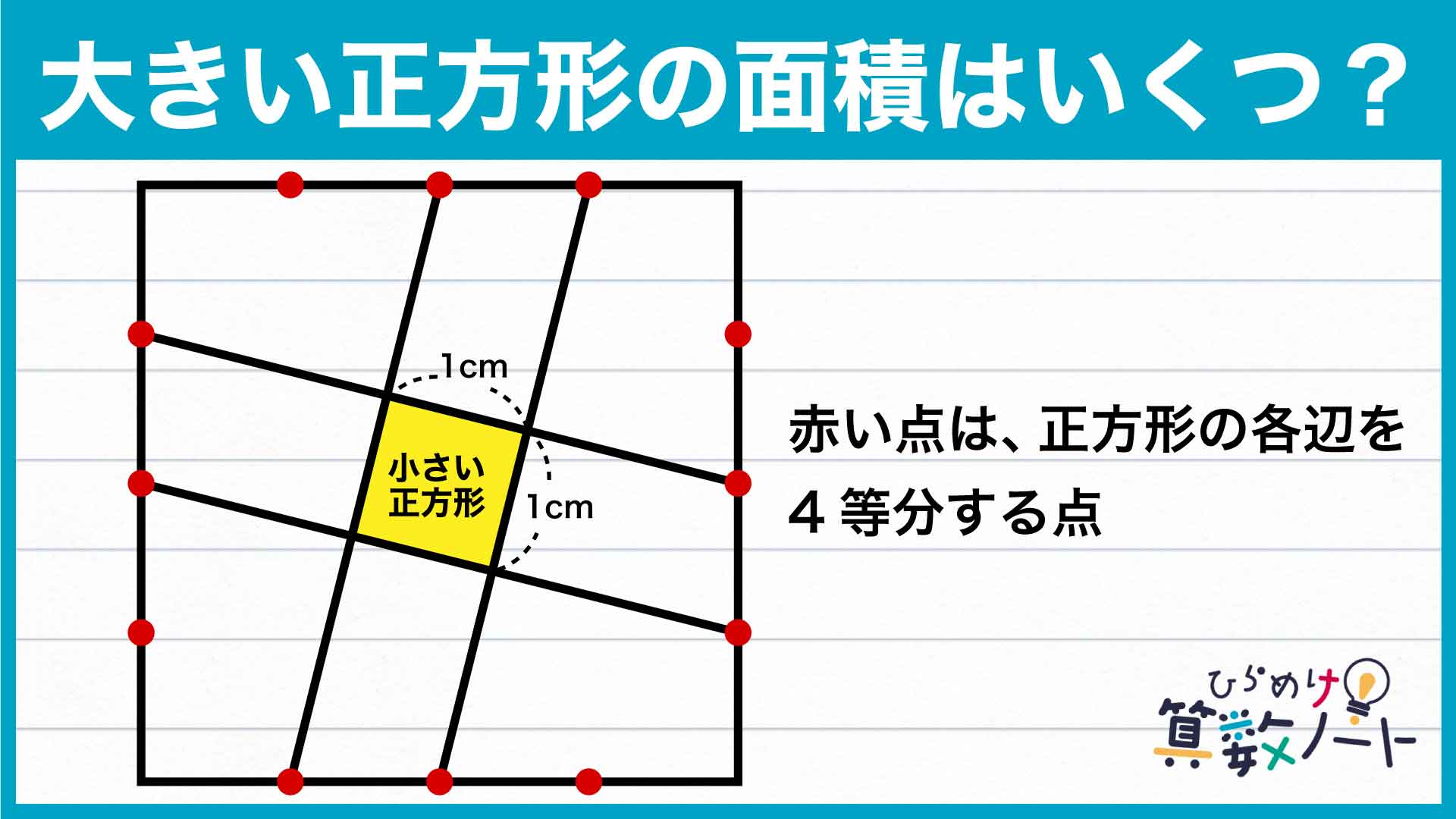
この問題を解くうえで重要なポイントをまとめた図がこちらです。
ポイントは「円の半径に着目し、二等辺三角形を見つける」ことです。
このことを意識して、解いていきましょう!
平行線に注目する
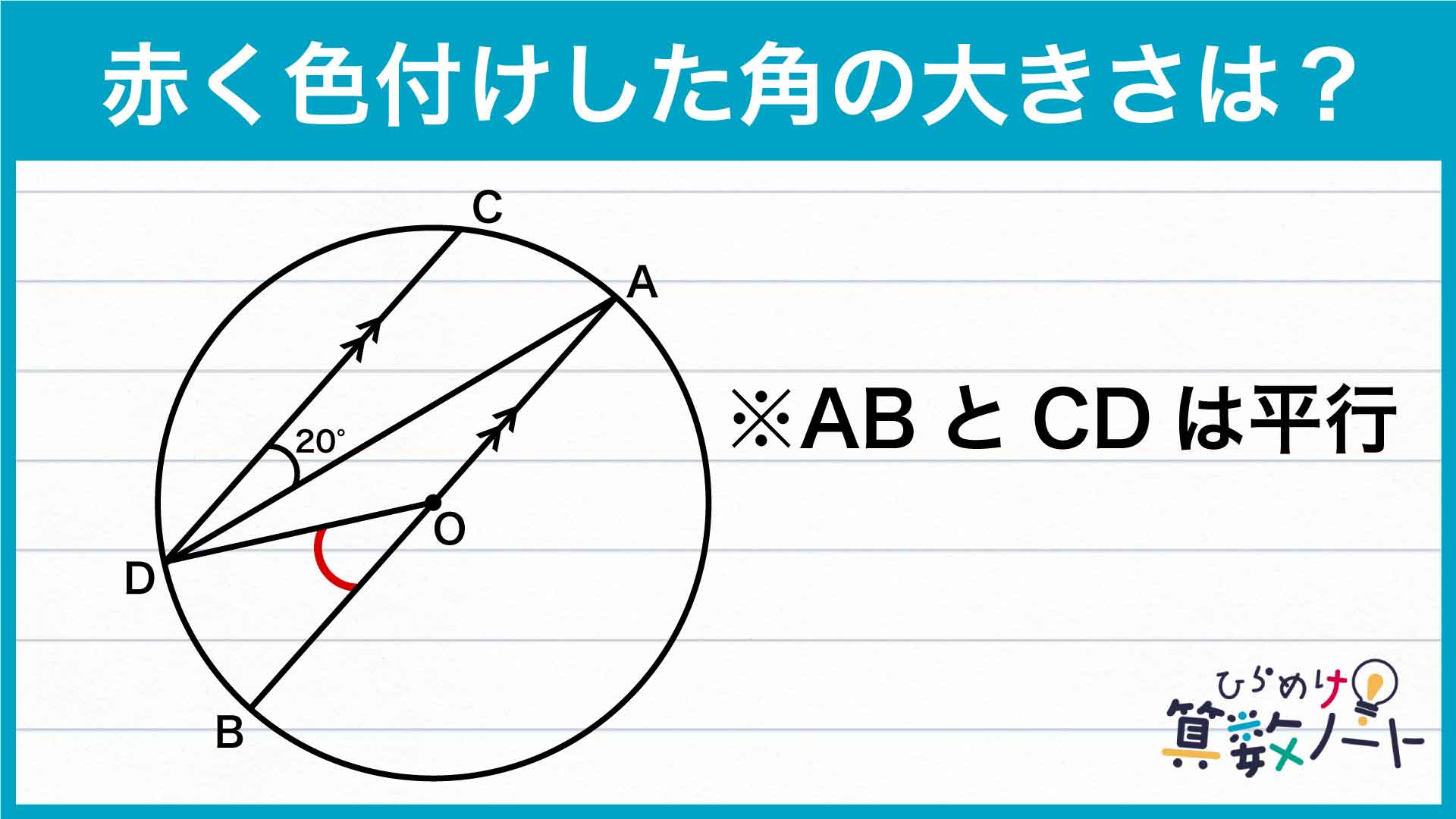
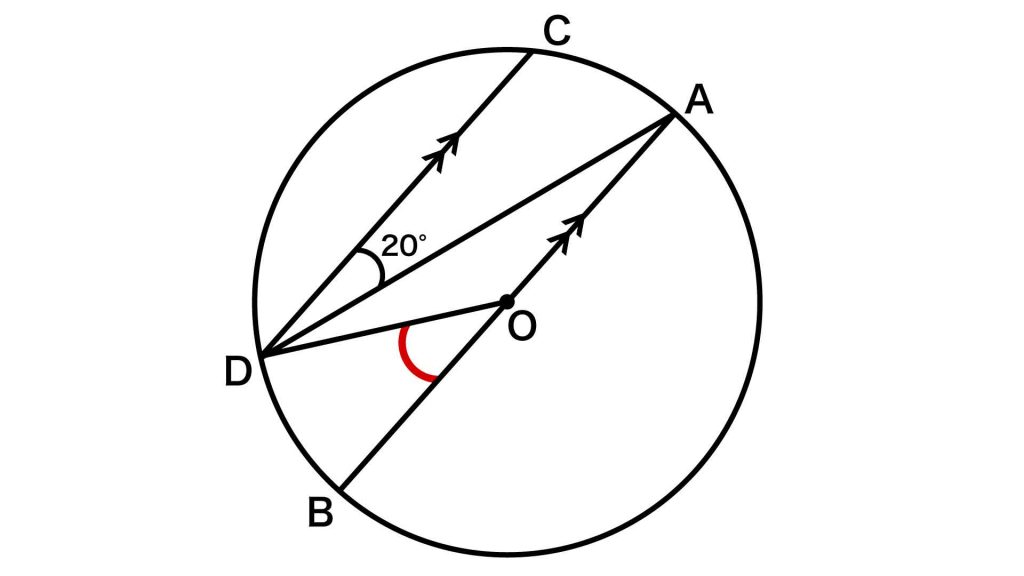
まず、平行な2本の線分ABと線分CDに注目しましょう。平行線の錯角は同じ大きさとなるので、角CDA=角DAB=20度です。
二等辺三角形を見つける
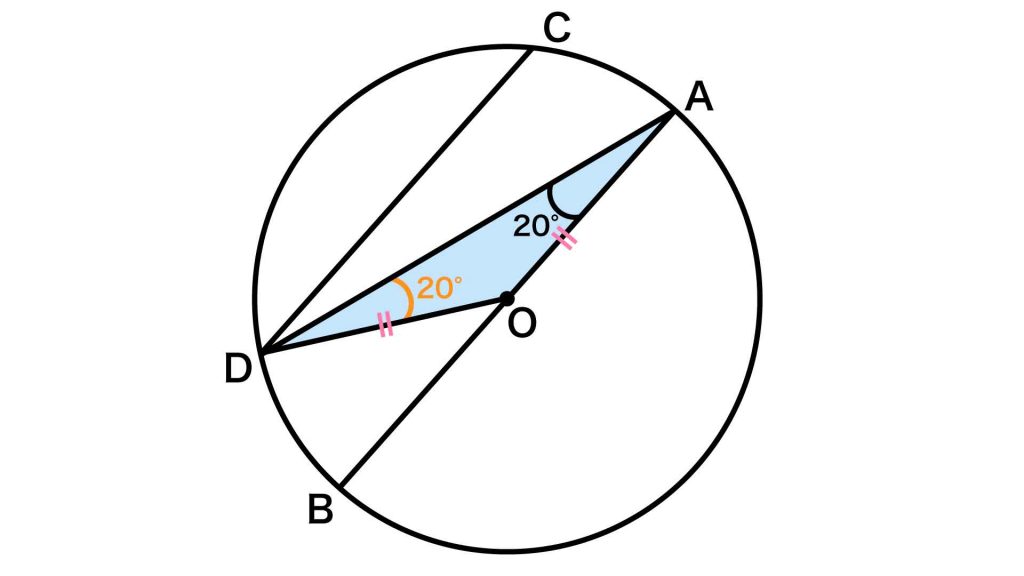
先に述べたように、同じ円の半径を2本含む三角形は二等辺三角形となります。
三角形ODAに注目すると、OAとODは円の半径なので長さは等しくなります。よって、三角形OADは二等辺三角形となり、角OAD=角ODAとわかります。したがって、角ODAの大きさも20度となります。
あと少し!
ここまでで、三角形ODAの内角のうち、2つの角の大きさを求めました。
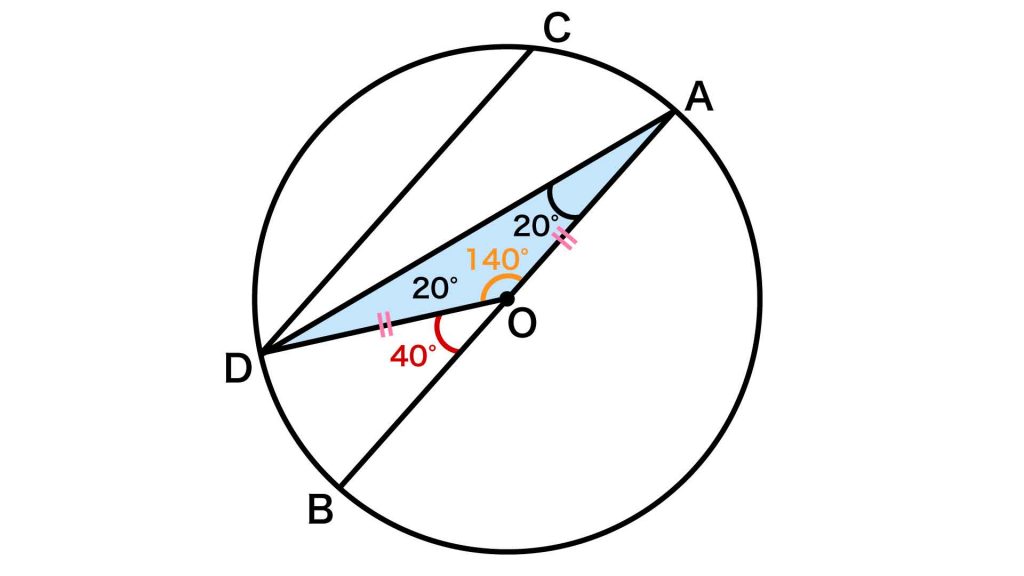
三角形の内角の和は180度なので、角ODA+角OAD+角AOD=180度が成り立ちます。
以上より、角AODの大きさは、180-20-20=140度です。したがって求める角BODの大きさは、180-140=40度となります。
答え:40°
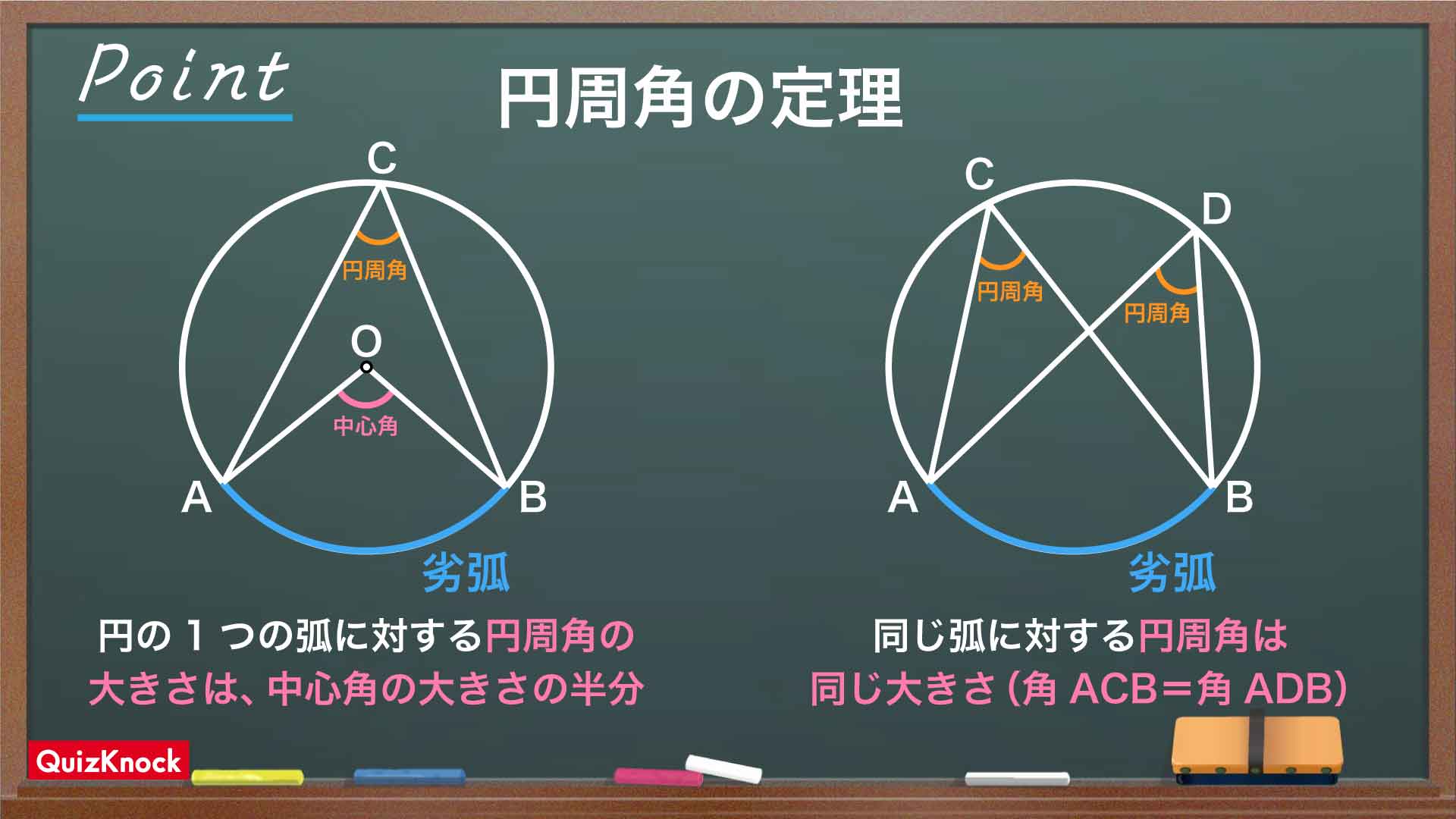
中学校で習う「円周角の定理」を使えばもっと簡単に!
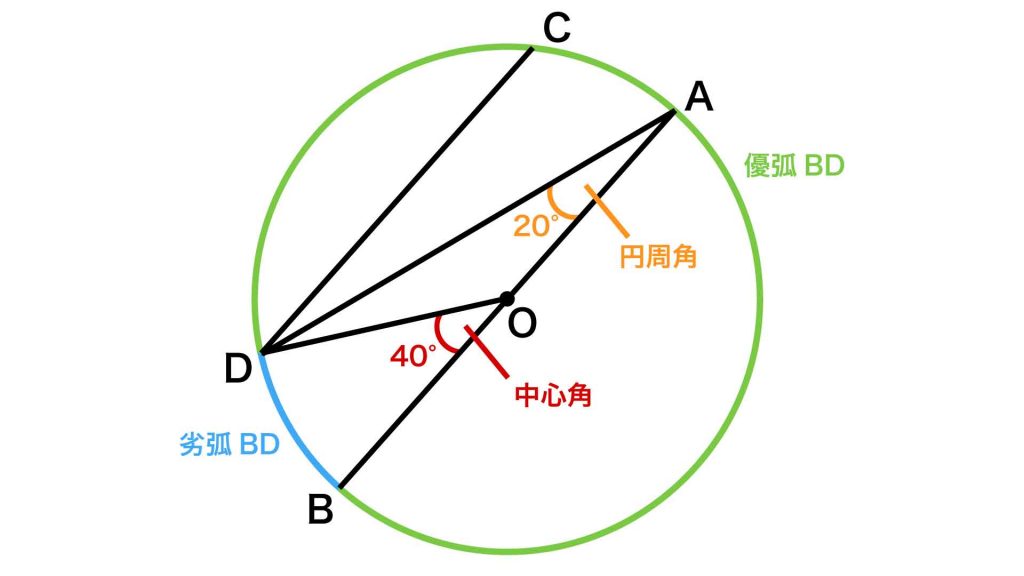
先ほどの図に登場した角について、中学数学では、角DABを「劣弧BDに対する円周角」、角BODを「劣弧BDに対する中心角」と表現します。「劣弧」とは、円周を2つの点によって2つの曲線(弧)に分けたときの短い方の弧を指します(長い方は「優弧」といいます)。
そして、解説で角DAB(円周角)の大きさが20度、角BOD(中心角)の大きさが40度であることを求めましたが、同じ弧に対する円周角の大きさは、必ず中心角の大きさの半分になります。この性質は点Aが優弧BD上(点B、D上を除く)のどこにあっても成り立ち、これを「円周角の定理」といいます。
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)









.jpg)