小学5年生で解ける「面積の問題」、あなたは解ける？【祝・第50回】

解説

それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです。

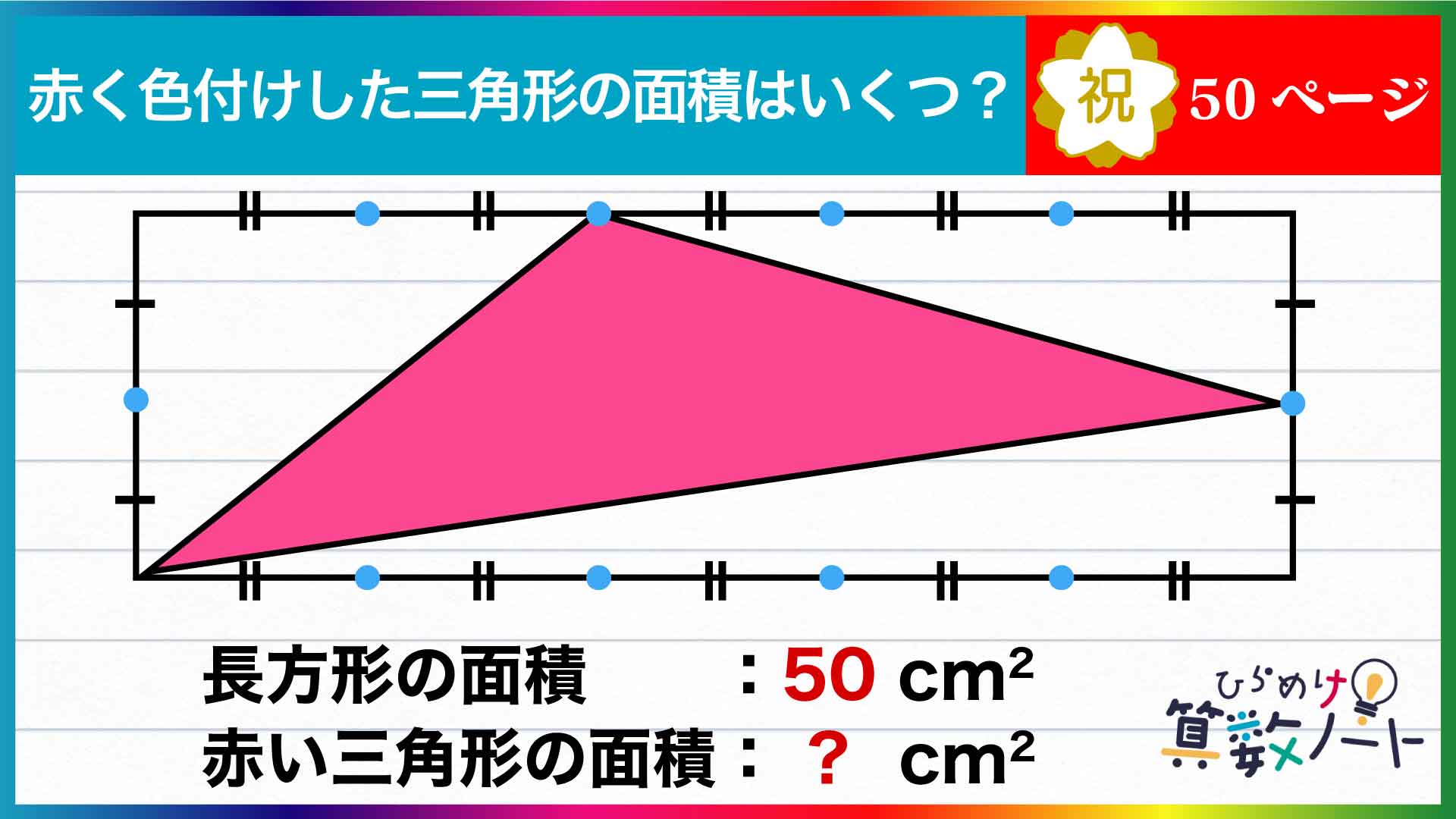
赤い三角形の3辺の長さがわからないため、三角形の面積の公式を使って求めるのは難しそうです。

そこで、「長方形の面積が50cm²である」という情報を使って求めることを考えます。

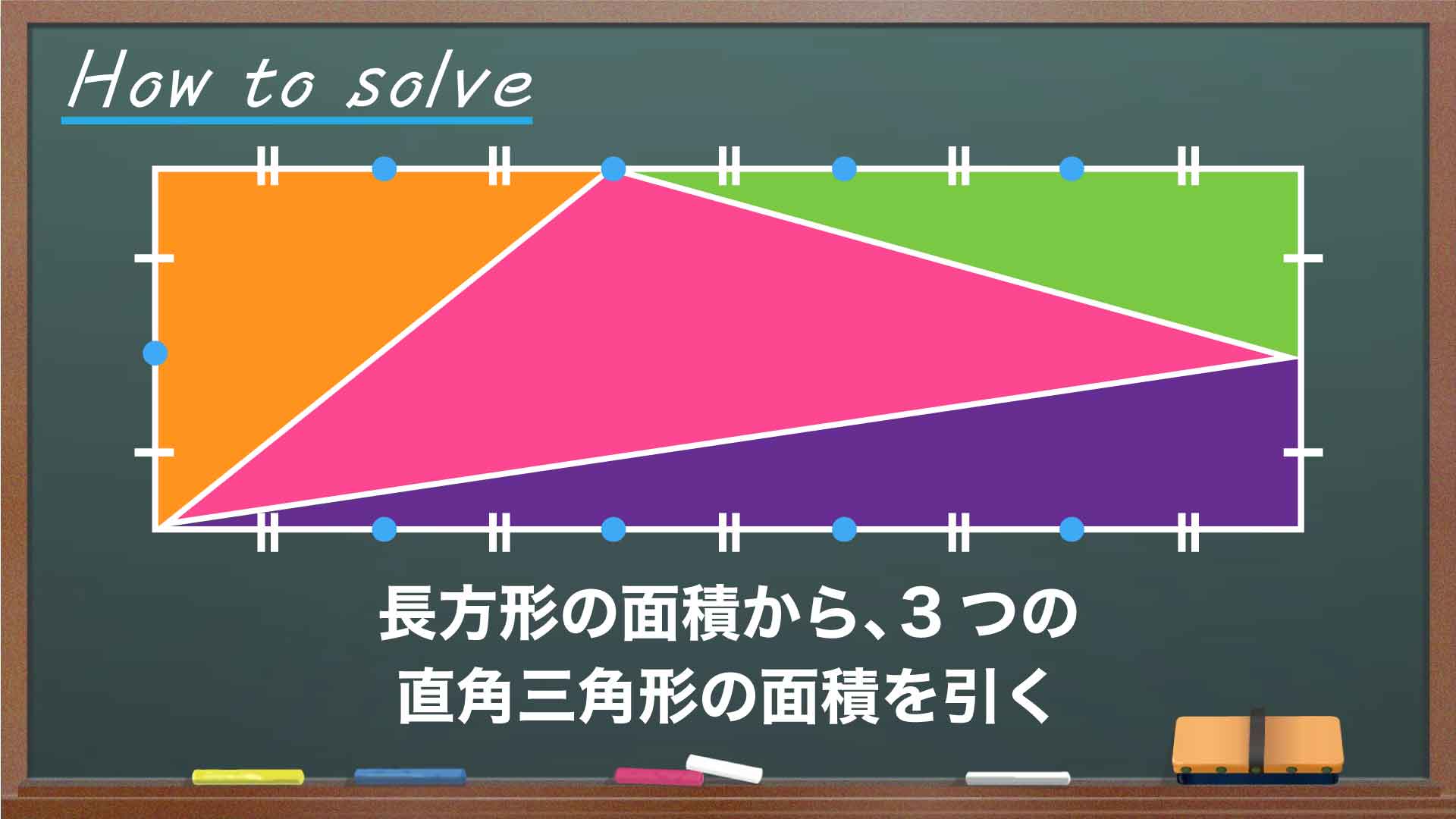
長方形の面積から、以下の図で示した3つの直角三角形の面積を引けば、赤い三角形の面積を求めることができます。

では、3つの直角三角形の面積を求めるにはどうすればいいのでしょうか？

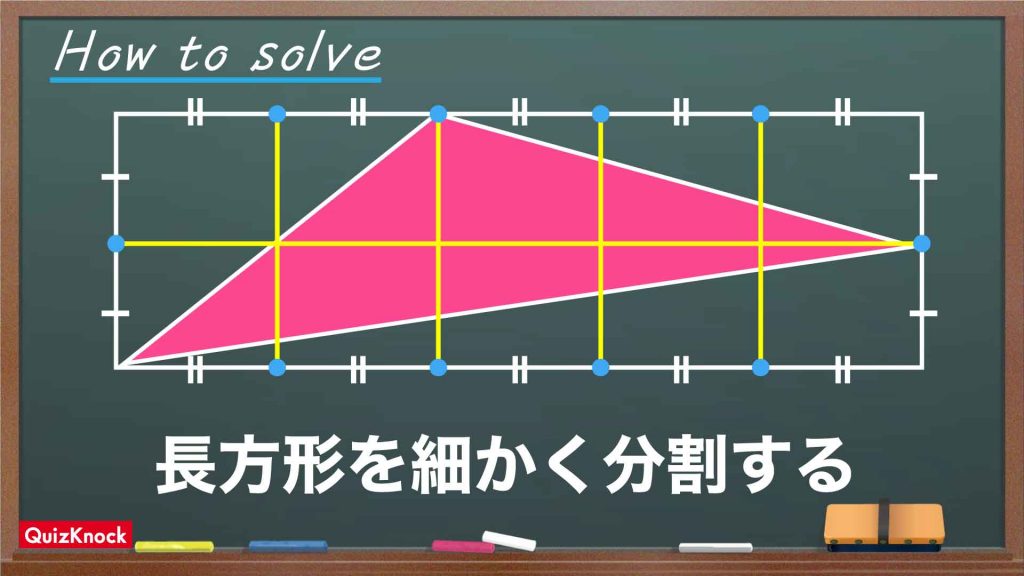
ここで重要になるのが「補助線」です。今回の問題では補助線を5本引き、大きな長方形を小さな長方形に分割します。

こうすることで、3つの直角三角形の面積を求めることができます。

以上のポイントを踏まえ、問題を解いていきましょう。

補助線を引く

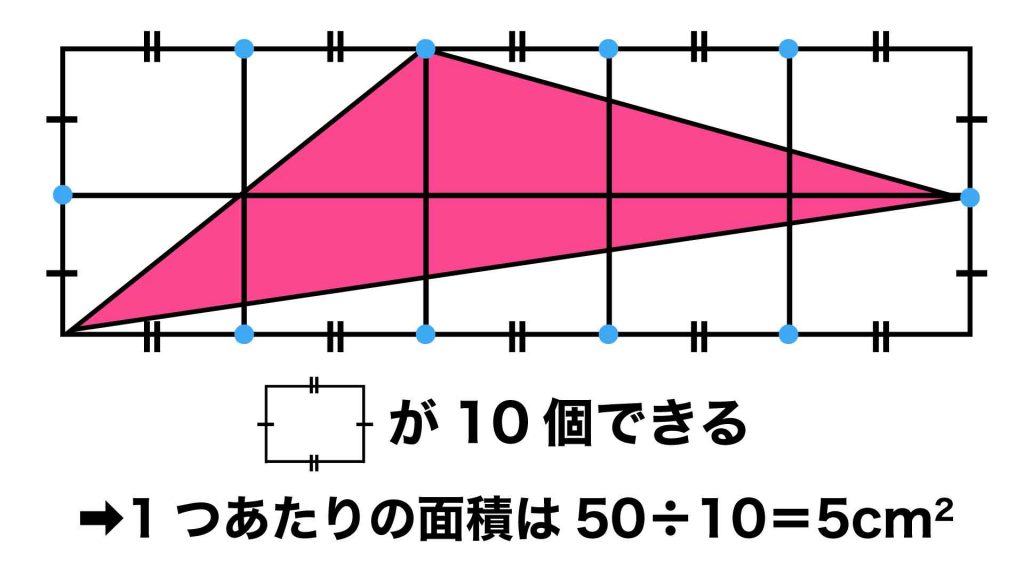
まずは、以下の図のように補助線を引き、大きい長方形を分割します。

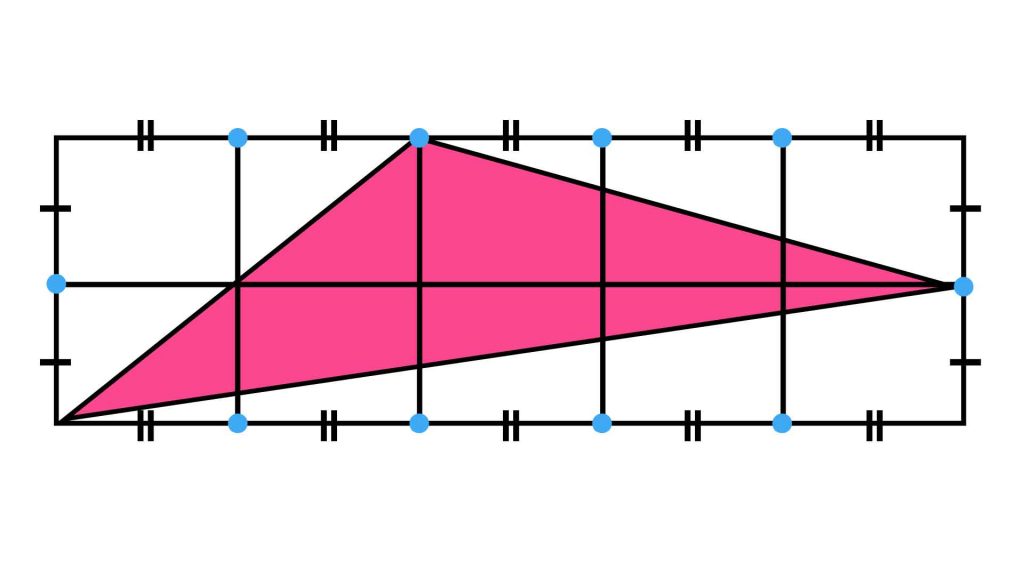
補助線を引いたことにより、大きな長方形を小さな長方形10個に分割することができました。

これらの小さな長方形は、縦の長さ、横の長さがそれぞれ全て等しくなるため、面積も全て等しくなります。

したがって、長方形1つ分の面積は、50÷10=5cm²となります。

直角三角形の面積を求める

ここからは、3つの直角三角形の面積を求めていきます。

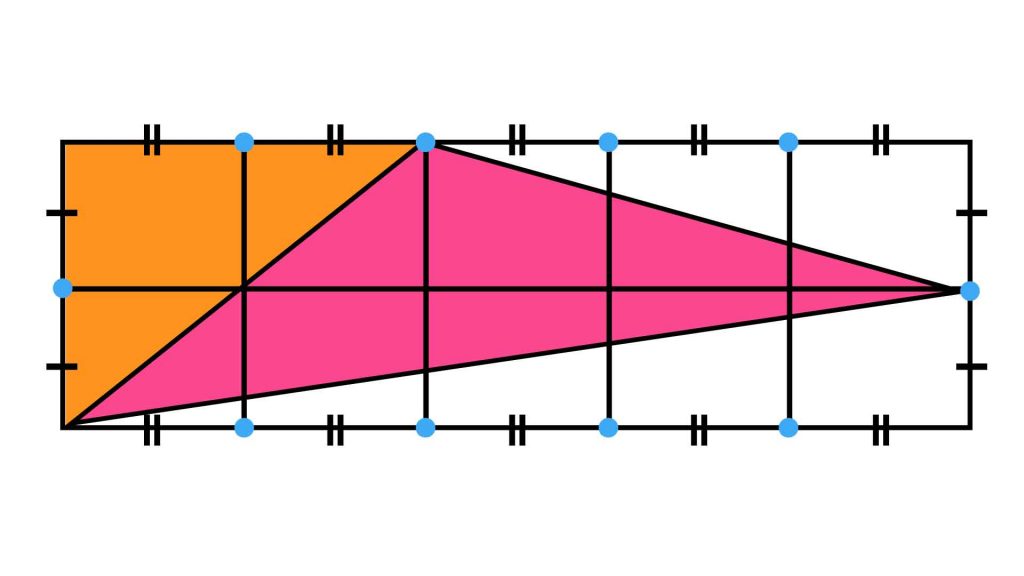
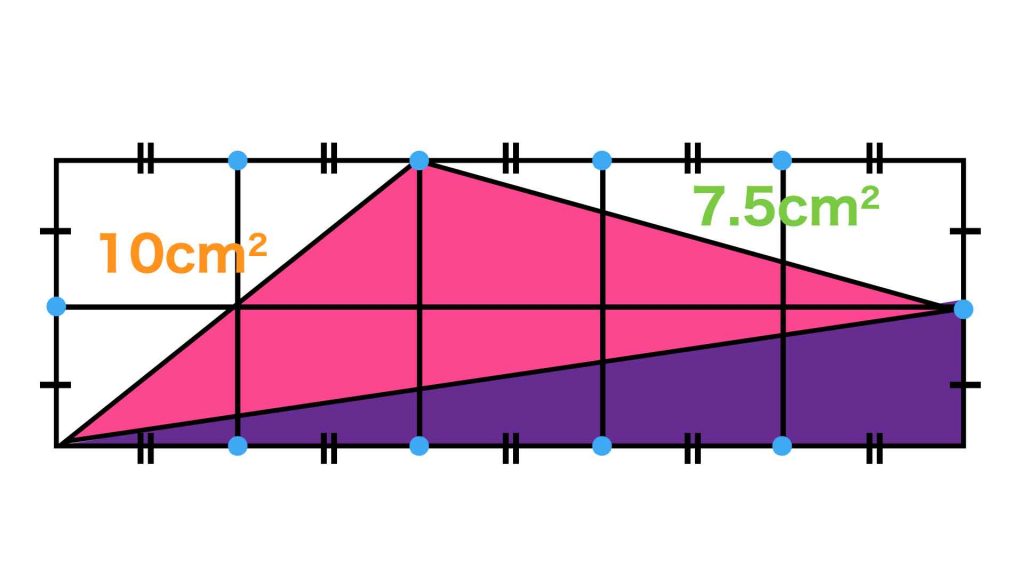
まずは、以下の図でオレンジ色で示した直角三角形です。

この直角三角形の斜辺は、小さい長方形が4つ組み合わさってできる長方形の対角線となっています。

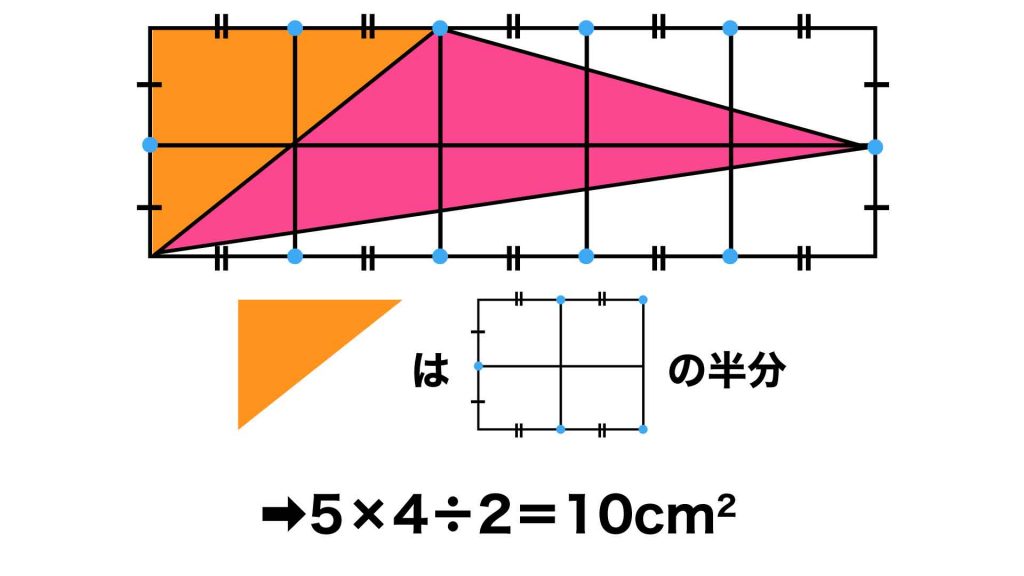
したがって直角三角形の面積は、この長方形の面積のちょうど半分となります。

長方形の面積は、小さい長方形4つ分なので5×4=20cm²です。したがってオレンジの直角三角形の面積は、20÷2=10cm²となります。

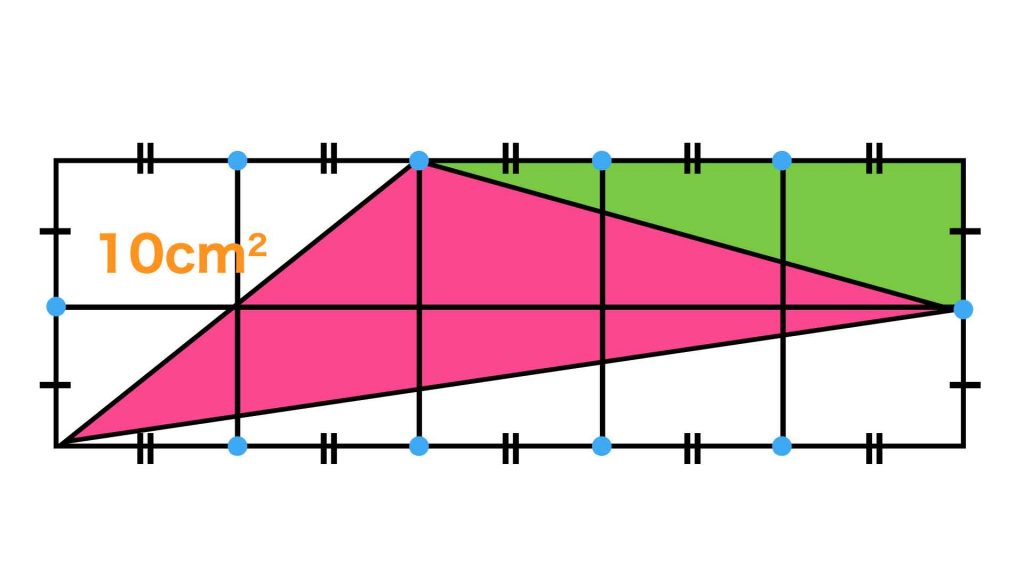
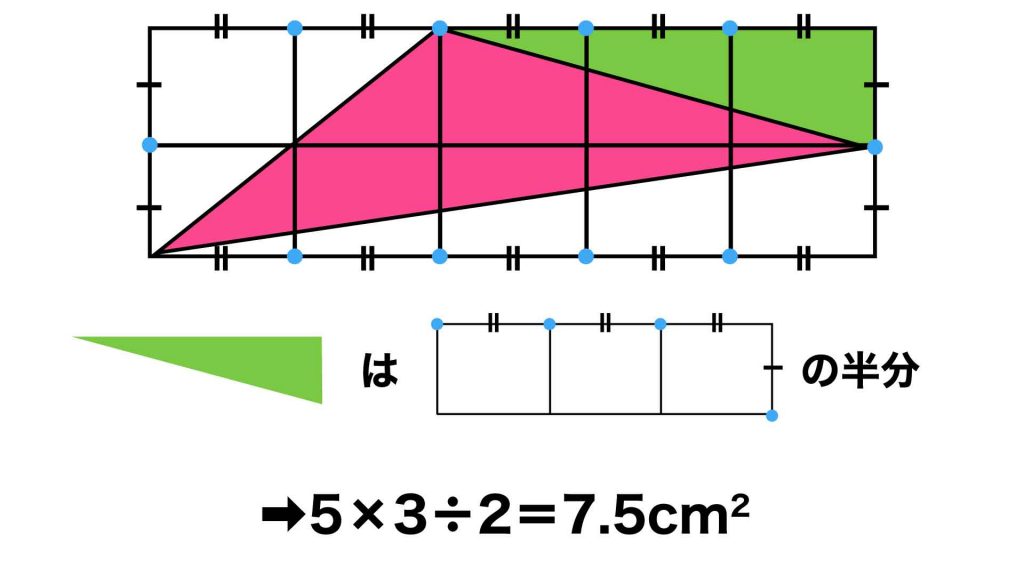
次に、以下の図で緑色で示した直角三角形です。

先ほどと同様に考えると、この直角三角形の面積は、小さい長方形が3つ組み合わさってできる長方形の面積のちょうど半分となります。

したがって緑色の直角三角形の面積は、5×3÷2=7.5cm²となります。

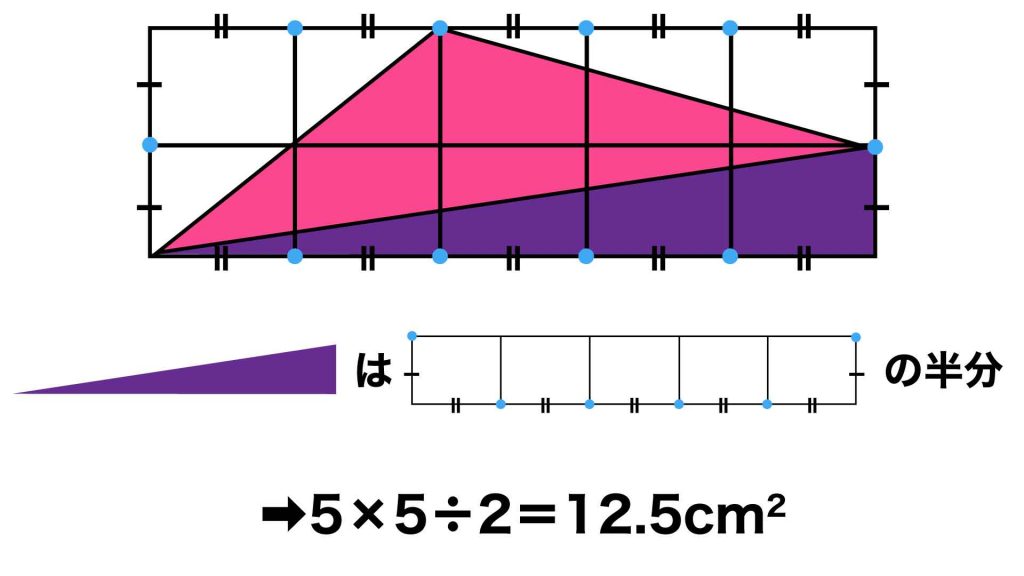
最後に、以下の図で紫色で示した直角三角形です。

この直角三角形の面積は、小さい長方形が5つ組み合わさってできる、横長の長方形の面積のちょうど半分です。

したがって紫色の直角三角形の面積は、5×5÷2=12.5cm²となります。

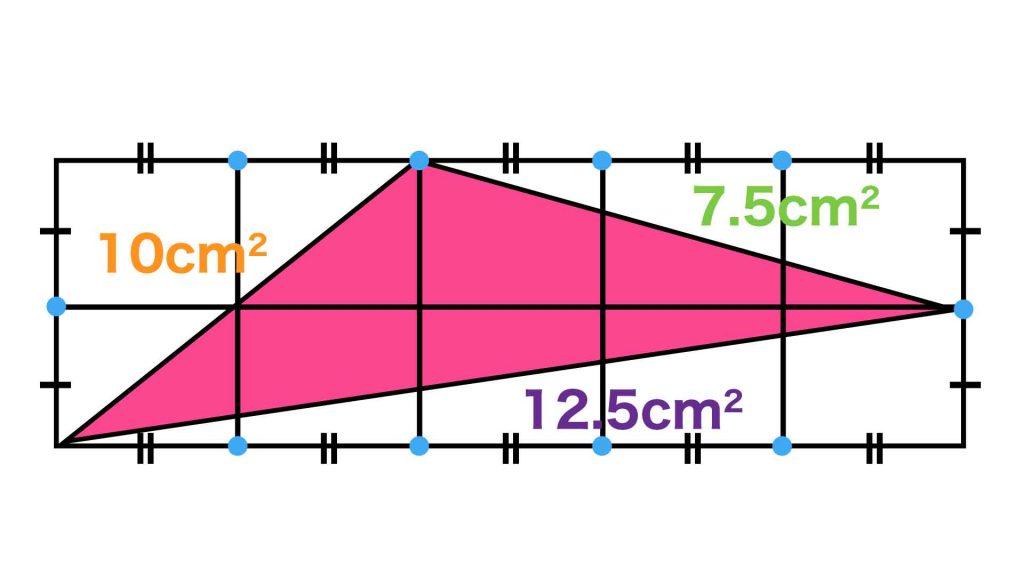
赤い三角形の面積を求める

赤い三角形の面積は、長方形の面積から、3つの直角三角形の面積を引くことで求められます。

長方形の面積は50cm²なので、赤い三角形の面積は、50-(10+7.5+12.5)=20cm²となります。

答え：20cm²

「ひらめけ！算数ノート」は、読者の皆さんの算数愛のおかげで、50ページ目まで続けることができました。

ページはこれからも書き加え続けますので、ぜひチャレンジしてください！

それでは。

【前回の算数ノートはこちら】

【あわせて読みたい】