解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ!以下は解答の答えです
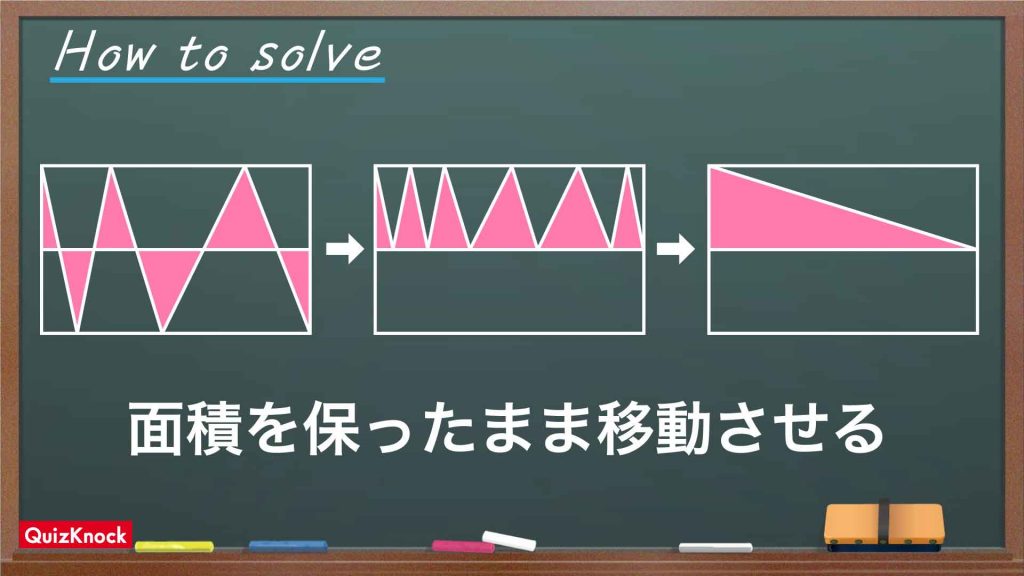
今回のポイントは、「三角形を変形させて、1つの三角形にする」ことです。
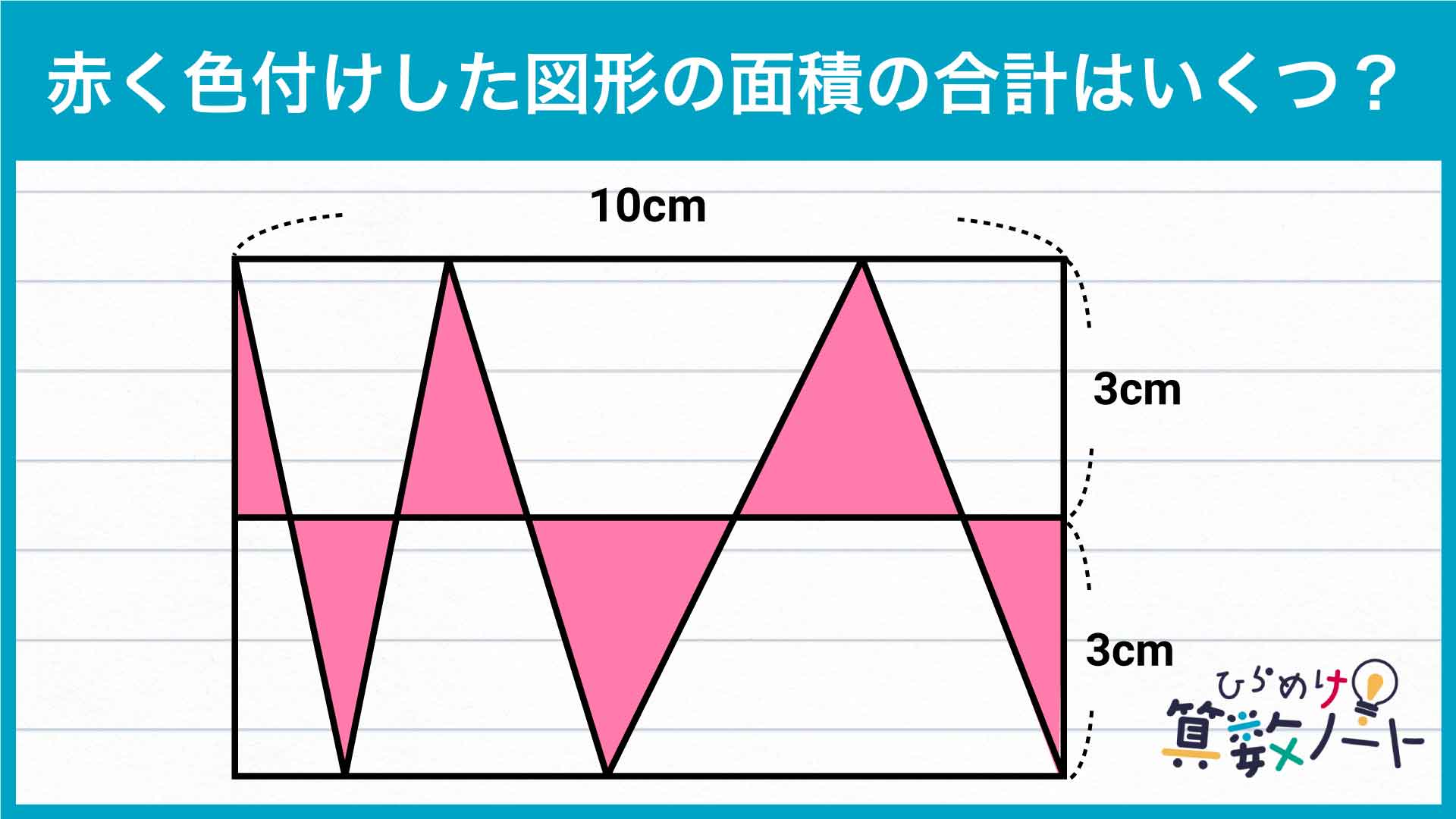
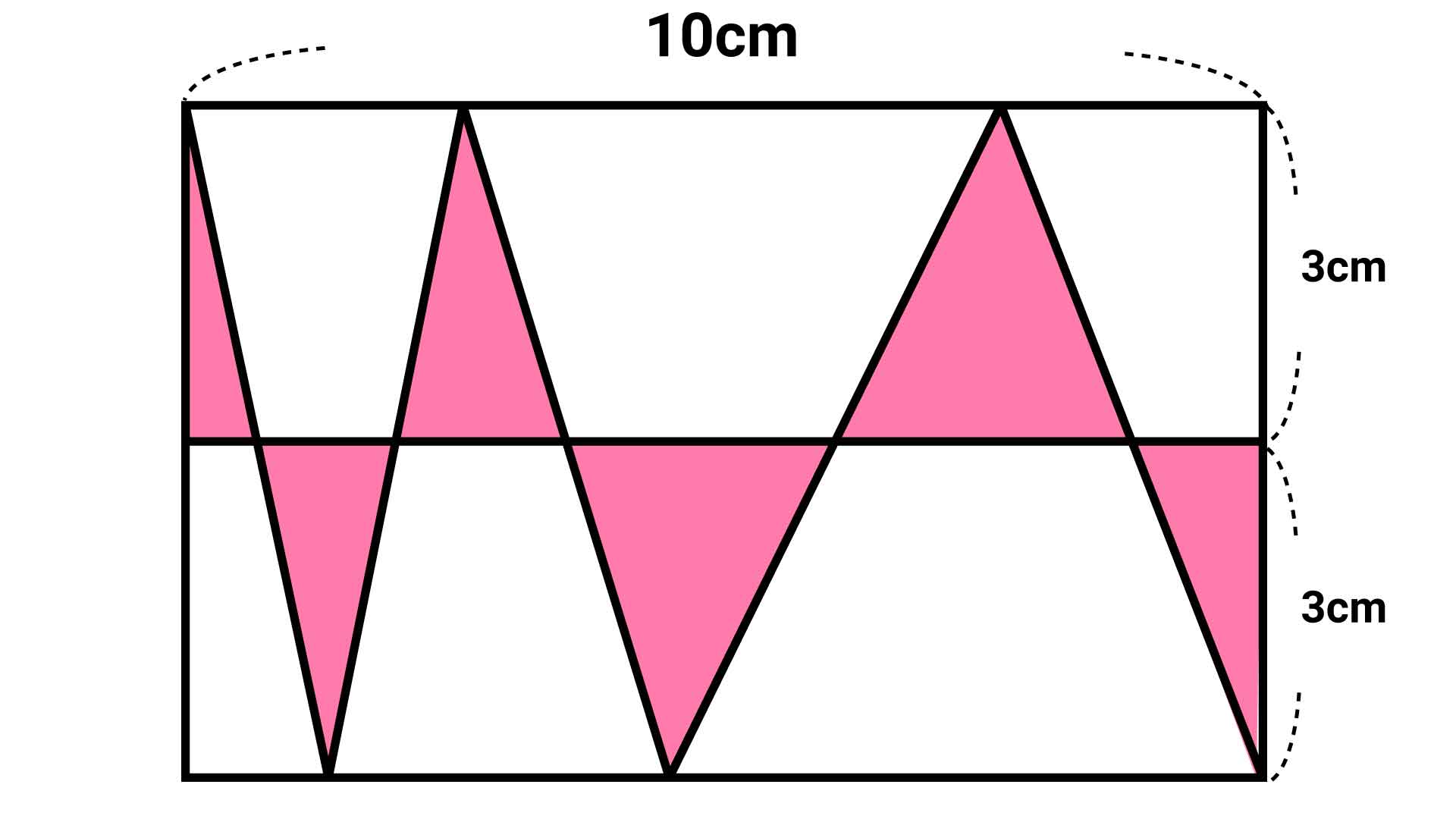
三角形の面積を求める公式は「底辺×高さ÷2」であり、高さは3cmなので、底辺の長さがわかれば面積を求められます。しかし、個々の三角形は底辺の長さがわからず、別々に面積を求めるのは難しそうです。
そこで、バラバラの三角形を「底辺と高さが変わらなければどんな形であっても同じ面積になる」という性質を用いて1つにまとめていきます。
それでは、この流れに沿って問題を攻略していきましょう!
下の三角形を上に持ってくる
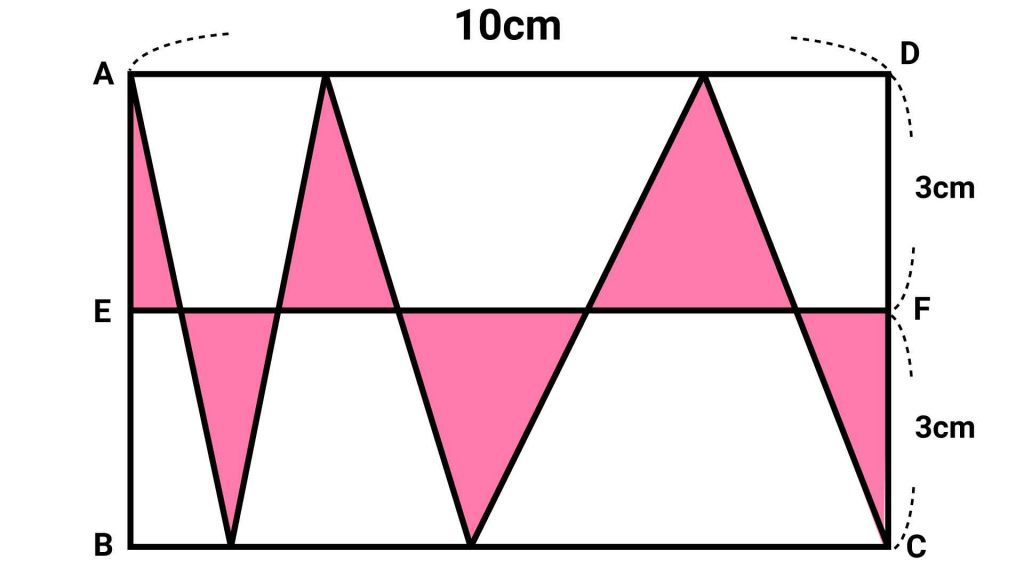
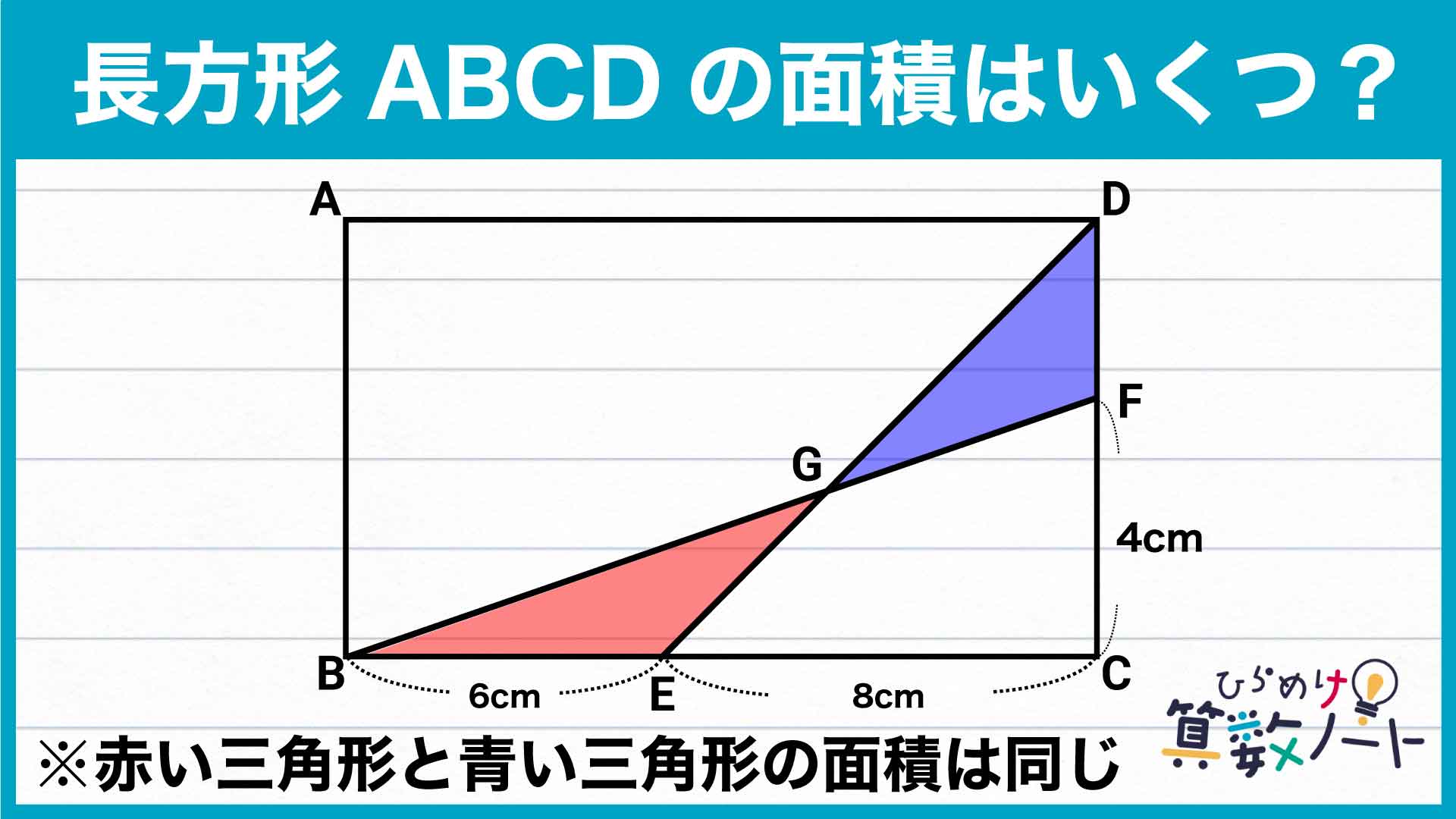
計算しやすくするため、問題図に以下のようにA~Fまでのアルファベットを振ります。
まずは四角形EBCFにある三角形を上に持ってきてみましょう。
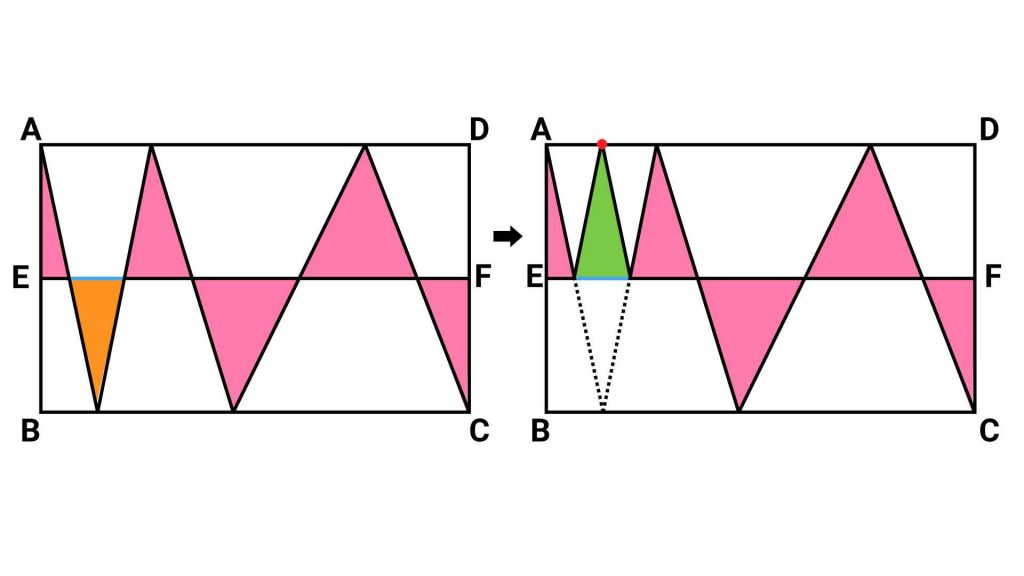
たとえば、下段一番左にあるオレンジ色の三角形に注目してみます。
左の図のオレンジ色の三角形は、底辺が青線で高さが3cmの三角形だと考えることができます。ここで、辺AD上に点を打って、右の図の緑色の三角形を作ってみましょう。すると、右の三角形も底辺が青線、高さが3cmですので左右の三角形は同じ面積であることがわかります。
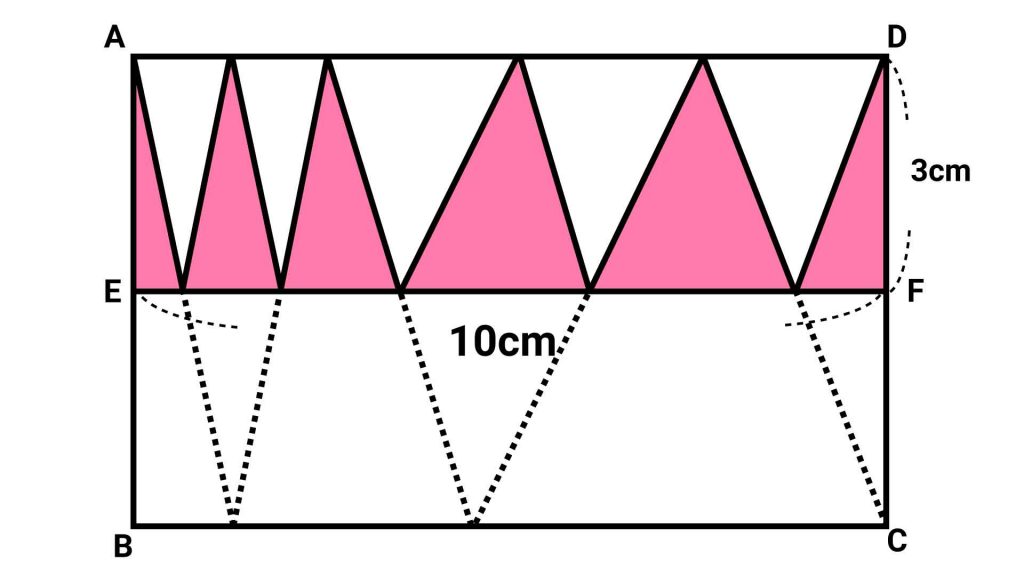
同様にほかの2つの三角形も移動してみましょう。すると、問題の図形の面積はこのように長方形の上側にまとめることができました。
6つの三角形を1つにまとめる
今度は上にまとめたバラバラの三角形を1つにまとめていきましょう。
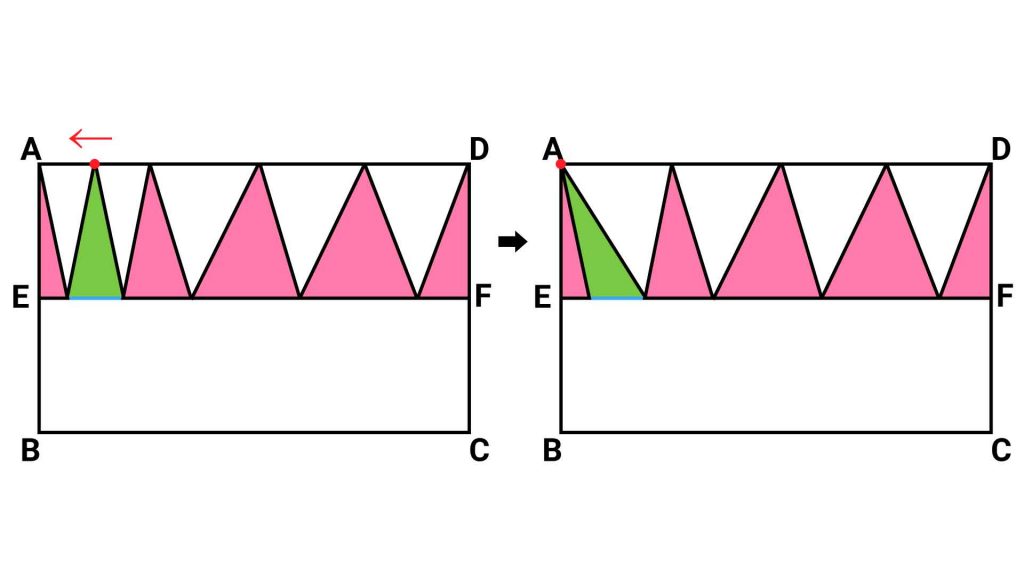
先ほどの緑色の三角形をもう一度例にあげてみましょう。辺ADと辺EFは平行なので、青線を底辺とすると頂点を辺ADのどこに動かしても高さが変わらないため、三角形の面積は変わりません。したがって、右の図のように移動させることができます。
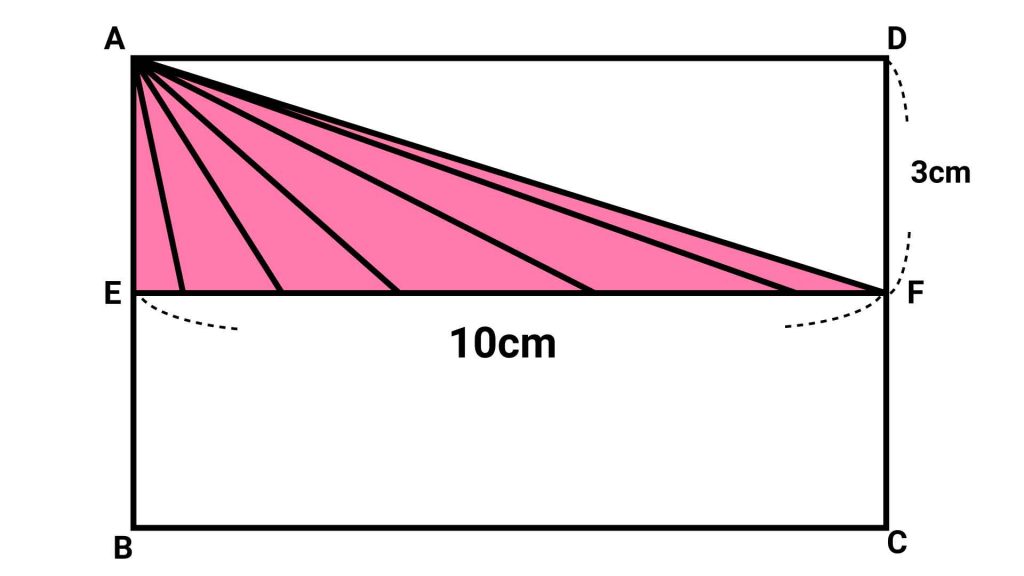
ほかの三角形も同様に変形すると、以下の図のように変形できます。
したがって色付けされた図形は上の図のように1つの大きな三角形にまとめることができ、この図の面積は10×3÷2=15cm2となります。
以上より、元の問題図の赤い図形の面積の合計も、15cm2となります。
答え:15cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)








.jpg)






