小学5年生レベルの「長さを求める問題」、あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

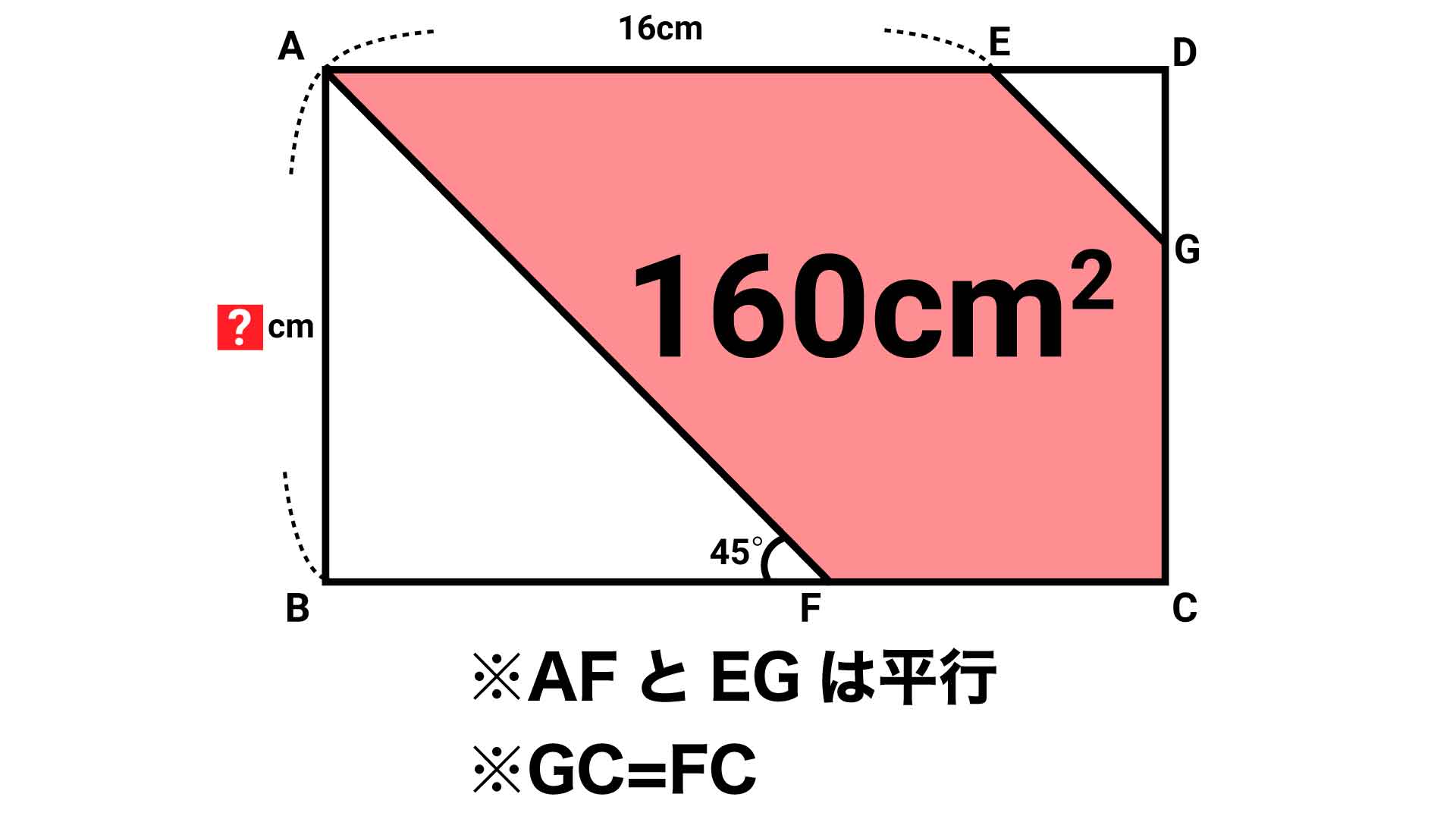
前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです。

今回の解き方をまとめた図がこちらです。

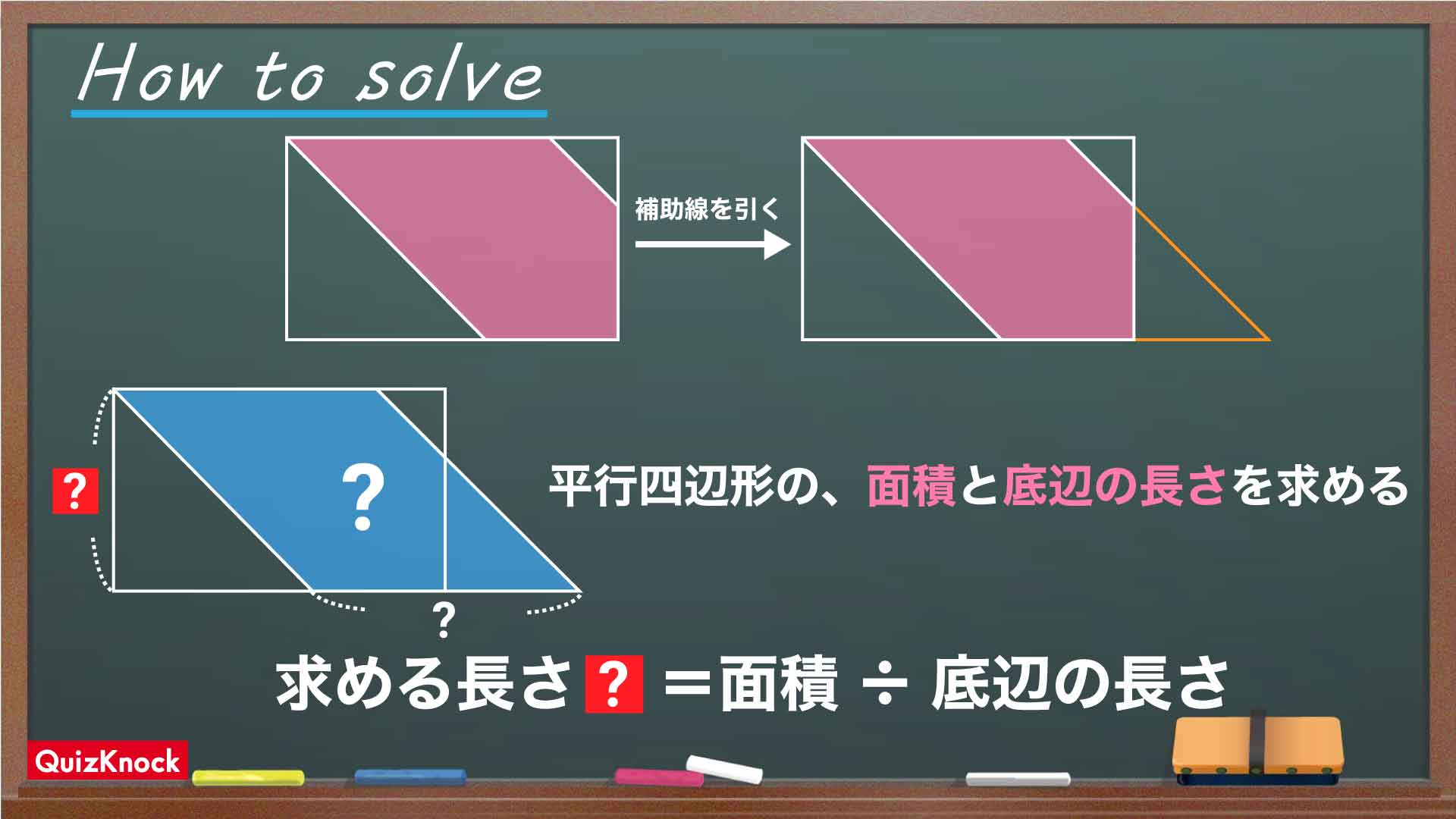
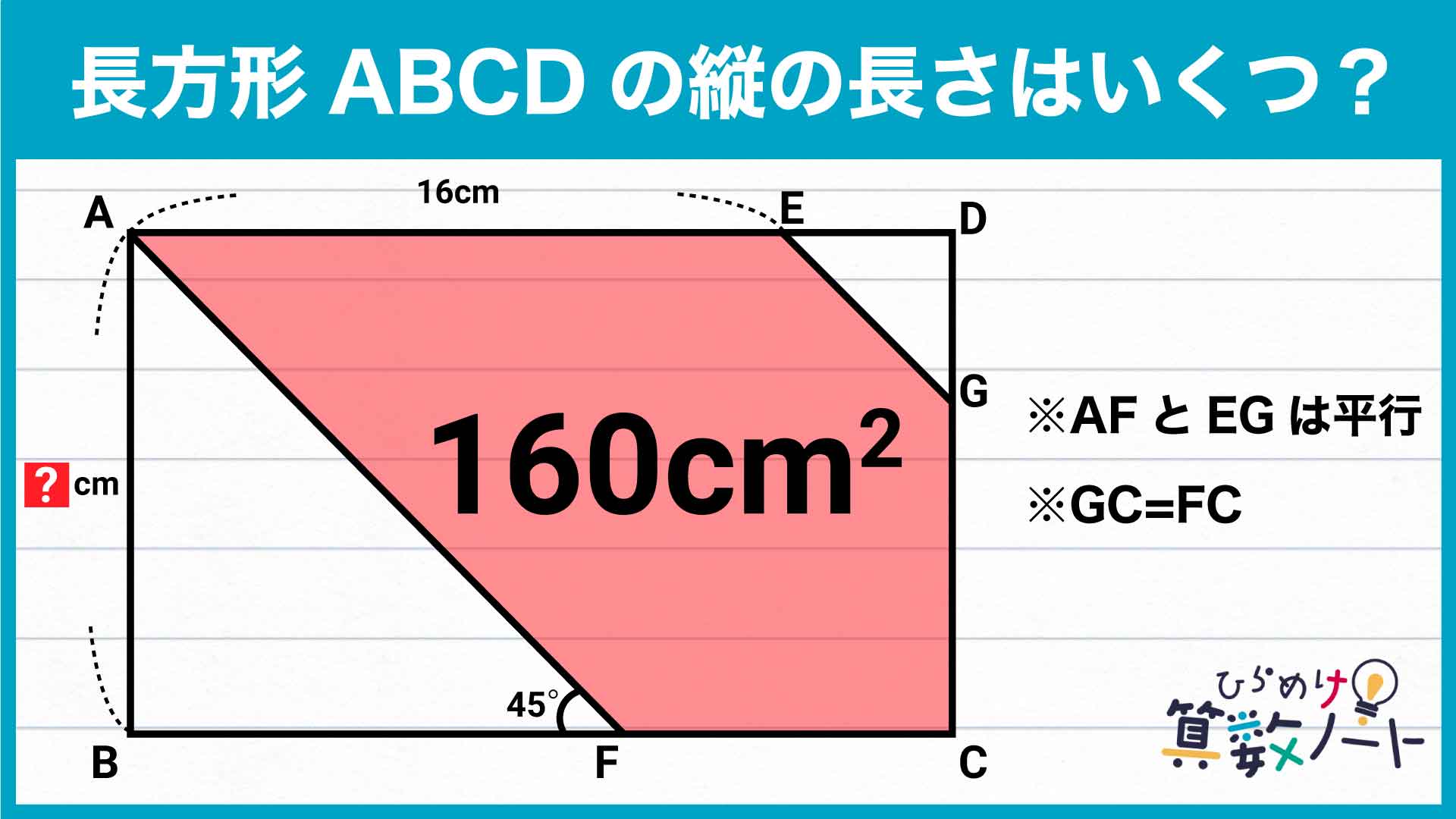
ポイントは、「面積を求める公式を逆算する」ことです。

赤い図形に補助線を引いて、平行四辺形を作ります。すると、長方形の縦の長さは平行四辺形の高さにあたることがわかります。

そのため、平行四辺形の面積と底辺の長さがわかれば、面積を求める公式を逆算して高さを求めることができます。

この流れに沿って、問題を攻略していきましょう！

補助線を引く

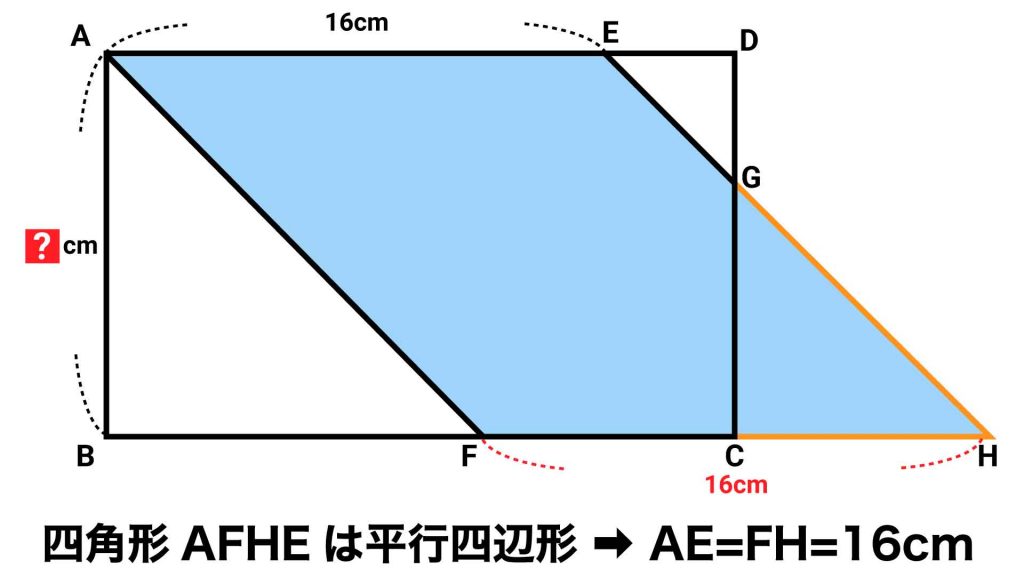
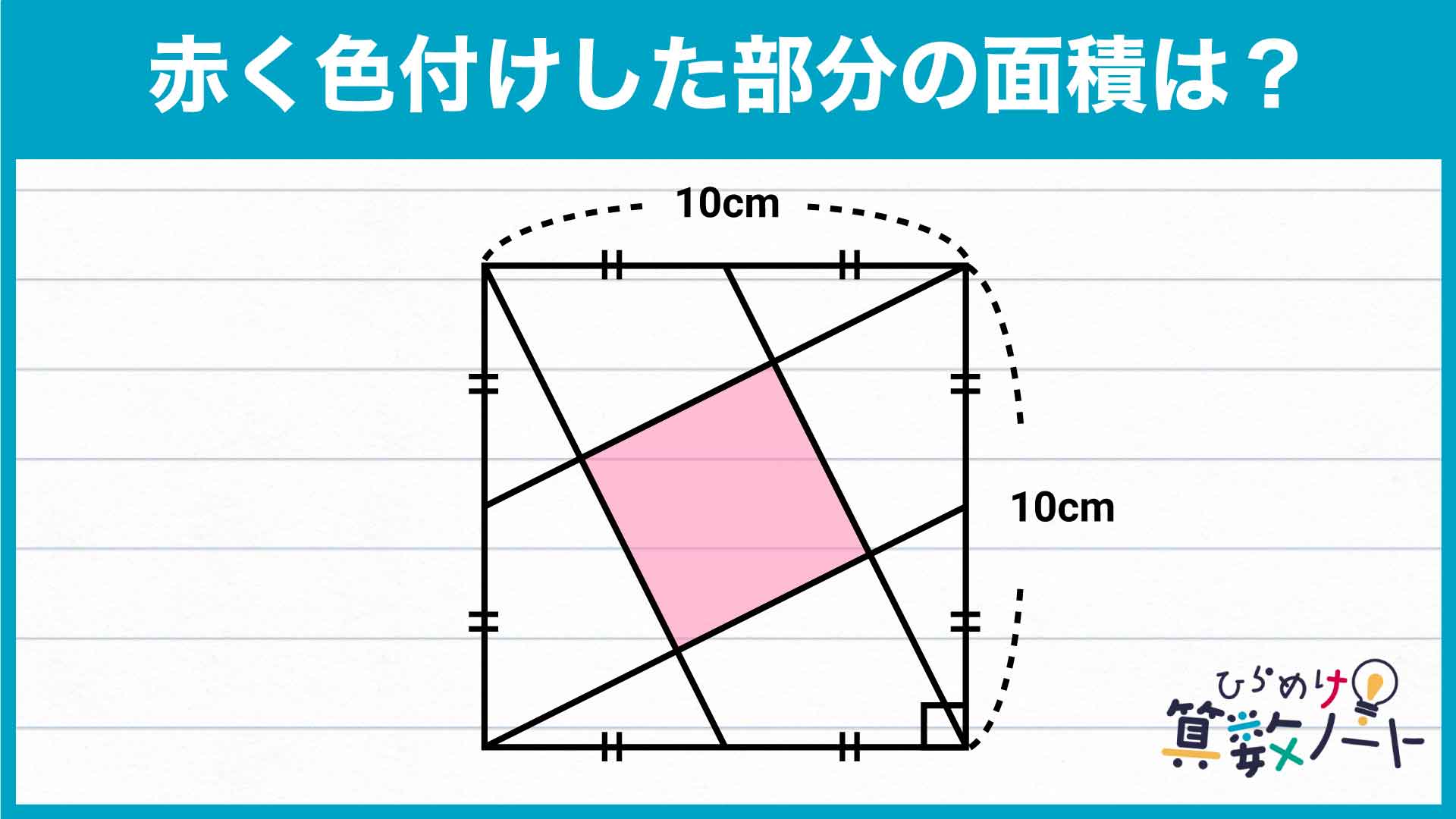
まずは、以下のようにEGとFCを延長します。延長して交わった点をHとします。

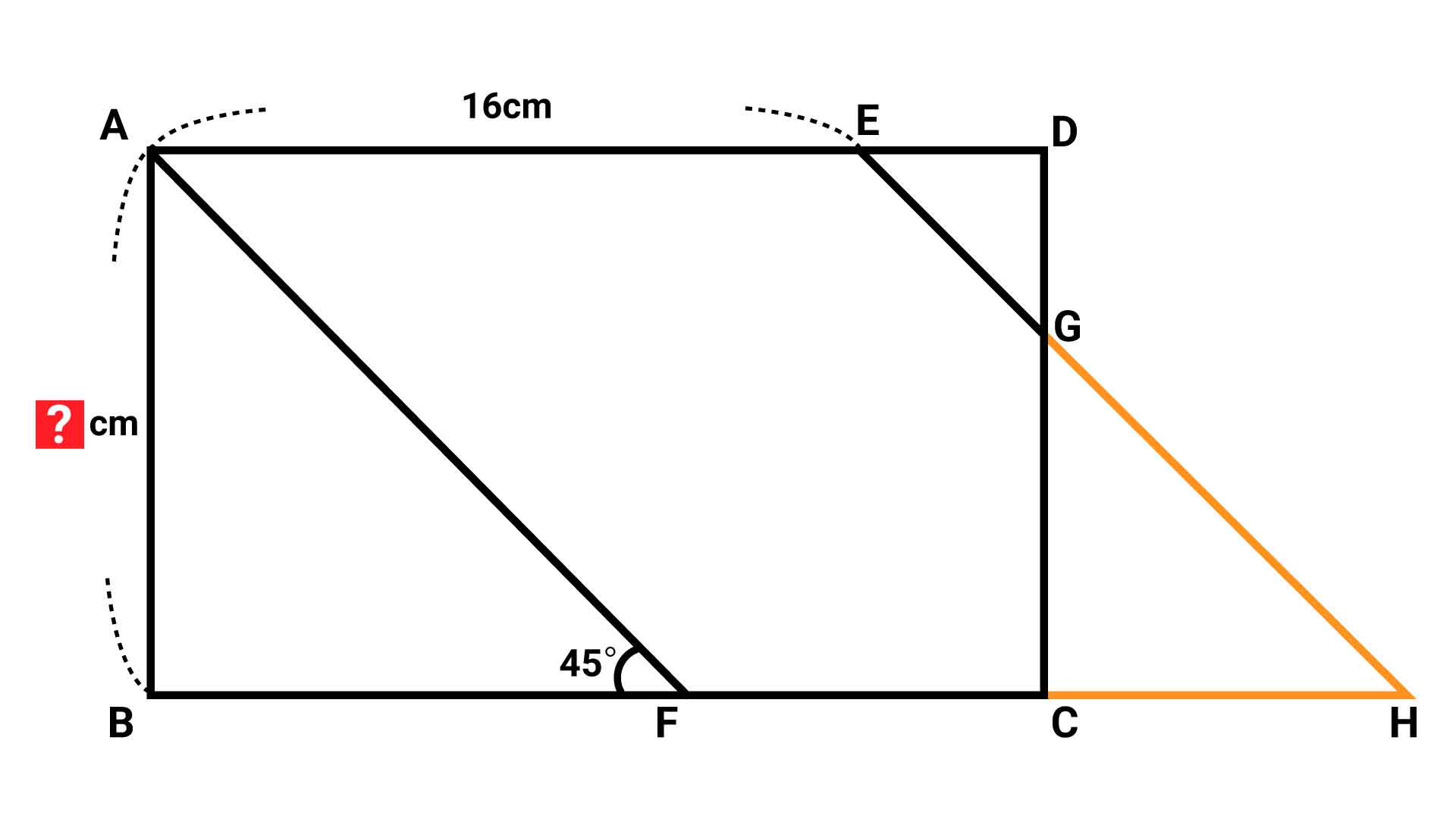
四角形AFHEの性質を調べる

四角形AFHEについて、AEとFH、AFとEHは、それぞれ互いに平行な関係にあります。すなわち、2組の対辺が平行なので、四角形AFHEは平行四辺形であることがわかります。

平行四辺形は対辺の長さが等しいので、AE=FH=16cmとなります。つまり、平行四辺形の底辺の長さは16cmです。

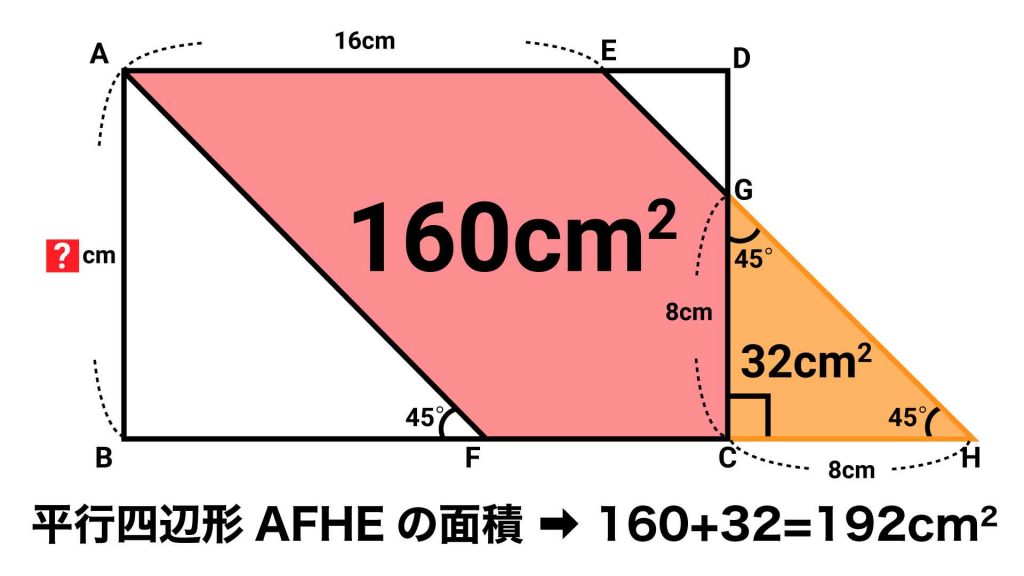
平行四辺形AFHEの面積は、もともとの赤い図形の面積と、三角形GCHの面積を足し合わせて求められます。条件より、赤い図形の面積は160cm²とわかっているため、ここからは三角形のGCHの面積を求めていきます。

三角形GCHの性質を調べる

条件より、AFとEGは平行なので、AFとEHも平行です。平行線の同位角は大きさが等しいので、角GHC=角AFB=45度です。

また、四角形ABCDは長方形であることより角GCH=90度であるので、角HGC=45度となります。

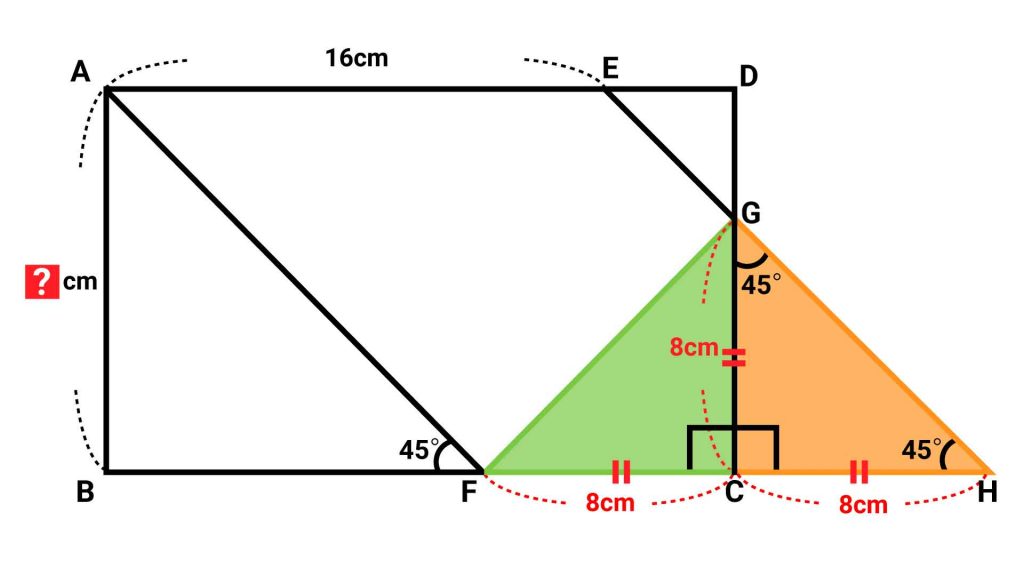
したがって、三角形GCHの2つの角が45度であることから、三角形GCHは直角二等辺三角形だとわかります。

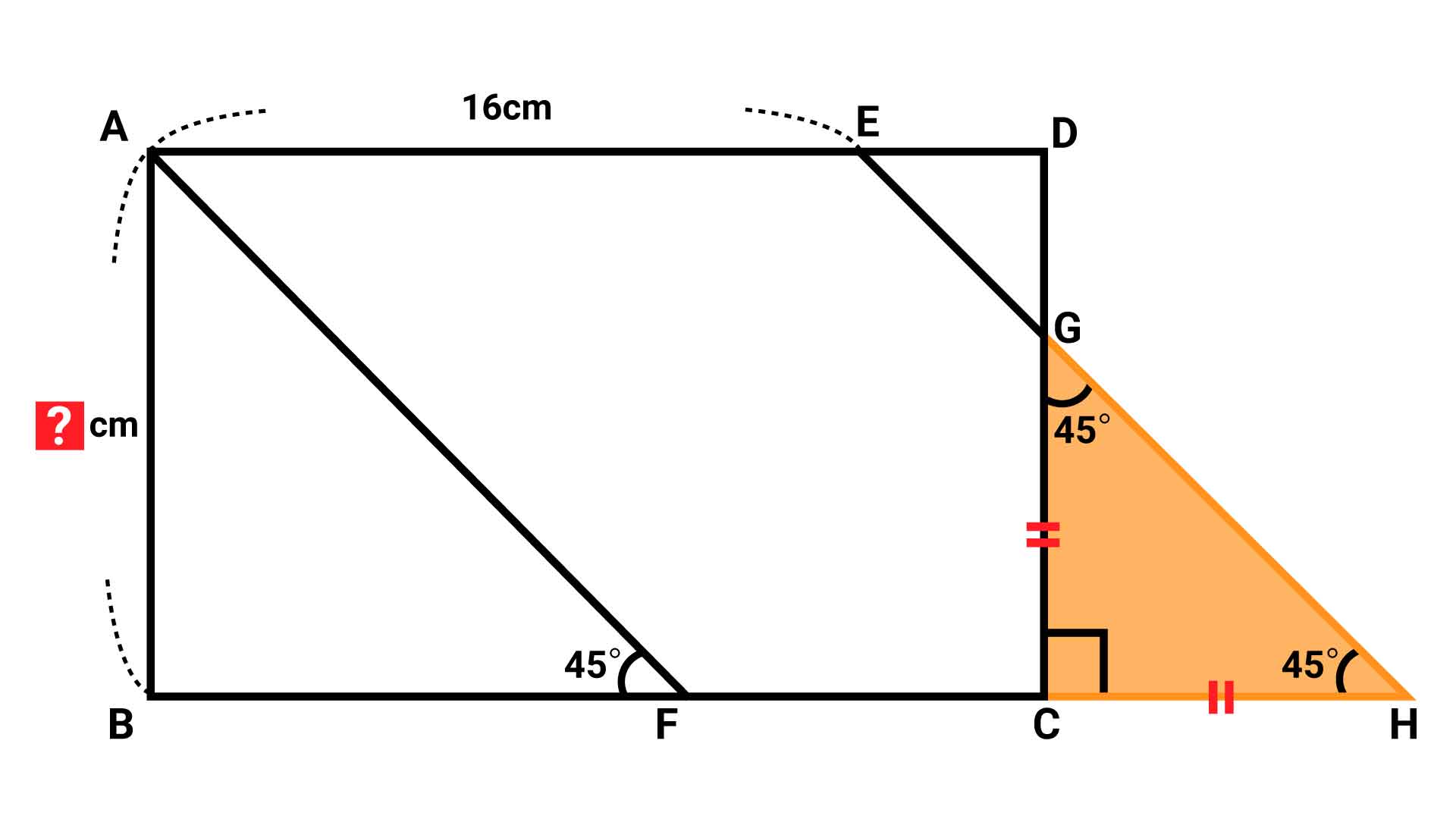
また、条件よりGC=FCであるため、三角形CGHが直角二等辺三角形であることを踏まえると、GC=FC=CHであることがわかります。

FHは平行四辺形AFHEの底辺であるため16cmです。CはFHを二等分する点なので、FC=CH=8cmとなります。

さらに、GC=FC=CHであることから、GCも8cmとなります。

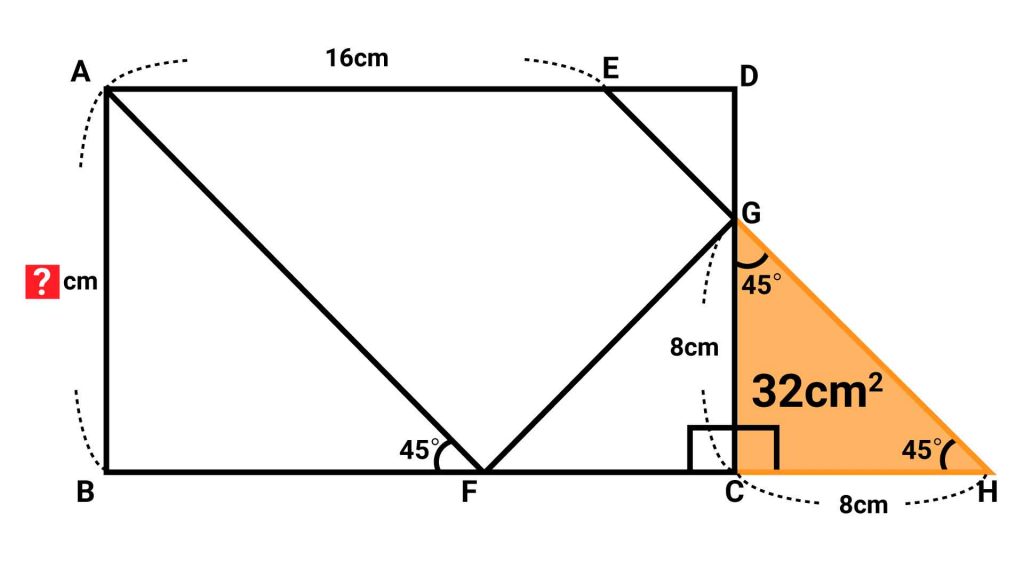
三角形GCHの面積を求める

三角形GCHは、底辺、高さがともに8cmの直角二等辺三角形です。したがって面積は、8×8÷2=32cm²となります。

平行四辺形AFHEの面積を求める

平行四辺形AFHEの面積は、赤い図形の面積と、三角形GCHの面積を足し合わせたものです。

赤い図形の面積は、条件より160cm²です。また、三角形GCHの面積は、32cm²です。

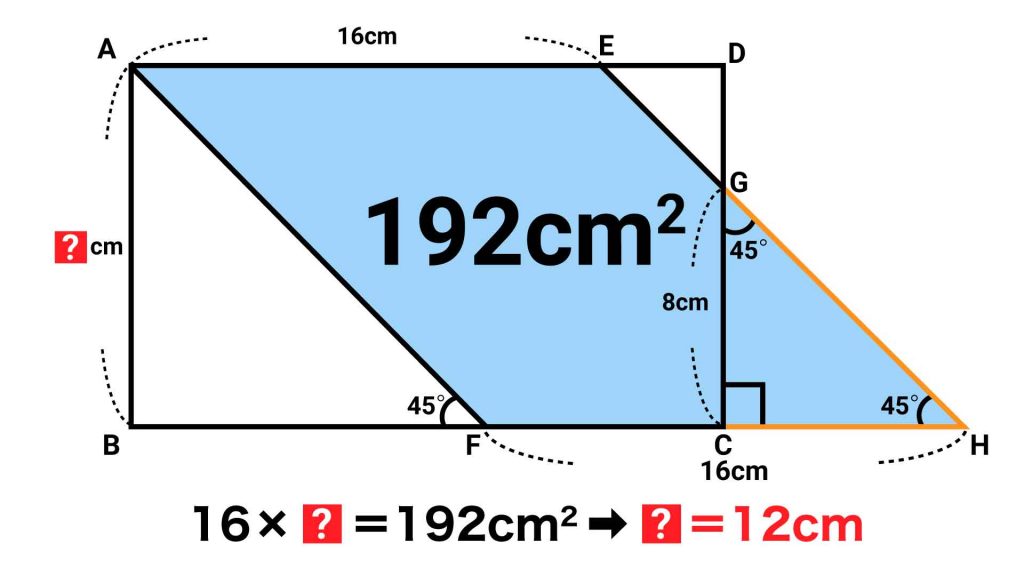
したがって、平行四辺形AFHEの面積は、160+32=192cm²とわかります。

長方形の縦の長さ=平行四辺形AFHEの高さ

求めたい長方形の縦の長さは、平行四辺形AFHEの高さと同じでした。この高さは、平行四辺形AFHEの面積÷底辺の長さで求めることができます。

したがって、長方形の縦の長さは192÷16=12cmとなります。

答え：12cm

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】