解説
それでは解説です。さまざまな解き方がありますが、ここでは「小学6年生で解ける」解き方を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
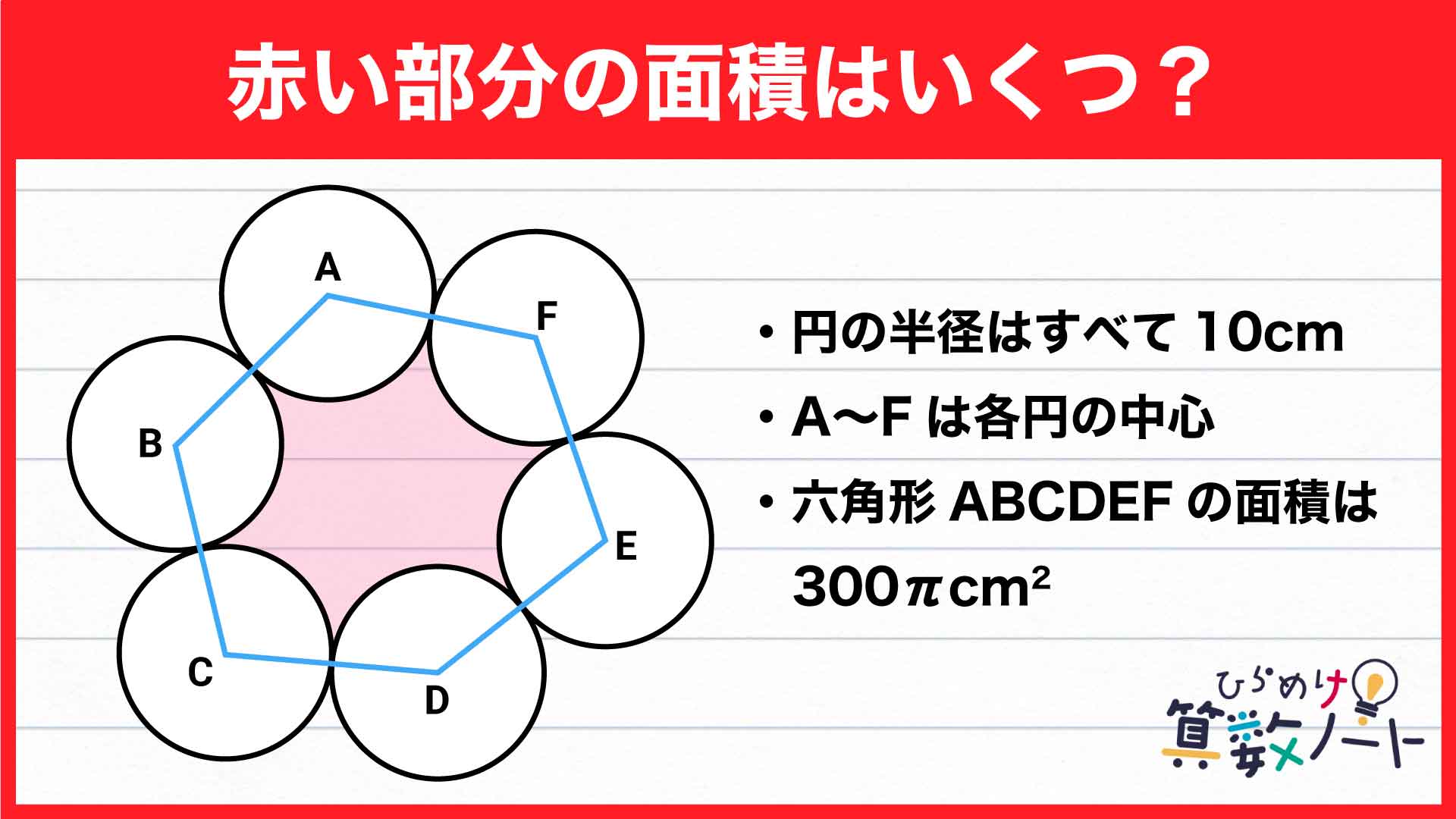
それでは私と一緒に解いていきましょう! 面積を求める図形がいびつな形をしていますが、一体どこから手をつければよいのでしょうか。
ひとまず、赤色の部分の面積を求めるために、何の情報が必要かを整理します。
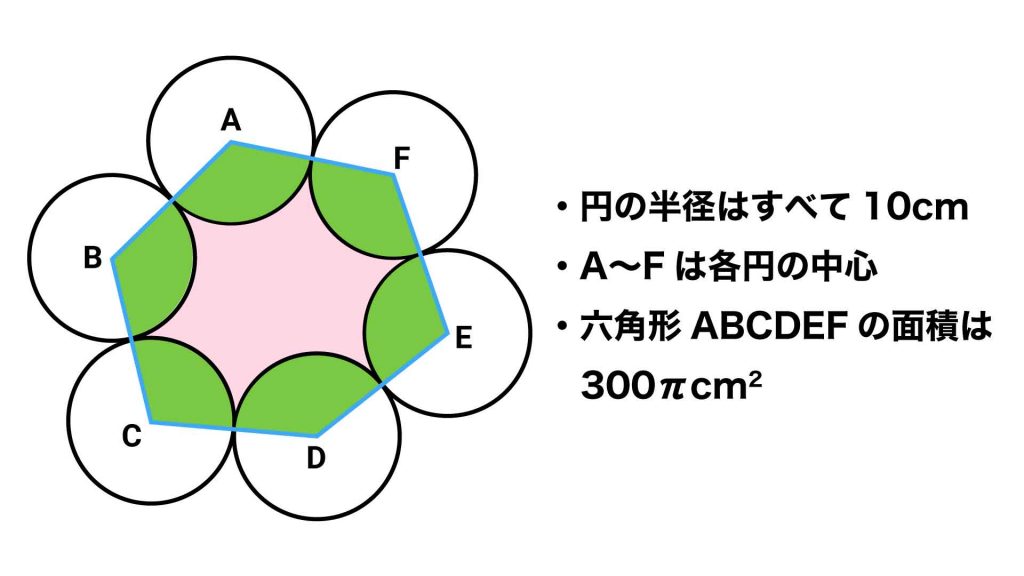
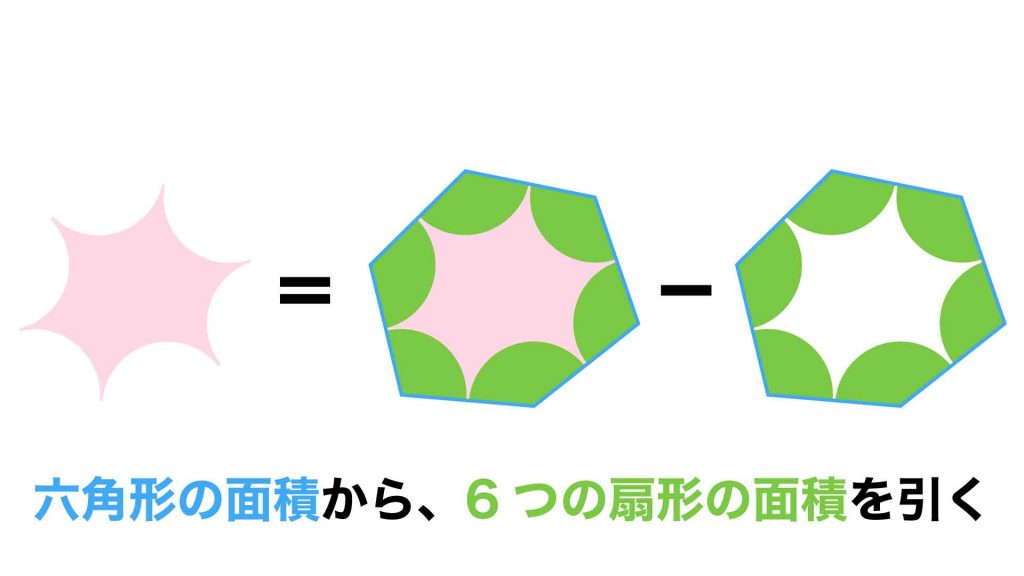
赤色の部分の面積は、青い六角形の面積から、下の図の緑色の扇形の面積の合計を引くことで求められます。
青色の六角形の面積はすでに情報として与えられているので、緑色の扇形の面積の合計を求めることができれば、答えを求めることができます。
ここがポイント!
扇形の半径が10cmとわかっているので、中心角がわかれば、面積を求めることができます。しかし今回の問題においては、ひとつひとつの扇形の中心角を求めるのは難しそうです。
そこで、発想の転換が重要になります。個々の扇形の中心角を求められないのであれば、扇形の中心角の合計が何度であるかを求め、それが「同じ半径を持つ円何個分に相当するか」を考えます。
例えば、扇形の中心角の合計が540度である場合、540度÷360度(円一周)=1.5となり、円1.5個分の面積を持つことがわかります。
これを踏まえて、問題を解いていきましょう!
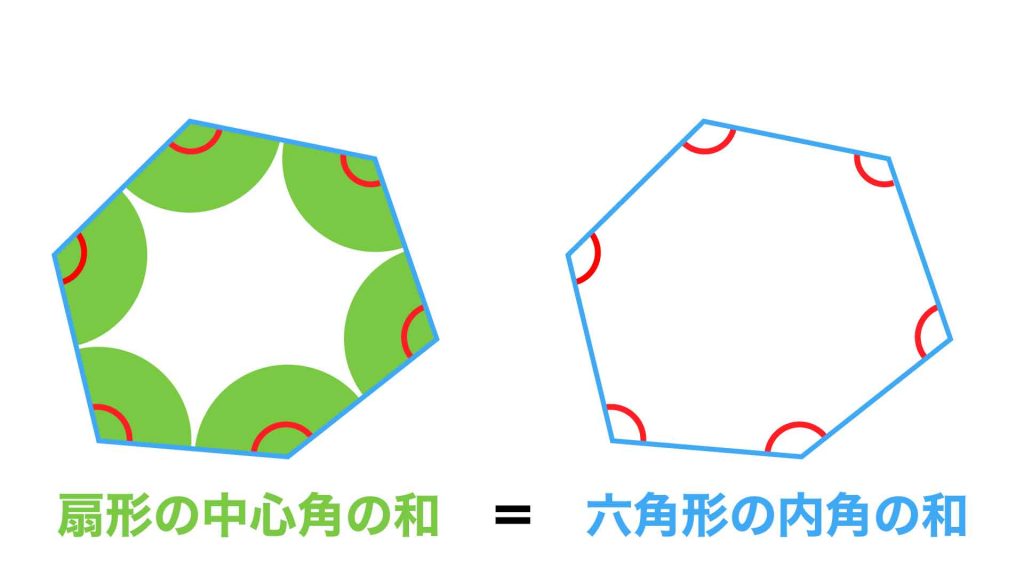
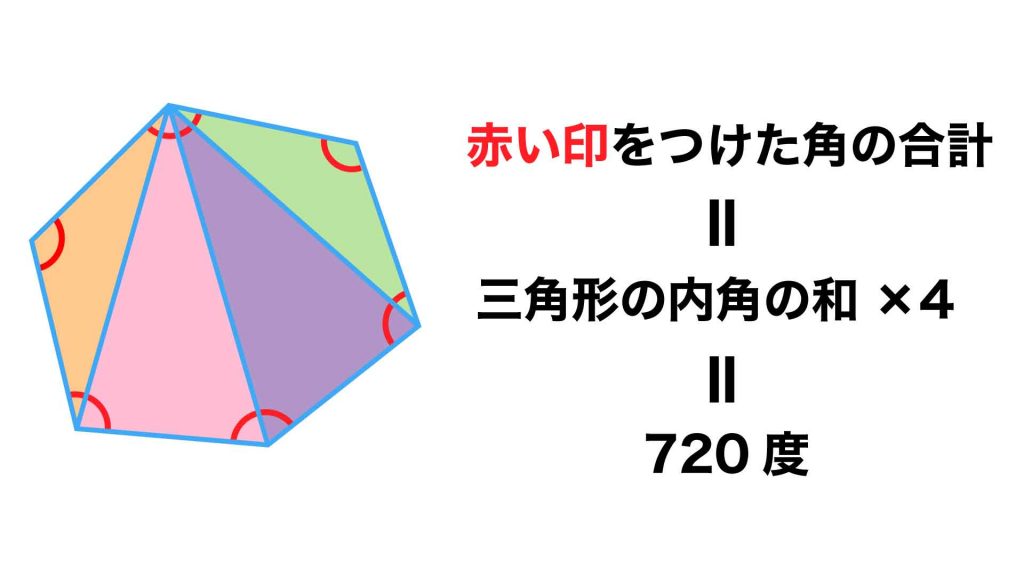
6つの扇形の中心角の和=六角形の内角の和
緑色の扇形は、各円の中心を線で結んだ六角形と、円の共通部分です。
したがって、緑色の扇形の中心角の和は、六角形の内角の和に一致していることがわかります。
六角形の中には4つの三角形があり、三角形の内角の和は180度なので、六角形の内角の和は180度×4=720度とわかります。
したがって、緑色の扇形の中心角の和は720度となります。
これでやっと扇形の面積の合計が求められますね!
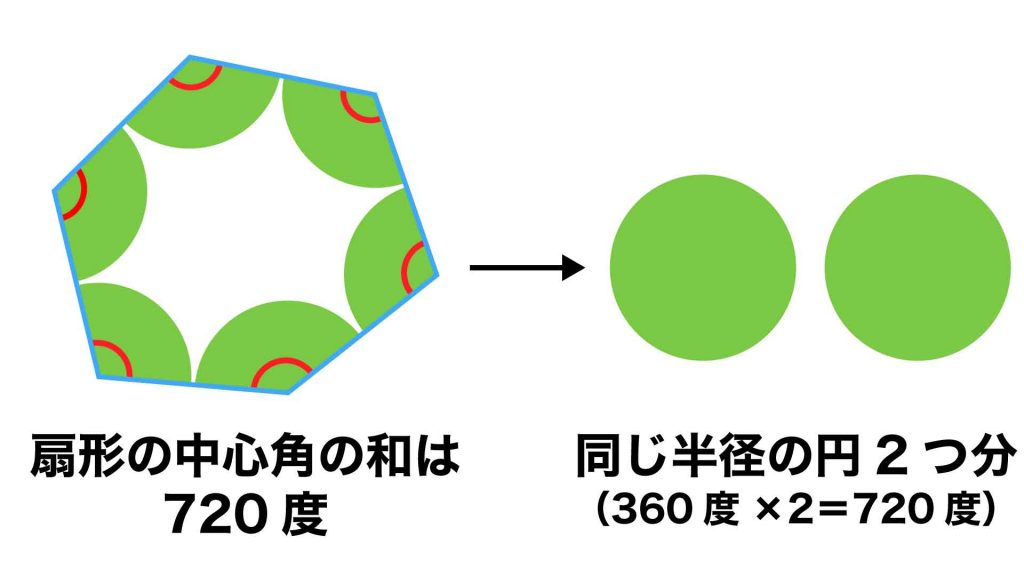
扇形の合計の面積を求める
円の一周の角度は360度なので、360度×2=720度であることより、緑色の扇形の面積の合計は円の面積2つ分であることがわかります。
円の半径は10cmなので、円1つの面積は10×10×π=100πcm2となります。
したがって、円2つの面積、すなわち6つの扇形の面積の合計は100π×2=200πcm2です。
赤色の部分の面積は、青い六角形の面積から緑色の扇形の面積の合計を引いたものでした。
したがって面積は、300π-200π=100πcm2となります。
答え:100πcm2
扇形の中心角の和が六角形の内角の和と同じであることに気がつき、扇形の合計の面積を求められるかがポイントでした。
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)









.jpg)







