解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回も僕と一緒に解いていきましょう! 長方形の面積を求めるには、どの部分の長さがわかればいいでしょうか?
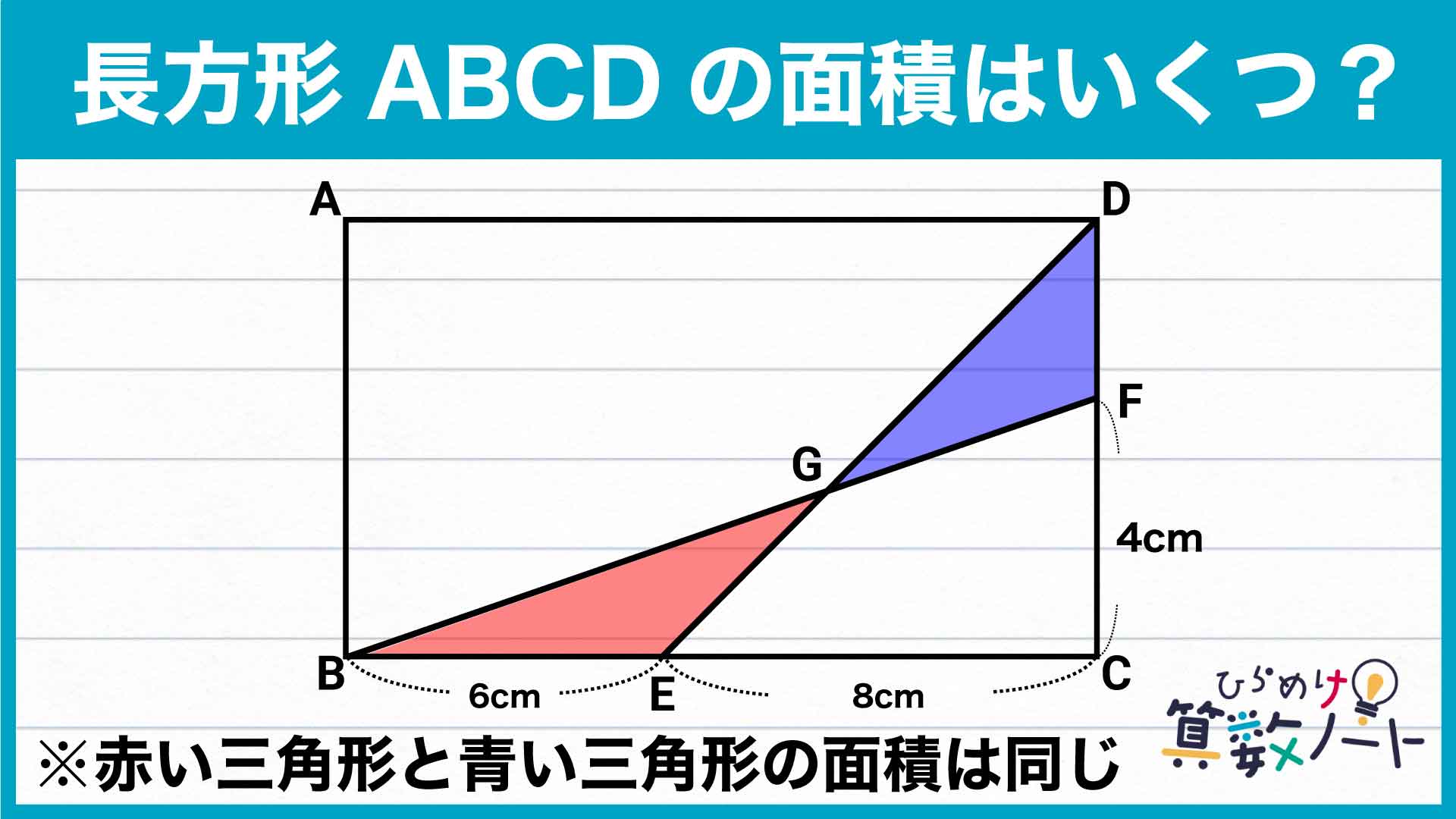
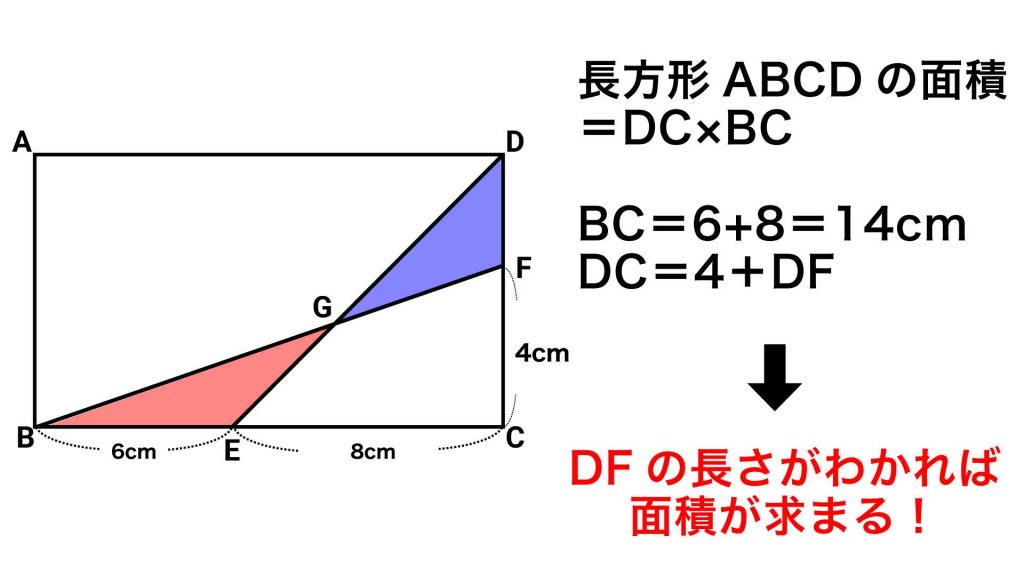
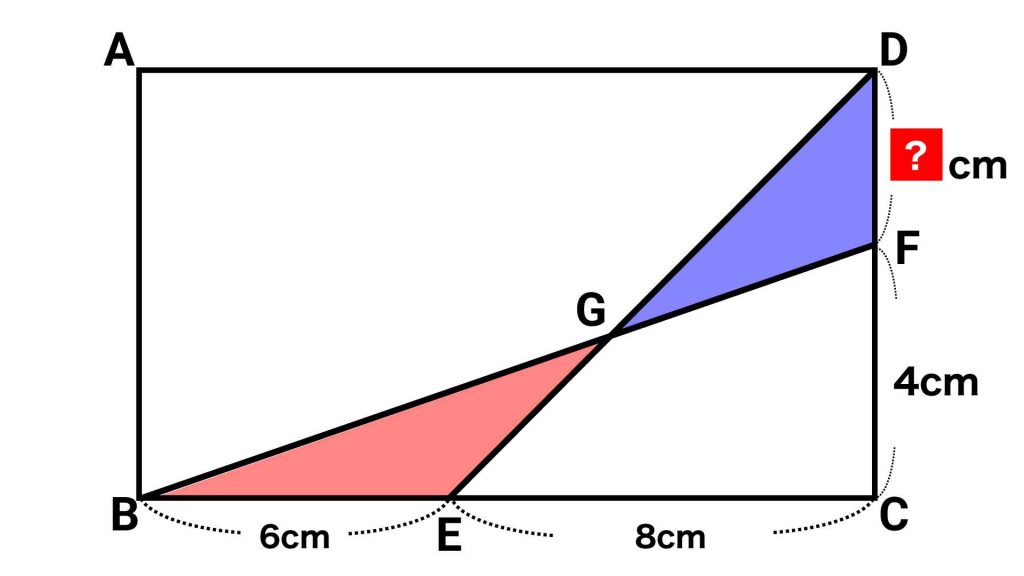
今回の問題で求めるのは、大きな長方形ABCDの面積です。
長方形の面積は、(縦の長さ)×(横の長さ)で求められます。
問題から、長方形の横の長さ(BE+EC=14cm)と、縦の長さの一部(FC=4cm)は明らかになっています。
したがって、DFの長さがわかれば、長方形の縦の長さがわかるため、長方形ABCDの面積を求めることができます。
DFの長さを求めるのに必要なのが、「赤と青の三角形の面積が同じ」という情報です。
この情報からどのようにDFの長さ求めるのか、これから解説していきます!
「赤と青の三角形の面積が同じ」ということは……?
「赤と青の三角形の面積が同じ」という情報から、「どちらかの面積を求める」という方針を立ててしまいがちですが、この問題では赤と青の三角形の面積を求める必要はありません!
ここで大事なのは、「面積が同じという条件を利用して、DFの長さを出す」ということです。
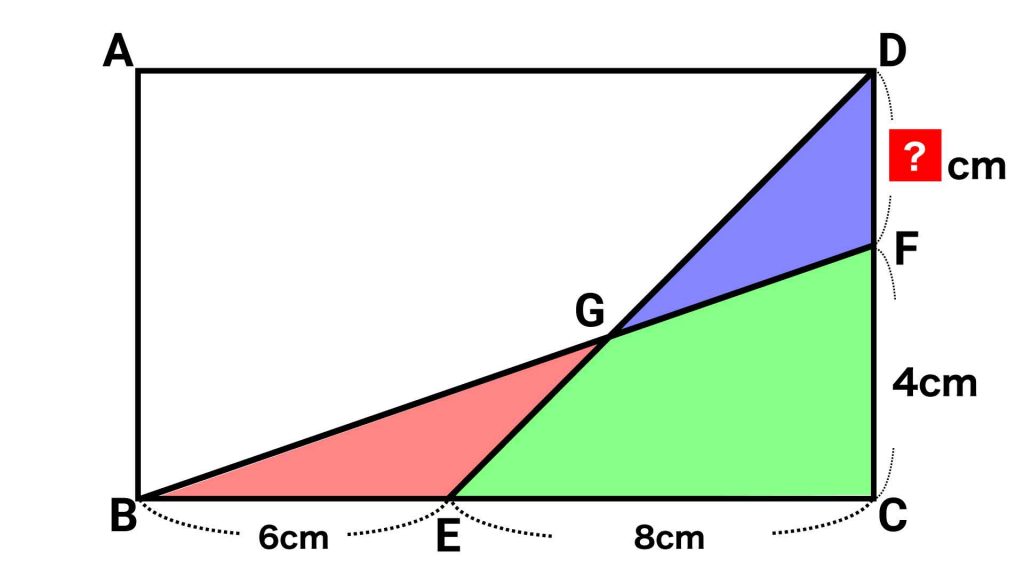
では、この条件をどのように利用すればいいのでしょうか? ここで着目すべきは、四角形GECFです。
この四角形に着目すると、同じ面積を持つ三角形のペアがもう1組見えてきます。
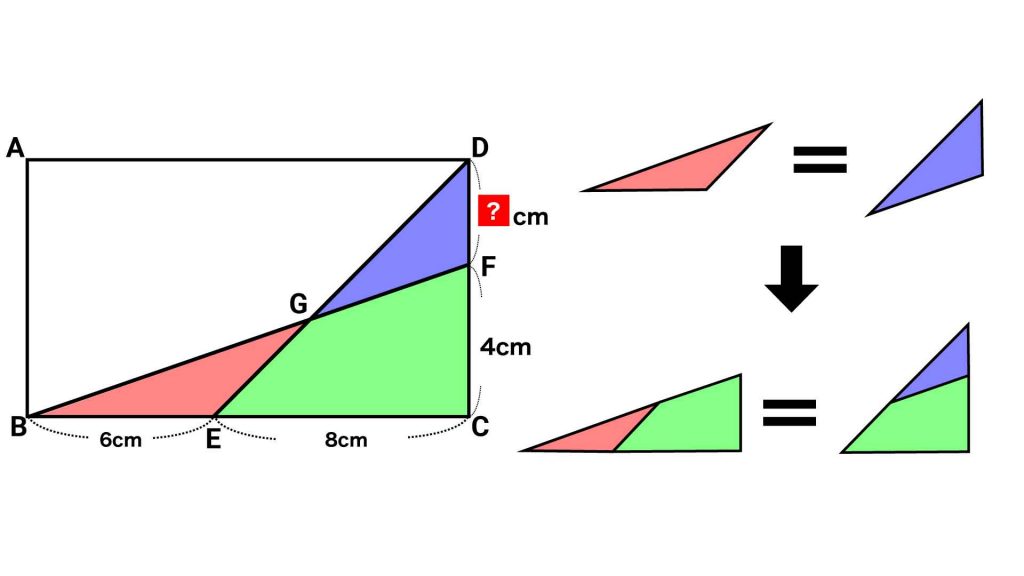
赤い三角形と緑の四角形を組み合わせると、ひとつの三角形FBCになります。
同様に、青い三角形と緑の四角形を組み合わせると、ひとつの三角形DECになります。
赤い三角形と青い三角形は同じ面積であり、かつ緑の四角形は共通部分なので、三角形FBCと三角形DECの面積は同じになります。
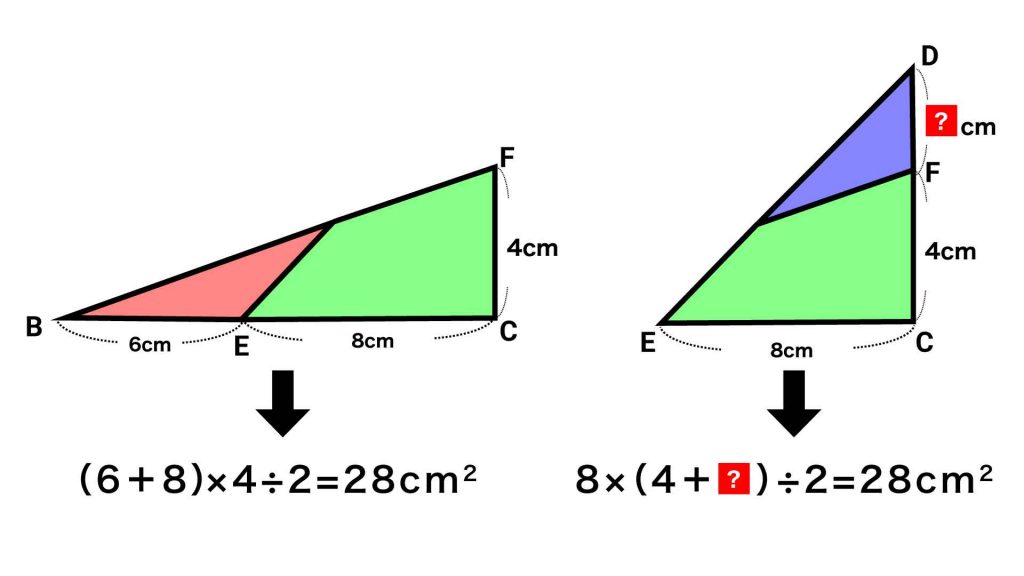
三角形FBCの面積は、(6+8)×4÷2=28cm2です。したがって三角形DECの面積も28cm2です。
三角形DECの面積は8×(4+DF)÷2で表され、これが28cm2となります。
上の式中にある「?」の部分(DFの長さ)は、以下のように式を変形すると求めることができます。
数字をかけたり、割ったり、引いたりして、「=」の左側が「?」だけになるように式を変形します。
以上より、DFの長さは3cmと求められます。
長方形ABCDの縦の長さは4+3=7cmとなるので、長方形ABCDの面積は、14×7=98cm2となります。
答え:98cm2
面積が同じ三角形を、うまく活用できるかどうかがカギでした。
それでは。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)









.jpg)