解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
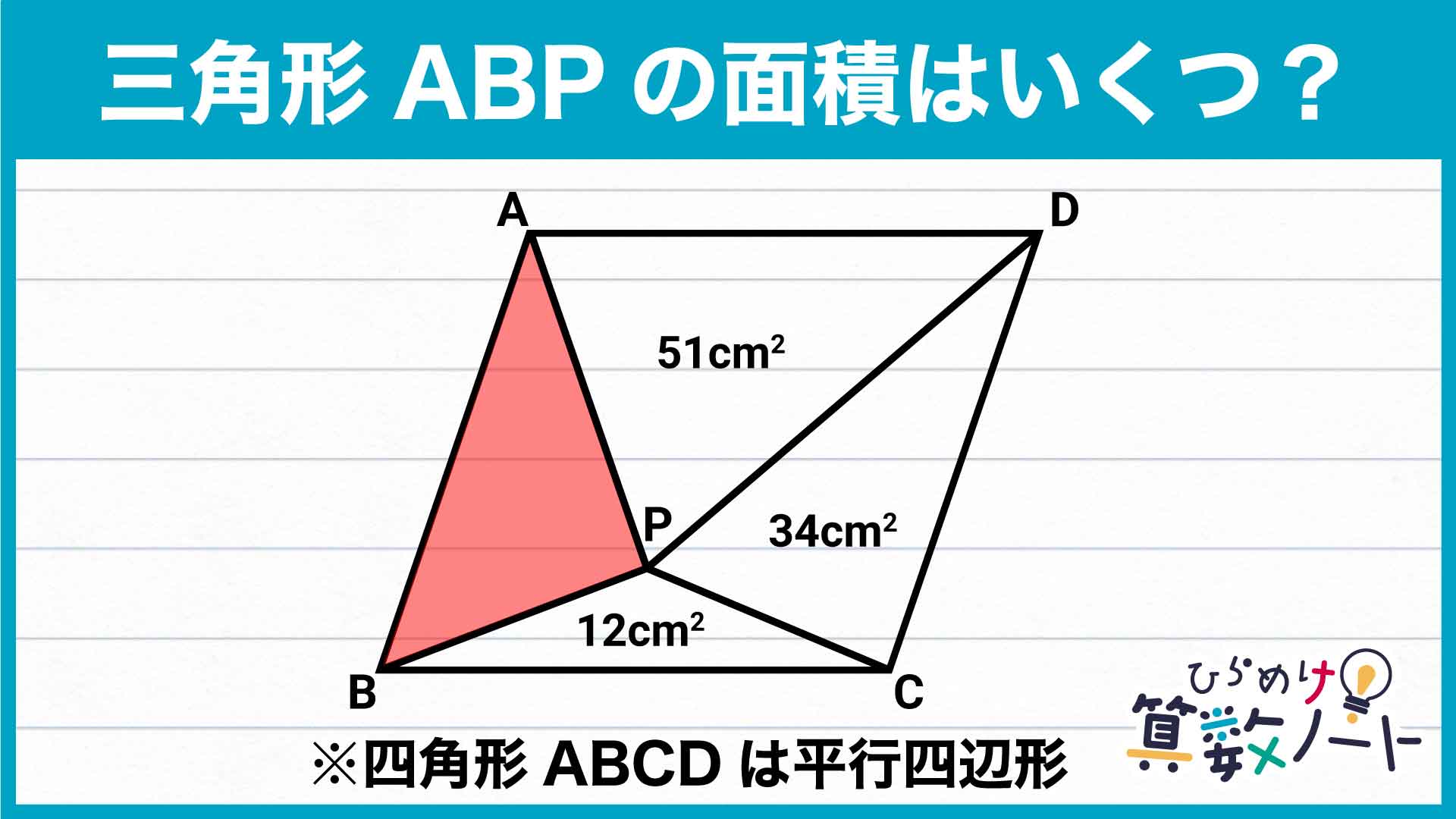
今回も僕と一緒に解いていきましょう! 与えられた情報は面積だけ! 手強そうです……。
今回の問題を解くにあたり、底辺や高さの具体的な値を求める必要は一切ありません!
代わりに必要となる情報は、「平行四辺形の面積」です。
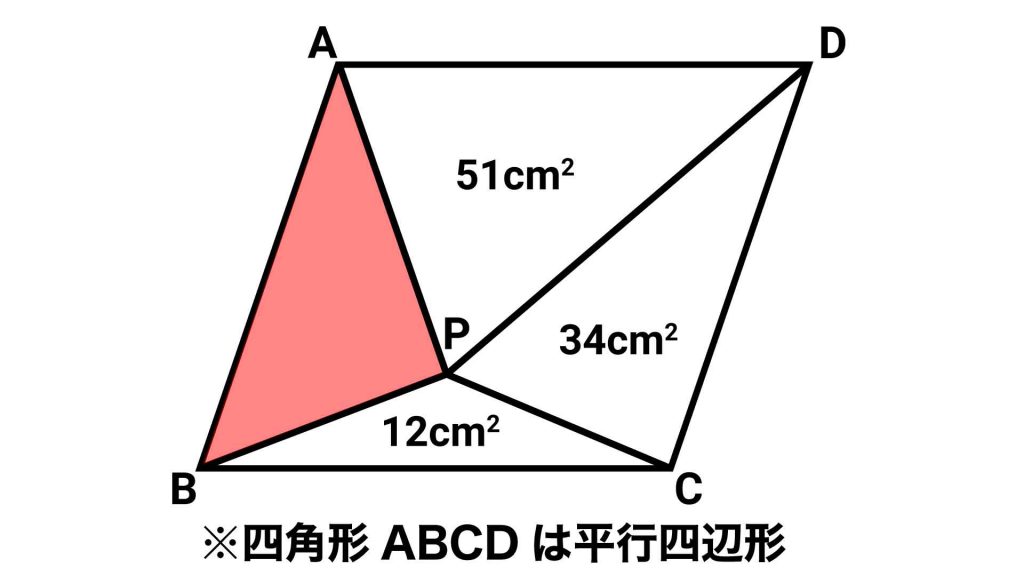
平行四辺形の面積がわかれば、3つの三角形の面積を引くことで、赤い三角形の面積を求めることができます。
それでは、解説していきます!
ステップ1:平行四辺形の面積を求める
平行四辺形の面積を求めるには、ふつう底辺と高さをかけ合わせます。ところが今回はそれがわかっていないため、他のもので表すことができないか考える必要があります。
これを考えるために、補助線として平行四辺形の高さにあたる線を引きます。具体的には、Pを通り、辺BC、ADに垂直な直線です。
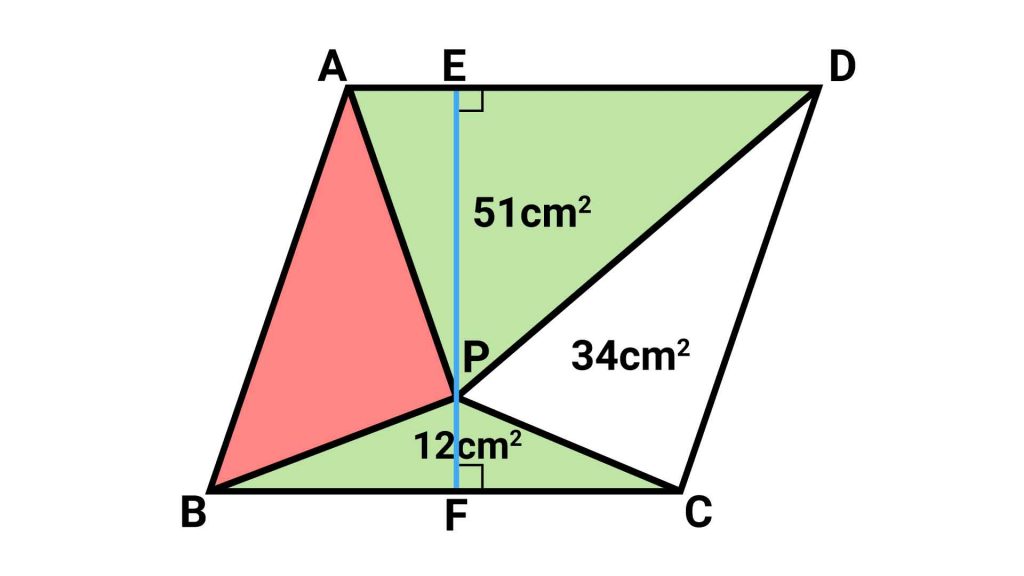 ▲底辺BCと線分EFをかけた値が、求めたい平行四辺形の面積だとわかる
▲底辺BCと線分EFをかけた値が、求めたい平行四辺形の面積だとわかる
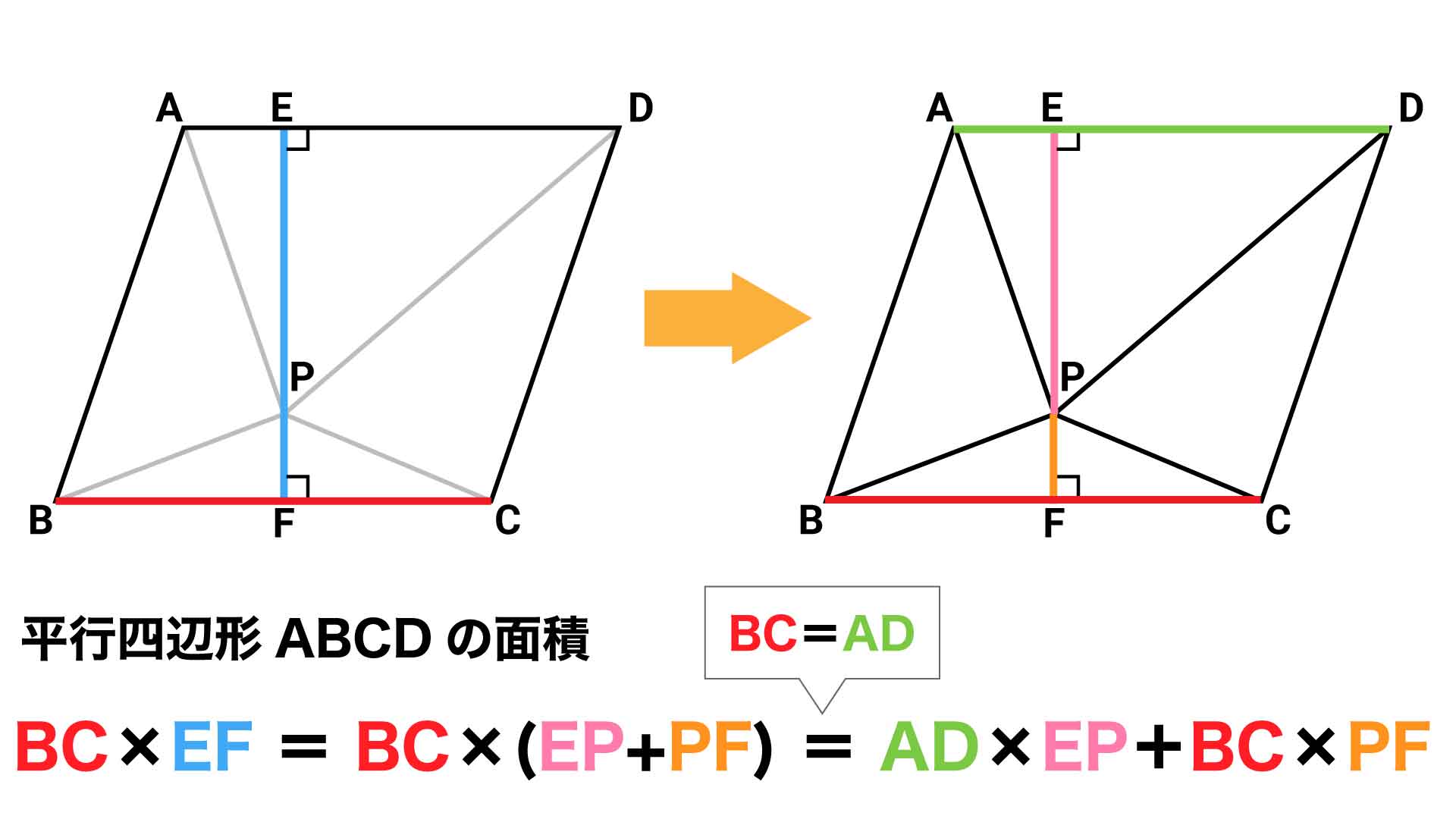
ここでポイントなのが、この線分EFの長さは、上図における2つの緑の三角形の高さ(線分EPとPF)を足したものであるということです。
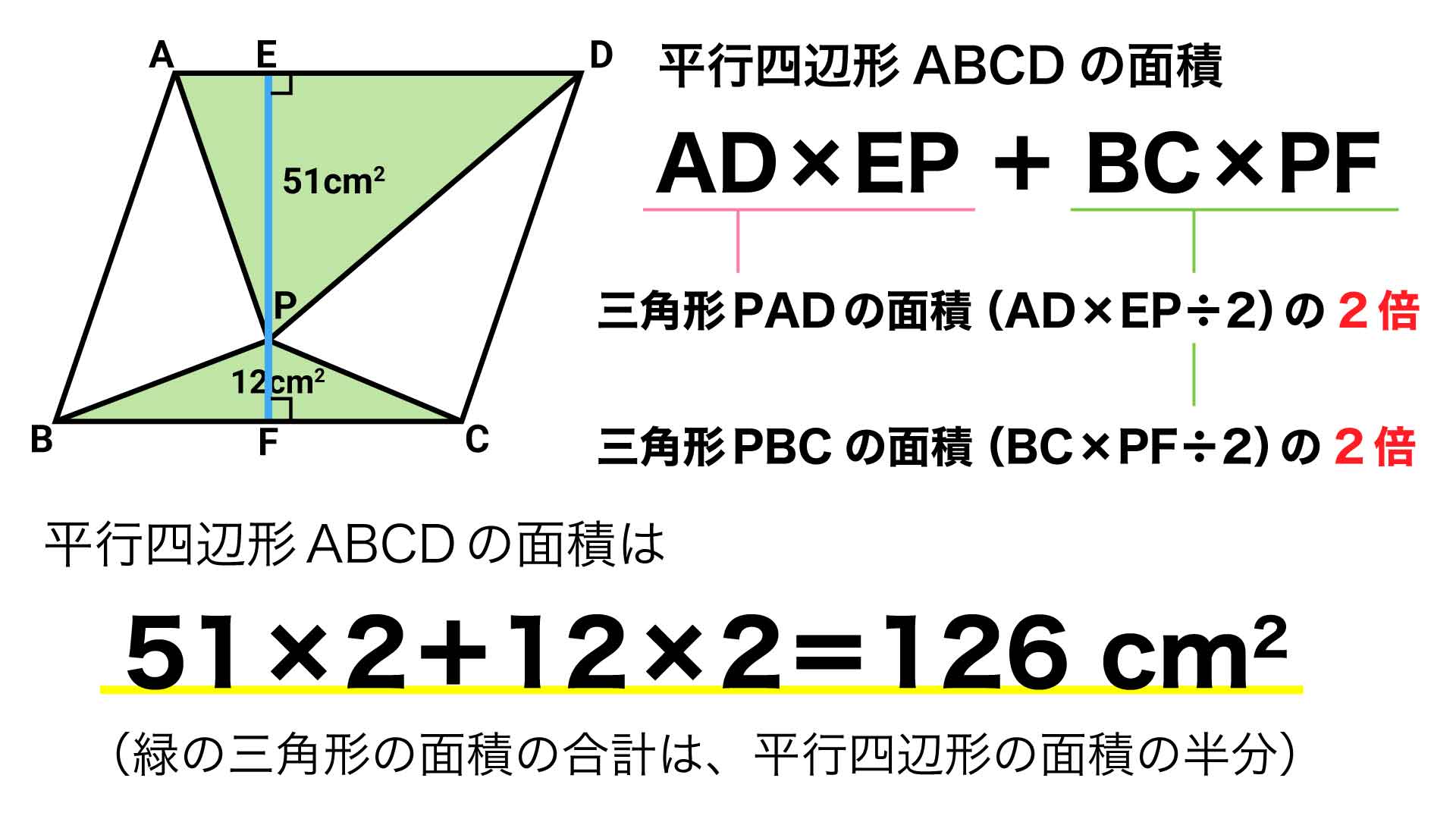
つまり、求めたい平行四辺形の面積は、BC×EF=BC×(EP+PF)と表すことができます。またBC=ADなので、上の式は2つの緑の三角形の底辺と高さを使ってAD×EP+BC×PFと書くこともできます。
三角形の面積は「底辺×高さ÷2」で求められるため、平行四辺形の面積は、緑の三角形の面積をそれぞれ2倍して足したものだといえます。
緑の三角形の面積はもう与えられていましたよね。
上記から、平行四辺形の面積は126cm2であることがわかりました。
ステップ2:赤い三角形の面積を求める
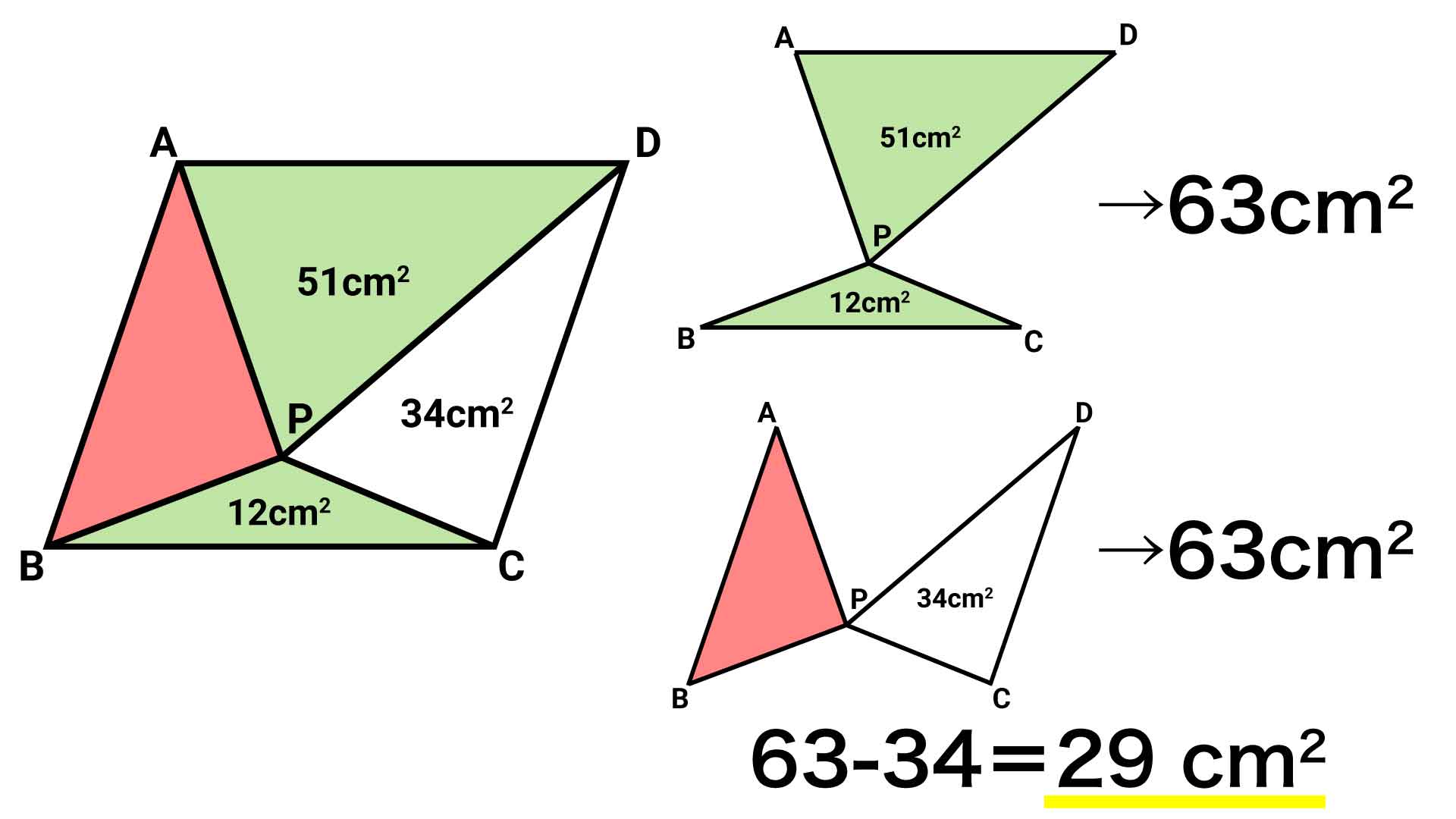
平行四辺形の面積がわかったため、ここから面積が明らかになっている3つの三角形の面積を引けば、赤い三角形の面積になります。
よって、赤い三角形の面積は126-(51+12+34)=29cm2です。
答え:29cm2
緑の三角形の面積の合計が、平行四辺形の面積の半分ということから、以下のようにも求めることができます。
平行四辺形の面積を三角形の底辺や高さで表すことができるかがポイントでした。
それでは。
【あわせて読みたい】










.jpg)










.jpg)







