解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
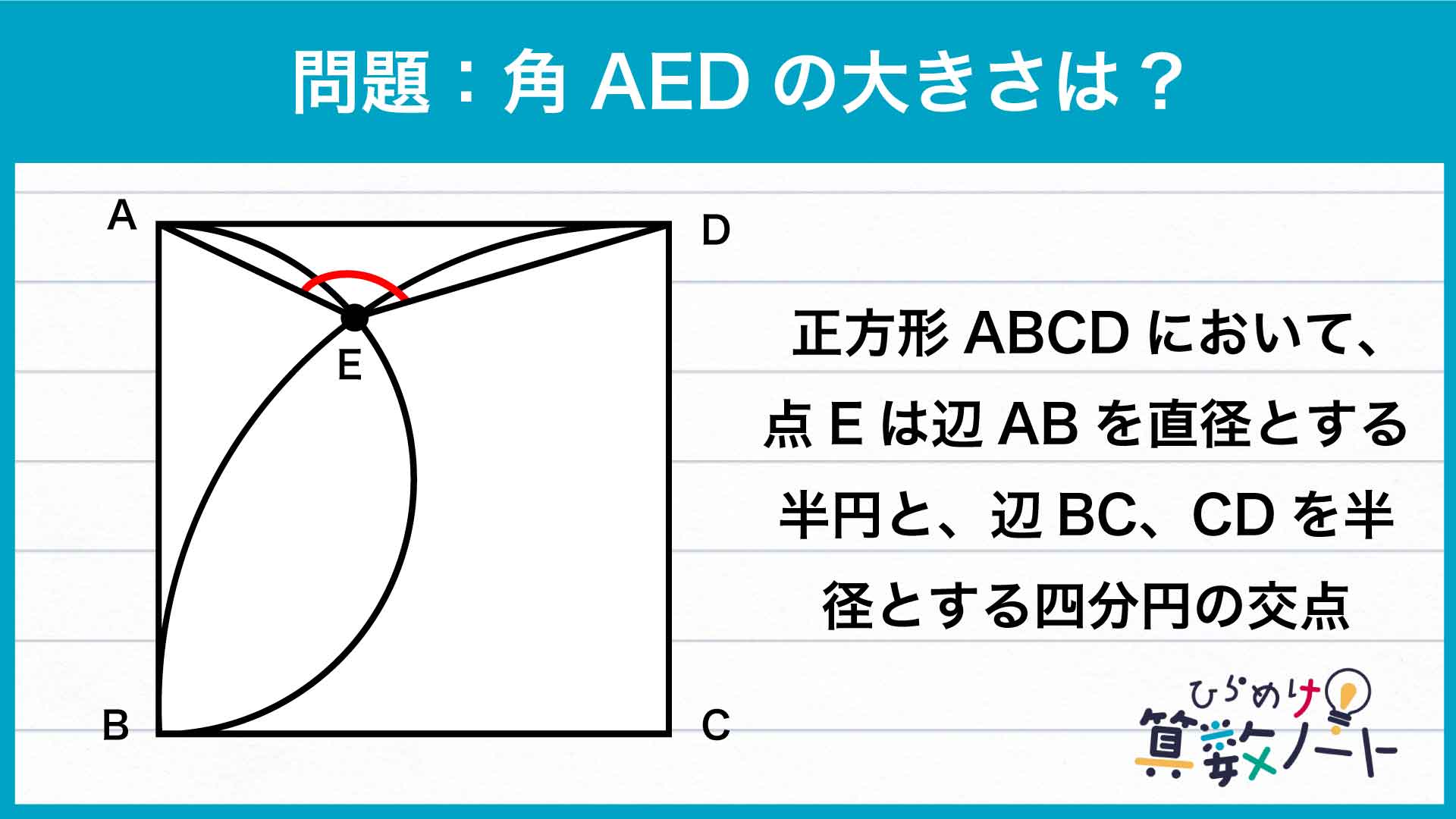
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引き、二等辺三角形を見つけることです。
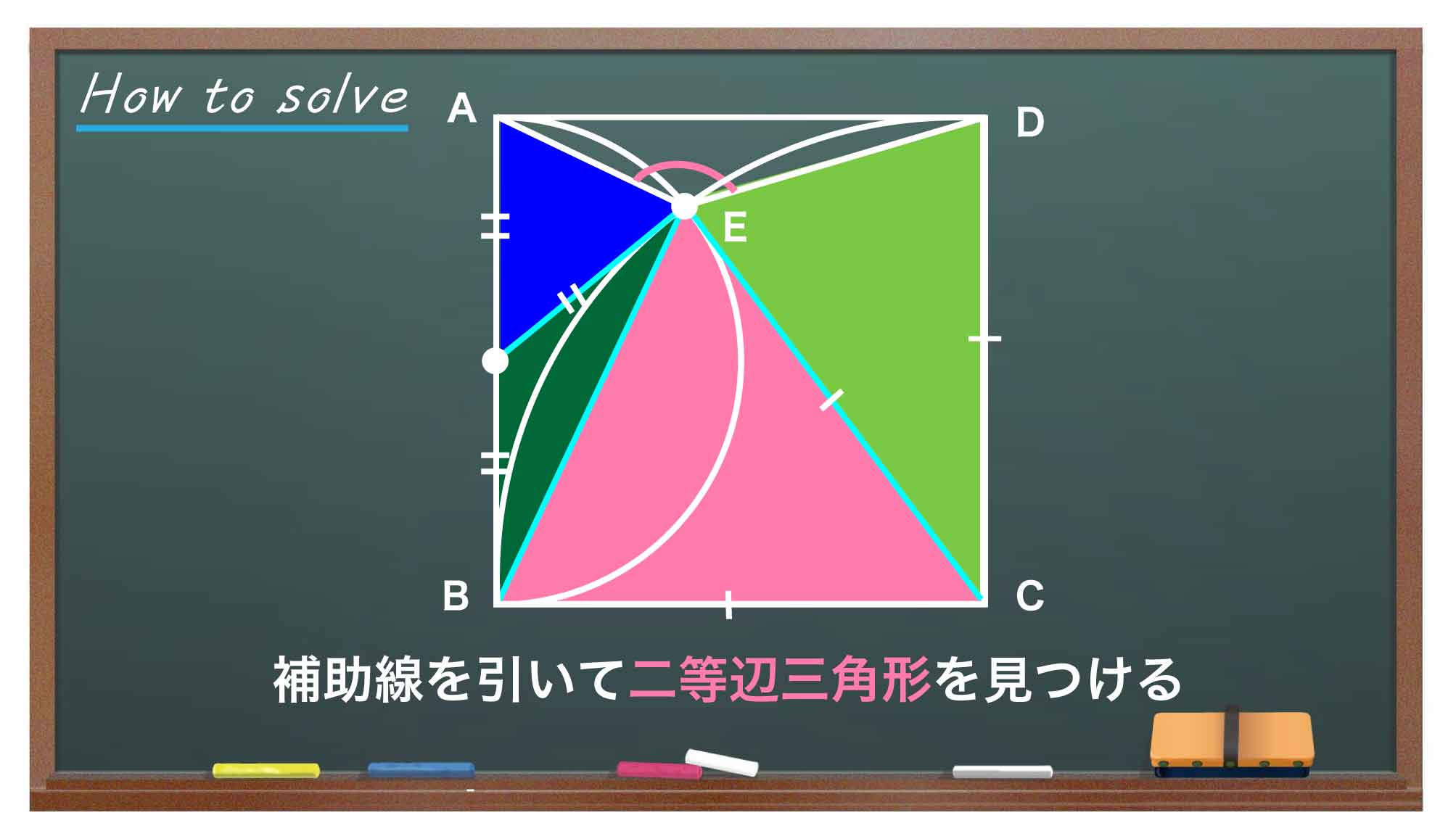
このポイントをもとに、解いていきましょう!
補助線を引く
まずは、点Bと点Eを結ぶ補助線を引きます。
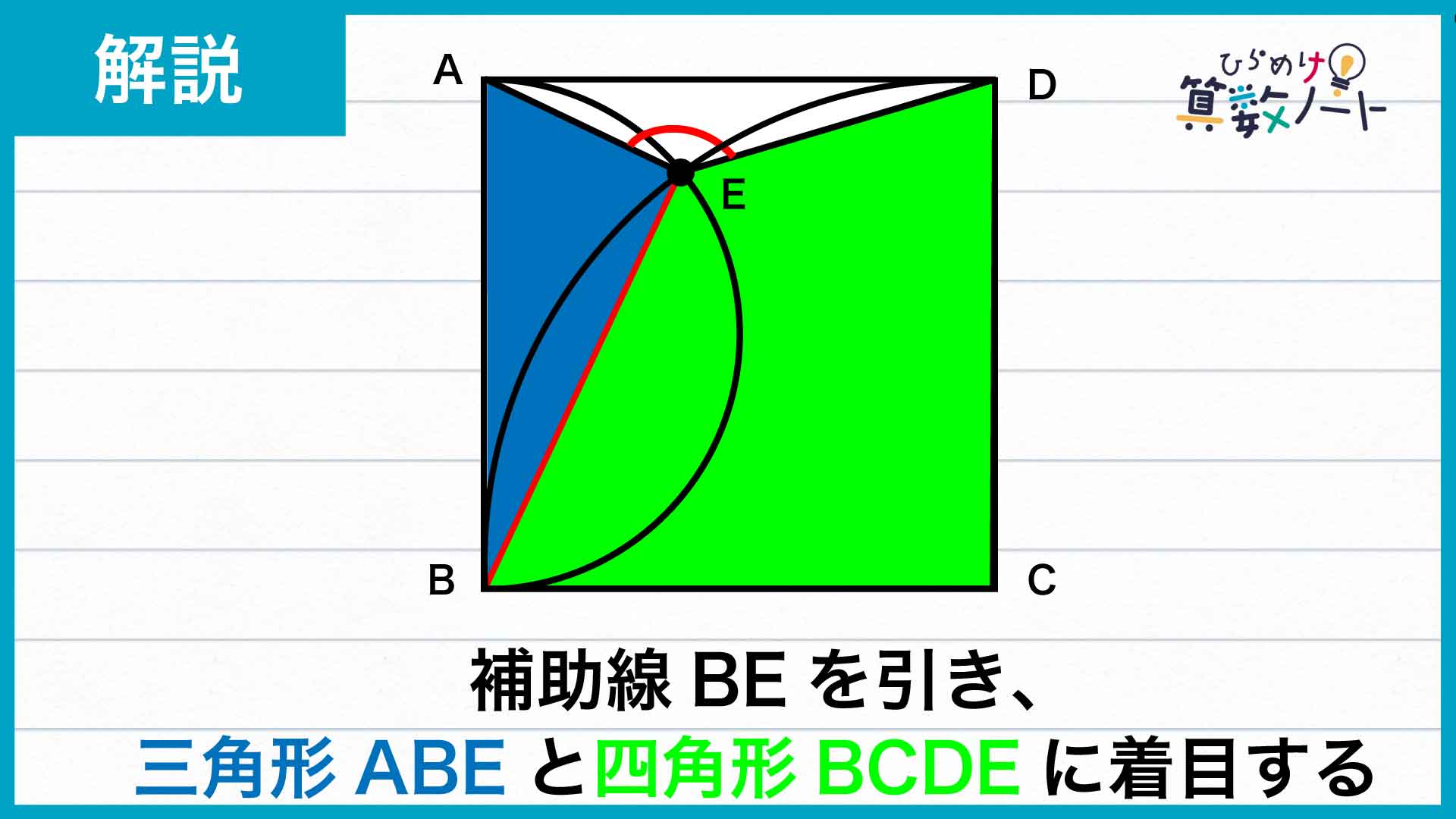
角AEB、角DEBの大きさがわかれば角AEDの大きさもわかります。角AEBの大きさを求めるために三角形ABEに、角DEBの大きさを求めるために四角形BCDEに着目しましょう。
角AEBを求める
三角形ABEはどの角の角度もわかっていません。そこで、辺ABの中点をFとして、補助線EFを引きます。
AF、BF、EFはいずれも辺ABを直径とする半円の半径なので、三角形AFE、三角形EFBは二等辺三角形であることがわかります。
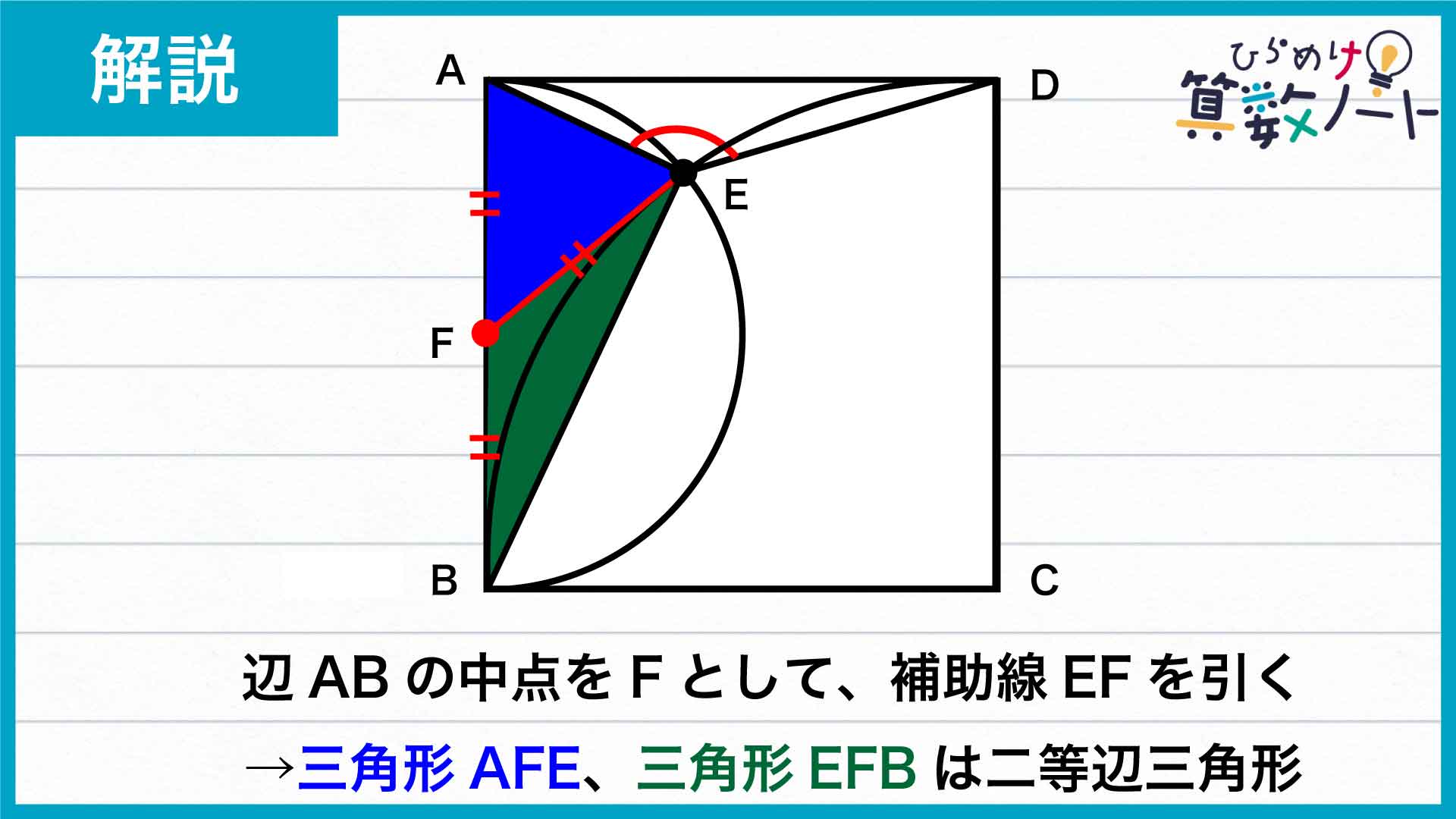
三角形AFEは、AF=EFの二等辺三角形であることから、角EAF=角AEFです。この角の大きさをaとおきます。
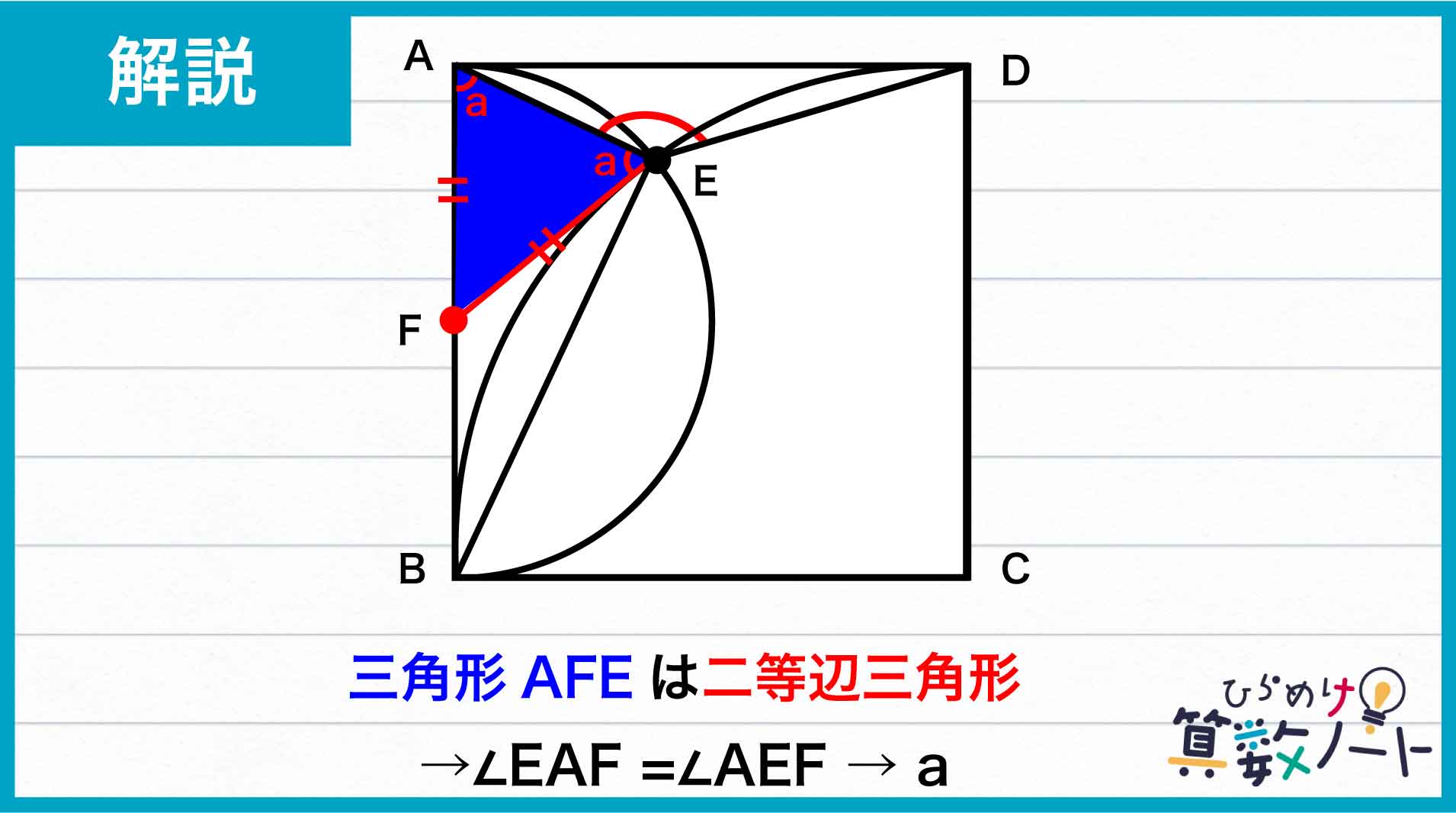
また、三角形EFBはEF=BFの二等辺三角形であることから、角BEF=角EBFで、この角の大きさをbとおきます。
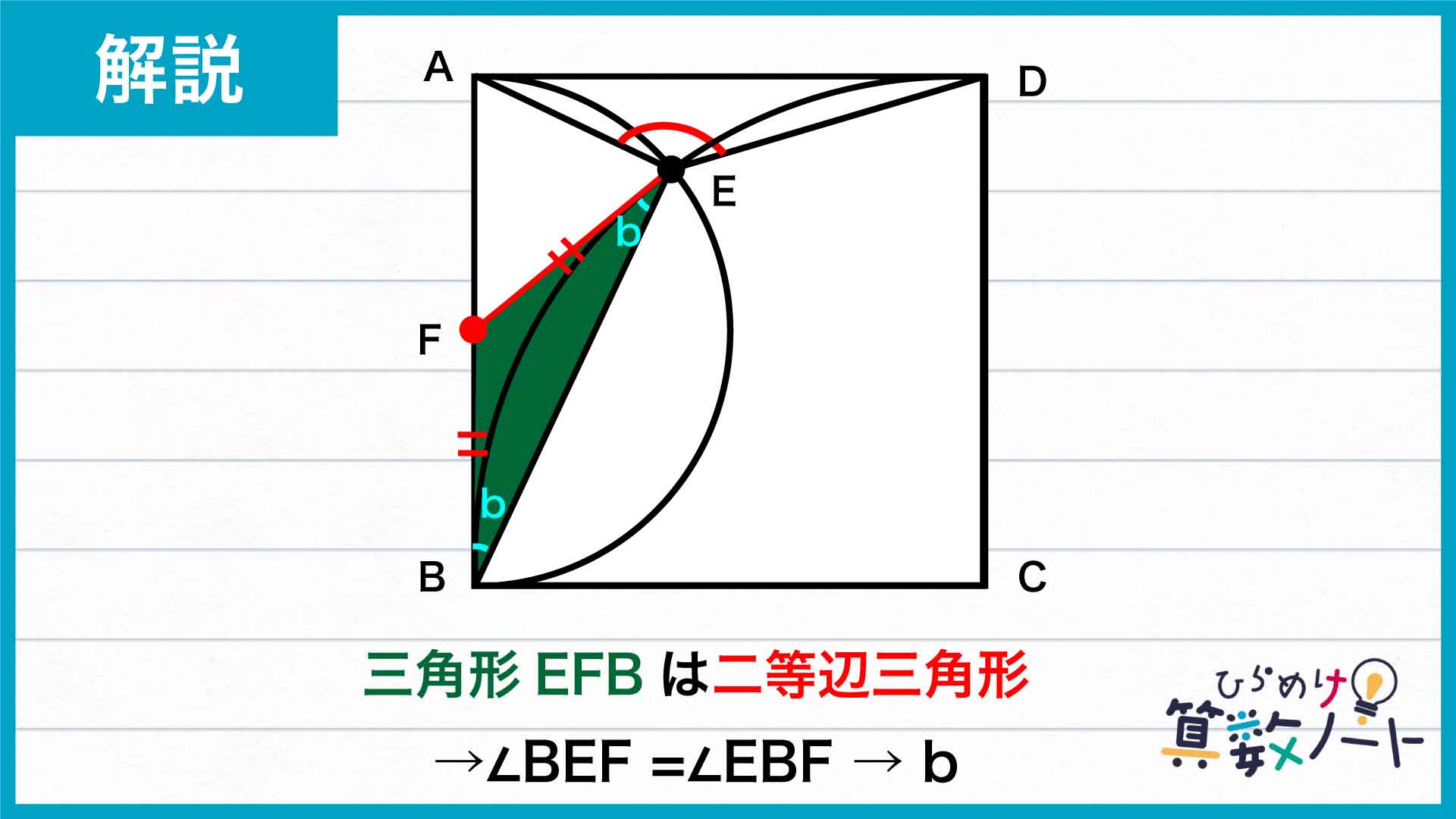
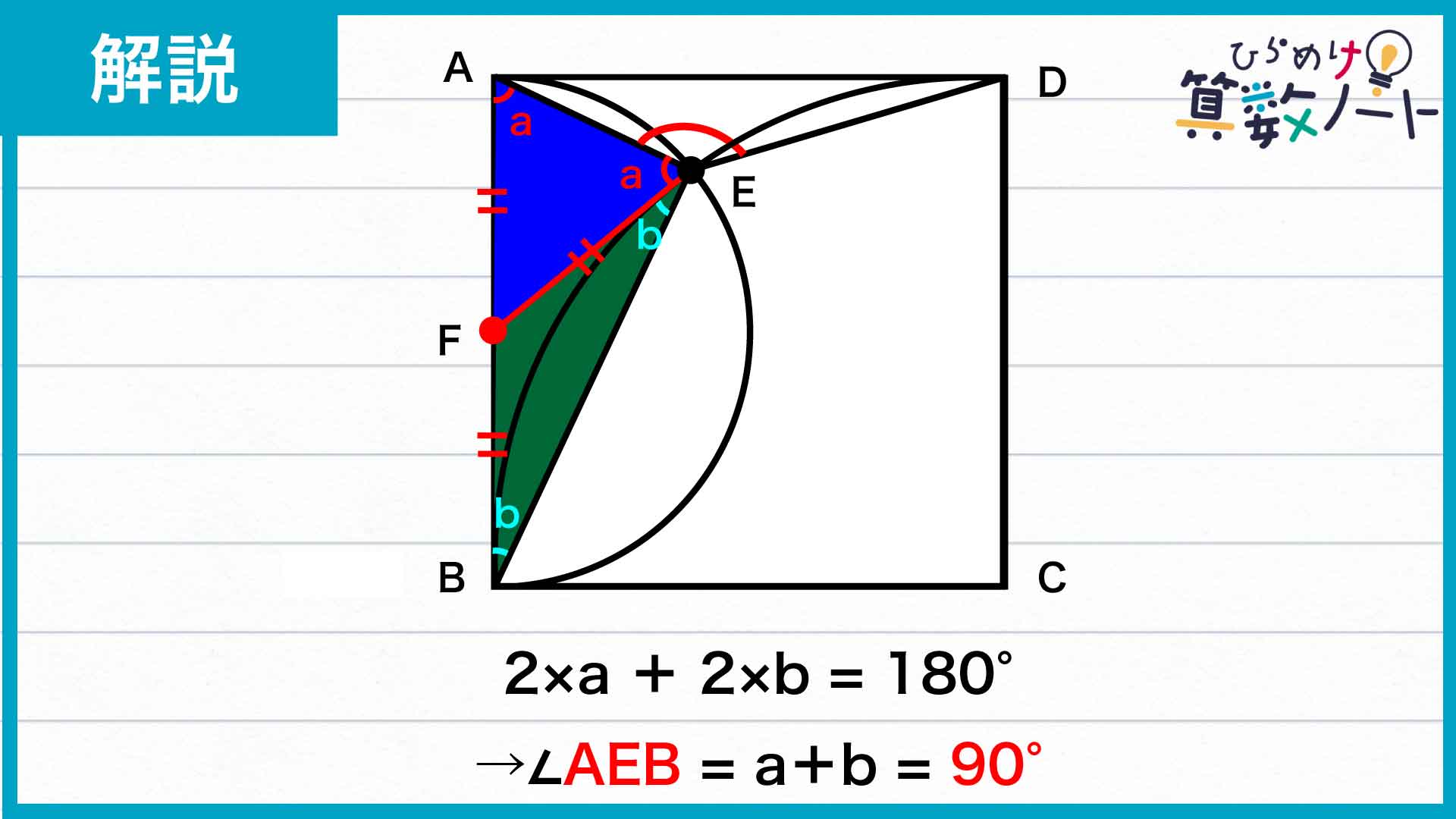
三角形ABEに着目すると、内角の和は、角ABE+角BEA+角EAB=b+(a+b)+a=2×a+2×bとなります。
三角形の内角の和は180度であり、2×a+2×b=180度であることから、a+b=180÷2=90度であることがわかります。
したがって、角AEB=a+b=90度です。
角BEDを求める
角BEDの大きさを求めるために、まずは補助線CEを引きます。
CB、CE、CDはいずれも四分円の半径なので、三角形EBC、三角形ECDは二等辺三角形です。
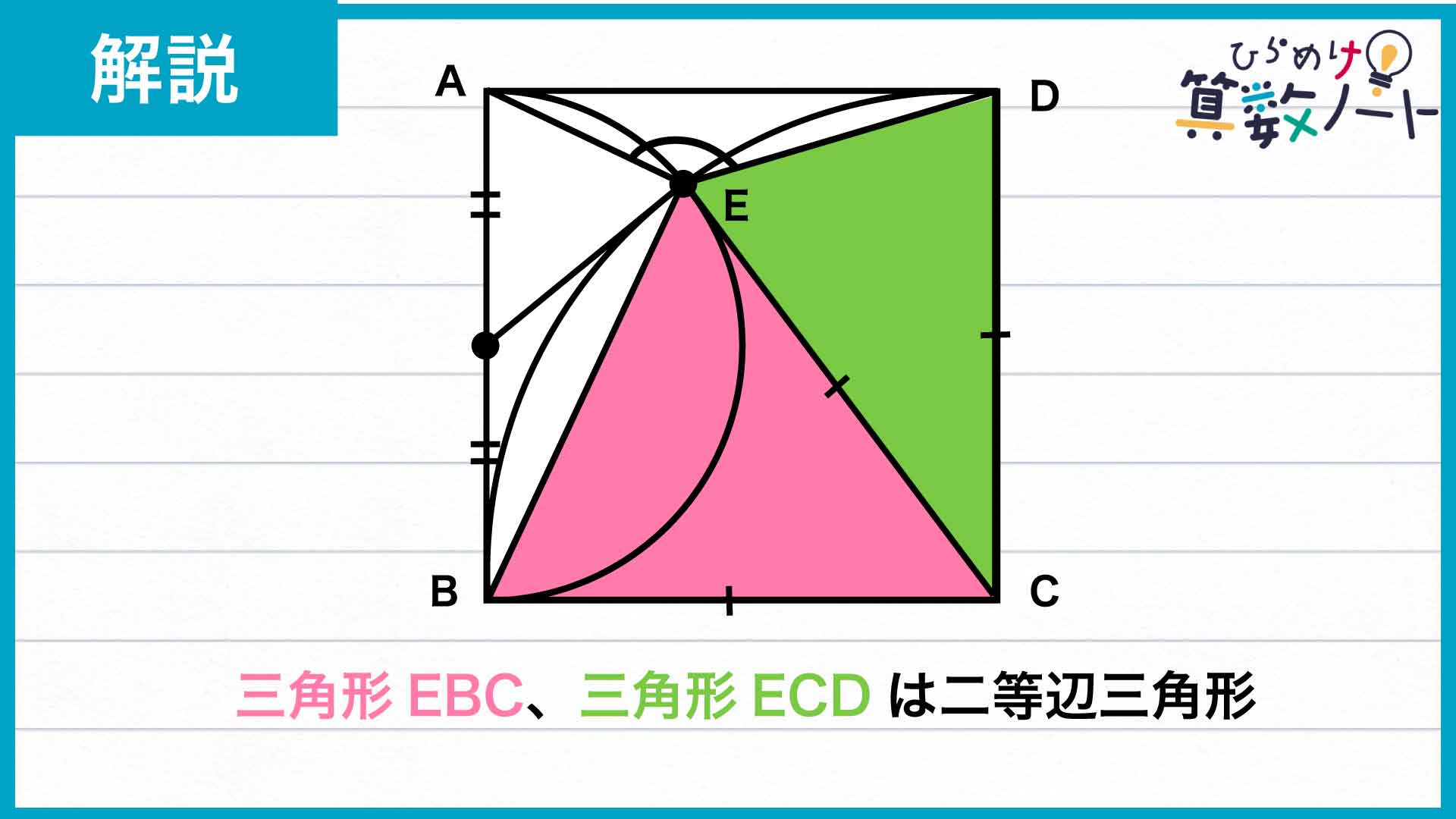
三角形EBCは、CB=CEの二等辺三角形であることから、角EBC=角BECです。この角の大きさをcとおきます。
また、三角形ECDはCE=CDの二等辺三角形であることから、角DEC=角EDCで、この角の大きさをdとおきます。
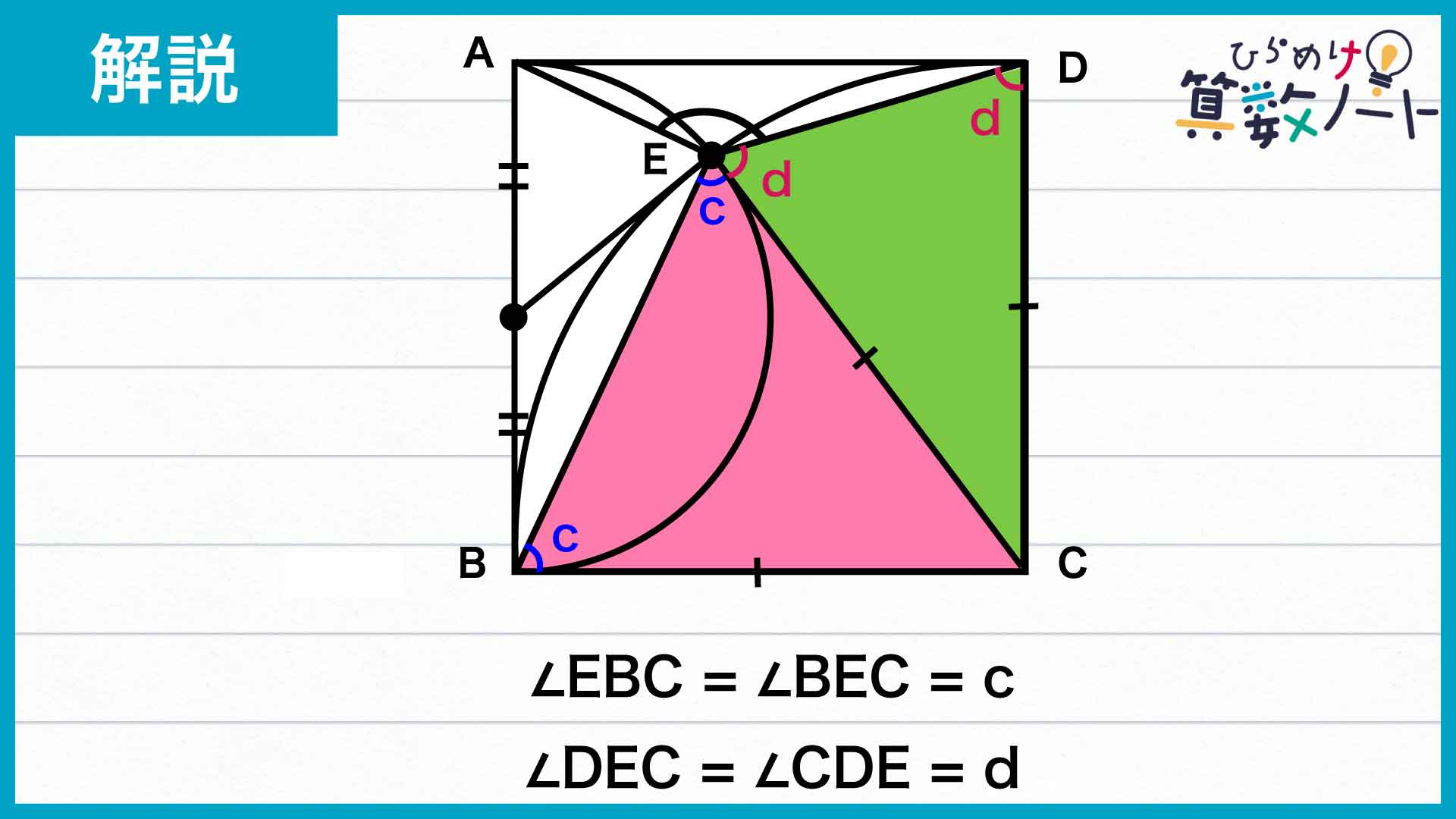
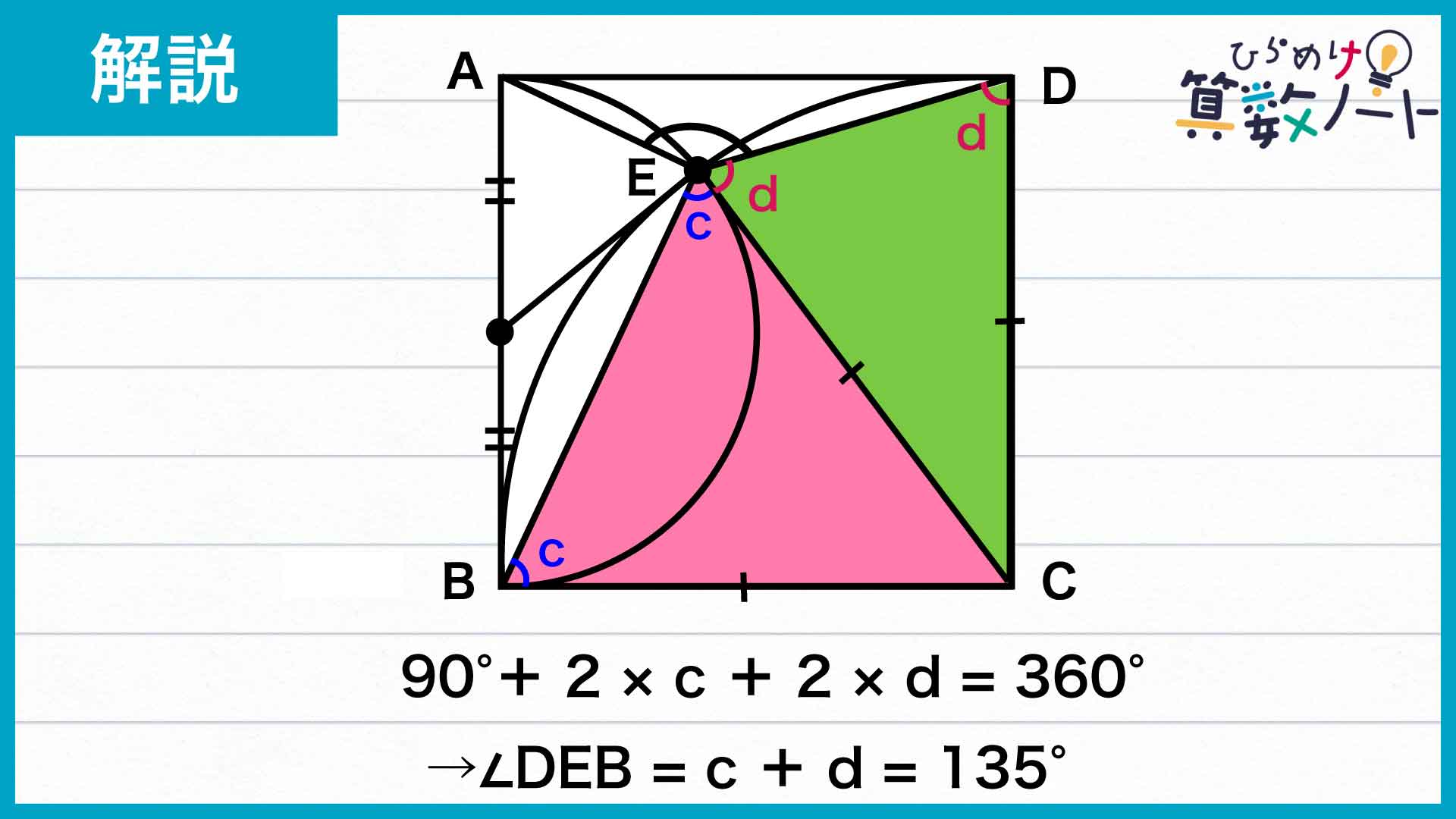
四角形BCDEの内角の和をcとdで表すと、角BCD+角CDE+角DEB+角EBC=90+d+(c+d)+c=90+2×c+2×dとなります。
四角形BCDEの内角の和は360度であることから、c+d=(360-90)÷2=135度であることがわかります。
したがって、角DEB=c+d=135度です。
あと一歩!
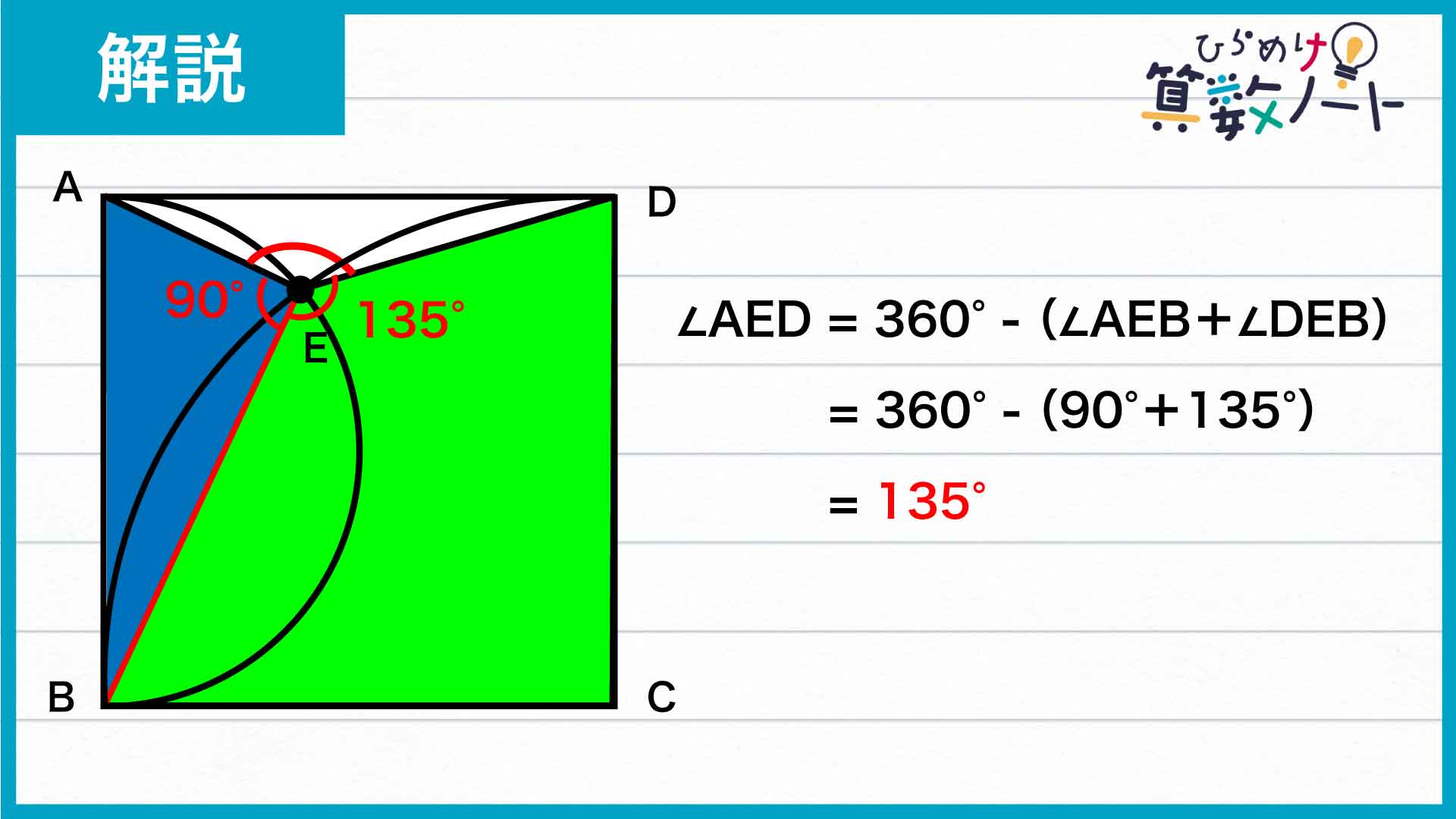
角AEBが90度、角DEBが135度であることがわかりました。
したがって、求めたい角AEDの大きさは、360-(角AEB+角DEB)=360-(90+135)=135度となります。
答え:135度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)











.jpg)







