小学5年生で解ける「面積を求める」問題に挑戦！あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

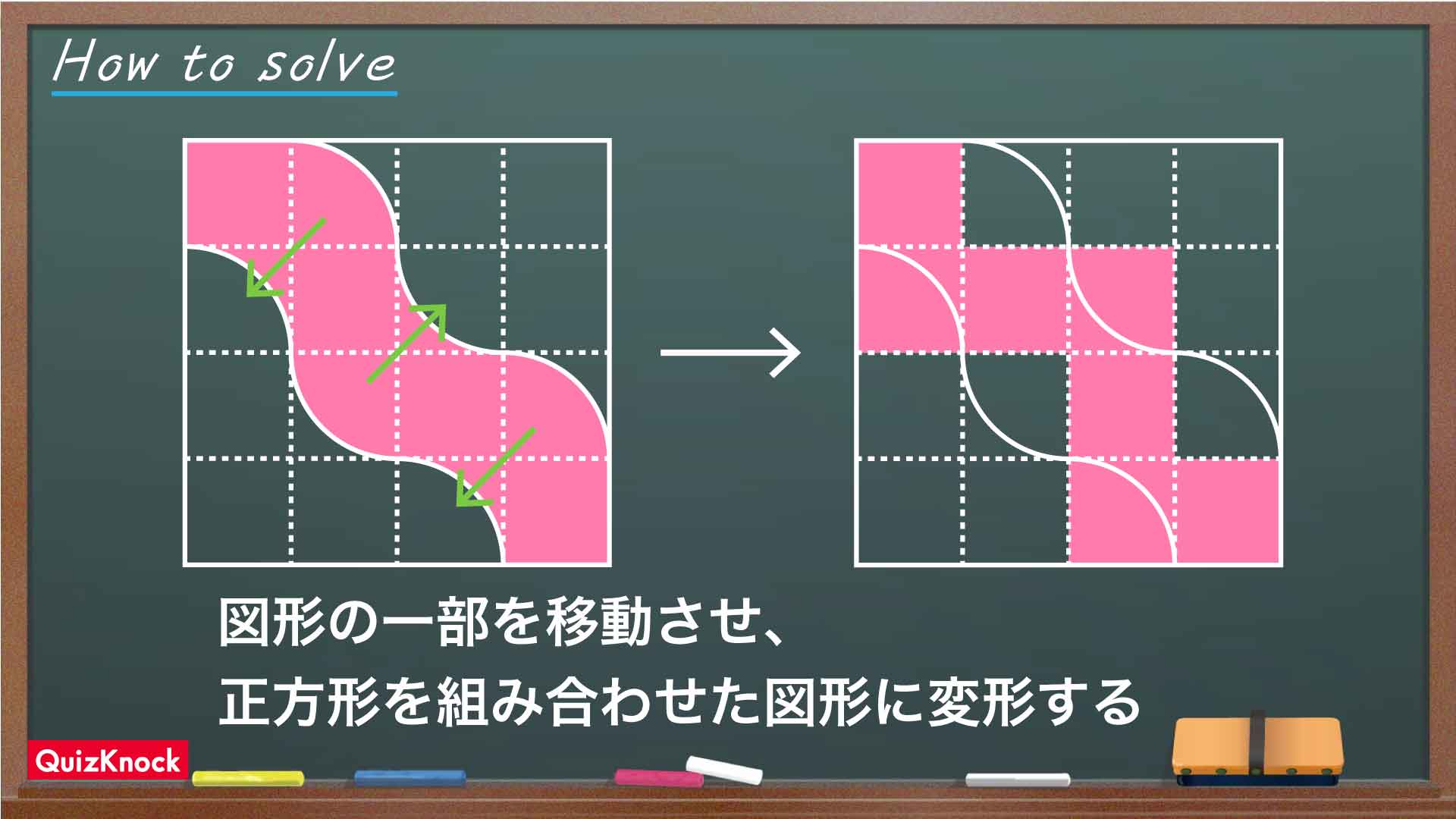
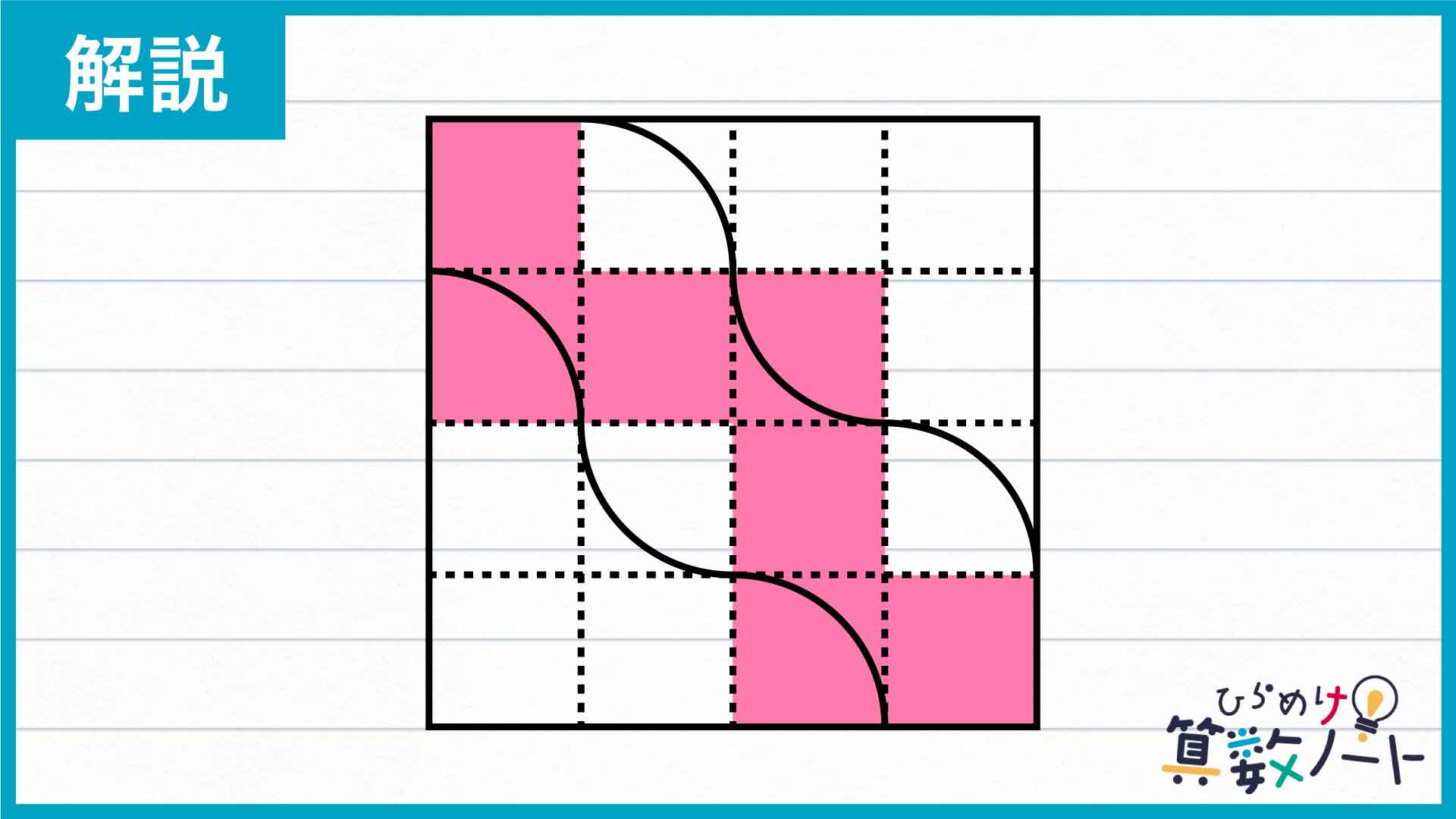
今回の解き方をまとめた図がこちらです。

今回のポイントは、「図形の形を見極め、一部を移動させて面積を求めやすい形をつくる」ことです。

このポイントをもとに、問題を攻略していきましょう！

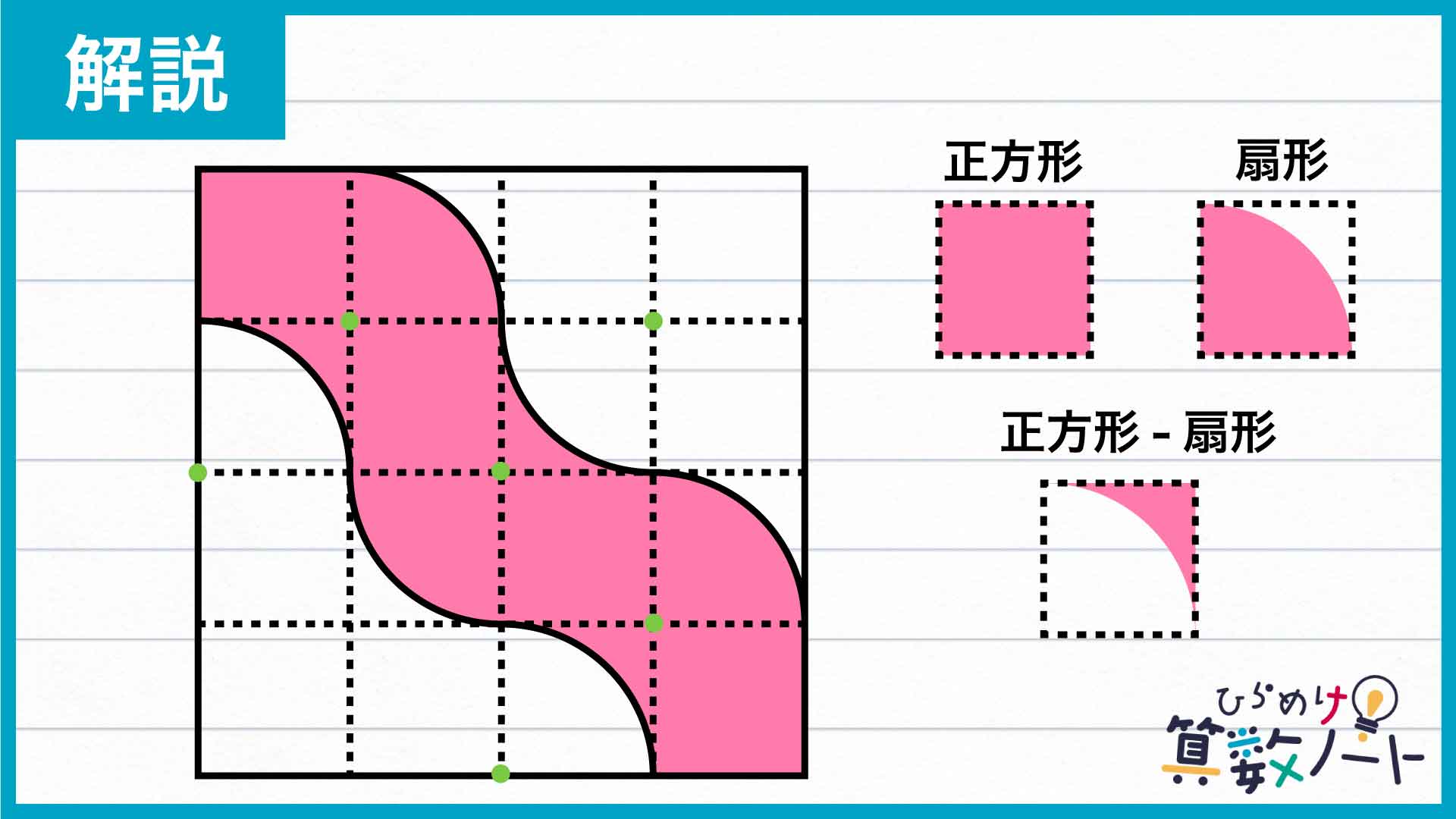
図形の構成を観察する

16等分したそれぞれの正方形の中にある色が塗られた図形の形を見ると、色が塗られた図形は「正方形」「扇形」「正方形から扇形を引いた図形」で構成されていることがわかります。

図形を移動して正方形を作る

「扇形」と「正方形から扇形を引いた図形」は、どちらも3つずつあります。

したがって、「扇形」を「正方形から扇形を引いた図形」のある場所に移動させると、新たに3つの正方形を作ることができます。

小さな正方形の面積を求める

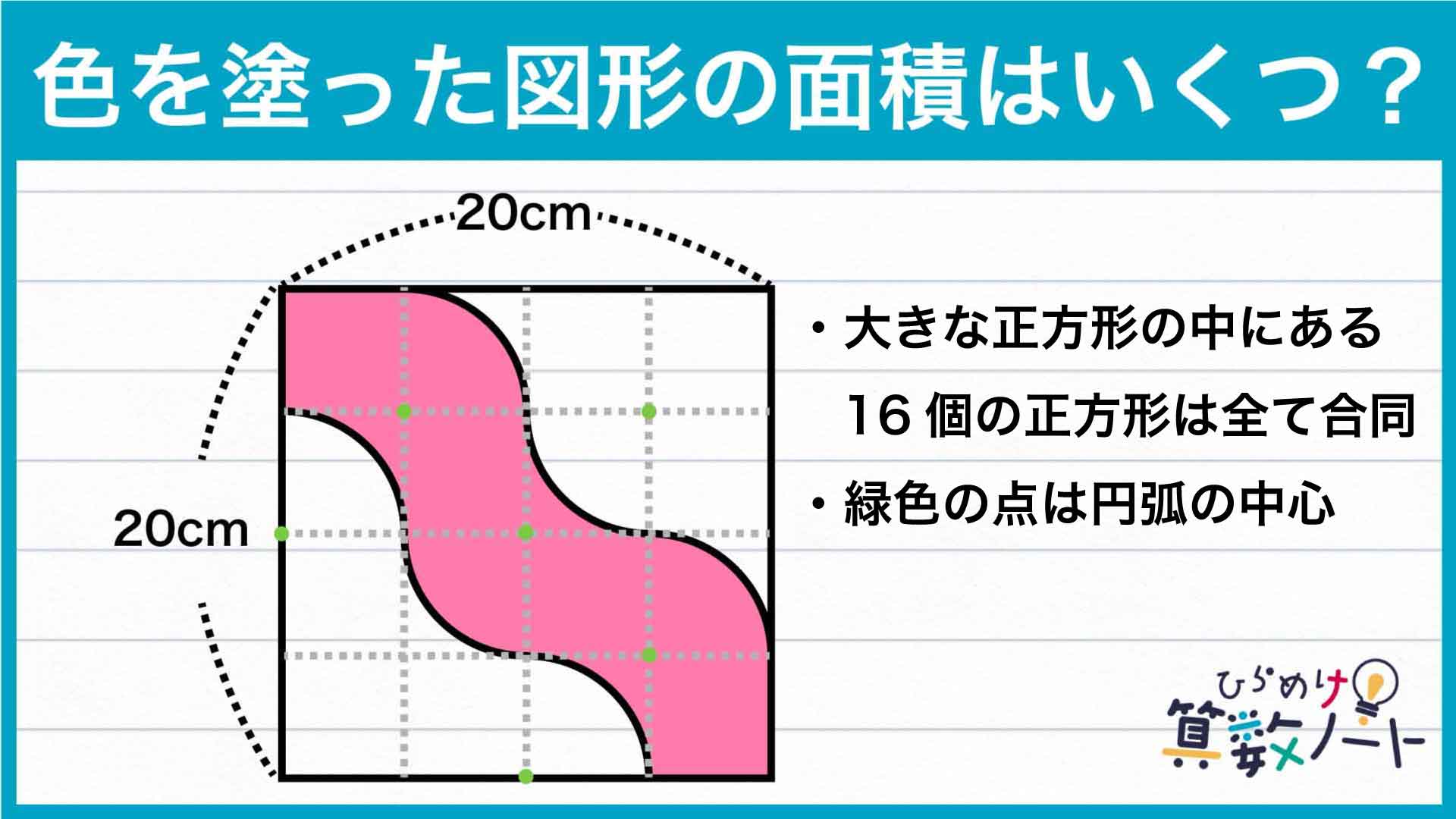
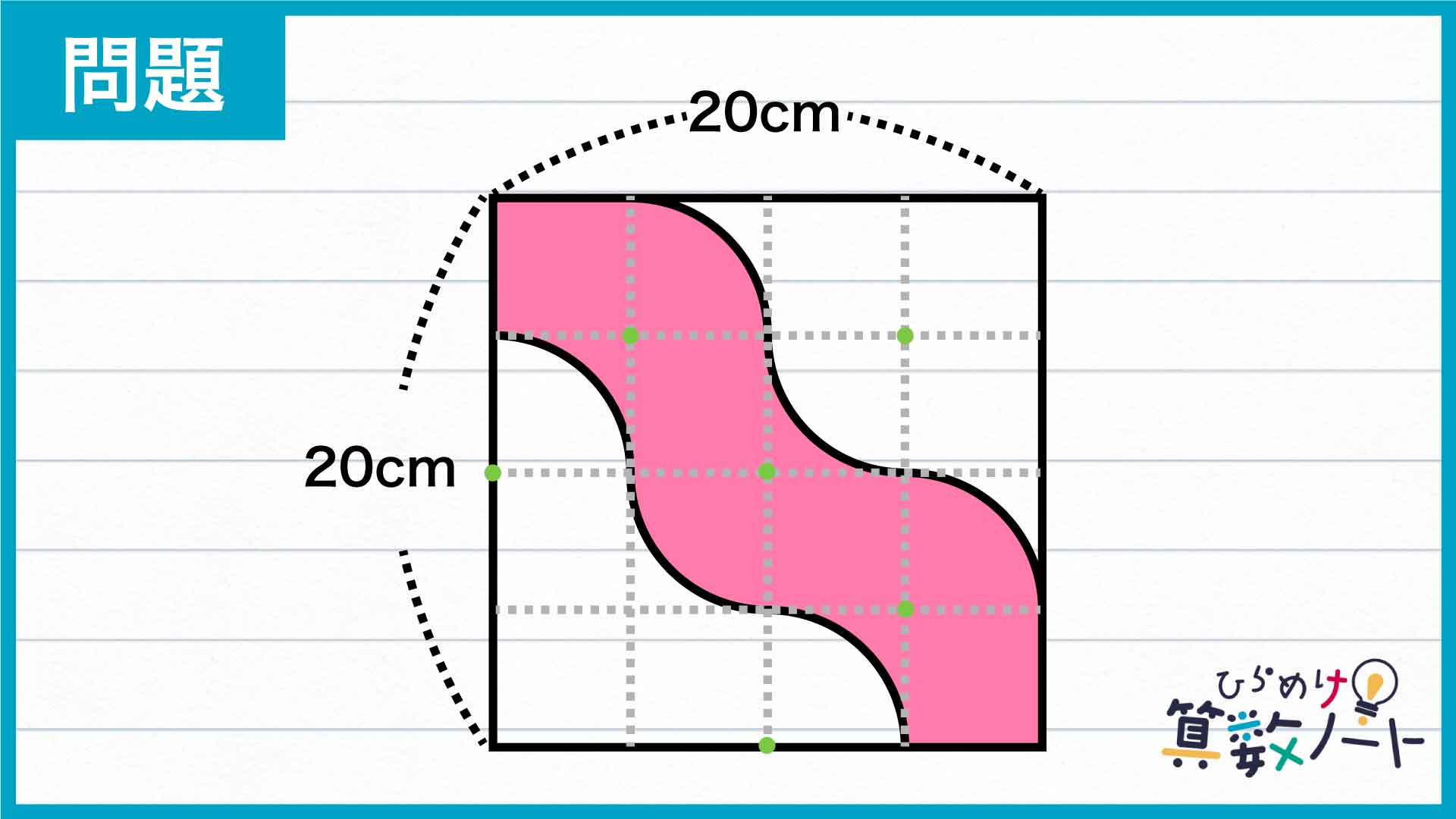
大きな正方形の1辺の長さは20cmなので、16等分した正方形の1辺の長さは20÷4=5cmです。

したがって、16等分した正方形ひとつ分の面積は5×5=25cm²となります。

色を塗った図形の面積を求める

一部の図形を移動し、色が塗られた図形は16等分した正方形7つ分であることがわかりました。

したがって、色が塗られた部分の面積は、25×7=175cm²となります。

答え：175cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】