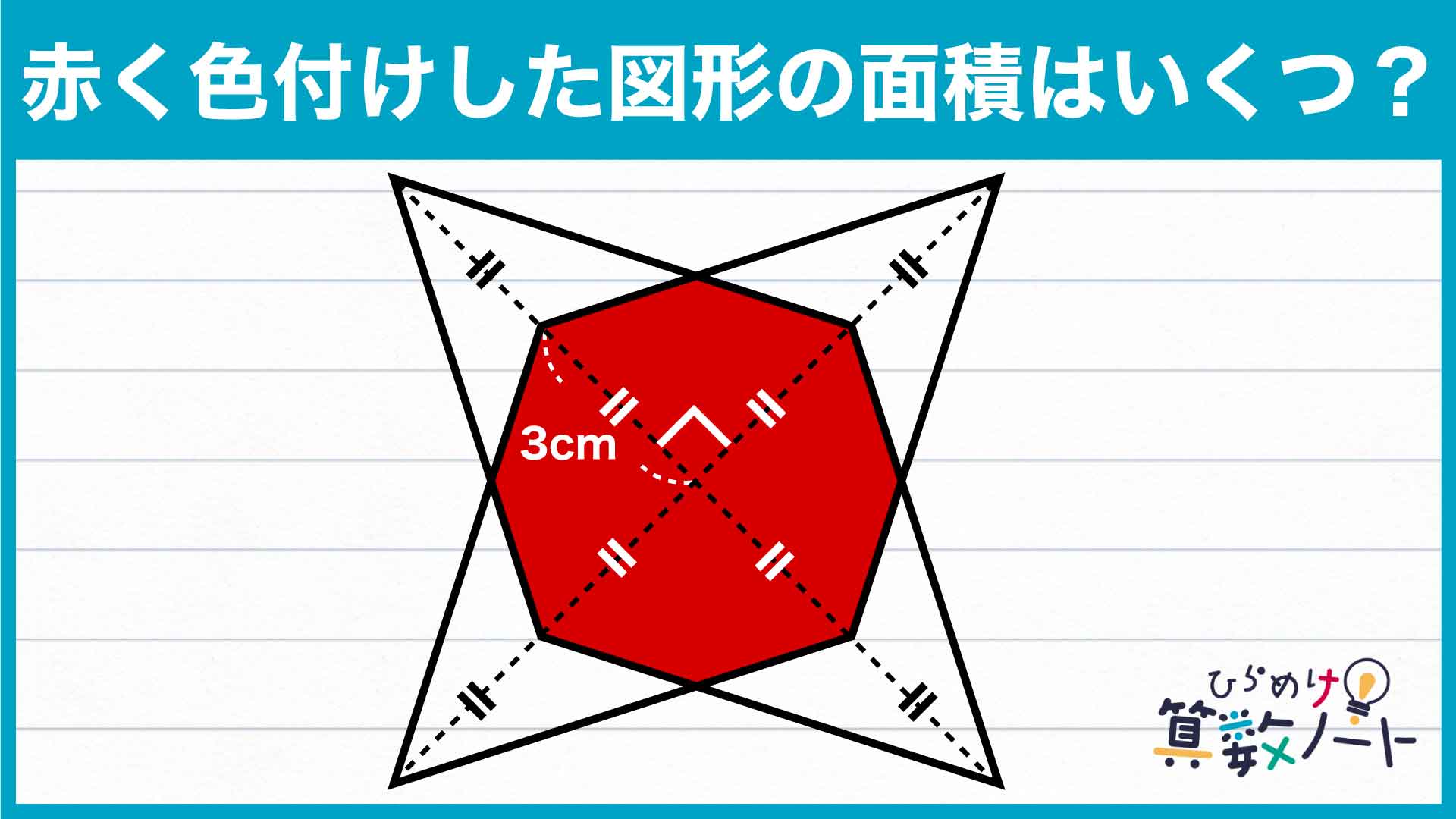
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
整理すると、
- 補助線をひき、八角形を分割する。
- 底辺が同じ長さの三角形は面積が等しくなることを利用する。
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
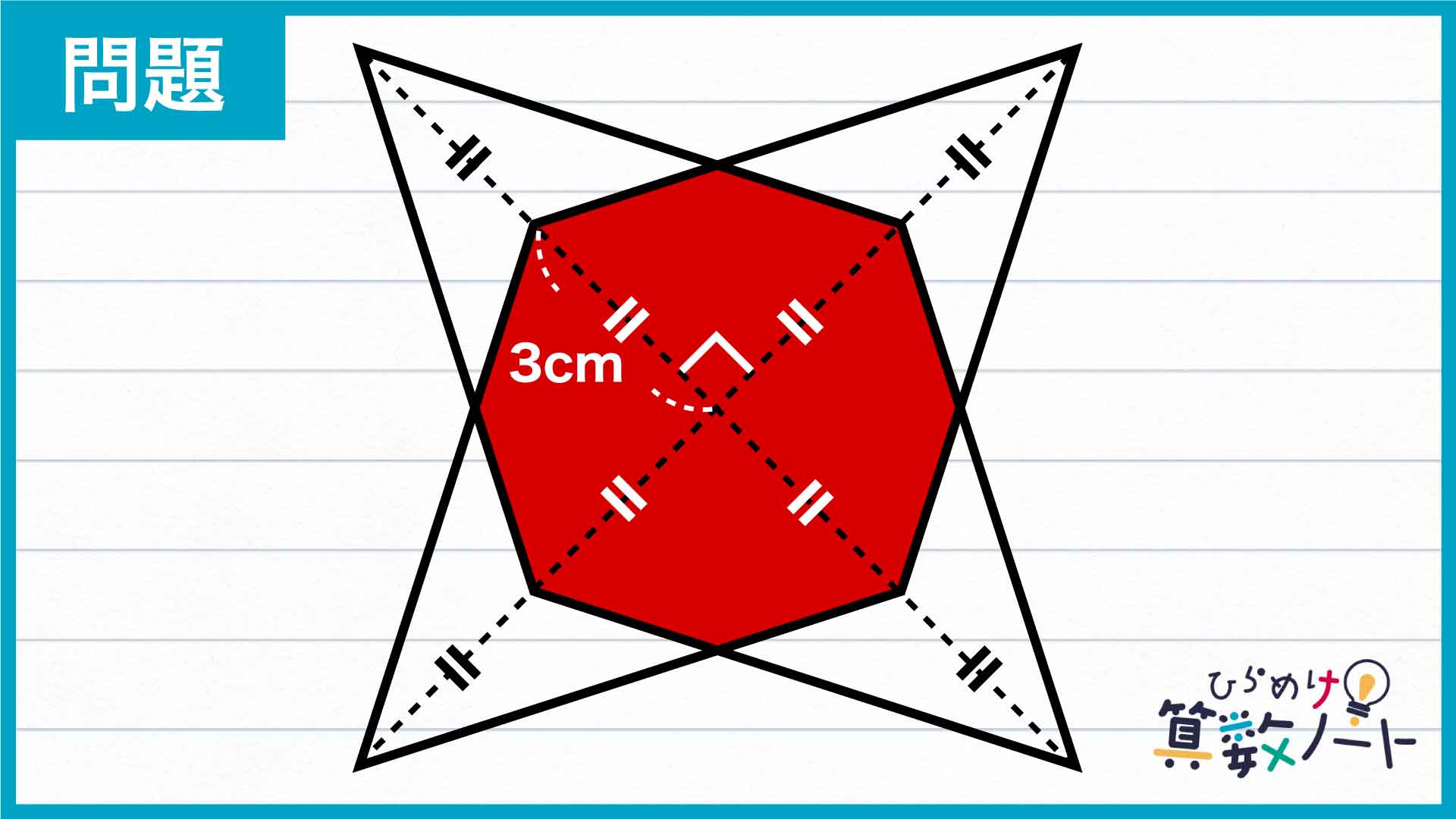
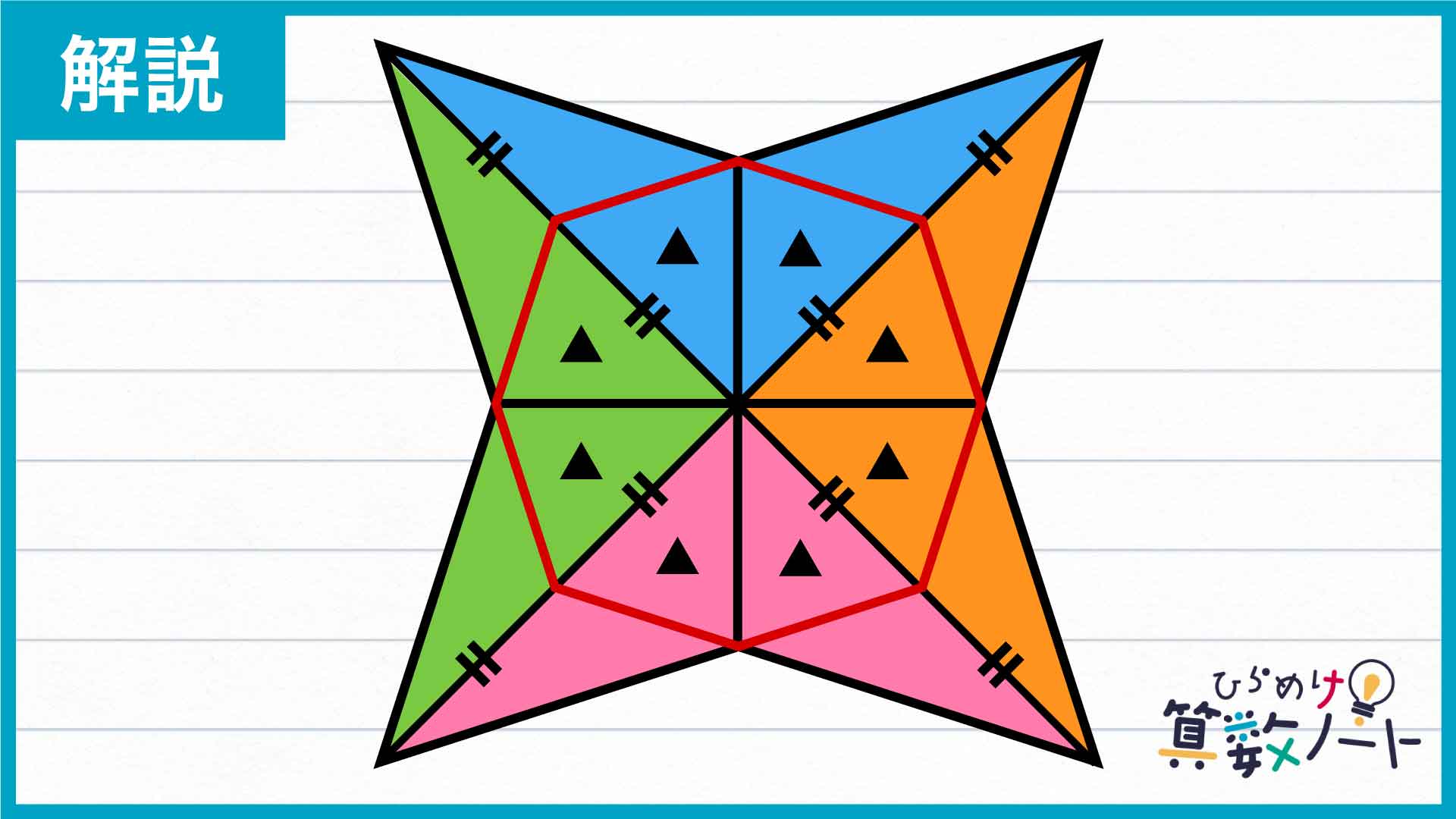
八角形を8つに分割する
下の図のように、八角形を8つの部分に分割します。
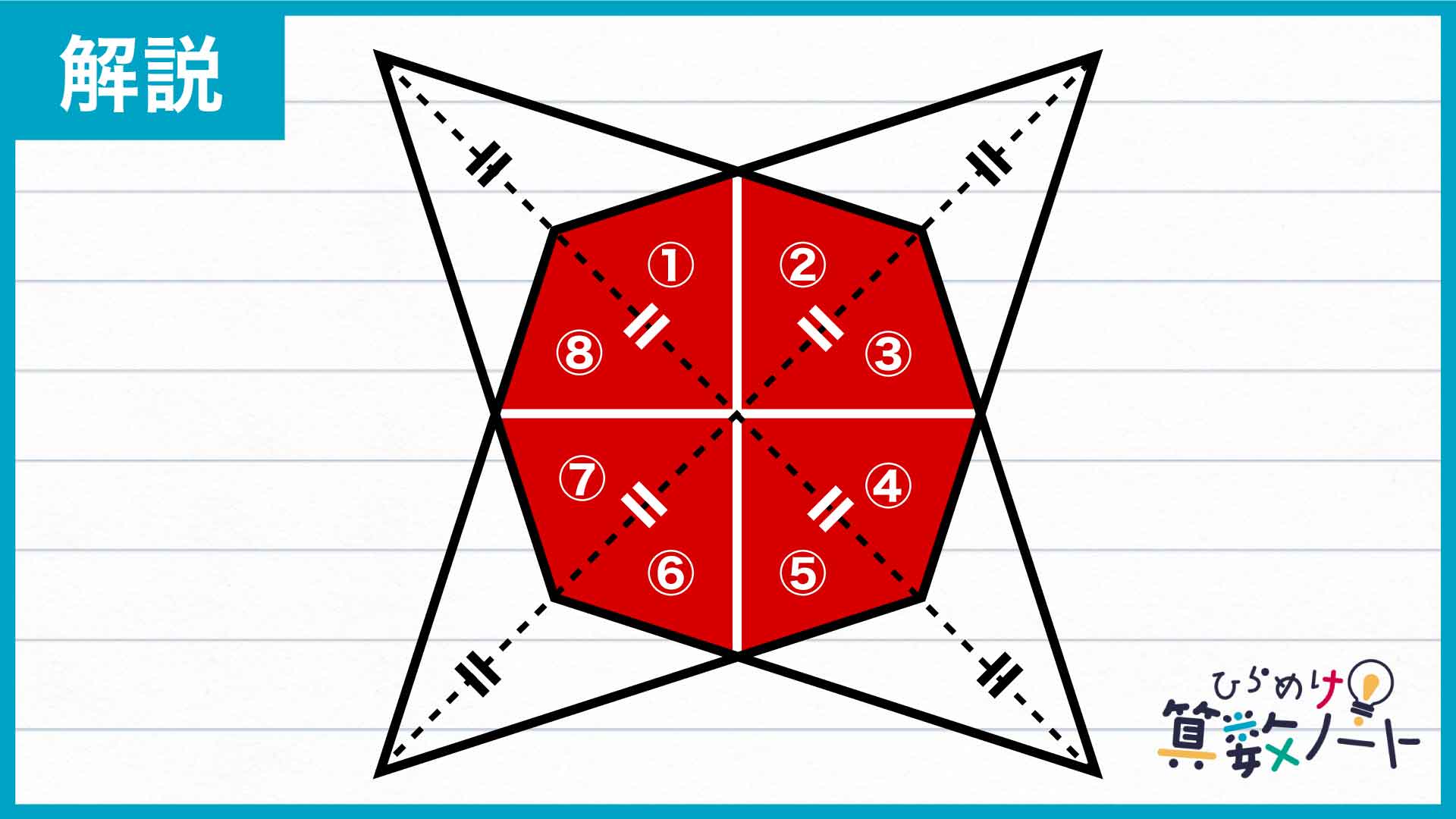
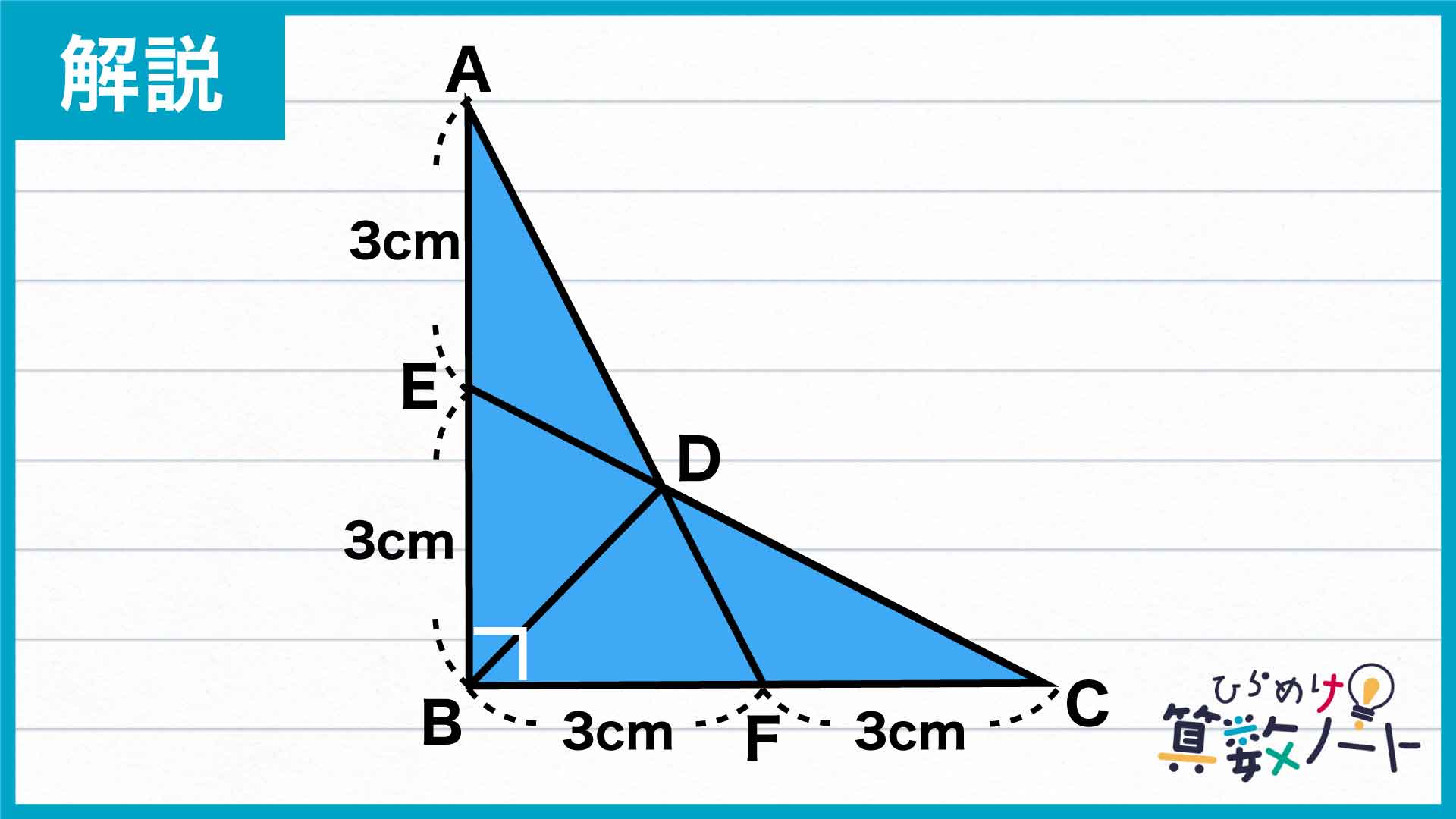
ここで、下の図の青い部分に注目しましょう。
点Aから点Fまでの点を下の図のように振っておきます。
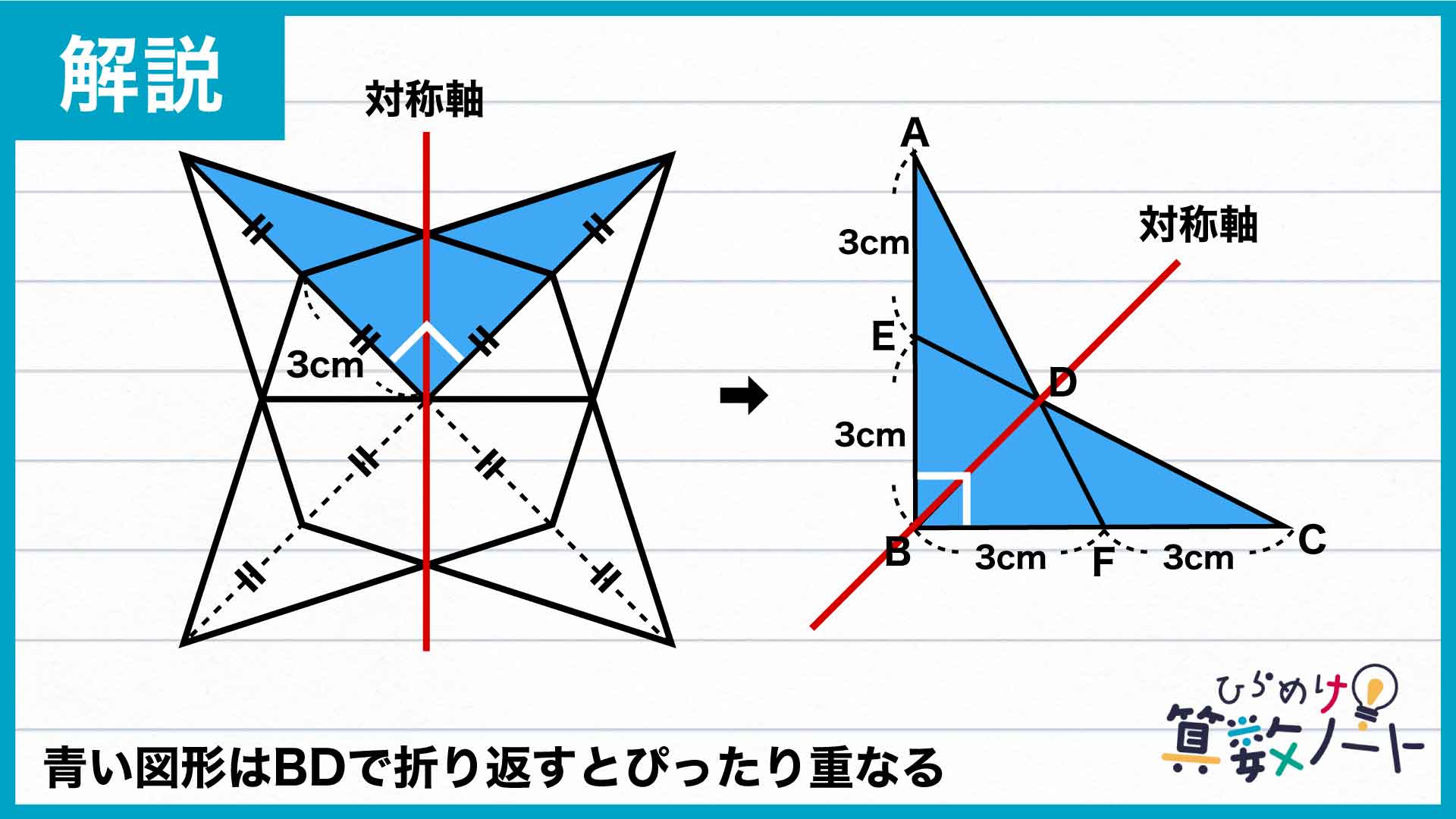
設問の図形は、同じ大きさのひし形2つを90度回転させて重ねたものなので、図形全体を見ると線対称になっています。したがって、辺BDを折り目にして図形ABCDを折り返すと、ちょうどぴったり重なることがわかります。
以上より、三角形BDEと三角形BDFは合同な図形になり、面積も同じになることがわかります。
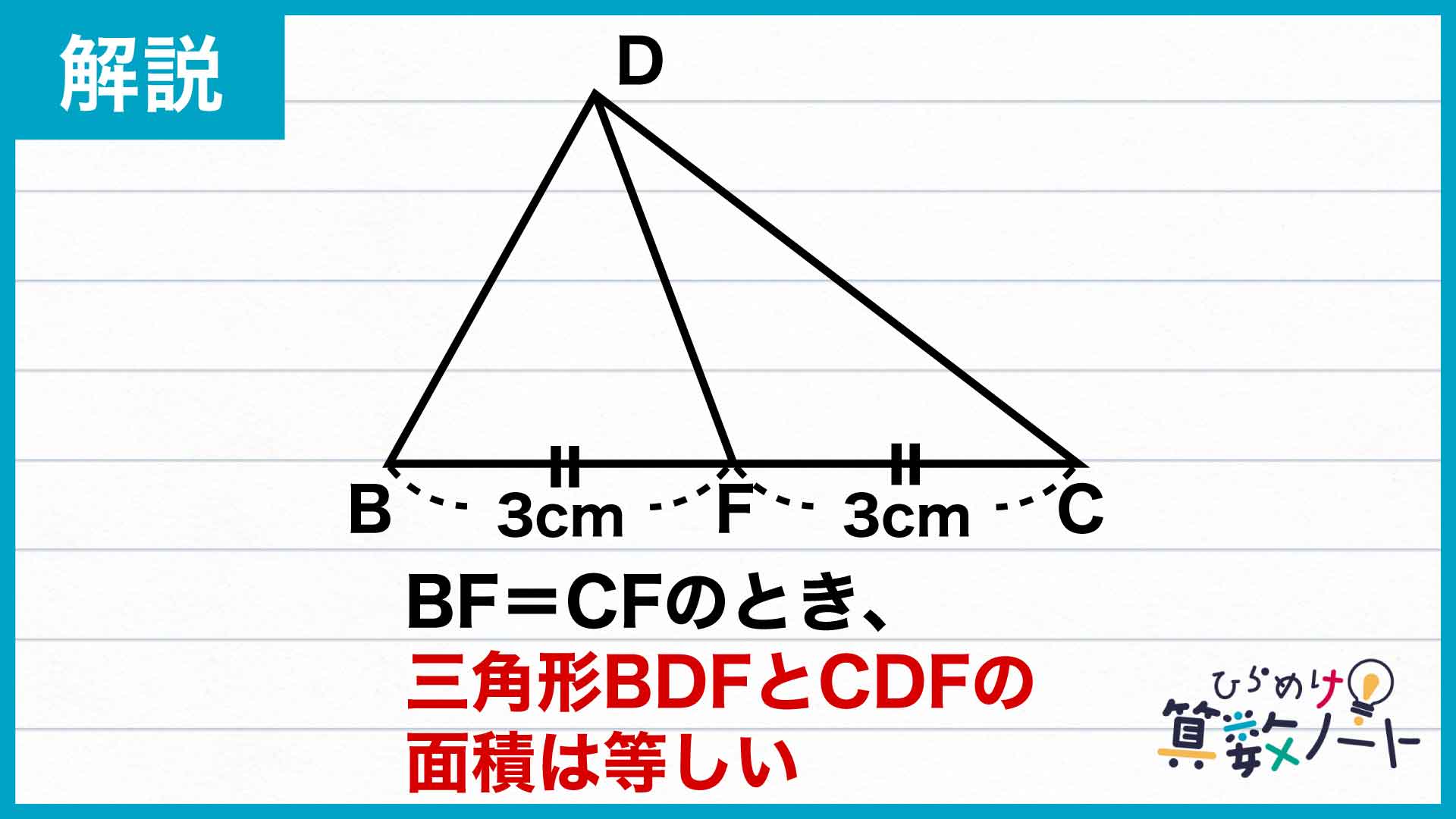
次に、三角形BDFと三角形CDFに注目しましょう。ここで、次の性質を使います。
BFの長さとCFの長さは同じなので、上の性質を用いると、三角形BDFと三角形CDFの面積は同じになります。
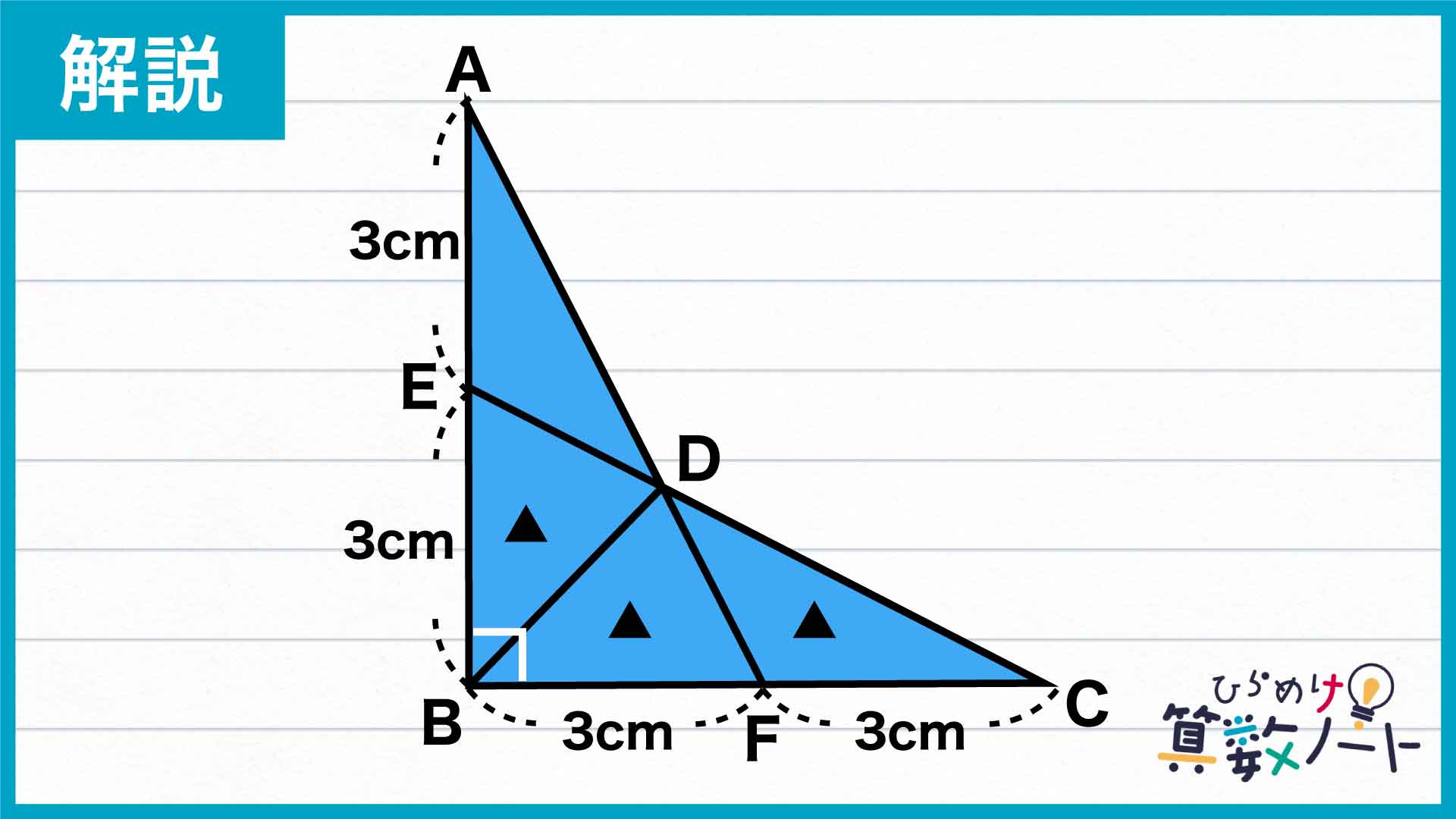
こうして、三角形BDE、三角形BDF、三角形CDFの面積は全て同じになることがわかります。
▲の印をつけた三角形1個分の面積を求める
三角形BDE、三角形BDF、三角形CDFの面積を▲としましょう。
(三角形BDEの面積)+(三角形BDFの面積)+(三角形CDFの面積)=(三角形EBCの面積)です。また、三角形EBCは、角EBCの大きさが90度の直角三角形であり、その面積は3×6÷2=9㎠です。以上より、3×▲=9cm2となるので、▲=3cm2であることがわかります。
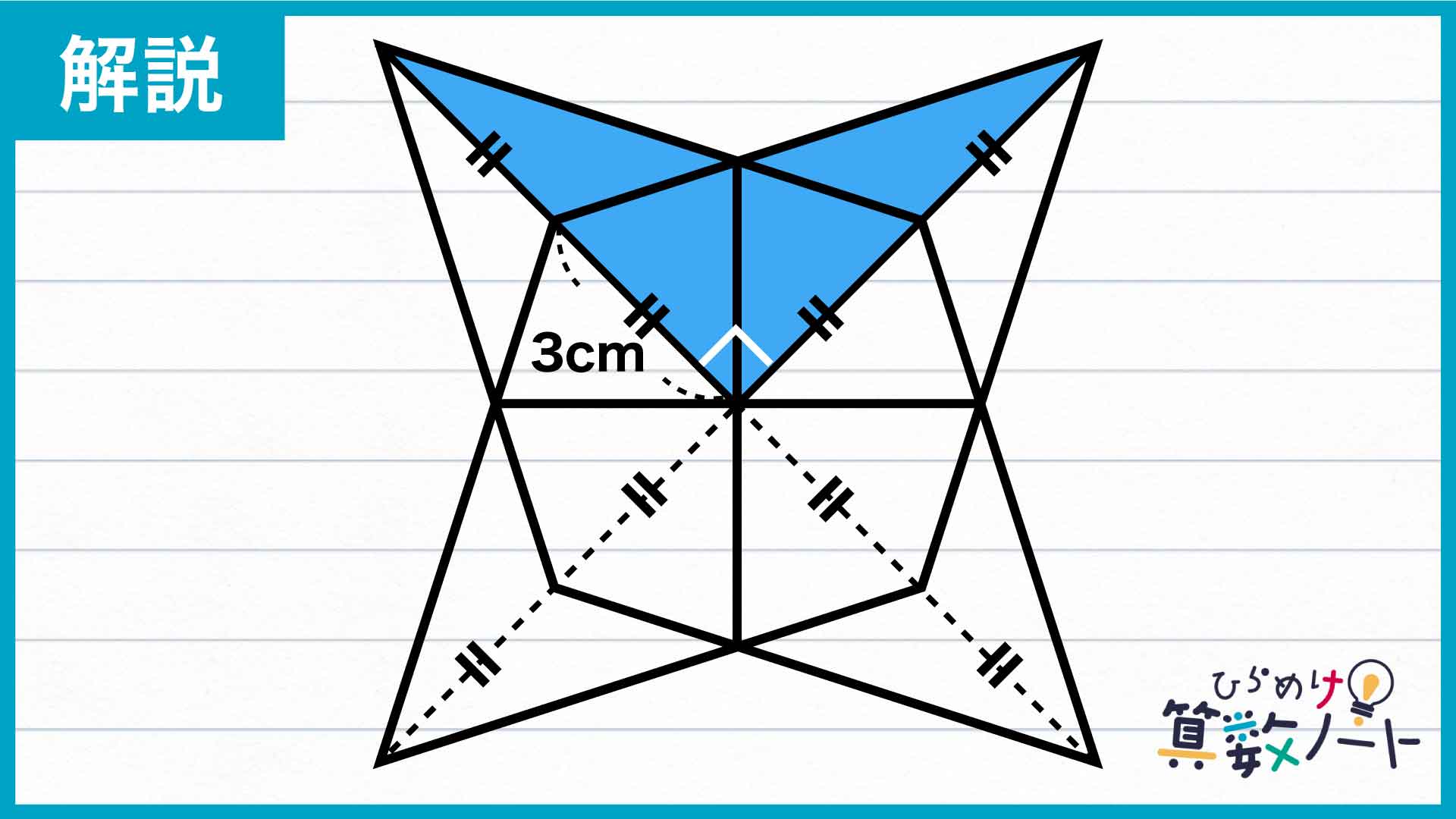
色のついた部分の面積を求める
では、最後に設問の赤い八角形の面積を計算しましょう。図形の対称性から、上記の青い図形に対して行った操作を以下の図の緑、ピンク、オレンジ色の図形に対しても行うと、赤い八角形の面積は、▲の面積の8個分であることがわかります。
したがって、答えは3cm2×8=24cm2となります。
答え:24cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】













.jpg)







.jpg)







